基于深度卷積神經網絡的點云三維目標識別方法研究

李豪杰，楊海清

(浙江工業大學 信息工程學院，杭州 310012)

0 引言

三維激光掃描技術被廣泛應用于自動駕駛[1]、建筑施工[2]以及遙感測繪等領域[3]，其通過三維激光掃描儀或者三維激光雷達等掃描設備來獲取被測物體空間和表面紋理等信息，具有分辨率高，采集速度快以及非接觸式等優點。三維掃描設備得到的是被測物體的三維點云信息，其抗干擾能力強，不受外界因素影響，從而更有利于目標識別與姿態估計[4]。然而，傳統基于三維點云數據的目標識別方法有著計算數據量大以及速度慢等問題[5]，因此，對基于激光點云數據的三維目標識別方法進行研究具有十分重要的現實意義。

近年來，學術界對基于點云數據的三維目標識別方法進行了很多相關研究。在以深度神經網絡為代表的深度學習還沒有興起之前，計算機視覺領域主要采用傳統的機器學習方法對點云目標進行分類和檢測，如支持向量機(SVM，support vector machine)[6]和決策樹(Decision Tree)[7]等。文獻[8]采用基于點云梯度的局部最優分割方法對激光雷達掃描的點云目標進行梯度分割以提取出障礙物輪廓，并根據障礙物三維點云數據特征，利用基于核的支持向量機有效完成了障礙物分類。然而，傳統機器學習算法的魯棒性能和泛化能力較差，無法滿足現實生活中復雜場景下應用的需要。因此，研究人員將研究重點轉向了對點云數據特性的挖據上，引入降維思想將三維點云轉化為深度圖，借助圖像中的關鍵點檢測方法提取點云特征點。文獻[9]利用三維激光雷達傳感器的隱式拓撲將三維點云目標映射到二維圖像上，并提出了一種基于深度直方圖的移動對象半自動分割方法和引入變分圖像修復方法來重建被物體遮擋的區域，實際三維激光雷達街道場景驗證了該算法的有效性。

隨著人工智能時代的到來，深度學習算法在目標識別任務中取得了廣泛的應用和突破性的進展[10]。典型的卷積結構需要高度規則的輸入數據格式，所以無序散亂點云數據首先需要轉換為常規的三維體素網格或圖像集合[11]，這會導致數據不必要的損失，且帶來額外的工作量。針對上述問題，文獻[12]提出了一種三維點云目標分類和語義分割神經網絡-Pointnet，該模型保證了輸入點云的排列不變性，學習每個輸入點對應的空間編碼并通過對稱函數得到全局特征，Pointnet為從目標分類到場景語義分析應用程序提供了統一的體系結構，測試效果證明該模型的有效性和優越性。

針對Pointnet網絡無法獲得空間點局部結構信息的問題，文中將方向卷積編碼方式應用到深度卷積網絡中，通過對由FPS算法選取的局部區域中心點進行3次方向編碼卷積來捕獲局部形狀特征。同時，針對點云數據旋轉性會造成目標識別結果不穩定的問題，引入空間變換網絡(STN，spatial transform network)來使點云目標識別模型具有空間不變性，從而進一步提高目標識別精確度和魯棒性。在ModelNet40、ShapeNetCore數據集上的實驗結果表明了文中提出的點云目標識別方法的有效性和優越性。

1 三維點云數據特征

1.1 旋轉性

在獲取點云數據時，三維掃描設備的旋轉會導致不同時刻采集的同一點云目標的空間坐標信息(x,y,z)發生旋轉變化，如圖1所示。

圖1 點云旋轉性

雖然圖1中的(a)和(b)是相同點云，但坐標值因為經過旋轉變化而發生改變，對應的卷積操作結果分別入式(1)和式(2)所示：

Ga=Conv(K,[e1,e2,e3,e4,e5])

(1)

Gb=Conv(K,[f5,f4,f3,f2,f1])

(2)

其中:G為卷積結果，e1～e5和f1～f5為輸入點云的各個點的坐標信息，Conv(·)為卷積操作。

根據式(1)～(2)的計算結果，Ga≠Gb。雖然(a)和(b)是相同的點云，但是因為經過旋轉，坐標發生改變，卷積結果也不同，所以卷積操作對點云的旋轉變化不具有魯棒性。文獻[12]采用T-net姿態對齊網絡對點云的旋轉特征進行學習，但是受限于訓練數據規模，以及點云旋轉特征難以捕捉等問題，模型效果還有待提高。因此，文中提出一種空間變換網絡來更好地解決點云旋轉性問題。

1.2 排列不變性

三維點云通常呈無規則隨機分布，且點與點之間沒有順序之分，具有排列不變性，每一組點云數據可以有N！(N為點數)種排列方式，即相同的點云可以有N！種矩陣表示，如圖2所示。

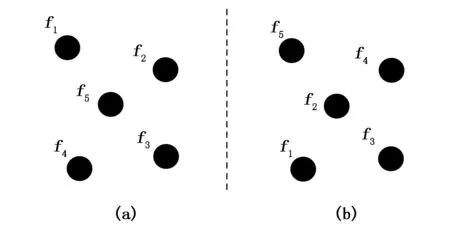
圖2 點云排列不變性

圖2中， (a)和(b)是相同的點云數據，但矩陣表示不同。假設分別對(a)、(b)中的點云數據進行卷積操作，如式(3)～(4)所示：

Ga=Conv(K,[f1,f2,f3,f4,f5])

(3)

Gb=Conv(K,[f5,f4,f3,f2,f1])

(4)

其中：G為卷積結果，f1～f5為輸入點云的各個點的坐標信息，Conv(·)為卷積操作。

根據式(3)～(4)的計算結果，Ga≠Gb。雖然(a)和(b)是相同的點云數據，但是因為矩陣表示不同，卷積結果也不相等，所以卷積操作無法保證點云的排列不變性。因此，將點云數據直接輸入到傳統卷積神經網絡的進行學習的方法存在困難。為了解決上述問題，文中采用max-pooling池化操作解決點云數據排列不變性問題。

2 三維點云目標識別模型

2.1 空間變換網絡(STN)

為了使三維點云目標識別模型具有空間不變性，即對于發生旋轉變換的點云輸入，模型仍能夠對其正確進行分類，本文采用空間變換網絡(STN,spatial transform networks)來自適應三維點云的旋轉變換，將數據進行空間變換和對齊[13]。STN由本地化網絡(Localisation network)、網格生成器(grid generator)及采樣器(sampler)3個部分構成，如圖3所示。

圖3 STN 結構

本地化網絡以feature map或者是點云數據為輸入，輸出為空間變換所需的參數θ，變換矩陣可以為任意形式。網格生成器通過θ和定義的空間變換方式得出輸出V與輸入U的映射T(θ)，即實現點云坐標的對應關系，如式(5)所示：

(5)

輸出V的所有坐標點是先定義好的，根據Aθ和V中每個坐標就可以計算出輸入U的坐標，為了使求得的U中的坐標為整數，利用雙線性差值法進行取值，采樣器根據該坐標點獲取到U中的特征，并將其填充到輸出V中，如式(6)所示：

(6)

STN可用于輸入層，也可插入到卷積層或者其它層的后面，不需要改變原 CNN模型的內部結構[14]。

2.2 深度卷積點云特征提取網絡

將STN應用到傳統的深度卷積神經網絡中，以避免三維點云旋轉性造成的網絡識別結果不穩定，并采用max-pooling差異化對稱函數來解決因點云數據排列不變性導致的點云數據無法

直接輸入到傳統CNN網絡的問題，搭建的深度CNN點云特征提取網絡入圖4所示。

圖4 點云特征提取網絡結構

網絡中重復的mlp是通過共享權重的卷積實現的，第一層是1×3卷積核(對應三維坐標輸入)，之后都是1×1大小的卷積核。經過兩個空間變換網絡和兩個mlp之后，將原始輸入的三維特征映射到高維空間，通過max-pooling層得到1×1 024的全局特征。最后經過全連接層得到k個score，連接Softmax輸出層得到分類結果。

針對圖4中點云特征提取網絡無法提取點云局部拓撲特征的問題，引入了方向卷積編碼方法，如圖5所示。

圖5 點云局部特征提取網絡

首先，采用FPS采樣方法[15]選取局部區域中心點，具體過程為：先隨機選擇一個點，再以離此點最遠的點為起點繼續迭代，直至獲得需要的點數，該方法相比隨機采樣能夠更完整得通過區域中心點采樣到全局點云。

然后，對中心點分別沿X，Y和Z軸3個方向進行3級編碼卷積來捕獲局部形狀特征，將中心點的特征放入張量M∈R2×2×2×d，三階段定向卷積如式(7)～(9)所示：

M1=g[Convx(Ax,M) ]∈R2×2×d

(7)

M2=g[Convy(Ay,M1) ]∈R2×d

(8)

M3=g[Convz(Az,M2) ]∈R1×d

(9)

Ax,Ay,Az是要優化的卷積權重，Convx,Convy和Convz是沿X，Y和Z軸方向的卷積，g是激活函數。經過方向編碼卷積后，每個點被表示為能夠以方向編碼方式表示中心點周圍的形狀圖案的d維度的矢量。

2.3 點云目標分類

Softmax回歸是邏輯函數在多類分類問題上的推廣[16]，其可以將一個含任意實數的K維向量映射到到另一個K維實向量中，并保證向量中每個元素值都在 (0,1) 之間且所有元素的和為1。文中采用Softmax回歸函數對上一節深度卷積網絡提取的全局特征進行處理，得到每一個類別的概率值，如圖6所示。

圖6 點云目標分類結構

對于給定樣本，Softmax回歸預測的是屬于某一類別的概率如式(10)所示：

(10)

其中:x為樣本，c是類別，wc是第c類的權重向量。

3 試驗結果與分析

實驗的硬件環境為Intel Xeon W-2123處理器，Tesla v100 32G顯存顯卡。

3.1 三維點云目標識別

實驗使用ModelNet40[17]和ShapeNetCore[18]兩個形狀分類基準數據集來驗證模型的性能。ModelNet40數據集是由40類人造目標產生的12 311個數據樣本組成，該數據集將其中9 843個數據模型作為訓練集，剩余2 468個數據作為測試集。而ShapeNetCore數據集更為豐富，有高達51 300數據樣本總數，分為55個類別，數據集按70%/10%/20%的比例劃分為訓練機、驗證集和測試集。

網絡模型疊加不同區域的局部特征獲得的全局特征可進一步用于目標識別，如圖5網絡結構所示。 在網格表面區域均勻的選取1 000個點，將每個點的空間坐標歸一化后輸入到網絡模型中，同時為了提高模型的泛化能力，采用數據增強[19]的方法，對點云數據繞Z軸隨機旋轉一定角度，并在每個點的空間坐標加上均值為0標準差為0.02的高斯噪聲。

在相同數據集上使用基于體素化、多視角二維圖像的傳統點云數據處理方法，以及PointNet基準點云處理卷積網絡來和文中提出的直接輸入數據的三維點云目標識別模型作對比，得到的結果如表1和表2所示。

表1 不同模型在ModelNet40上的目標分類效果比較

表2 不同模型在ShapeNetCore上的目標分類效果比較

從表1～2可以看出，文中提出的點云識別模型相比于基于體素的方法與基準點云模型取得了最佳準確率，文中所提點云卷積網絡模型直接采用點云數據輸入，避免了復雜的手工提取特征過程。相比于點云基準網絡PointNet，文中所提模型加入了方向卷積編碼模塊具備利用點云局部特征的能力，在兩個數據集上準確率分別提升了1.2%、1.4%。

3.2 網絡模型結構驗證分析

三維點云目標經過剛性旋轉后的坐標信息將發生改變，為了克服點云目標旋轉所造成的識別結果不穩定，在已有的深度卷積網絡結構中引入STN方法來自適應的將數據進行空間變換和對齊，和其它對無序點云輸入數據處理方法在ModelNet40數據集上進行對比，結果如表3所示。

表3 STN網絡對模型準確率的影響

從表3中可以看出，在輸入層之后加入STN之后，模型的識別率提高了1.3%。此外，對STN加入正則化約束以后，識別率進一步提高了0.4%。本次實驗輸入的點云數據僅包含(x,y,z)三維坐標信息，在處理更高維的點云輸入數據(如包含RGB顏色信息)時，采用正則化約束的識別效果將有更大的提升。

由于實際采集的點云數據的點云位置信息易受到腐蝕，部分點云數據會產生丟失，從而造成點云密度分布不均，因此需要進一步驗證文中所提模型對采樣數據的魯棒性。在ModelNet40數據集上測試不同實驗條件下的分類精確度，如圖7所示。實驗條件為隨機刪除一定比例的采樣點數。

圖7 不同數據缺失比例下的識別率變化

從圖7可以看出，在60%采樣點丟失的情況下，文中所提模型分類準確率僅下降了7.4%，實驗結果表明了點云方向編碼卷積網絡模型在處理輸入數據缺失和不均勻時有較強的魯棒性。

3.3 網絡模型可視化

深度卷積點云目標識別網絡實質上將輸入的低維特征(N*3)映射到高維特征(N*1 024)，再采取對稱函數(max-pooling)來綜合得到全局特征，整個網絡結構如圖5所示。為便于分析，將進入對稱函數前一層的特征進行可視化，具體做法是標注在每個維度上取最大值的點云數據點坐標，得到這些標注的關鍵點坐標與原始點云目標如圖8所示。

圖8 輸入點云目標(左)與網絡模型提取的關鍵點(右)對比圖

所標注的關鍵點決定了最后網絡輸出的全局特征，從圖8中可以看出它們描繪了一個點云目標的大致骨架結構，這樣意味著即使一些非關鍵點數據的缺失也不會影響到網絡的最終判斷，也證明文中提出的卷積點云目標識別網絡的魯棒性。

4 結束語

鑒于已有的深度卷積點云目標識別模型無法有效提取點云局部拓撲特征，文中通過FPS算法選取局部區域中心點，并對中心點進行3次方向編碼卷積來捕獲點云目標局部形狀特征。同時，采用空間變換網絡來解決因點云數據旋轉性會造成導致的目標識別結果不穩定問題，進一步提高了目標識別精確度和魯棒性。文中提出的點云目標識別方法有效提高了識別精度，相較于PointNet在ModelNet40和ShapeNetCore兩個數據集分別提高1.2%和1.4%。