基于多時差的干擾源定位虛假點消除方法
柏如龍,霍立寰*,陳 兵,王海清,江 漫,楊 光,許瑞杰,廖桂生
(1.中國電子科技集團公司第五十四研究所,河北 石家莊 050081;2.河北省電磁頻譜認知與管控重點實驗室,河北 石家莊 050081;3.西安電子科技大學 雷達信號處理國家重點實驗室,陜西 西安 710071)
0 引言
無源干擾源定位技術能夠被動接收電磁波信號對干擾源進行測向定位,是現代電子對抗的重要手段[1-3]。以美國海軍“NOSS”系列的海洋監視衛星為典型代表的基于衛星平臺的時差定位體制,具有覆蓋范圍廣、作用距離遠、接收隱蔽、生存能力強的優點,能夠迅速、準確地發現干擾源目標[4-6],在各領域都有著重要作用和廣泛的應用前景。
目前的衛星時頻差定位主要包括時頻差聯合定位和多時差定位[7-12],利用了不同衛星接收信號間的到達時間差(TDOA)和到達頻率差(FDOA)。相比于時差測量,頻差測量需要更多的參考站進行標校。因此,僅僅基于時差的三星時差定位體制成本更低、定位結果更為可靠。三星時差定位基于兩條時差線進行交會定位,受衛星位置和干擾源位置的影響,兩條時差線在某些時刻存在兩個交點,難以確認干擾源的真實位置。文獻[13-18]的研究主要集中在時差測量優化、定位方程解算等方面,包括不同體制信號的時差測量和校正方法,以及在不同定位場景下的定位方法。對于定位過程中出現的虛假點目標,僅基于目標位置的先驗知識進行區分,當先驗知識缺失時則無法判斷虛假點。因此,亟需提出有效、穩健的虛假點消除方法。
針對上述問題,本文提出了基于多時刻測量的三星時差定位虛假點消除方法。首先建立了基于衛星多時刻測量時差結果的三星時差定位模型,然后基于WGS-84地球橢球模型建立多時刻定位方程組,最后推導了牛頓迭代的求解方法。通過多時刻的測量數據直接獲取干擾源真實位置附近的定位結果,以該定位結果為初始值進行逐時刻精確定位。該方法能夠在去除虛假點的基礎上,得到更高精度的定位結果;同時在先驗初始值偏差和時差測量誤差較大的情況下仍具有良好的穩健性。
1 多時刻時差定位模型
圖1為建立大地坐標系模型,包括地球橢球、指向0°經度方向的X軸,指向北極方向的Z軸,以及根據右手定則得到的Y軸。主星接收到干擾源信號,兩顆輔星能夠收到干擾源的旁瓣信號。每個時刻能夠測量得到主星和輔星一、主星和輔星二的兩個到達時間差,形成如圖所示的時差面,在假設目標零高程的條件下,兩個時差面和地球橢球面的交點即為三星定位的結果。由圖1可以發現,兩個時差面相交于一條直線,該直線與地球橢球面相交于兩個點,一個為干擾源目標真實位置,另一個為虛假位置。在沒有先驗信息的情況下,僅依靠單時刻的時差難以區分真實位置和虛假位置。

圖1 三星干擾源定位示意Fig.1 Configuration of the tri-satellite interference source location
圖2給出了時差線存在虛假點時的時差線相交情況,可以發現,多個時刻的時差線在真實位置處逐漸收斂于一點,而虛假點位置的時差線相交較為發散。因此,可以利用多個時刻的時差測量結果進行定位,從而判斷出干擾源的真實位置。

圖2 三星時差線相交情況示意Fig.2 Intersection of tri-satellite time difference line
假設干擾源的坐標為(x,y,z),第p個時刻時主星坐標為(xp0,yp0,zp0),輔星一坐標為(xp1,yp1,zp1),輔星二坐標為(xp2,yp2,zp2),干擾源與輔星一和輔星二在第p個時刻的時差測量值分別為τp1和τp2,滿足:
(1)
式中,c為光速,rp0,rp1和rp2分別為干擾源與主星、輔星一和輔星二在第p個時刻的距離。
根據距離的計算方式,以及地球橢球面模型,構造如下定位方程組。

(2)
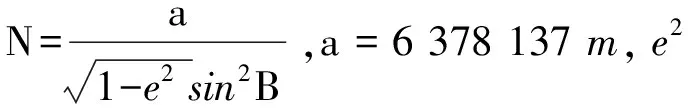
2 迭代求解算法
針對多時刻的測量結果構成的定位方程組,直接求解較為困難,考慮采用牛頓迭代方法求解。將以上方程組進行如下表示:
(3)
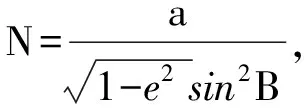
F(x,y,z)=0。
(4)
相應的Hesse矩陣為:
(5)
若第k次迭代中干擾源坐標為Pk=(xk,yk,zk),則根據下式進行迭代。
Pk+1=Pk-[F′(xk,yk,zk)]-1F(xk,yk,zk)。
(6)
基于多時刻的三星定位方法步驟如下:
步驟1:根據P個時刻的時差τp1和τp2,計算對應的主輔星與干擾源的距離差(rp1-rp0)和(rp2-rp0);
步驟2:初始化,設迭代次數k=0,干擾源目標初始位置P0;
步驟3:計算該次迭代過程中的Hesse矩陣F′(xk,yk,zk),并根據式(6)得到下一次迭代中干擾源位置的估計結果Pk+1;
步驟5:判斷目標運動屬性,若為運動目標,則輸出的定位結果作為初始值,對每個時刻的測量結果利用球形迭代方法得到定位結果的精確值。
算法流程如圖3所示。
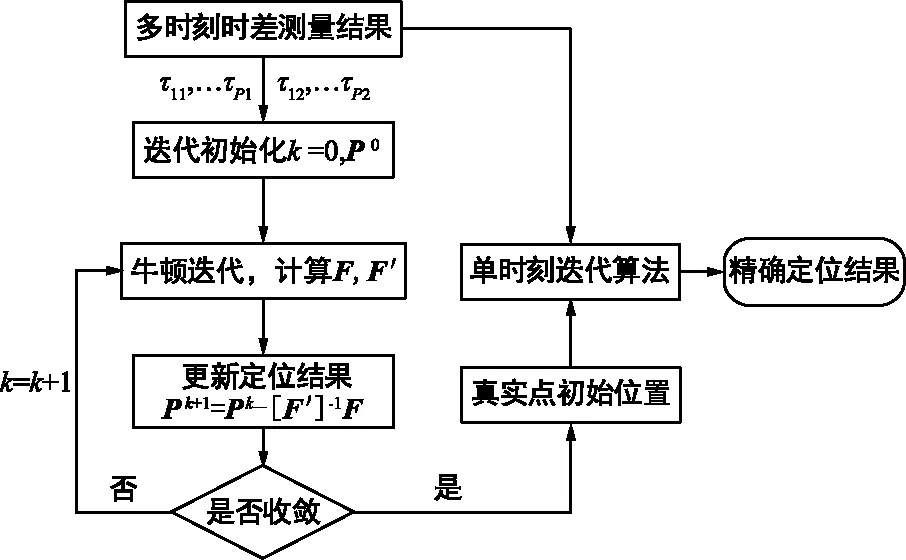
圖3 基于多時刻測量的三星定位方法Fig.3 Tri-satellite localization method based on multi-time TDOA
3 仿真實驗
在下面的仿真試驗中,單時刻定位中定位時刻個數P=1,多時刻定位中定位時刻個數P>1,所提方法為利用多時刻定位去除虛假點后,將得到的定位結果作為單時刻定位的初始迭代值的方法。
3.1 多時刻定位影響因素分析實驗
多時刻定位的性能主要與選取時刻個數、時間總長度有關,通過仿真實驗探究其變化關系,如圖4所示。
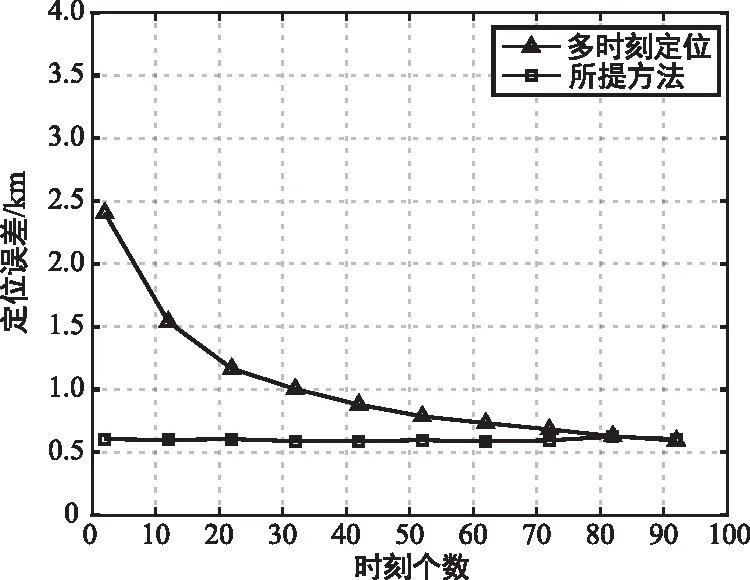
(a) 定位誤差隨時刻個數變化情況
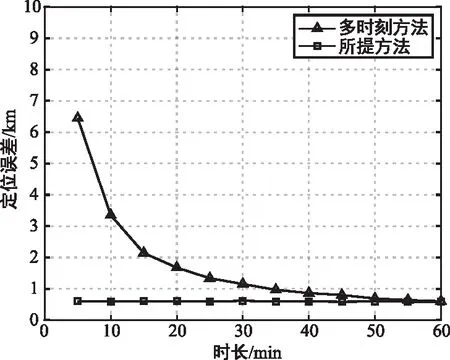
(b) 定位誤差隨時長變化圖4 多時刻定位方法性能影響試驗Fig.4 Performance experiment of the multi-time location method
干擾源位置為125°E,30°N,時差測量誤差為0.5 μs。首先仿真了時間總時長為20 min,多時刻定位和所提方法的定位誤差隨采用時刻個數的變化關系,可以發現:多時刻定位性能隨時刻個數增加而提高,并不斷趨近于所提方法,所提方法的定位誤差基本不變。然后仿真了采用時刻個數為10,多時刻定位和所提方法的定位誤差隨總時長的變化關系,可以發現:多時刻定位性能隨總時長增加而提高,并不斷趨近于所提方法,所提方法的定位誤差同樣保持穩定,能夠實現高精度地快速定位。
3.2 迭代初始值影響實驗
通過仿真實驗,對比迭代初始值對算法的性能影響。干擾源目標位置為125°E,30°N,時差測量誤差在±0.5 μs內均勻分布,蒙特卡洛次數為500,采用3個連續時刻測量得到的時差值進行去除虛假點的目標定位,時間間隔為5 min,迭代初始值誤差為初次迭代的先驗經緯度偏差的均方根誤差。圖5給出了迭代初始值誤差在0°~20°情況下,單時刻定位、多時刻定位和所提方法定位誤差隨迭代初始值誤差的變化關系。可以發現:當迭代初始值逐漸增大時,單時刻定位的定位誤差惡化明顯,多時刻的定位方法基本不受迭代初始值的影響,但是在迭代初始誤差很較小時,定位效果相比單時刻定位較差。而所提方法在多時刻定位的基礎上,能夠獲得同時優于單時刻和多時刻的定位精度。
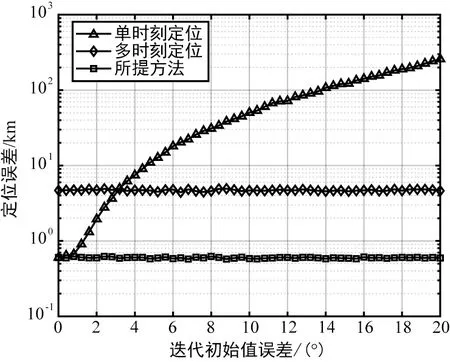
圖5 不同方法的定位誤差隨迭代初始值誤差的變化關系Fig.5 Location error of different methods versus the initial value error of the iteration
3.3 測量誤差影響實驗
對比3種方法隨時差測量誤差的變化關系如圖6所示。干擾源目標位置為125°E,30°N,多時刻定位采用5個連續時刻測量得到的時差值以去除虛假點,時間間隔為4 min,迭代初始值偏差的均方根為1°,蒙特卡洛次數為500。可以發現,隨著時差測量誤差增加,3種方法的定位誤差增大。其中,單時刻定位在時差測量誤差較小時,主要受迭代初始值影響,受時差測量誤差影響不明顯。多時刻定位方法由于采用解方程組的方式,受時差測量誤差影響較大。而基于多時刻測量的單時刻定位方法,在時差測量誤差增大時具有良好的穩健性。

圖6 不同方法的定位誤差隨時差測量誤差的變化關系Fig.6 Location error of different methods versus the TDOA measurement error
4 實測數據驗證
圖7為某次實測數據的處理情況。
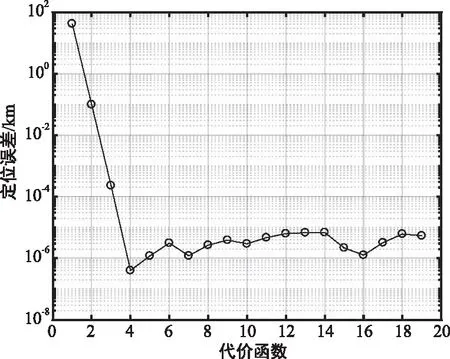
(a) 代價函數變化情況
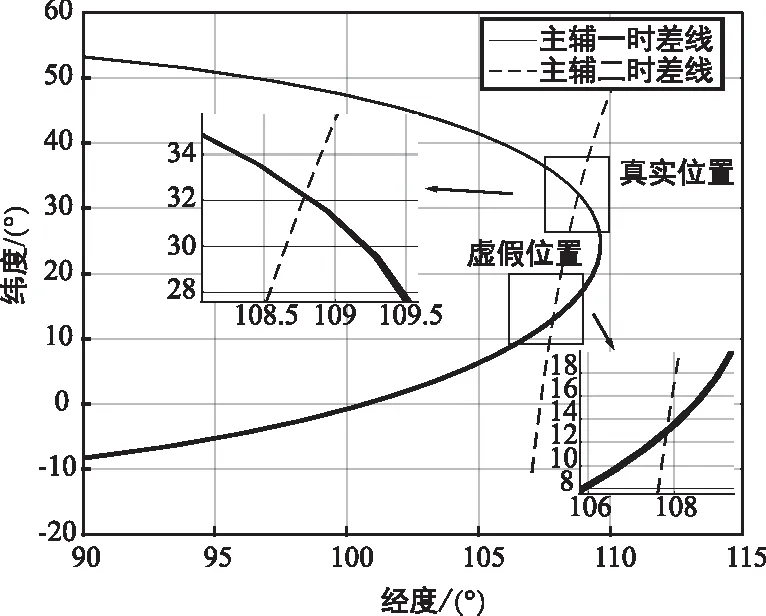
(b) 時差線相交情況圖7 某次實測數據處理結果Fig.7 Results of the real data processing
實測數據處理后,多時刻定位方法能夠定位誤差為23.11 km,基于多時刻測量的方法得到定位誤差為9.33 km。從迭代過程中代價函數δ的變化情況可以看出,進行迭代2~3次即可得到滿足要求的結果。從時差線相交情況可以看出,由于時差測量存在誤差,真實點位置多時刻的時差線也未能完全相交于一點。相比于真實點位置,虛假點處的時差線更為發散,因此能夠采用基于多時刻測量的方法去除虛假點。多時刻定位算法能夠定位至輻射源目標真實位置附近,然而精度受時差測量誤差影響,難以得到較高的定位精度。而所提方法通過后續的逐點定位,在去除虛假點的基礎上,能夠大幅提高多時刻的定位精度。
5 結束語
三星時差定位通過兩條時差線的交點確定干擾源位置,然而,若兩條時差線存在兩個交點時,則難以確定真實點位置。本文提出基于多時刻測量的虛假點消除方法。該方法利用多個時刻的時差測量數據判斷干擾源真實位置所在區域,然后將該結果作為單時刻定位方程牛頓迭代方法求解的初始值,最終得到去除虛假點后高精度的定位結果。仿真實驗分析了對定位性能的影響因素,驗證了較大測量誤差下和先驗初始值偏差情況下的穩健性,實測數據處理結果驗證了所提方法能夠有效、快速地得到較高精度的定位結果。

