由幾個錯誤看懂初中幾何解題
黃志強



摘要:學生的常見錯誤有以下幾個,一是對條件的分析不全面,二是不善于從全局出發處理條件,三是錯用濫用三角形全等。分析幾何題主要有兩種方法:綜合法,分析法。
關鍵詞:條件分析;綜合法;分析法
筆者執教初三數學也有好幾年,久而久之也就明白了學生在解題方面有哪些困惑,讓我印象最深的是學生對幾何題的一籌莫展。有些同學由于學習不得法,甚至有放棄學習幾何的念頭,有些同學雖然能學得下去,但在解題時往往抓不住解題思路,胡寫亂寫。針對學生出現的問題,我總結了一套幾何題的解題策略。現對學生學習幾何出現的問題進行分析并提出解題策略,希望能有拋磚引玉的作用。
一、學生常出現的幾個錯誤
案例分析:學生對條件逐個分析,是很多學生的選擇的方法,這里學生由第一個和第二個條件得出了DA=DC這一個關鍵結果,但是離證明四邊形AECD是菱形還差一步,就是證出四邊形AECD是平行四邊形。其實學生在處理條件是應該統觀全局,在解題之前應該先把題目全部看完,不要著急分析第一個條件,應該在看完題目后觀察哪些條件可以聯合分析。比如在這道題中,可以先將AB∥DC, CE∥AD這兩個條件聯立分析,即可得出四邊形AECD是平行四邊形。
(三)錯用濫用三角形全等
案例三:如圖,AD是△ABC的角平分線,過點D作AC和AB的平行線,交AB于點E,交AC于點F。求證:四邊形AEDF是菱形。
學生解答:
∵DE∥AC
∴∠EDA=∠FAD
∵DF∥AB
∴∠EAD=∠FDA
∵AD=AD
∴△ADE≌△ADF
∴AE=AF
案例分析:在這道題中,學生試圖通過三角形全等證明AE=AF,但是AE與AF并不是對應邊,所以AE≠AF,除了此處錯誤,學生還存在忽略條件的情況,忽略了AD是△ABC的角平分線,由這個條件,可得∠EAD=∠FAD,結合學生前面得到的∠EDA=∠FAD,可得∠EAD=∠EDA,則AE=DE,再通過DE∥AC,DF∥AB可以證出四邊形AEDF是平行四邊形,又由AE=DE即可得出平行四邊形AEDF是菱形。在這道題中,反映了學生在證等邊時過于依賴三角形全等這一知識點,其實證明兩條線段相等除了可以用三角形全等的性質,還可以用線段中垂線的性質、角平分線的性質、等腰三角形的性質等。
二、幾何題常見解題策略
不可否認,幾何證明題是初中難度比較大的一種題型,其沒有一個固定的公式,題目也千變萬化,解法更是多種多樣,但是萬變不離其宗,以上學生出現的問題主要是對題目的分析不得法,分析幾何題主要有兩種方法和一個重要習慣。
(一)綜合法
從已知條件出發,通過有關定義、定理、公理的應用,逐步向前推進,直到問題解決。
案例:如圖,![]() ABCD的對角線AC,BD相交于點O,EF過點O且與AD,BC分別相交于點E,F.求證:OE=OF.(圖中∠1指∠EAO,∠2指∠FCO)
ABCD的對角線AC,BD相交于點O,EF過點O且與AD,BC分別相交于點E,F.求證:OE=OF.(圖中∠1指∠EAO,∠2指∠FCO)
(綜合法)分析過程:
綜合法是學生比較常用的一種幾何題分析方法,但是在使用時要注意以下幾點,一是注意結論有效性。在這道題目中,![]() ABCD可以推出很多結論,比如對邊相等且平行,對角相等,對角線互相平分等,但在后續的分析中可以發現,對角相等和對邊相等對解題并沒有作用,應該舍棄這兩個結論。二是注意多級推導,比如從
ABCD可以推出很多結論,比如對邊相等且平行,對角相等,對角線互相平分等,但在后續的分析中可以發現,對角相等和對邊相等對解題并沒有作用,應該舍棄這兩個結論。二是注意多級推導,比如從![]() ABCD用這個條件分析到對邊平行,還應由對邊平行分析到內錯角相等。三是注意條件的全局處理。如在案例三中,應該先將多個條件聯合分析排在優先位置。
ABCD用這個條件分析到對邊平行,還應由對邊平行分析到內錯角相等。三是注意條件的全局處理。如在案例三中,應該先將多個條件聯合分析排在優先位置。
(二)分析法
分析法就是從命題的結論考慮,推敲使其成立需要具備的條件,然后再把所需的條件看成要證的結論繼續推敲,如此逐步往上逆求,直到已知事實為止。可見分析法實際上是運用逆向思維的過程。
所謂的逆向思維,其實就是指人們在看待問題時,從與常規思維相反的角度進行思考和分析,從而找到問題解決的途徑,逆向思維模式可以很好地幫助學生打破原本傳統數學思維模式的局限。
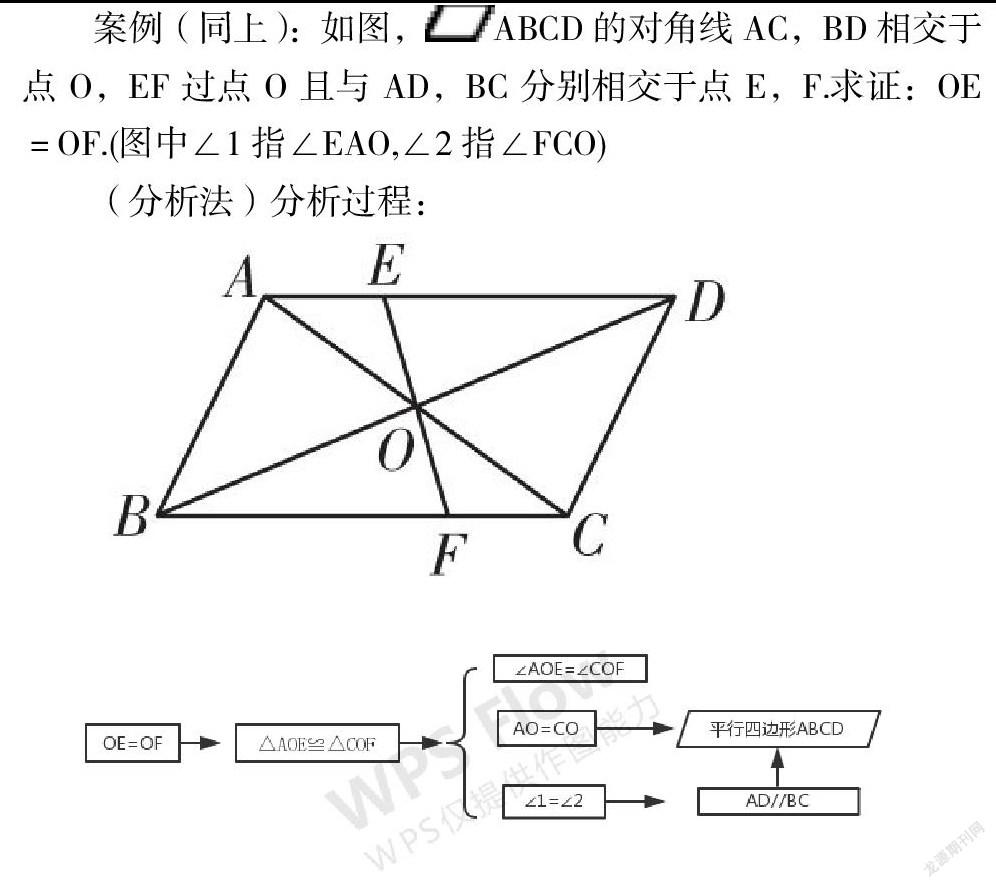
案例(同上):如圖,![]() ABCD的對角線AC,BD相交于點O,EF過點O且與AD,BC分別相交于點E,F.求證:OE=OF.(圖中∠1指∠EAO,∠2指∠FCO)
ABCD的對角線AC,BD相交于點O,EF過點O且與AD,BC分別相交于點E,F.求證:OE=OF.(圖中∠1指∠EAO,∠2指∠FCO)
(分析法)分析過程:
在這道題目中,我們要證明的結論是OE=OF,觀察圖形,可以發現OE和OF分別是△AOE和△COF中的兩條邊,因此我們聯想到證明這兩個三角形全等,再通過分析題目條件,可以由![]() ABCD提供AO=CO,AD//BC。其中AD//BC可以推出∠EAO=∠FCO,
ABCD提供AO=CO,AD//BC。其中AD//BC可以推出∠EAO=∠FCO,
再由∠AOE=∠COF,完全可以得到△AOE和△COF全等。至此,思路已經出來了。
分析法是一種重要的數學方法,它從結果出發,尋找使結果成立的條件,在解題中往往比綜合法更快捷,更有針對性。分析好之后還是要用綜合法的形式寫出過程。
(三)解題習慣
現在發現很多學生在解幾何題時會立刻寫解題過程,并沒有認真看完整道題,也沒有畫出思路圖。學生在讀題的時候發現的每個條件要在所給的圖形中標記出來。如給出對邊相等,就用邊相等的符號來表示。有一些隱含的條件更加要標示出來,如對頂角相等。除此之外是要牢記題目給出的條件。題目的條件不僅要標記,還要記在腦海中,做到不看題,就可以把題目復述出來。
尋找幾何題的解題思路既可以用綜合法也可以用分析法,有時可能要兩種方法同時使用,兩種方法各有優缺點,而且要有作標記的良好習慣。學生要學好幾何,不能一蹴而就,要大膽去練,去分析,去總結,讓自己對兩種方法能夠應用自如,學幾何也就會變成一件有趣的事情了。
參考文獻:
[1]魏堆付.初中數學教學中學生逆向思維能力的培養策略[J].數學學習與研究,2021(14):142-143.
[2]薛盛初.談數學教學中學生自學能力的培養[J].中學數學研究.

