智能全向移動平臺的里程計系統誤差校正
朱文亮 司文展* 朱加豪 周云鵬
(1、江蘇海洋大學機械工程學院,江蘇 連云港 222005 2、鹽城工學院機械工程學院優集學院,江蘇 鹽城 224007)
近年來,智能移動機器人是廣大科研工作者的研究熱點,在移動機器人相關技術研究中,自主導航技術是其研究的核心,而定位是完成導航的前提和基礎[2]。
定位是指通過傳感器確定移動機器人在其運動環境中的坐標,根據定位過程分為絕對定位和相對定位[3]。其中輪式里程計定位是一種最廣泛使用的相對定位方法。里程計使用編碼器為移動機器人提供基本的位姿估計,這種方法稱為航跡推算法,能夠在短期內提供較高的定位精度,航跡推算是一個累加的過程,隨著運行距離的增加,會產生誤差累計,所以減少里程計誤差具有重要的意義[4]。
里程計系統誤差主要是由于移動機器人設計不合理以及制造精度較低等因素引起,所以通過校核系統參數(輪徑和輪距)可以減少系統誤差[5]。在麥克納姆輪式移動平臺里程計定位過程中,系統誤差主要來源于包括車輪實際直徑與測量直徑不相等、有效輪距安裝誤差等。
1 智能全向移動平臺的運動學分析
傳統的移動平臺轉彎時需要適宜的轉彎半徑,在狹小空間轉彎時,有時需要不停地進行停車再調整,降低了物流效率。為了適應狹窄的工作環境和降低倉儲空間成本,本文設計了一款麥克納姆輪式的全向移動平臺。為方便分析智能全向移動平臺的運動學特征,假設運動環境是平面,忽略運動地面不平整對運動的影響,忽略車輪和地面的打滑。
建立運動學物理模型:
如圖1(b)所示,移動平臺輥子如圖示安裝,剛體在平面內的運動可以分解為三個獨立分量:X 軸平動,Y 軸平動,yaw 軸自轉,如上圖所示,移動平臺底盤的運動也可以分解為三個量:Vx為X 軸運動的速度,即上下方向,定義向上為正;Vy為Y 軸運動的速度,即左右方向,定義向左為正;ω 表示yaw 軸自轉的角速度,定義逆時針為正,以上三個量為移動平臺幾何中心O 的速度。
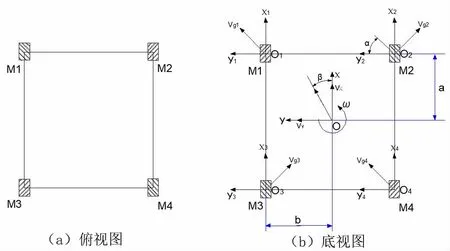
圖1 移動平臺物理模型
M1M2M3M4 為輪1 輪2 輪3 輪4;Oixiyi為與各輪中心固連的坐標系;vi為各輪中心速度;ωi為各輪轉速;vgi為各輥子中心速度;Rn為標稱輪直徑;α 為輥子方向與輪轂的夾角[6]。逆運動學問題就是將底盤坐標系Oxy 下的線速度和角速度轉換為4 個驅動麥克拉姆輪的速度。

麥克納姆輪的輪轂軸與輥子轉軸呈45°。理論上這個夾角可以是任意值,根據不同的夾角可以制作出不同的輪子,但從結構、力學特性、運動學特性來講45°是最優異的[7]。將α=45°代入

正運動學問題就是將4 個驅動麥克拉姆輪的速度轉換為底盤坐標系Oxy 下的線速度和角速度。正運動學模型可以根據逆運動學模型解出來。
2 基于行程法的校正方法
本文提出了校正里程計系統誤差的方法-行程法,并設計校正實驗確定校正參數。該校正方法分別考慮了系統誤差對機器人直線運動和旋轉運動的影響,通過直線運動和旋轉運動的實驗數據確定校正參數[1]。
本次實驗利用課題組自主研發的麥克納姆輪式智能移動平臺,該移動平臺的四個輪子通過四個伺服電機完全獨立驅動(圖2)。

圖2 麥克納姆輪式智能移動平臺
智能移動平臺里程計的原理就是ROS 平臺發布線速度和角速度指令,通過逆向運動學方程解析為每個輪子的轉速指令,移動平臺運動時,采集四個輪子的編碼器反饋數據,結合正向運動學方程,計算出移動平臺的瞬時位姿。
當移動平臺的瞬時位姿達到目標位姿時停止,此時停下的位姿與目標位姿產生的誤差,需要校正,如圖3 為里程計系統工作過程流程圖。

圖3 里程計系統工作過程流程圖
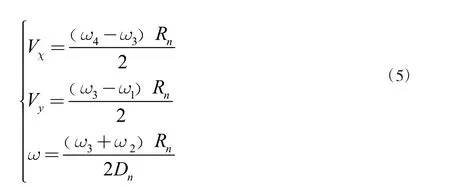
由輪直徑測量誤差導致的誤差ER對移動平臺位置定位產生影響, 輪距的安裝誤差導致的誤差ED對移動平臺位姿定位產生影響,其中

式中,Ra為實際輪直徑,Rn為標稱輪直徑,Da為實際輪距,Dn為標稱輪距[8]。把誤差系數代入運動學模型中,其中,逆運動學模型

正運動學模型

以輪1 為例,將引用誤差系數后的Vx、Vy、ω 轉化為伺服電機的轉速,即

將引入校正系數后的運動學模型在程序中實現,設計簡易校正軟件方便測試系數真值,如圖4 是利用ROS 機器人操作系統設計的界面。
如圖4 所示,test_distance 表示測試距離,即給定的移動平臺運動距離;test_angle 表示測試角度,即給定的移動平臺自轉角度;speed 表示測試速度;odom_linear_correction 表示直線校正系數;odom_angular_correction 表示自轉校正系數。

圖4 操作界面
為了保證數據可靠性,直線運動速度分別取1m/s、1.5m/s、2m/s ,運行距離為3 米;旋轉運動速度分別取5°/s、10°/s、15°/s, 自轉角度為360°。得到的測試數據如圖5所示,測試時,每種情況測試5 次(直線運動測試校正前,速度為1m/s 為一種情況,以此類推),圖中只記錄每種情況的最大值、最小值和中位數。

圖5 測試數據
3 試驗結果與分析
表1 所示為校正前后移動平臺的位置定位誤差結果,表2 所示為校正前后移動平臺的姿態定位誤差結果。從圖1 可以看出,校核前位置定位測試的均值為3.154m,校核后的均值為3.006m,位置定位精度提高了4.9%,從圖2 可以看出,校正前姿態定位測試的均值為370.11°,校正后的均值為360.5°,姿態定位精度提高了2.7%。

表1 直線運動校正前后實驗數據對比

表2 旋轉運動校正前后實驗數據對比
4 結論
里程計的誤差校正是實現智能全向移動平臺位姿準確估計的前提。所以本文綜合考慮麥克納姆輪式移動平臺系統誤差來源產生的誤差對定位造成的影響,提出了針對輪直徑測量誤差和輪距安裝誤差而引起的里程計系統誤差校正方法。
4.1 實驗結果表明,校正后的系統誤差有明顯改善。
4.2 用數學思維提出了一種邏輯嚴密的里程計系統誤差校正方法,使誤差校正更易操作。
4.3 由于可以根據具體底盤的精度和實驗場地選擇實驗運動的路程和重復次數,故該方法的實驗簡單方便。

