基于離散加筋理論的縱環加筋圓柱殼軸壓后屈曲縮尺模型研究

李正良，王靜超，于偉，朱萬旭

（1.重慶大學土木工程學院，重慶 400045；2.山地城鎮建設與新技術教育部重點實驗室（重慶大學），重慶 400045；3.桂林理工大學土木與建筑工程學院，廣西桂林 541004；4.桂林理工大學廣西建筑新能源與節能重點實驗室，廣西桂林 541004）

新型干式煤氣柜是一種可儲存可燃氣體，是能節約能源和保護環境的大型重要構筑物［1］.新型干式煤氣柜柜體作為一種典型的大型薄壁縱環離散加筋圓柱殼，由于試驗條件和經費的限制，很難對其進行大量的原型結構試驗.目前，較為可行的研究方法是采用縮尺模型的試驗結果結合相似理論預測原型的屈曲承載能力.因此，研究縱環加筋圓柱殼軸壓后屈曲縮尺模型的設計方法和相似原理，對驗證與評估新型干式煤氣柜柜體合理性和安全性顯得尤為重要.

楊金花等［2］研究了具有環向貫穿脫層圓柱殼的屈曲問題，討論了脫層大小、深度、位置以及復合材料纖維鋪層方向對脫層圓柱殼屈曲載荷的影響.結果表明：脫層長度越大、越靠近殼的外表和軸向中心，結構的屈曲載荷越低.向紅等［3］根據Von Karman板理論，建立了具損傷正交各向異性板的非線性壓曲方程.Singhatanadgid 和Ungbhakorn［4］針對壓扭組合荷載作用下的正交各向異性圓板，進行了線性屈曲完全相似和不完全相似研究.結果表明：完全相似模型和采用各向同性材料的不完全相似模型，結合縮尺原理公式，可以較好地預測其原型的屈曲特性，縮尺原理公式適用于具有任意相同邊界條件的一對模型和原型.Hilburger 等［5-6］考慮加筋圓柱殼焊接缺陷的影響，根據結構的半徑與等效厚度比值相等的原則，采用密加筋理論、有限元法和結構試驗相結合的手段，對縮尺模型與原型進行了穩定性設計和試驗，驗證了新方法的正確性；同時給出了加筋圓柱殼模型詳細和實用的設計方法，但尚未給出縮尺模型與原型的屈曲相似關系.賈冬云等［7-8］采用理論分析、有限元模擬和試驗研究相結合的方法，對大型正多邊形煤氣柜立柱、加筋肋和壁板進行了系統的研究.總體而言，現有研究可以解決層合殼、板和密加筋圓柱殼屈曲的縮尺模型設計與相似預報問題，但對于縱環離散加筋圓柱殼屈曲相似的研究頗為缺乏，所以開展基于離散加筋理論的縱環加筋圓柱殼軸壓后屈曲縮尺模型研究非常有必要.

本文以縱環加筋圓柱殼為研究對象，基于離散加筋理論與結構體系的總能量，推導出結構軸壓后屈曲的廣義相似條件與縮尺原理公式.基于酒窩缺陷和焊縫缺陷的函數，建立了含初始缺陷的縱環加筋圓柱殼有限元模型.最后，對含初始缺陷的縱環加筋圓柱殼，開展軸壓后屈曲不完全相似模擬研究，以驗證縮尺模型設計的廣義相似條件和軸壓后屈曲縮尺原理公式的準確性.

1 基于離散加筋理論的加筋圓柱殼軸壓后屈曲縮尺原理

1.1 縱環離散加筋圓柱殼軸壓后屈曲的廣義相似條件

在相似轉換過程中，相似結構體系的數學模型是一致的.因此，任意兩相似結構體系總能量間的關系可表示為：

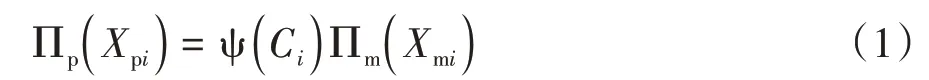
式中：下標p 和m 分別代表原型和模型；Xpi和Xmi（i=1，2，…，n）分別對應原型結構和模型結構的幾何參數和材料參數；ψ（Ci）（i=1，2，…，n）為兩相似結構參數的傳遞函數.根據該函數關系可推導出結構的屈曲縮尺原理公式.

縱環離散加筋圓柱殼結構見圖1、圖2.

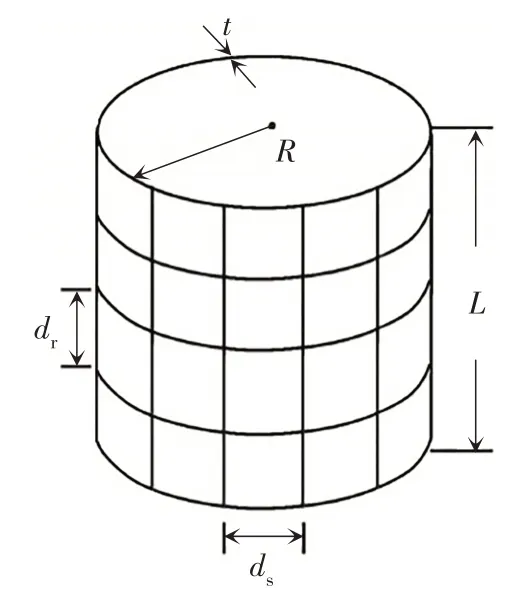
圖1 縱環離散加筋圓柱殼Fig.1 The ring and stringer stiffened-cylindrical shell

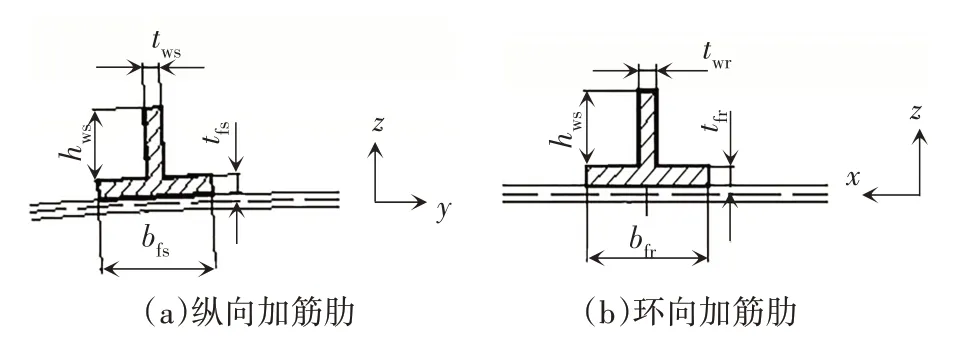
圖2 T型縱環離散加筋圓柱殼的加筋肋截面圖Fig.2 Configurations of the ring and stringer T-shaped stiffened-cylindrical shell

圖中，R為蒙皮半徑，t為蒙皮厚度，L為加筋圓柱殼長度.下標s 和r 分別代表縱向和環向的加筋肋.ds和dr分別表示縱向和環向的加筋肋間距.bfs、tfs和hws、tws分別為縱向T 型加筋肋翼緣和腹板的長度與厚度.bfr、tfr和hwr、twr分別為環向T 型加筋肋翼緣和腹板的長度與厚度.

加筋圓柱殼的能量泛函為［9-10］：

式中：U、UL分別為結構的應變能和外力功.

蒙皮的內力表達式為［10］：

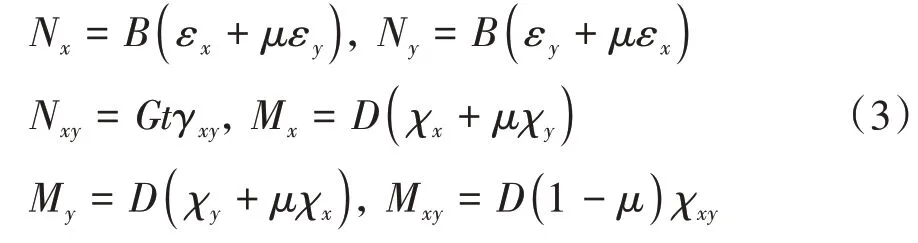
式中：Nx、Ny和Nxy分別為單位長度上對應方向的薄膜內力；Mx、My和Mxy分別為單位長度上對應方向的彎矩；εx、εy和γxy為殼體蒙皮中面的應變；χx、χy和χxy是殼體曲率；μ為蒙皮材料泊松比；B、D和G分別為拉伸剛度、彎曲剛度和剪切模量，具體表達式為

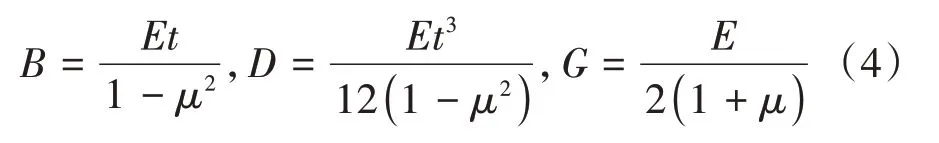
基于Donnell 假定，含初始幾何缺陷圓柱殼的非線性幾何方程為［11］：

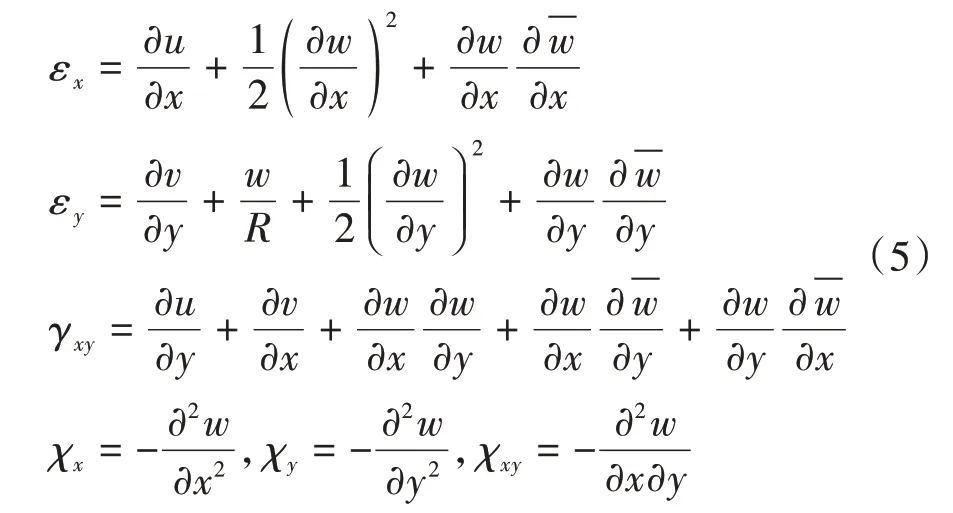
式中：u、v、w分別為圓柱殼的縱向、環向和徑向的位移；為徑向初始幾何缺陷.

加筋肋的非線性幾何方程為［10］：

式中：e為加筋肋形心到蒙皮中面的距離.

為了得到加筋圓柱殼的總能量的具體表達式，引入蒙皮與加筋肋的應變能表達式［10，12］：

式中：U0、Us和Ur分別為蒙皮、縱向加筋肋與環向加筋肋的應變能；es和er分別為縱肋截面形心與環肋截面形心到圓柱殼中面的距離；I0s和I0r分別為縱肋與環肋到圓柱殼中面的慣性矩；A為加筋肋截面面積；N為加筋肋數量；Js和Jr為開口截面型加筋肋的扭轉常量，其具體表達式為［13］

基于離散加筋理論的加筋圓柱殼應變能表達式為：

軸壓作用下結構的外力功表達式為［10］：

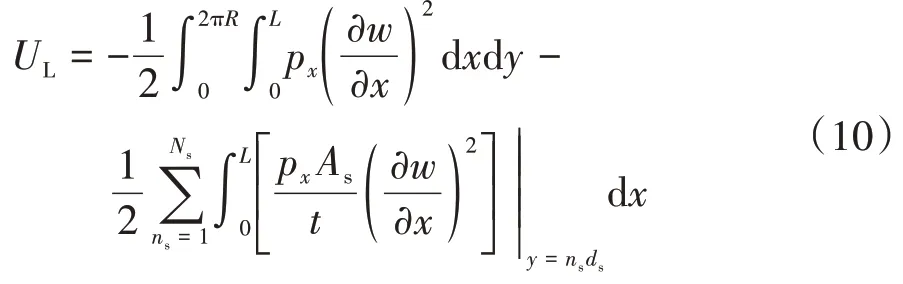
式中：px為殼體軸向均布荷載.

根據狄拉克函數的性質［14］：

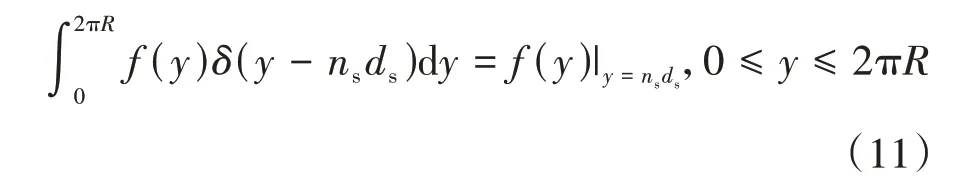
式（10）可以轉化為：

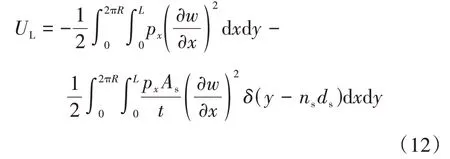
首先，將式（3）、式（5）和式（6）代入式（7），推得式（9）的具體表達式.然后，將式（9）和式（12）代入式（2），得到加筋圓柱殼的總能量表達式為：

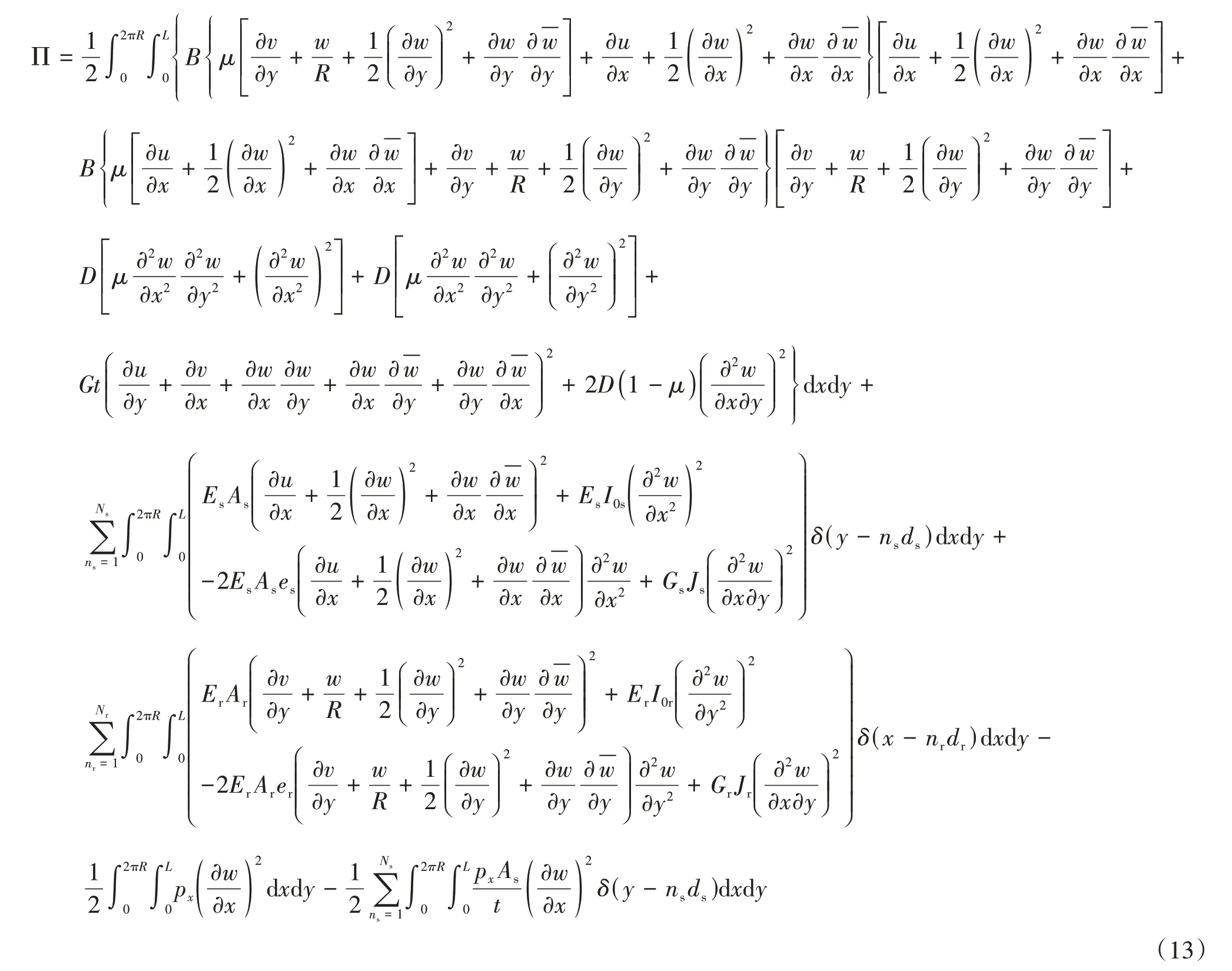
原型結構參數可由模型結構參數和縮尺因子Ci表示：

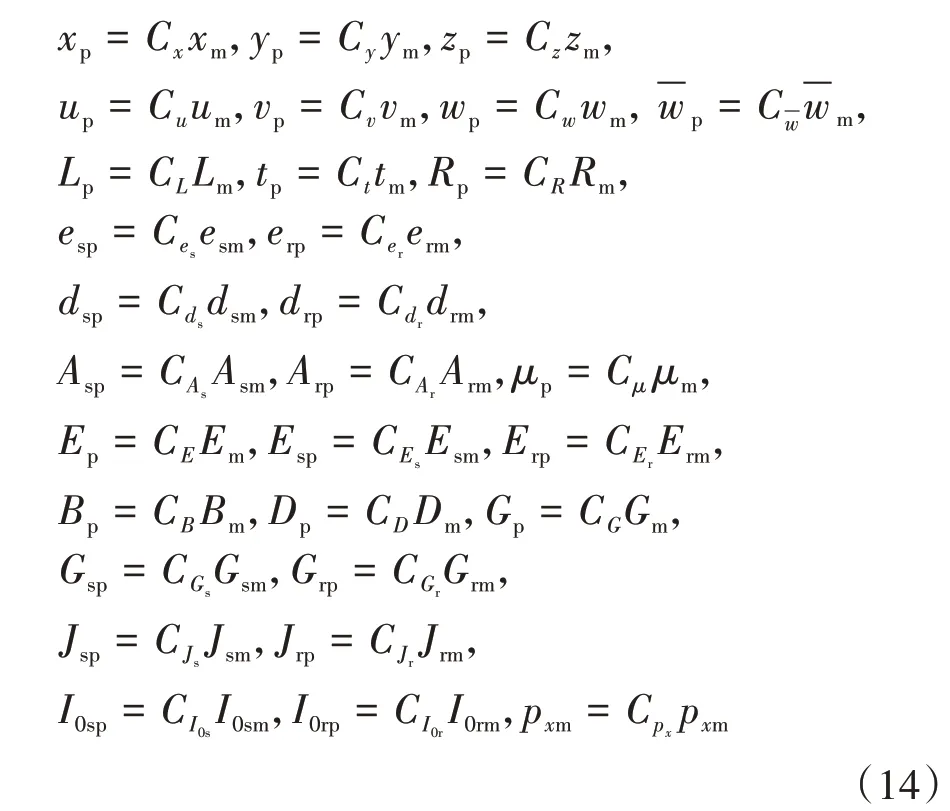
當兩相似結構的蒙皮完全幾何相似時，即Cx=Cy=Cu=Cv=Cw=CR，并利用δ(ax)=δ(x)∕|a|［14］，將式（14）代入式（13）進行相似轉換，可得模型和原型的廣義相似條件：

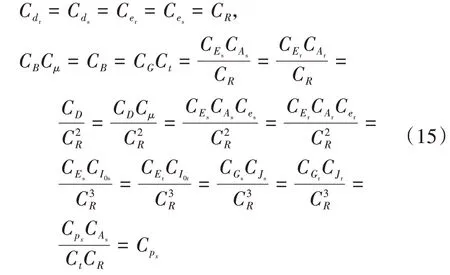
基于式（15），進一步推導得到模型與原型需滿足的必要相似條件：

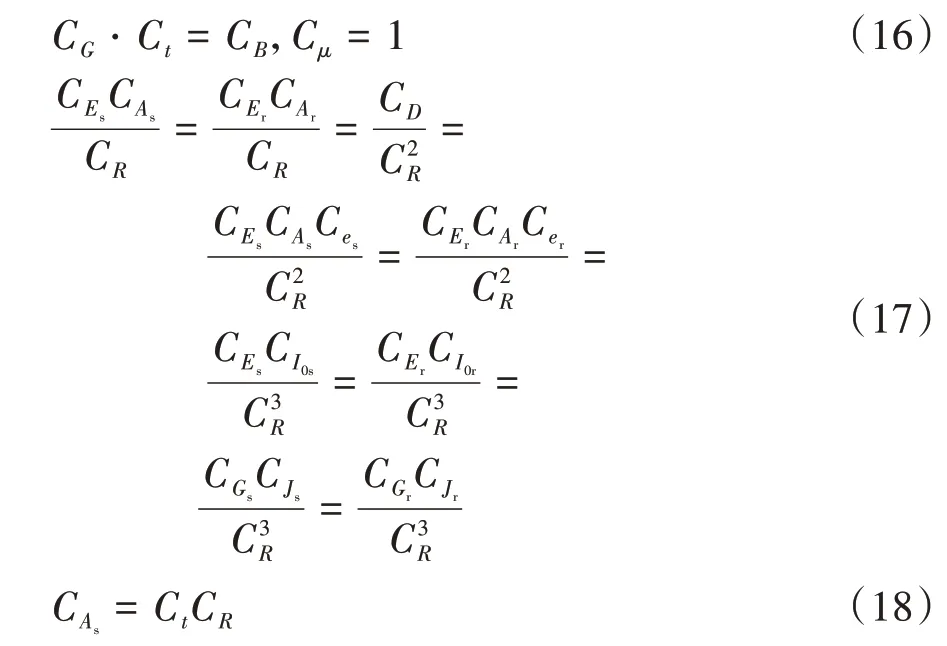
為了能準確預測原型結構的屈曲特性，原型與模型的屈曲模態相似條件為：

式中：m和n分別表示圓柱殼縱向和環向的波數.

1.2 縱環離散加筋圓柱殼軸壓后屈曲的縮尺原理公式

當加筋圓柱殼受軸向壓力px（受壓為正）時，根據廣義相似條件式（15），可以得到縱環離散加筋圓柱殼軸壓后屈曲相似不變量：

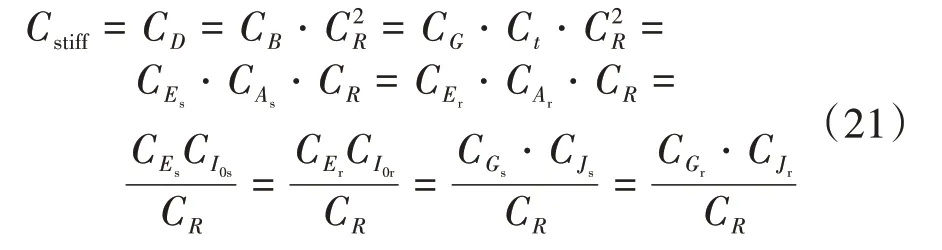
基于式（20），推導得縱環離散加筋圓柱殼軸壓后屈曲縮尺原理公式為：

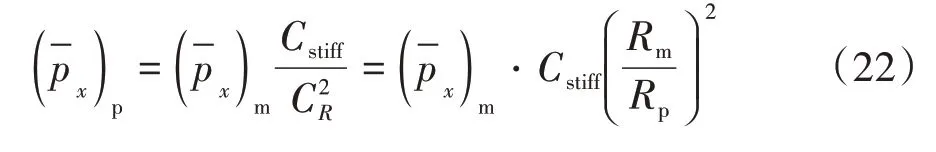
2 算例驗證

基于現有文獻中的模型，建立相同參數的有限元模型進行屈曲分析，并對比它們的屈曲荷載間的誤差，有效驗證了建立的含初始缺陷的光滑圓柱殼有限元模型的準確性.基于ANSYS 軟件建立有限元模型，模型采用shell181 單元，該單元為四節點六自由度單元，計算時間短，精度高.

2.1 含酒窩缺陷光滑圓柱殼軸壓后屈曲驗證

采用文獻［15］中含酒窩缺陷光滑圓柱殼軸壓后屈曲的算例進行有限元模型驗證.結構上端面承受軸壓荷載，下端面固支，上端面僅放松軸向位移自由度.材料和幾何參數為：E=72 GPa、μ=0.31、R=0.25 m、L=0.51 m 和t=0.000 5 m.在結構高度方向L∕2位置施加酒窩缺陷，缺陷函數［15］見式（23）.

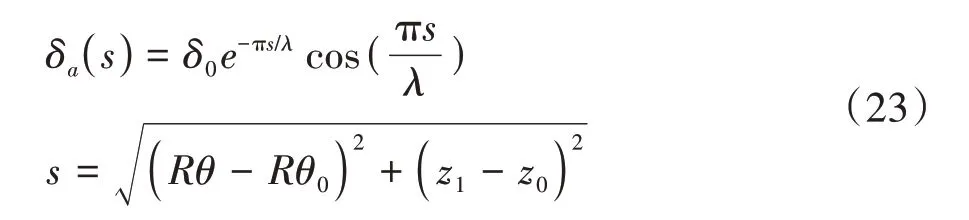
式中：s為缺陷范圍內有限元網格節點到缺陷中心的距離；λ和δ0分別為酒窩缺陷的直徑與中心幅值；θ和z1分別為光滑圓柱殼的環向和軸向的坐標；θ0和z0分別為酒窩缺陷中心的環向和軸向的坐標.

表1 給出含酒窩缺陷光滑圓柱殼軸壓后屈曲臨界荷載對比，其中pcr_α表示文獻［15］的臨界屈曲荷載，pcr_FEM表示本文計算的臨界屈曲荷載.由結果可知，不同缺陷半徑和不同缺陷幅值工況下，光滑圓柱殼軸壓屈曲臨界荷載與文獻［15］結果的誤差絕對值均小于8%，表明進行的含酒窩缺陷圓柱殼軸壓后屈曲分析準確、可靠.

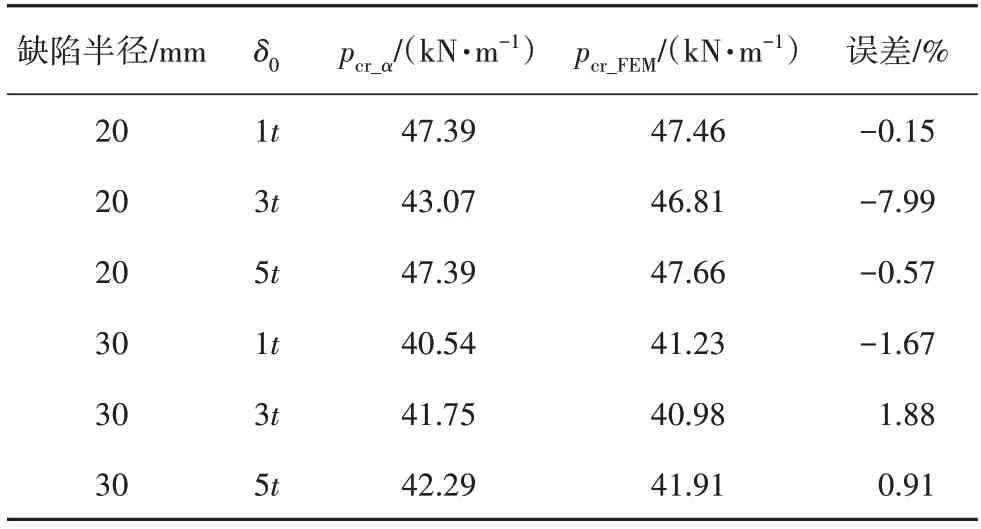
表1 含酒窩缺陷光滑圓柱殼軸壓后屈曲臨界荷載對比Tab.1 Comparisons of the buckling results the shells under axial compression with dimple imperfection

2.2 含環向焊縫缺陷光滑圓柱殼軸壓后屈曲驗證

采用文獻［16］中的含環向焊縫缺陷光滑圓柱殼軸壓后屈曲的算例進行有限元模型驗證.結構兩端面承受軸壓荷載，上、下端面簡支.材料和幾何參數為：E=200 GPa、μ=0.3、R=10 m、L=30 m 和t=0.001 m.在結構高度方向L∕2位置施加一條環向內陷焊縫，缺陷函數［16］見式（24）.

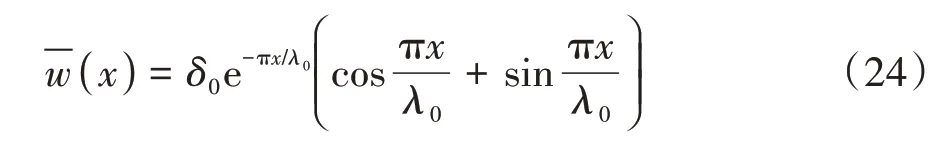
式中：λ0為焊縫缺陷半波長.

表2 給出含環向焊縫缺陷光滑圓柱殼軸壓后屈曲臨界荷載對比，其中pcr_β表示文獻［16］的臨界屈曲荷載.

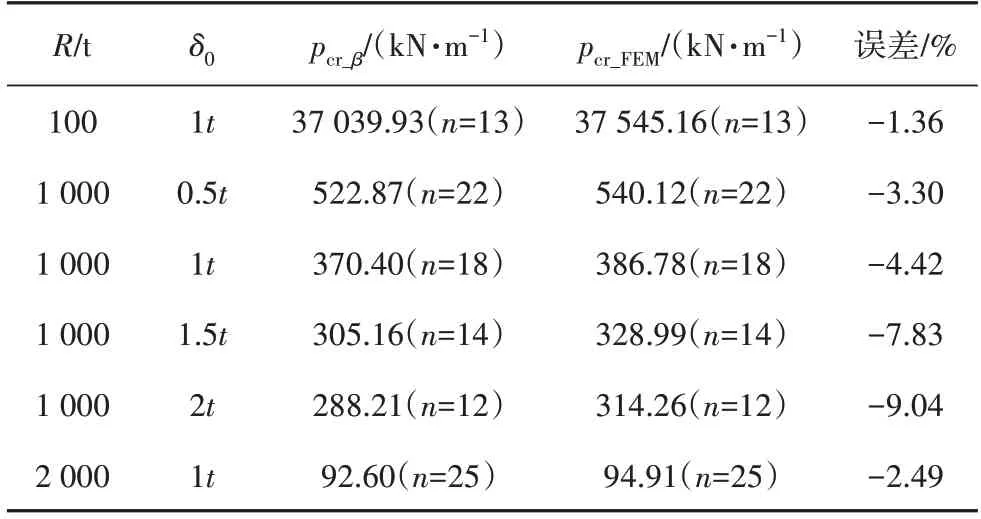
表2 含環向焊縫缺陷光滑圓柱殼軸壓后屈曲臨界荷載對比Tab.2 Comparisons of the buckling results the shells under axial compression with weld depressions

從表2 可以看出，不同徑厚比和環向焊縫不同缺陷幅值工況下的光滑圓柱殼，其軸壓后屈曲臨界荷載與文獻［16］結果間的誤差絕對值小于10%.同時，屈曲臨界荷載處相應結構的屈曲模態環向波數相同.缺陷幅值小于等于1.0t時，誤差絕對值在5%以內；當缺陷幅值為1.5t和2t時，誤差分別為-7.83%和-9.04%，誤差較大的原因可能是現有的板殼后屈曲分析理論尚不能較好地分析板殼結構缺陷幅值大于1.0t的情況.綜上所述，開展的含環向焊縫缺陷光滑圓柱殼軸壓后屈曲分析具有較好的準確性.

3 縱環離散加筋圓柱殼軸壓后屈曲不完全相似分析

為了驗證所推導的縮尺原理公式的準確性，首先對縱環加筋圓柱殼縮尺模型和原型進行軸壓后屈曲分析.其次，將縮尺模型的計算結果代入縮尺原理公式得到原型的預測結果.最后，將預測原型與原型的荷載位移曲線進行對比，并判斷它們的屈曲臨界荷載對應的模態是否一致.

縱環加筋圓柱殼原型結構上、下端面簡支.蒙皮與加筋肋的材料參數為：E=200 GPa、μ=0.3.加筋肋數量為：Ns=8、Nr=2.蒙皮與加筋肋幾何參數分別見表3和表4.

表3 蒙皮幾何參數Tab.3 Geometry parameters of the skin m

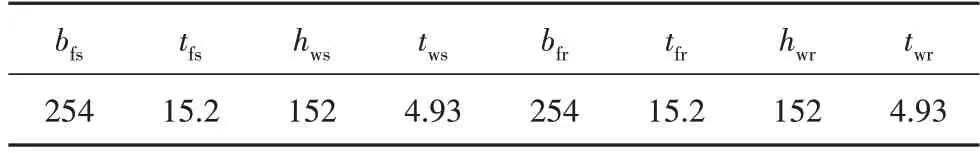
表4 加筋肋幾何參數Tab.4 Geometry parameters of the stiffeners mm

因滿足全部相似條件極其困難，且完全相似在實際情況中也不適用，故可忽略完全相似的部分非重要相似條件，進行結構的不完全相似研究.通過放松廣義相似條件，開展縮尺模型的材料和幾何尺寸均發生變化的不完全相似研究.此時，假設模型的蒙皮幾何尺寸具有相同的幾何縮尺因子，且模型與原型具有相同的邊界條件，可得如下相似關系：

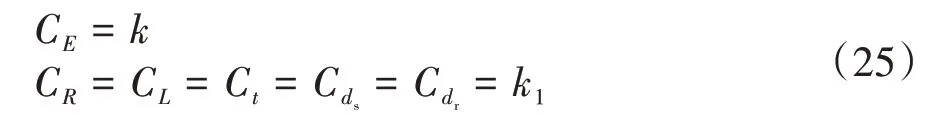
將式（25）代入廣義相似條件式（15）可得：

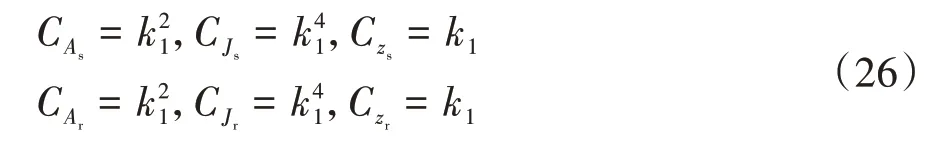
縮尺原理公式（22）可簡化為：

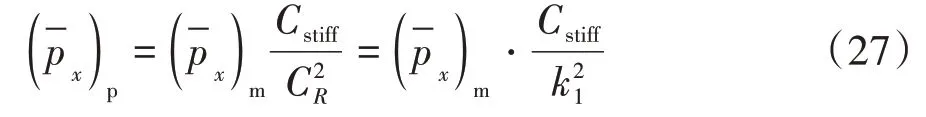
此時令Cstiff=CD，式（27）可進一步簡化為：

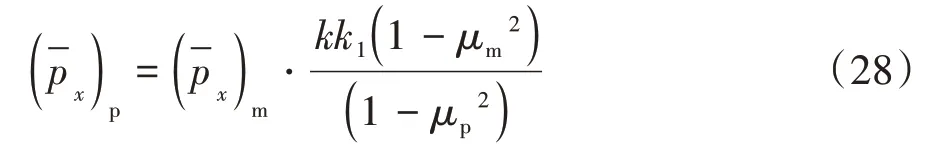
不完全相似縮尺模型的蒙皮幾何參數的縮尺因子均取10，同時，縮尺模型的蒙皮和加筋肋的材料分別使用鋁（Al）、紫銅（Copper）、黃銅（Brass）和塑料（PVC），表5 列出了縮尺模型的材料參數.根據式（26）求得縮尺模型環向和縱向等效加筋肋的幾何尺寸，發現它們的幾何縮尺因子與蒙皮的幾何縮尺因子相等.

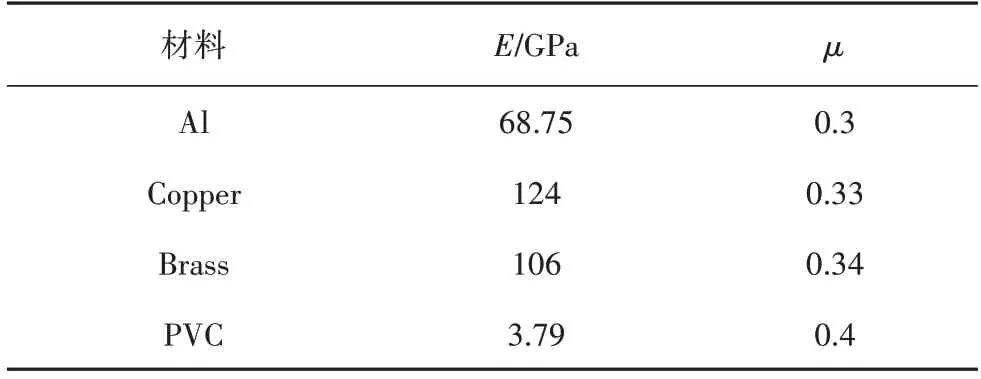
表5 不完全相似縮尺模型材料參數表Tab.5 Material parameters of the partly similar scale models

實際工程中的薄殼結構通常存在著一定的初始幾何缺陷.其中，酒窩缺陷與焊縫缺陷為典型且不利缺陷.因此，引入不同幅值的酒窩缺陷與環向焊縫缺陷，進行含初始缺陷的縱環離散加筋圓柱殼軸壓后屈曲不完全相似分析.

3.1 含酒窩缺陷縱環離散加筋圓柱殼軸壓后屈曲不完全相似分析

采用式（23）建立含酒窩缺陷的縱環加筋圓柱殼原型與縮尺模型.其中，缺陷幅值取δ0=IF·t，IF 代表初始幾何缺陷的缺陷因子，在結構環向加筋肋上施加2個酒窩缺陷，結構變形圖如圖3所示.

圖3 含酒窩缺陷T型縱環加筋圓柱殼結構變形圖Fig.3 Structural deformation diagram of the ring and stringer T-shaped stiffened-cylindrical shell with dimple imperfection

4 種不同模型材料的T 形縱環加筋圓柱殼軸壓后屈曲不完全相似模擬的結果見圖4～圖7.由圖可知，在結構達到屈曲前，其荷載與位移處于近似線性關系；當荷載達到上臨界點時，荷載隨位移陡然下降，結構進入后屈曲階段；同時，隨著IF值的增大，結構上臨界點對應的屈曲荷載逐漸減小.表6 為預測原型與原型的上臨界屈曲荷載的誤差對比.由表6可知，隨著模型與原型所取材料泊松比偏差的增大，預測原型與原型的上臨界點屈曲荷載的偏差也逐漸增大.IF=1，模型材料為Al 時，T 型縱環加筋圓柱殼平衡路徑上臨界點徑向位移矢量和云圖對比見圖8.通過對比上臨界點處屈曲模態圖可知，上臨界點處縮尺模型與其對應原型的屈曲模態均相同.由以上分析可知，基于縮尺原理公式，縮尺模型能較好地預測其對應原型的平衡路徑和屈曲模態.

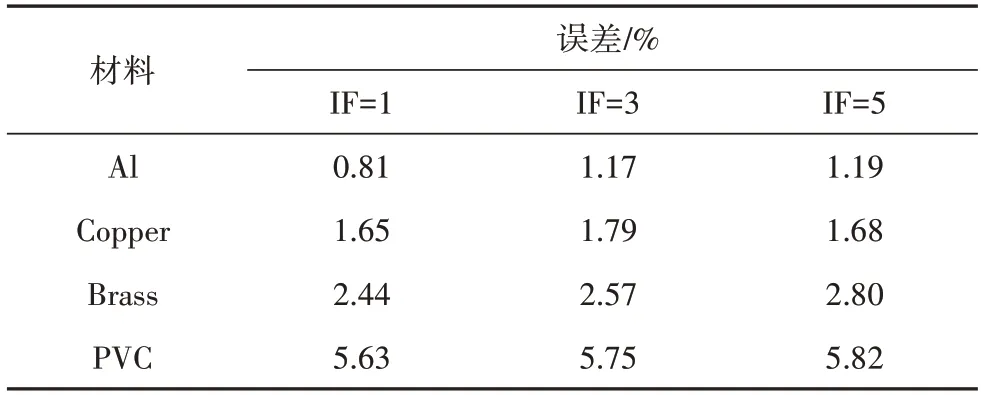
表6 預測原型與原型上臨界屈曲荷載的誤差對比Tab.6 Comparisons of the buckling results between the prototype and the predicted prototypes at the upper critical point of the post-buckling path

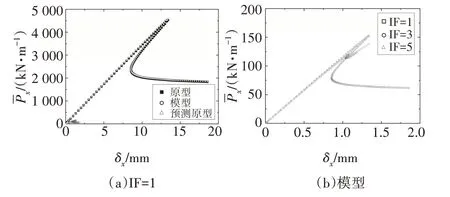
圖4 模型材料為Al時，T型縱環加筋圓柱殼軸壓后屈曲不完全相似模擬Fig.4 Comparisons between the predicted and original the load vs.end-shortening curves of the T-shaped stiffened-cylindrical shell under axial compression when the material is Al

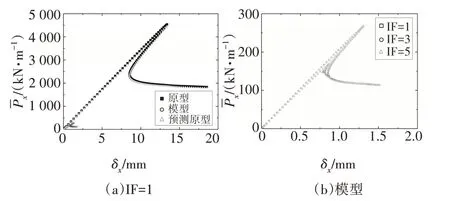
圖5 模型材料為Copper時，T型縱環加筋圓柱殼軸壓后屈曲不完全相似模擬Fig.5 Comparisons between the predicted and original the load vs.end-shortening curves of the T-shaped stiffened-cylindrical shell under axial compression when the material is Copper

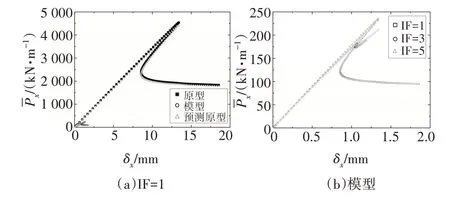
圖6 模型材料為Brass時，T型縱環加筋圓柱殼軸壓后屈曲不完全相似模擬Fig.6 Comparisons between the predicted and original the load vs.end-shortening curves of the T-shaped stiffened-cylindrical shell under axial compression when the material is Brass

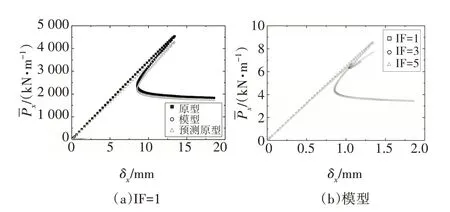
圖7 模型材料為PVC時，T型縱環加筋圓柱殼軸壓后屈曲不完全相似模擬Fig.7 Comparisons between the predicted and original the load vs.end-shortening curves of the T-shaped stiffened-cylindrical shell under axial compression when the material of the model is PVC

圖8 IF=1和模型材料為Al時，T型縱環加筋圓柱殼平衡路徑上臨界點徑向位移矢量和云圖對比（放大10倍）Fig.8 The radial displacement contour map at the upper critical point of the post-buckling path for the T-shaped stiffened-cylindrical shell when the material is Al and IF=1（magnified 10 times）

3.2 含環向焊縫缺陷縱環離散加筋圓柱殼軸壓后屈曲不完全相似分析

采用式（24）建立含環向焊縫缺陷的縱環加筋圓柱殼原型與縮尺模型，其中缺陷幅值取δ0=IF·（t+bf+hw）.在結構每條環向加筋肋翼緣的兩端上施加2 條環向焊縫缺陷，結構變形圖見圖9.

圖9 含環向焊縫缺陷的T型縱環加筋圓柱殼結構變形圖Fig.9 Structural deformation diagram of the ring and stringer T-shaped stiffened-cylindrical shell with weld depressions

4 種不同模型材料的T 型縱環加筋圓柱殼軸壓后屈曲不完全相似模擬的結果見圖10～圖13.由圖可知，結構達到屈曲前，荷載與位移處于近似線性關系；當荷載達到上臨界點時，荷載隨位移陡然下降，結構進入后屈曲階段；同時，隨著IF 值的增大，結構上臨界點所對應的屈曲荷載逐漸減小.表7 為預測原型與原型的上臨界屈曲荷載的誤差對比.由表7可知，隨著模型與原型所取材料的泊松比偏差的增大，預測原型與原型的上臨界點屈曲荷載的偏差也逐漸增大.IF=0.1，模型材料為Al時，T型縱環加筋圓柱殼平衡路徑上臨界點徑向位移矢量和云圖對比見圖14.通過對比上臨界點處屈曲模態圖可知，上臨界點處縮尺模型與其對應原型的屈曲模態均相同.根據以上分析可知，基于縮尺原理公式，縮尺模型能較好地預測其對應原型的平衡路徑和屈曲模態.

圖14 IF=0.1和模型材料為Al時，T型縱環加筋圓柱殼平衡路徑上臨界點徑向位移矢量和云圖對比（放大10倍）Fig.14 The radial displacement contour map at the upper critical point of the post-buckling path for the T-shaped stiffened-cylindrical shell when the material is Al and IF=0.1（magnified 10 times）

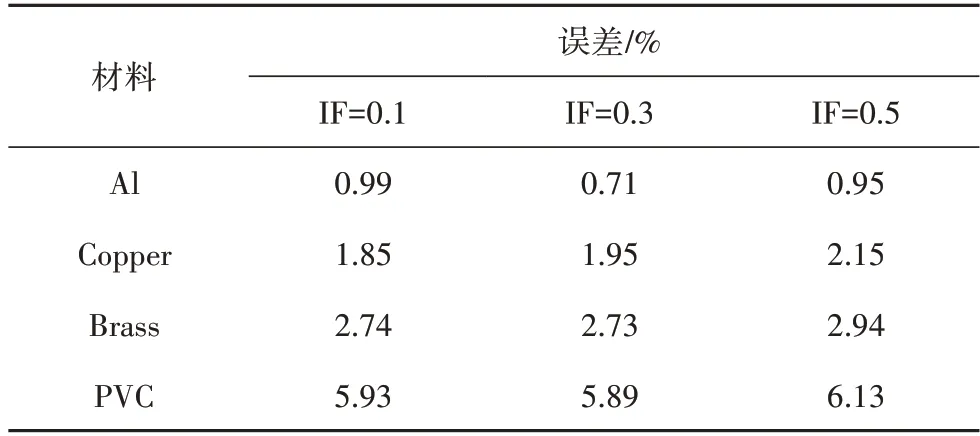
表7 預測原型與原型上臨界屈曲荷載的誤差對比Tab.7 Comparisons of the buckling results between the prototype and the predicted prototypes at the upper critical point of the post-buckling path

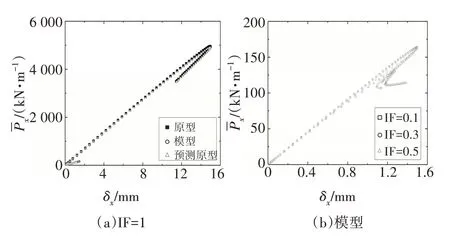
圖10 模型材料為Al時，T型縱環加筋圓柱殼軸壓后屈曲不完全相似模擬Fig.10 Comparisons between the predicted and original the load vs.end-shortening curves of the T-shaped stiffened-cylindrical shell under axial compression when the material is Al

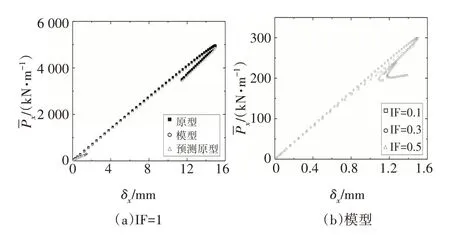
圖11 模型材料為Copper時，T型縱環加筋圓柱殼軸壓后屈曲不完全相似模擬Fig.11 Comparisons between the predicted and original the load vs.end-shortening curves of the T-shaped stiffened-cylindrical shell under axial compression when the material is Copper

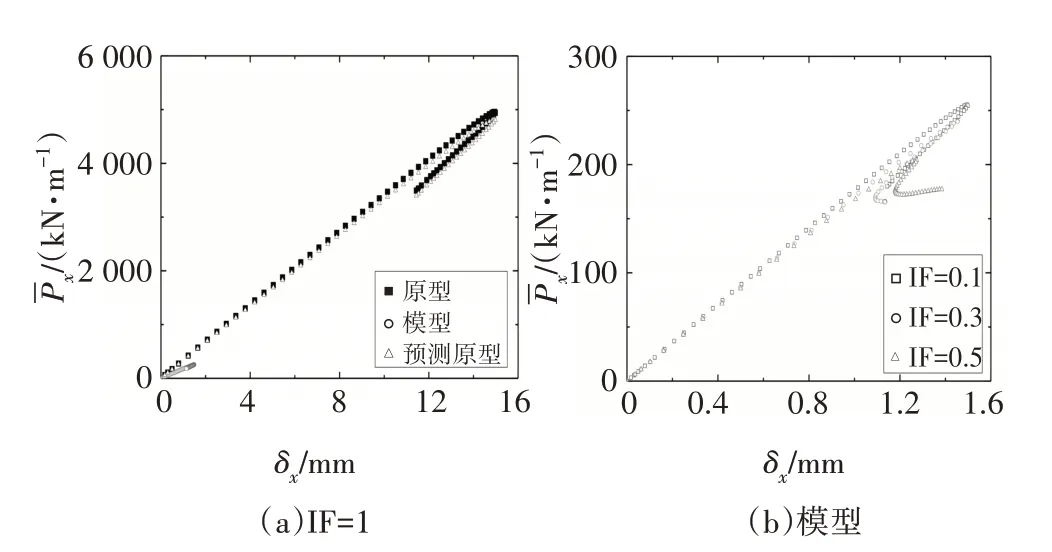
圖12 模型材料為Brass時，T型縱環加筋圓柱殼軸壓后屈曲不完全相似模擬Fig.12 Comparisons between the predicted and original the load vs.end-shortening curves of the T-shaped stiffened-cylindrical shell under axial compression when the material is Brassa

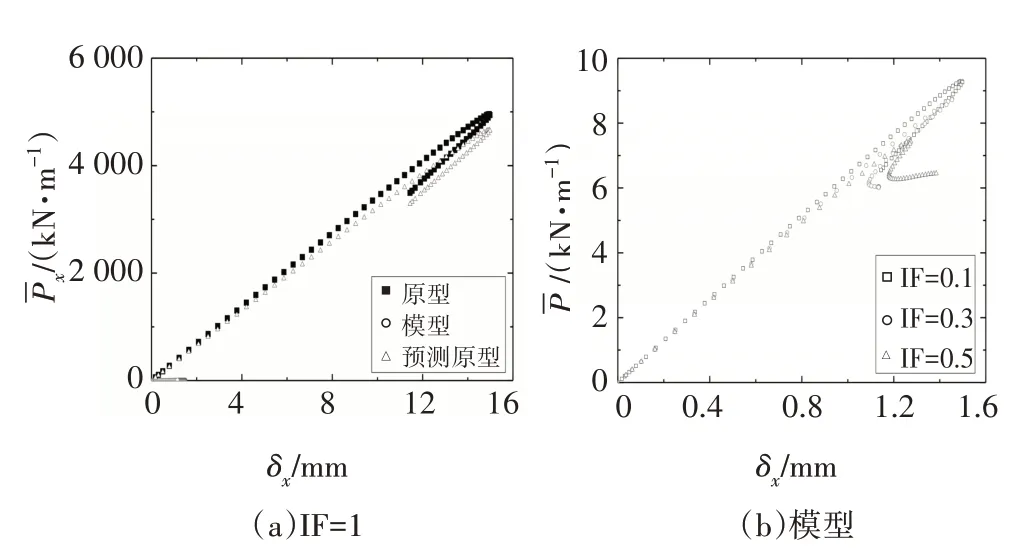
圖13 模型材料為PVC時，T型縱環加筋圓柱殼軸壓后屈曲不完全相似模擬Fig.13 Comparisons between the predicted and original the load vs.end-shortening curves of the T-shaped stiffened-cylindrical shell under axial compression when the material is PVC

4 結論

本文以縱環離散加筋圓柱殼為研究對象，根據離散加筋理論和能量法推導出結構軸壓后屈曲的廣義相似條件與縮尺原理公式；結合軸壓后屈曲縮尺原理公式，對含初始缺陷縱環加筋圓柱殼的原型和縮尺模型，進行了結構軸壓后屈曲的不完全相似分析.得到如下結論：

1）縱環離散加筋圓柱殼縮尺模型的軸壓后屈曲荷載位移曲線，結合結構軸壓后屈曲不完全相似縮尺原理公式，能較好預測原型結構軸壓后屈曲的結果.隨縮尺模型與原型的材料泊松比偏差的增大，由縱環離散加筋圓柱殼不完全相似縮尺模型預測的原型結構荷載位移曲線與原型結構結果的偏差逐漸增大.因此，在利用縱環離散加筋圓柱殼軸壓后屈曲不完全相似縮尺模型設計方法和縮尺原理公式進行相似預報時，模型結構與原型結構的材料泊松比應相近.

2）提出的縱環離散加筋圓柱殼軸壓后屈曲的縮尺模型設計方法和縮尺原理公式適用于不同幾何缺陷形式和缺陷幅值的加筋圓柱殼軸壓后屈曲相似預報，并且能比較準確地預報大型加筋圓柱殼軸壓后屈曲特性.這為采用離散加筋圓柱殼軸壓后屈曲縮尺模型實驗預測其對應原型的后屈曲特性提供了參考.