地下水位及地層滲透系數對基坑抗浮影響研究

陳昭陽，李 敏，高江林，趙一行，詹剛毅，石鈺鋒

（1.華東交通大學江西省巖土工程基礎設施安全與控制重點實驗室，江西 南昌 330013；2. 中鐵十八局集團第五工程有限公司，天津 300459；3 江西省水利科學院，江西 南昌 330029；4. 中鐵上海設計院集團有限公司，上海 200070）

近年來， 由地下水上升引起的基坑上浮事件屢見不鮮[1]，特別是針對超大、深基坑，處理不當將引起重大工程事故。 例如：南昌某學校綜合樓人防地下室上浮事故[2]；海口商場地下室上浮事故[3]；湖北保健酒基地工程聯合車間地下室上浮事件[4]等，造成很大財產損失及不良社會影響，故應對基坑上浮問題給予足夠重視。 萬先逵[5]等依托實際工程，探究基坑支護結構的優化方案。 董培鑫[6]等采用抗浮錨桿有效解決某中學操場抗浮問題。 張在明[7]對抗浮水位展開系統研究，提出將地下水位預測與孔隙水壓力分布用于抗浮水位分析中。 曹洪[8]等以本奈特假定為前提，推導出用于臨江二元地層滲流分析的簡化算法，得到強透水層中水頭分布，提出地下結構物底板的水壓力實用計算方法。 肖立[9]采用Plaxis 3D 軟件結合離心機模型試驗結果，研究得出儲罐側壁和地連墻受到的摩擦力對結構抗浮有重要的作用。 黃俊光等[10]提出主、被動抗浮措施的組合克服了傳統抗浮技術的不足。魯昂[11]針對設計中穩定安全系數、抗力分項系數等規范規定不統一的計算參數予以整理。 李國勝[12]認為設計中應根據當地的實際情況確定抗浮水位和不同抗浮水位時的抗浮驗算方法。 賈朋濤[13]認為場地地下結構抗浮水位取值考慮水的來源和排泄條件及建筑物的施工和使用兩個階段。劉子潔[14]、張竹庭[15]依托多個工程案例研究抗浮水位，認為地下結構抗浮水位由場地的水文條件、項目結構的具體功能要求及其他多種因素決定。 張國才[16]依據相關研究得出坡地地下結構的計算方法。 王帥[17]提出不同條件下基坑抗浮水頭取值的計算公式。 熊歡[18]提出位于砂土地層中的地下結構所受水浮力無需折減，而位于黏土地層中的地下結構所受水浮力應進行合理折減。 且由相關資料可知，基坑上浮緣于地下水浮力大于其自重、基坑內部荷載及周圍阻力總和，與地下水位高低、水位變化及地層滲透系數有關。 對于滲透系數較小地層應根據水頭損失程度對坑底水壓進行折減。

目前工程中常用抗浮措施有自重、加載、錨桿（索）、抗拔樁、排水減壓、隔滲帷幕抗浮[19-22]等。 本文主要考慮基坑在圍護結構自重作用下抗浮效果。 采用理論及數值計算手段對某超深圓形基坑自重抗浮進行驗算，分析依托工程水位變化后的抗浮穩定性，為抗浮措施決策提供依據。

1 工程概況

某盾構工作井為外徑35.9 m 圓形豎井。地面平整高程3.5 m，基坑底高程-63.85 m（不含集水井底坑加深2.5 m），開挖深度為67.35 m。采用地下連續墻+砼內襯墻支護方案。 基坑開挖采用地下連續墻垂直支護，盾構井內襯墻采用逆作法施工。 其支護結構設計為：地下連續墻厚1.2 m，嵌入井底4 m，逆作法內襯墻厚1.2～1.5 m，分界面于高程-18.25 m 處，采用C30 鋼筋混凝土。 襯砌后基坑內徑分別為31.1 m、30.5m。 洞門處設置兩道C35 砼環梁，寬×高為2.5 m×1.4 m。 如圖1 所示。 基坑降水井及監測點如圖2 所示， 其中LG09#-1-LD 表示垂直位移測點；LG09#-1-TP 表示水平與垂直共用測點；LG09#-1-IN 表示圍護結構頂部水平位移監測點；LG09#-1-UP 表示地下水壓監測點。

圖1 圓形基坑剖面圖（單位：mm）Fig.1 Profile of circular foundation pit（Unit：mm）

圖2 基坑降水井及監測點位布置圖（單位：mm）Fig.2 Layout of foundation pit dewatering well and monitoring points（Unit：mm）

該地區地下水豐富，以孔隙性潛水為主，地表水與地下水互為補排。 局部丘陵地帶以基巖裂隙水為主，大多在強風化泥質粉砂巖底部至弱風化泥質粉砂巖頂部。

施工前期地下水位于地下4 m 處，由于前期基坑施工時降水，引起周圍地層沉降，導致建筑物出現較大裂縫。 目前，基坑已施工完畢。 根據相關要求，現需將水位提升至原水位。 水位上升過程中，基坑中隧道開挖工作面出現滲水狀況。 為保證基坑及周圍建筑物安全，需對地下水位上升時基坑抗浮進行驗算。

2 數值分析

2.1 模型建立

采用Plaxis 3D 軟件對地下水滲流時基坑抗浮建模計算。 為消除尺寸效應，取模型尺寸X、Y 方向為基坑半徑5.5 倍 （即100 m），Z 方向為90 m。土層共8 層，從上往下依次為：人工填土、含淤泥質粉細砂、淤泥質黏土、含有機質粉質黏土、泥質細砂、強風化泥質粉砂巖、弱風化泥質粉砂巖。 基坑底部建立降水井。 地下連續墻及內襯墻按實際尺寸建立，并進行網格加密處理，模型底部及側面約束位移，如圖3 所示。 本模型僅考慮在圍護結構自重作用下基坑的抗浮能力， 忽略墻體與地層之間的摩擦作用。

圖3 有限元計算模型圖Fig3 Finite element calculation model diagram

2.2 參數選取

因本模型主要分析基坑抗浮，故模型各土層采用摩爾—庫倫材料模型，各結構均采用實體單元模擬。土層及結構參數根據相關地勘資料得出，如表1所示。

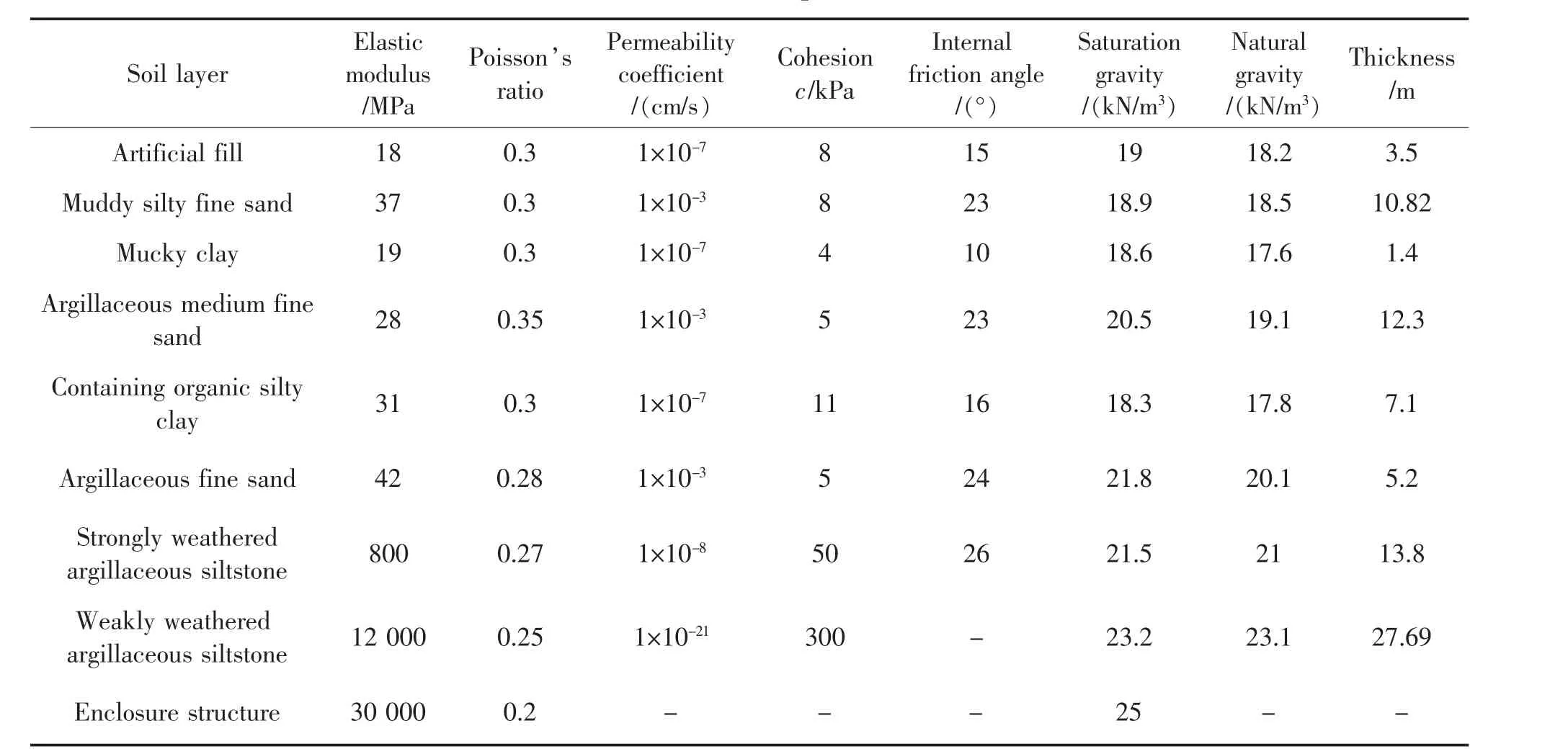
表1 計算參數Tab.1 Calculation parameters

2.3 模型正確性驗證

基坑開挖通過Plaxis 3D 中對某層土體的停用實現，地下連續墻及內襯墻施工通過啟用及改變材料屬性實現。 以下各步驟均在地下水滲流情況下進行，且除步驟1），步驟5）外，降水井均持續降水。 具體計算步驟如下：

1） 地應力平衡計算（即軟件中重力加載計算）；

2） 地下連續墻施工；

3） 模擬基坑開挖及施做內襯墻，根據現場實際施工進度，建立施工步驟；

4） 模擬基坑底板施工，該步驟完成后執行位移清零；

5） 降水井停止降水，地下水位回升至-6 m。

現場對基坑底部設置水壓預警值為0.2 MPa，由監測與模型計算數據對比可知， 如表2 所示，現場監測數值與模型計算數值吻合，表明該數值模擬合理。

表2 監測及數值計算數據對比值Tab.2 Comparison of monitoring and numerical calculation data

2.4 數值計算結果分析

為研究地下水位于原水位（-4 m）時基坑抗浮能力，將模型水位調整為-4 m。 計算得出基坑整體上浮位移為0.251 mm，基坑底部所受水壓為0.187 4 MPa，未超預警值。由此可知，該超深圓形基坑在圍護結構自重作用下抗浮效果較好。

3 力學計算

由于地下水滲流過程中，不同滲透系數的地層會使地下水產生水頭損失，故應按動水壓力計算

式中：qfw，k為構筑物基礎底面上的浮力標準值，kN/m3；γw為水的重度，kN/m3， 可按10 kN/m3采用；hw為地表水或地下水的最高水位至基礎底面 （不包括墊層）計算部位的距離，m；ηfw為浮力折減系數。

本文通過已驗證模型，計算當水位在-6，-7，-8，-9，-10 m 時基坑底部水壓值。 將數值計算及現場監測所得水壓與靜水壓比值作為該地層地下水浮力折減系數，如表3 所示。 由現場監測值計算得折減系數為0.293 8。 為滿足工程安全儲備需求，需選取表3 中折減系數的較大值。

表3 水壓折減系數Tab.3 Calculation parameters

取折減系數為

經計算得基坑圍護結構自重G自大于地下水浮力Ffw，且基坑以其自重可承受0.366 6 MPa 以內水壓。

4 地層滲透系數影響分析

基于上述數值計算模型，分析相同水位下地層滲透系數對超深圓形基坑圍護結構的影響。 以基坑圍護結構底板所在土層為界線（即-50.62 m 處），分別考慮上部土層及下部土層不同滲透系數對圍護結構的影響。 設置工況如下：

工況一： 當界線以下土層滲透系數不變時，上部土層整體增長0%、10%、20%、30%、40%、50%、60%時對基坑圍護結構的影響分析。

工況二： 當界線以上土層滲透系數不變時，下部土層整體增長0%、10%、20%、30%、40%、50%、60%時對基坑圍護結構的影響分析。

圖4～圖6 分別為工況一下基坑圍護結構水平位移曲線圖，圍護結構頂部沉降曲線圖及底部水壓曲線圖。

圖4 圍護結構水平位移曲線圖Fig.4 Horizontal displacement curve of retaining structure

由圖4 知：土層滲透系數增大10%時，對圍護結構水平位移影響影響較小；增大20%時，圍護結構水平位移值在-50.62 m 以上影響較大，平均增長率為7.3%，其中在-48 m 處增長率最大，為9%。-50.62 m 以下位移無變化； 增大30%時， 與增大20%時影響范圍相同。 平均增長率為9.5%，其中在-38 m 處增長率最大，為15.5%；增大40%時，影響范圍同上，平均增長率為19%，其中在-48 m 處增長率最大，為24%；增長50%、60%時對基坑圍護結構影響較小。

由圖5，圖6 知：土層滲透系數變化對基坑圍護結構頂部沉降及底部水壓影響較小。

圖5 圍護結構頂部沉降曲線圖Fig.5 Top settlement curve of retaining structure

圖6 基坑底部水壓曲線圖Fig.6 Water pressure curve at the bottom of foundation pit

綜上所述，上部土層滲透系數增長對圍護結構側面影響較大，對底部影響較小。

圖7， 圖8 分別為工況二下圍護結構頂部沉降曲線圖及底部水壓曲線圖。

據計算結果分析，界線以下土層滲透系數變化對基坑圍護結構整體的水平位移無影響。

由圖7 可知，界線以下土層滲透系數變化對基坑圍護結構頂部沉降值（即基坑上浮量）影響較大。土層滲透系數增大10%時， 圍護結構上浮量增加4.6%；增大20%時，上浮量增大8.8%；增大30%時，上浮量增大11.5%；增大40%時，上浮量增大13%；增大50%時，上浮量增大14.3%；增大60%時，上浮量增大15.3%。

圖7 圍護結構頂部沉降曲線圖Fig.7 Top settlement curve of retaining structure

由圖8 可知，界線以下土層滲透系數變化對基坑圍護結構底部水壓值影響較大。 土層滲透系數增大10%時，基坑底部水壓值增加0.96%；增大20%時，水壓值增大3.33%；增大30%時，水壓值增大5.87%；增大40%時，水壓值增大7.17%；增大50%時，水壓值增大7.39%；增大60%時，水壓值增大7.51%。

圖8 基坑底部水壓曲線圖Fig.8 Water pressure curve at the bottom of foundation pit

綜上所述，上部土層滲透系數變化對圍護結構側面影響較大，對底部影響較小。 下部土層滲透系數變化對圍護結構側面影響較小，對其圍護結構上浮量及底部水壓影響較大。

5 結論

本文依托某超深圓形基坑工程實例，采用理論及數值計算手段分析得出當水位回升至原水位時，有以下結論：

1） 在不考慮地層與基坑圍護結構間摩擦阻力的情況下，該超深圓形基坑可通過圍護結構自重抵抗地下水浮力，且有一定的安全儲備，現場施工可正常進行；

2） 該工程地層浮力折減系數約為0.3， 可供類似工程參考；

3） 基坑圍護結構周圍土層的滲透系數對其水平位移影響較大，對其沉降及底部水壓影響較小；

4） 基坑圍護結構底部所在土層的滲透系數對其沉降及底部水壓影響較大， 相對其周圍土層，底部土層滲透系數是影響圍護結構上浮的主要因素。