等式約束病態總體最小二乘的修正奇異值解及精度評定
翁 燁,邵德盛,2
(1.昆明理工大學 國土資源與工程學院,昆明 650093;2.云南省地震局,昆明 650200)
病態問題廣泛存在于自然科學和社會科學領域中,對于這些領域中的求解問題,常用Gauss-Markov模型或是離散動態模型進行建模,而最小二乘估計(Least Squares Estimate, LS)和卡爾曼(Kalman)濾波分別是兩種經典模型解算方法。測量系統的病態性通常表現為誤差方程系數矩陣具有復共線性[1],LS估計和Kalman濾波估計都存在估計方差膨脹導致參數估值不穩定的現象。自Gauss(高斯)提出最小二乘法開始,最小二乘估計理論在測量數據處理中得到廣泛的應用,最小二乘估計是測量平差的基礎方法,顧及觀測向量的隨機誤差,其平差準則是觀測向量的殘差平方和達到最小[2-3]。對于系數矩陣也存在誤差的函數模型通常稱為EIV(Errors-In-Variables)模型,則需要采用總體最小二乘估計(Total Least Squares, TLS),其平差準則是觀測向量和系數矩陣兩類殘差的平方和最小,平差理論更為合理[4-6]。對于EIV模型的解算研究,國外學者Gene提出在EIV模型下總體最小二乘問題的奇異值分解(Singular Value Decomposition,SVD)解法,推導出在系數矩陣的譜分解下參數的求和解式,缺陷在于并沒有消除或者削弱設計矩陣的病態性,只是對參數估計進行分開按照求和公式進行求解[4];Burkhard基于拉格朗日乘數法導出加權總體最小二乘的迭代求解公式,迭代計算過程復雜,計算量偏大,不利于編程實現[7],同時基于Gauss-Helemert模型,通過對非線性觀測方程中隨機誤差和待估參數進行線性化,由經典最小二乘法導出未知參數的迭代解式[8]。學者沈云中引入非線性最小二乘的Newton-Gauss法,導出加權總體最小二乘的迭代解式的同時還提出一種評定估值精度的數值算法[9]。
在大地測量和地球物理等領域的測量數據處理模型中,參數估計往往伴隨著先驗信息,此時傳統的參數估計問題即擴展為附有約束條件的參數估計,利用參數間一些精確已知的先驗等式約束信息也可以顯著提高解的準確性和精度,因此在病態總體最小二乘問題中,附加正確的等式約束也能夠提高其解的準確性和精度[10-11]。對于附有等式約束的EIV模型,國外學者Burkhard和Yaron研究了附有線性等式約束和二次型約束的等權總體最小二乘問題并基于拉格朗日乘數法導出參數的迭代計算公式[13-14]。但是,約束信息有可能會是相關的,約束方程就會出現病態,使得約束矩陣的微小擾動就會導致最終的反演結果產生極大變化,從而導致反演結果極不穩定,學者王樂洋等人討論了在具有病態性質約束矩陣的等式約束反演問題,并利用SVD方法來處理約束矩陣的病態性,有效解決約束矩陣病態造成的反演結果極不穩定的問題[15],同時還提出了在附有病態約束矩陣的等式約束反演問題的嶺估計解法,利用嶺參數來改變系數矩陣的病態性,提高參數解的可信度,使得反演效果良好,同時也帶有嶺估計統一改正的不足[16]。馬洋、歐吉坤等人驗證了降秩法與奇異值截斷法的基本等效性,針對附有病態約束的反演問題,提出了主模型與約束條件聯合解算的新方法,這種方法可以解決主模型病態甚至秩虧的問題,但丟失了部分原始成分信息[17]。為了保留先驗信息的完整性,文中在總體最小二乘平差準則的基礎上,考慮精確線性約束條件,利用修正奇異值法對病態設計矩陣的奇異值進行分區別修正,導出在精確約束條件下的病態總體最小二乘迭代解式,并進行參數估值的精度評定。
1 總體最小二乘的SVD模型
總體最小二乘的EIV模型為[5]:
L+el=(B+EB)X.
(1)
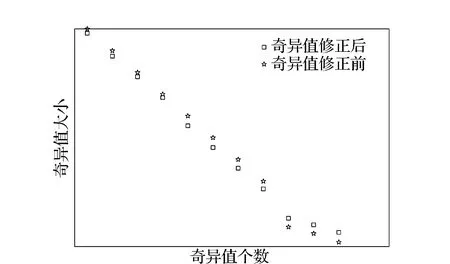
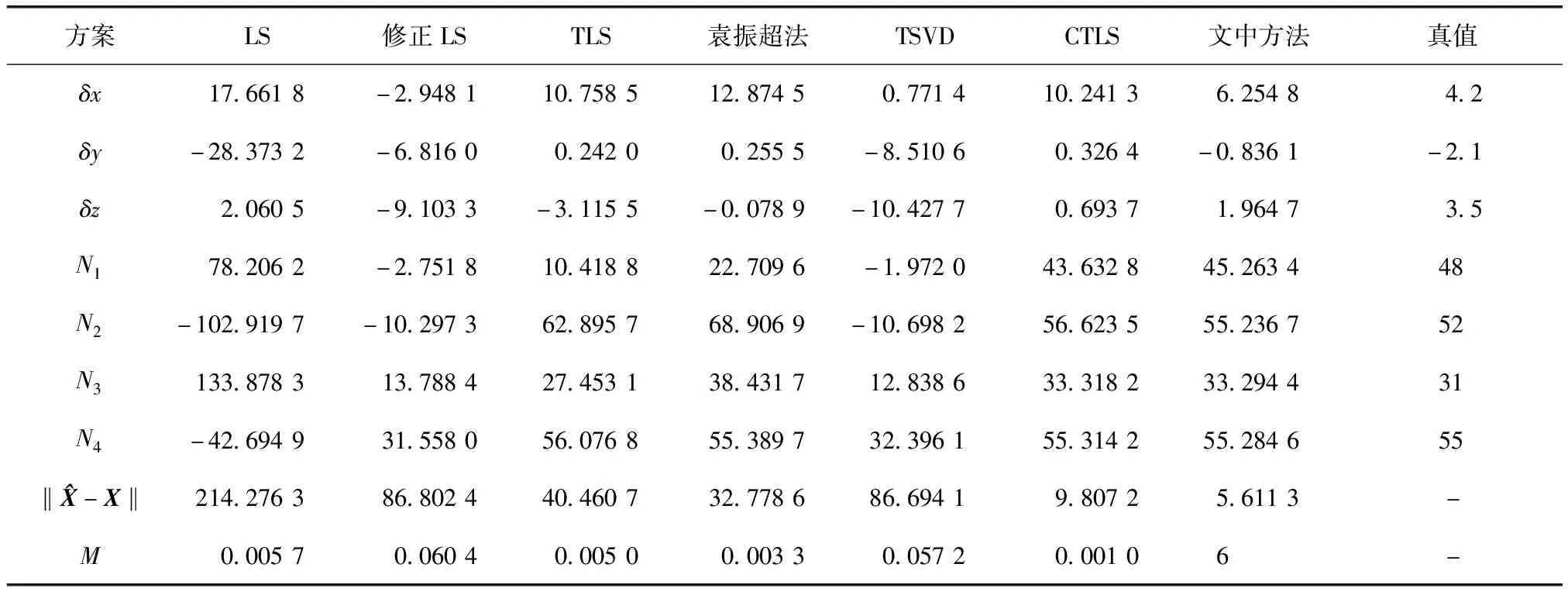
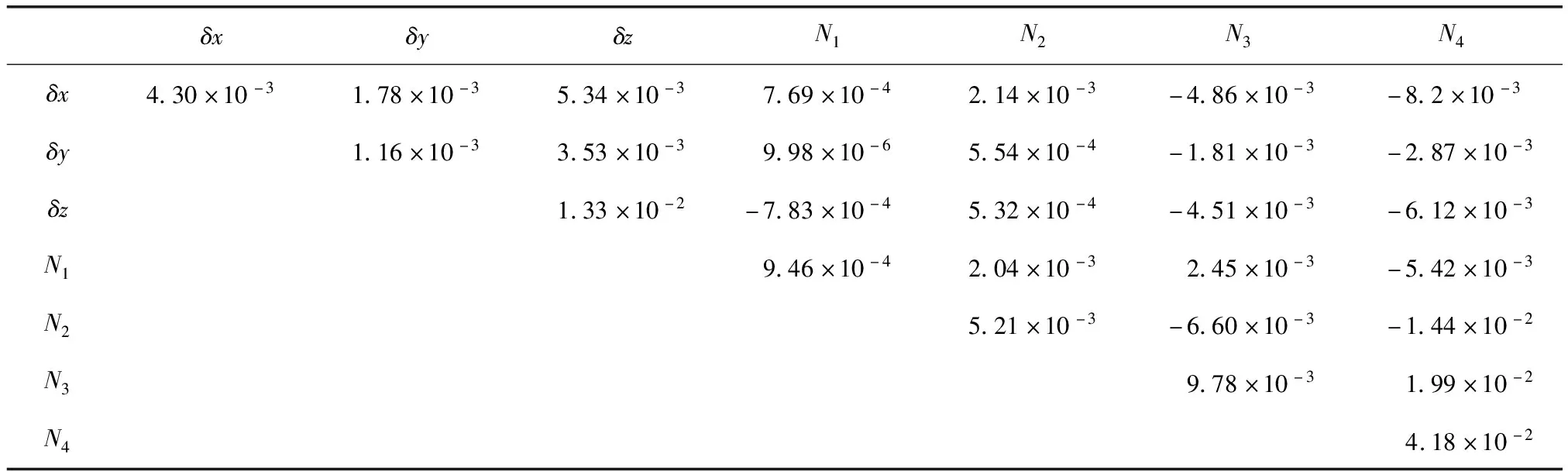
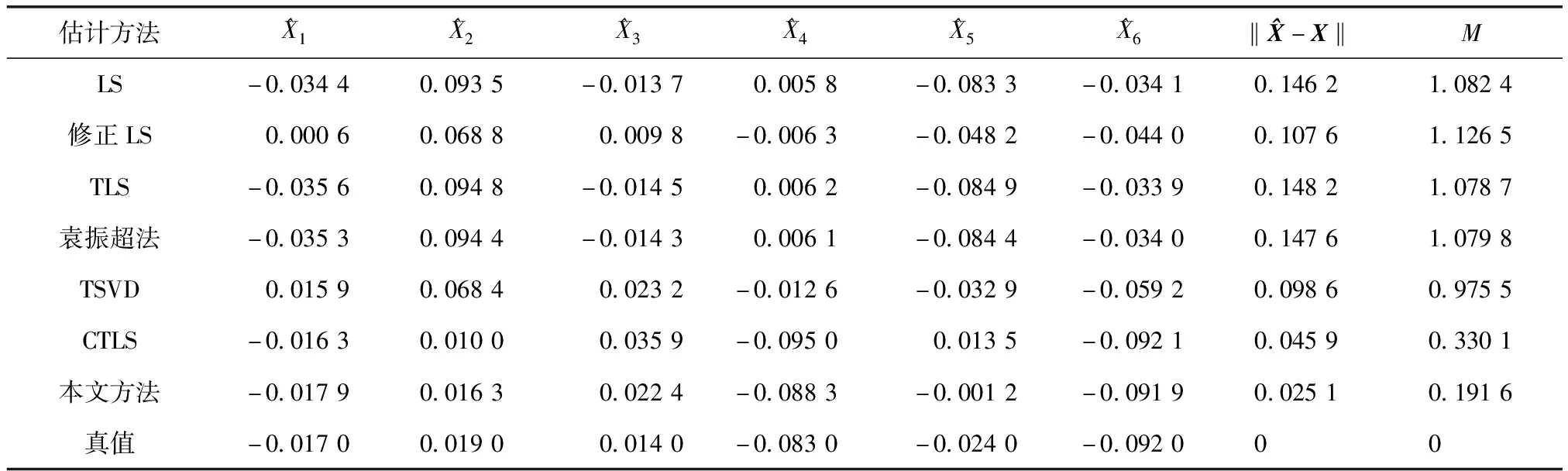
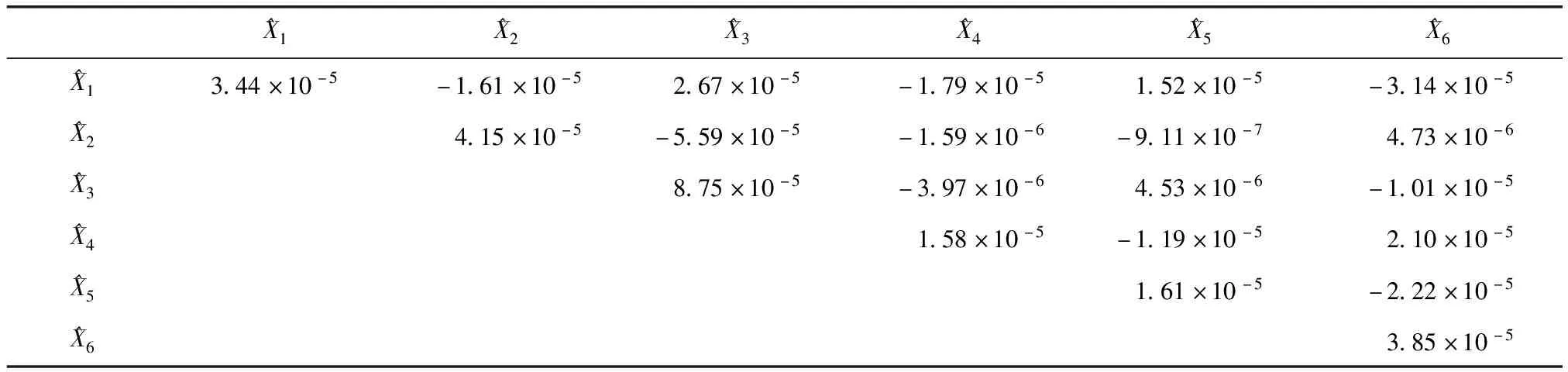
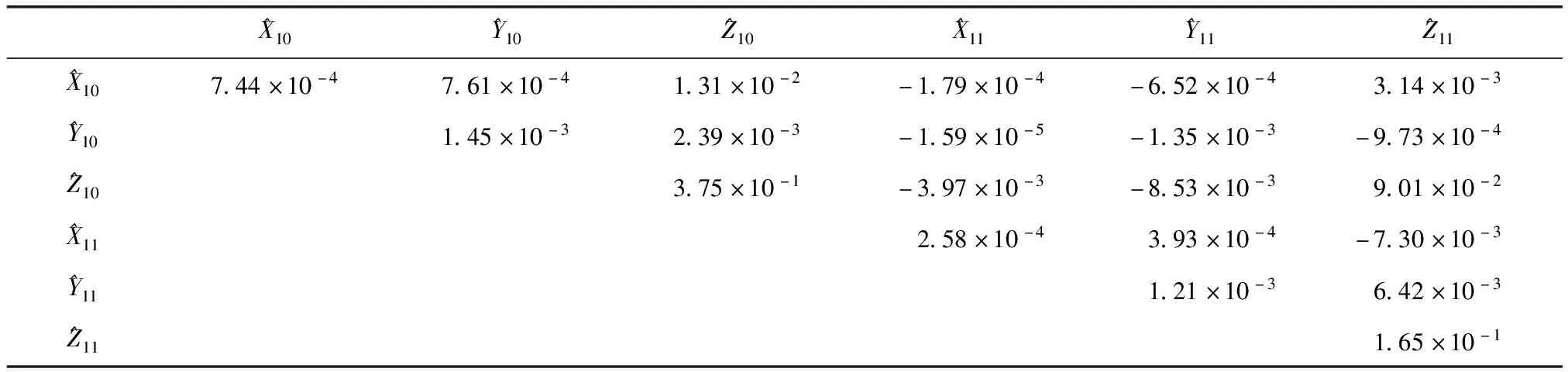
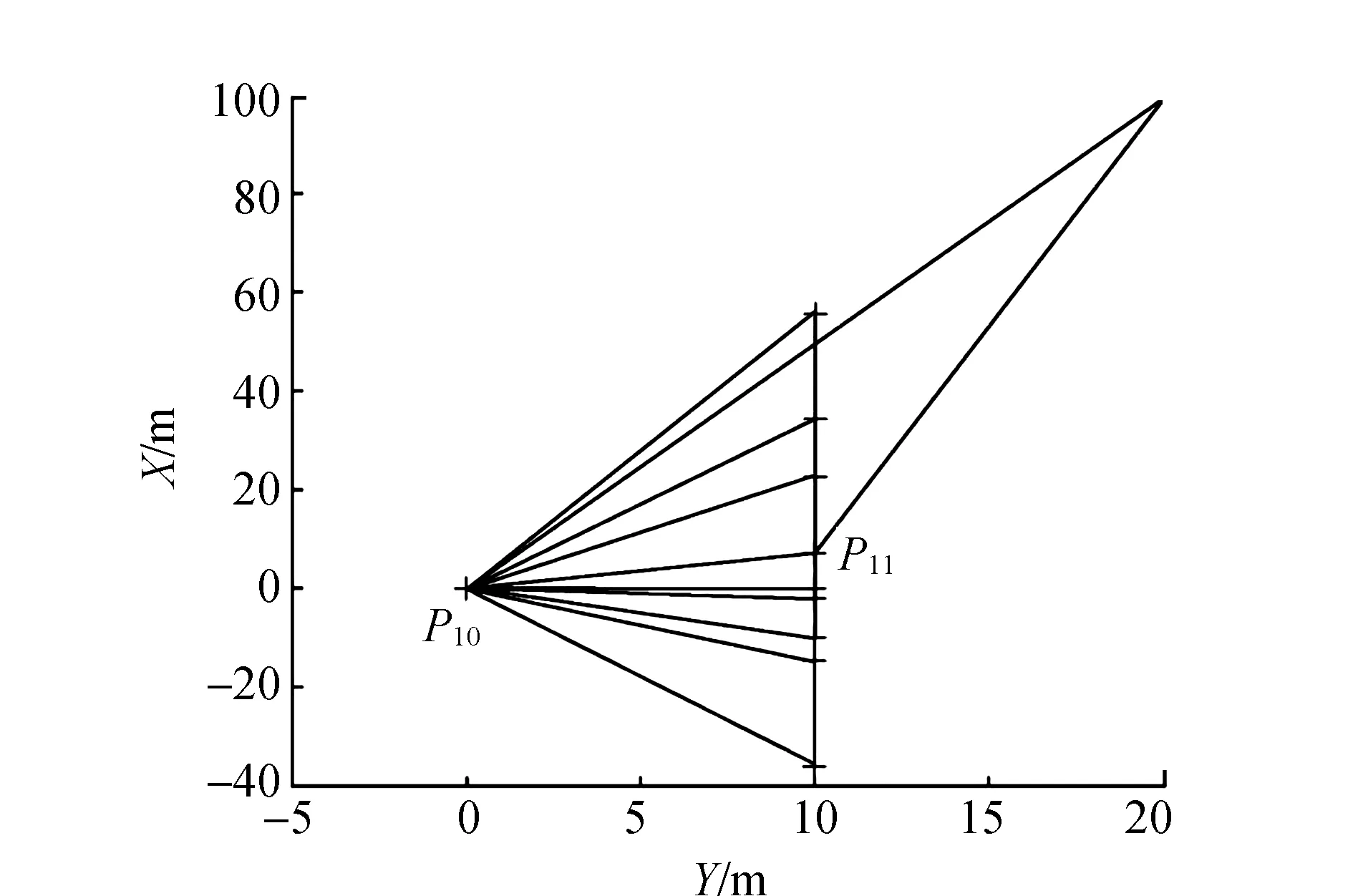
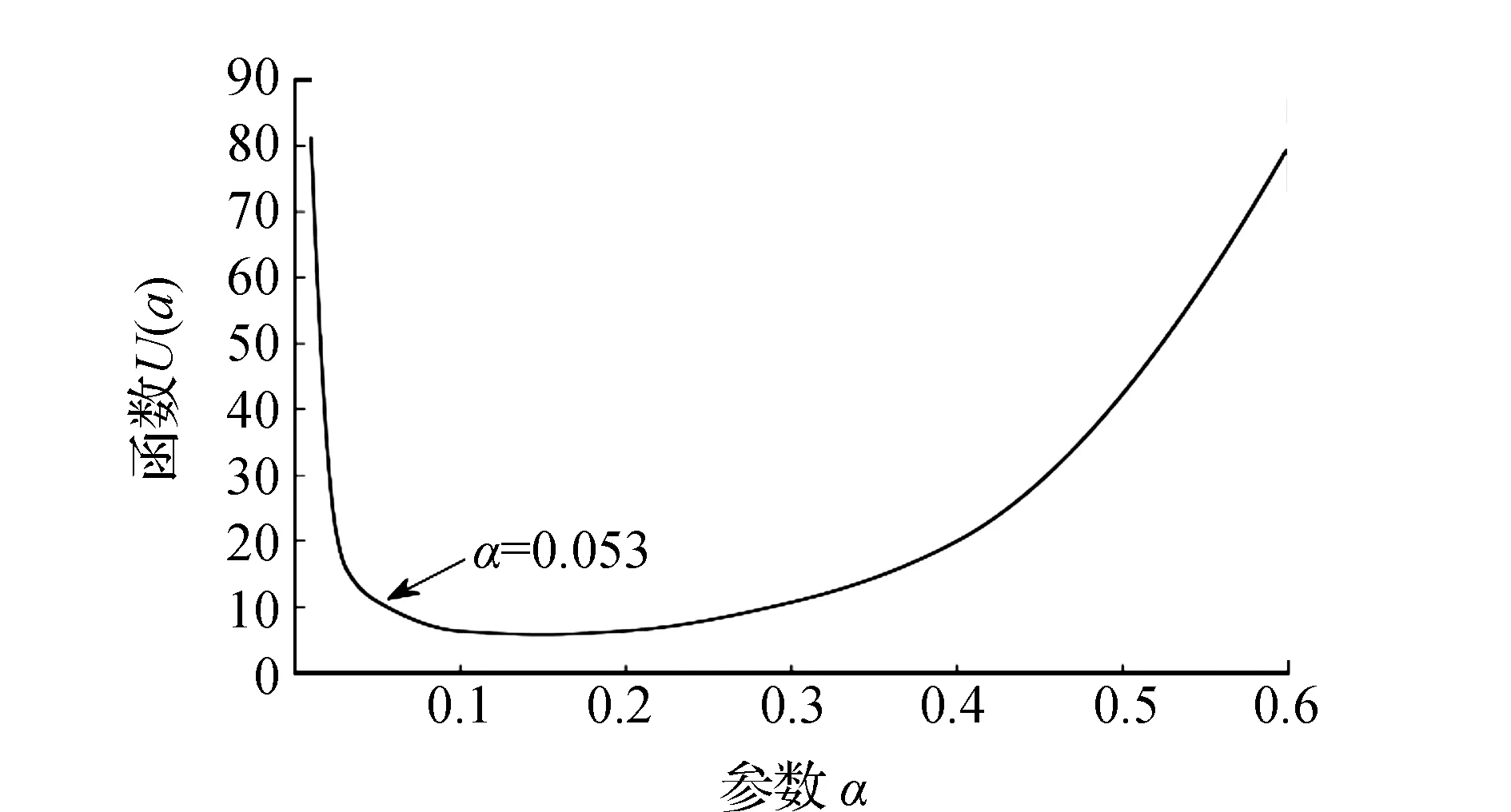
式中:L為觀測向量;B為設計矩陣且R(B)=m (2) 其中, eB=vec(EB), L=BX+e. (3) 根據總體最小二乘平差準則,模型(1)的求解式為: 在觀測向量和設計矩陣元素的權陣均為單位陣Pl=Im×n,PB=In×m時,求解式變為: (4) 當N=BTB病態情況不容樂觀,如在條件數rand(N)≥1 000時,最小二乘估計的參數值變得不可靠。為了參數估計值的穩定性,設法削弱法矩陣的病態性用以獲得穩定、可靠的法矩陣逆陣,采用截斷奇異值法來處理總體最小二乘估計。 將B矩陣進行奇異值分解,得到[15]: B=UΣVT. (5) 式中:U為n×m階矩陣;V為m×m階矩陣;均為正交矩陣。Σ為n×m階對角陣;對角元素為B的奇異值,按照降序排列,Σ=diag(λ1,λ2,…,λm)。將式(5)代入到LS參數估計中,并做譜展開有: (6) 式中:vi和ui分別是V和U的第i列向量;λi是B的第i個奇異值。通過式(6)看出在奇異值較小的時候,最小二乘估計解值被嚴重放大,截斷奇異值主要在于將小的奇異值截斷,避免了小奇異值對參數估計造成大的影響,若去掉后(n-k)個奇異值,則總體最小二乘的截斷奇異值解為: (7) 等式約束下的EIV病態模型為[4-6]: L+el=(B+EB)X, h=HX. (8) 式中:H為p×m階約束矩陣,h為p×1階約束常數項,且有rank(H=p (9) 其中,μ為p×1階拉格朗日因子,令 表示為: (10) 根據文獻[5]可知: (11) 組合式(10)、式(11)和式(8)可表示為: (12) 奇異值的修正要選取最小奇異值門限,設k為選取參數,將式(5)中的U,Σ,V進行矩陣分塊,得到: (13) 在進行奇異值分解后,相對較大的奇異值及其特征向量在參數模型解算中更可靠,相對較小的奇異值及其特征向量在解算過程中不太可靠。截斷奇異值法在于去除參數模型中的不太可靠部分,即刪掉相對較小的奇異值,從而減少解的方差,同時這會損害解的分辨率。若是奇異值呈現出如圖1所示的階梯狀時,截斷奇異值法比較適用參數估計,確定可靠成分和不可靠部分差別很大,截掉不可靠部分的奇異值對解的分辨率影響不大。Hansen從理論上證明了當奇異值分布呈現階梯狀時,截斷奇異值的方法與嶺估計的方法基本上是等價的。奇異值如圖1所示呈現的階梯狀且均勻分布,不可靠部分和確定成分的界限不好確定,難以確定截斷參數,建議采用奇異值修正法。 圖1 奇異值分類示意 奇異值的修正方法為:設t為截斷奇異值保留最小奇異值的門限,T為對應的小于t的奇異值個數,進行奇異值的修正[18]: (14) 修改后的奇異值變成 (15) 由于式(12)中系數矩陣和特征向量均存在未知估計參數,因此需要利用迭代法求解,求解過程如下: 2)根據式(12)得到: 其中,“:=”意思是“定義為”,將式(15)奇異值修正結果重新代入到模型式(6)中,再將LS估計值作為初始值參與迭代計算,迭代的次數就是修正奇異值參與的次數,就是病態精確約束總體最小二乘的修正奇異值解。 在病態方程中的法矩陣N的條件數大于1 000時,病態性較為嚴重,根據病態性情況結合條件數的定義[18]: (16) 在cond(N)2>1 000時,這里的范圍數可根據實際情況調整,即奇異值λk(k=1,2,…,n-1)滿足: 選取的奇異值最小門限為: t=λk. (17) 在精確約束條件下病態總體最小二乘的修正奇異值解的單位權方差為[5]: (18) 需要說明的是,由于在附有精確約束下的病態總體最小二乘問題中,未知參數的估計值采用的是迭代求解,未知參數與觀測向量無法分離,加上設計矩陣也是隨機矩陣,本身也存在誤差,因此在這種情況下的單位權方差無偏估計計算相對復雜,借助有偏殘差估計的單位權方差,即式(18)的單位權方差是有偏的。根據協方差的傳播率得出參數的協方差矩陣為: (19) 分塊矩陣形式為: (20) 采用GPS動態定位的解算,取歷元間隔時間為2 s,觀測了5顆衛星,用4個歷元解算整周模糊度,誤差方程的系數矩陣為[19]: (21) (22) 表1 不同方法參數估計結果比較 表2 參數估計值的方差-協方差陣 圖2 U曲線法確定正則化參數α 表3 真實坐標與近似坐標 m 表4 邊長觀測值(觀測向量和設計矩陣, 圖3 三角形網 圖4 U曲線法確定正則化參數α 表5 不同方法參數估計結果比較 表6 參數估計值的方差-協方差陣 表7 不同方法參數估計結果比較 表8 參數估計值的方差-協方差陣 圖5 空間測邊網的平面分布圖 圖6 U曲線法確定正則化參數 參數估計的精確度容易受到誤差方程的系數矩陣病態性影響,在病態性較為嚴重時,LS估計值近乎失真,其與真值的差值范數也較大;根據3個算例的計算結果得知,TLS在病態性較為嚴重時估計的結果也不理想,此時可以考慮總體最小二乘的截斷奇異值法或總體最小二乘的正則化法。CTLS方法比較依賴于等式約束條件的系數矩陣,同時又受到誤差方程系數矩陣的影響。修正奇異值法的直觀展現在于進行一次奇異值修正時,參數估計值與真值的差值范數為: 算例1: 算例2: 算例3: 進而使得參與迭代計算的初始值經過奇異值修正后有所改善。 參數估計的先驗信息能夠提高參數估計解的準確性和精度。在等式約束下,提出了病態總體最小二乘估計的修正奇異值解法,利用總體最小二乘準則和協方差傳播率推導出在等式約束下的總體最小二乘迭代式;并借助有偏殘差估計的單位權方差,通過協方差的傳播率得出參數的近似協方差矩陣。用數值分析算例和測邊網算例驗證文中方法,并與TSVD、TLS和CTLS等參數估計方法作比較,證明文中方法在奇異值按照降序排列且成階梯均勻分布時,用于對參數估計精度提升最有利,文中方法在于保持參數估計解的分辨率同時顧及解的精度提升。文中只做了在等式約束下總體最小二乘奇異值修正,后續將進一步研究在隨機約束、不等式約束下的總體最小二乘奇異值修正方法。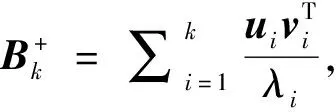
2 等式約束條件總體最小二乘模型
2.1 等式約束總體最小二乘的修正奇異值解
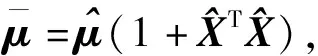
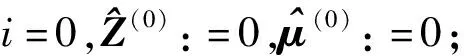
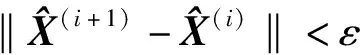
2.2 最小奇異值門限的確定
2.3 精度評定
3 算例及分析
3.1 整周模糊度算例
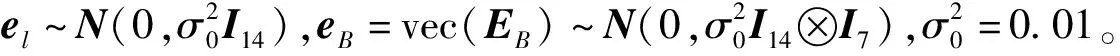
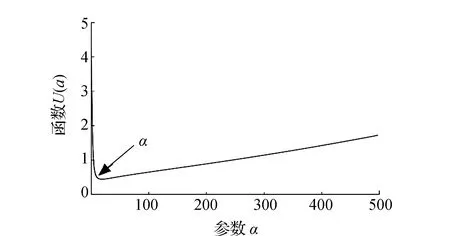
3.2 測邊網算例

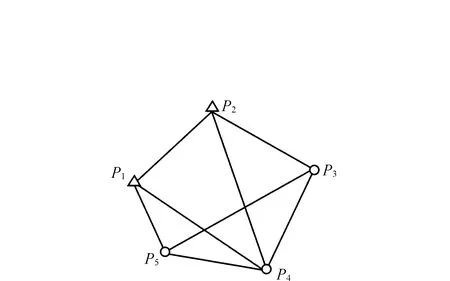

3.3 病態網算例
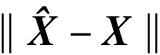
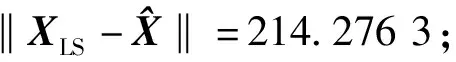
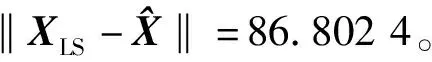
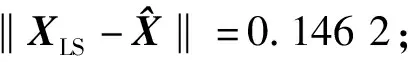
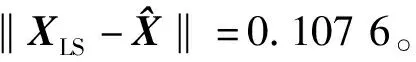
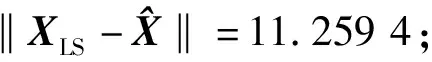
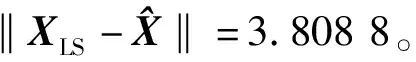
4 結束語

