天氣雷達三維回波實時渲染算法研究

王 興， 錢代麗， 朱 彬，， 安俊琳， 呂晶晶

（南京信息工程大學 a.大氣科學與環境氣象國家級實驗教學示范中心，b.大氣科學與氣象信息國家級虛擬仿真實驗教學中心，南京 210044）

0 引 言

曲面重建是對離散的空間數據進行三維渲染的主要技術手段，其基本思想是按照一組給定的閾值從三維點云數據中提取相應的等值面，利用曲面渲染算法生成一組由不同顏色相互疊加的等值面［5-6］。曲面重建的算法很多，主要可分為兩類：一是基于斷層輪廓線的表面重建，即將三維數據分割成若干個二維切面，分別計算各切面的等值線，再將這些等值線連接成等值曲面；二是基于體素的等值面重建，即對三維點云構成的體數據場中的各個體素加以分析，提取等值面信息，再將這些等值面連接成等值曲面［7-8］。其中，移動立方體法（Marching Cubes，MC）［9］是沿用至今且頗具影響力的體素等值面重建算法之一。

曲面重建技術在醫療、建筑等工程領域的研究最為深入，近年來，也有一些研究將該技術應用于天氣雷達、衛星和數值模式等資料，實現氣象數據的三維可視化交互［10-11］。由于雷達探測數據的空間分布極不規則，距離雷達近端與遠端的相鄰離散點之間，間隔距離相差超過100倍，在重構均勻三維格點場雷達回波時，傳統空間插值算法并不適用。雷達遠端的插值點不僅難以還原真實的探測值，還極大地增加了點云的密度，造成面片的計算規模陡增，網絡結構復雜化，大幅增加了三維渲染的時長，影響三維可視化的實時性和可交互性。

為解決上述技術難題，針對多普勒天氣雷達探測方式及其數據特征，在移動立方體算法基礎上，提出一系列改進，并對改進前、后的渲染效果做出比對分析。

1 基本原理與技術路線

1.1 移動立方體（MC）算法

MC算法最早是Lorensen等［9］提出，用于解決三維物體的面繪制問題。其本質是將三維坐標系下的物體分解為體素集合，每個體素包含8個空間上緊相鄰的頂點，構成一個正立方體，將該正立方體視為基本單位。曲面重建時，先設定一組大小不同的閾值，通過計算每個體素內的梯度變化，并與各個閾值分別進行比較，找出所有被閾值穿過的正立方體，再利用插值算法計算出這些表面（即等值面），再通過繪制一系列閾值的等值面，實現三維矢量圖像的繪制。

受制于20世紀80年代有限的計算機圖形處理能力，MC算法巧妙地利用三角面片近似表示待求取的等值面，極大地提升了計算效率。由于等值面與體素邊界面的交線是雙曲線，在特定情況下對相同的等值點可以采取不同的連接方式，這種近似表示的算法無法保證三角片所構成的等值面的拓撲一致性，造成很多三角面片銜接處出現孔隙和不連續現象。為克服這一問題，很多學者對MC算法提出了改進，有的是利用插值和雙曲漸近線將體素進一步拆分［12-13］，有的是將MC的正立方體進一步簡化，采用四面體剖分［14］等。

1.2 MC應用于雷達回波渲染的技術缺陷

氣象雷達探測得到的數據，其空間分布是一個不規則的三維點云結構，隨著探測距離的增加，點云愈發稀疏，距離雷達近端與遠端的相鄰離散點之間，間隔距離相差可達100倍以上。在重構均勻三維各點場雷達回波時，諸如雙線性插值、最近鄰插值、三次內插等傳統空間插值算法并不適用。

宴會中，馬老當場宣布，這次活動的成功舉辦，在座的各位功不可沒。公司將論功行賞，給予在座的各位同仁以物質獎勵，對公司的高管層將另行獎賞。獎勵田卓小姐、高潮先生赴巴厘島六日游，馮可兒小姐本來也在去巴厘島之列，但考慮到公司不可一日無主，就留下來代理田卓行使管理權，但公司會額外補償馮可兒小姐不能成行的損失。

盡管MC利用三角面片擬合曲面的算法設計非常巧妙，在曲面渲染時也表現出不錯的性能，但對于面片的生成，卻需要消耗“過多”的內存和計算時長。這主要是因為MC算法需要遍歷三維點云數據中的所有體素，而與等值面相交的體素數量僅占所有體素的1/10甚至更低。雷達探測的空間范圍大（數百公里），數據密度高，一次計算需要處理數百萬個體素，而近9成的時間被用于計算這些無效體素。雷達遠端的插值點不僅難以還原真實的探測值，還極大地增加了點云的密度，使得體素產生的面片面積過小，造成面片的計算規模陡增，網絡結構復雜化，大幅增加了三維渲染的時長，影響了三維回波渲染的實時性和可交互性。

1.3 雷達三維回波實時渲染算法流程

為克服上述不足，本算法以傳統MC算法為基礎，針對雷達基數據的空間結構特點，著重在三角面片頂點位置的計算、三角剖分構型唯一性的判定以及包含等值面體素的加速遍歷，這3方面提出修改和優化。雷達三維回波實時渲染的總體算法流程如圖1所示。

圖1 總體算法流程圖

2 雷達三維回波實時渲染算法

2.1 數據準備

國內常用的天氣雷達分為S波段、C波段和X波段3類，每個波段各有多種型號，每個型號的雷達又可采用多種方式的體掃模式。以我國東南沿海地區最常用的SA型為例，它的體掃模式主要有VCP11（Volume Coverage Pattern）、VCP21和VCP31這3種。其中，VCP21常被用于探測非強對流的明顯降水情況，該模式的體掃周期為6 min，方位角方向的分辨率為1°，徑向分辨率為0.25 km，探測距離為460 km［15］。1個體掃周期內完成9個不同仰角掃描，仰角與高度、水平距離的關系如圖2所示。

圖2 SA雷達VCP21體掃模式

圖2中：hd為水平距離；vh為垂直高度，單位均為km；ev為探測仰角，單位為（°）。通常情況下，MC算法分析的數據在空間上等間隔分布結構，即各個位置的體素密度相同。顯然，雷達探測數據結構并不滿足這一特征，通行的做法是將極坐標系下的數據結構通過空間插值轉換成平面直角坐標系下的三維結構，但額外增加的體素信息不能準確地反映大氣中的水氣狀況，除了方便計算，并不能帶來性能上的有益提升。本算法不做插值和坐標系轉換，而直接根據雷達探測所構成的數據空間結構，分析各個等值面閾值與基本反射率之間的數值關系。

如圖3所示，a～h為雷達探測可識別分辨率下某處相鄰的8個頂點，各頂點的數值為該位置探測到的基本反射率，用Z（λ，θ，φ）表示，單位為dBZ。這8個頂點構成一個六面體，將其視作一個體素，它是后續MC計算的基本單位。

圖3 極坐標系下相鄰8頂點的空間分布

2.2 極坐標系下三角面片頂點位置的計算

體素中的三角面片是擬合等值面的基本單位，要得到三角面片的空間位置，就需要準確計算等值面在體素棱邊相交點的坐標。通常在由X、Y、Z構成的空間直角坐標系下，可以利用線性插值計算各個交點的坐標。雷達數據是極坐標系下的空間三維結構，計算方法需做相應轉換。假設D1=（λ1，θ1，φ1）和D2=（λ2，θ2，φ2）是體素棱邊上兩個端點的坐標，閾值為T1的等值面在該棱邊上有交點，那么該交點的坐標P（λ，θ，φ）計算方法為：

2.3 基于相鄰體素狀態的快速判別算法

VCP21體掃模式類似圖3所示，由8個頂點構成的六面體（體素）約有1.32×106個，采用MC算法對所有體素逐一遍歷，將消耗大量時間，且大多數體素與待求取的等值面并不相交。為提升計算效率，采用一種區域拓撲擴展的思想，先任意選取一個與等值面相交的體素，將其作為基準，篩選出與該體素相鄰且包含等值面的體素，再分別將這些體素作為基準，采用相同方法擴展篩選，直到找出所有與等值面相交的體素，再做后續處理。

上述過程的關鍵是如何判別與基準體素相鄰的體素是否與等值面相交。如圖4所示，有4個相鄰的體素，每個體素包含8個頂點，其中CD是4個體素公有的邊，ABCD是上方2個體素公有的面。如果A、B、C、D4個頂點的基本反射率數值不全部小于或大于等值面的閾值，則可判定基準體素的相鄰體素與等值面相交。圖4中MN表示左上角的基準體素與等值面的交線，由于MN也存在于右上角的體素中，因此，右上角的體素也與等值面相交。

圖4 相鄰體素等值面與交線的示意圖

盡管A、B、C、D的取值不定，但相較于等值面的閾值，只有小于、大于或等于這3種狀態。為簡化表述，不妨假設當頂點的基本反射率數值小于或等于等值面的閾值時，設定為狀態“T”，當大于時設定為狀態“F”。那么，對于體素中任意一面的狀態可總結為如圖5所示的4種狀態。

圖5 體素中一個面與等值面相交的情況

圖5中，體素一個面的頂點用黑色實心圓和白色空心圓分別表示狀態“T”和“F”。其中，圖5（a）有1個頂點與其他頂點的狀態不同；圖5（b）、（c）各有2個頂點與其他頂點的狀態不同；圖5（d）中4個頂點為同一狀態。圖5中的虛線為體素的一個面與等值面相交的示意，相交的準確位置可采用2.2節所述方法計算得到。其他情況均可通過旋轉或翻轉圖形歸并到圖5所示的4種情況之一。在遍歷計算相鄰體素時，可借助哈希表輔助算法執行［16］。

2.4 體素中三角剖分構型的唯一性判定算法

傳統MC算法中，當狀態“T”和“F”的頂點如圖5（c）所示分別位于對角線的兩端，那么等值面與體素相交的方式會有兩種，因此存在歧義，如圖6所示。為保證三角面片拓撲結構的一致性，一些學者提出了子構型拆分和雙曲線漸近線判別［17］等方法。無論是子構型拆分中的遞歸迭代，還是雙曲線漸近線交點的三線性插值計算，都使得計算的時間復雜度增加了一個量級。

圖6 等值面與體素相交方式的二義性

為加快體素等值面的判定，并消除二義性，本算法借鑒雙曲線漸近線判別法的思路［18］，并提出一點改進。通常情況下，等值面與體素相交形成的交線是一對雙曲線，該雙曲線與體素面上的位置關系如圖7所示。

圖7 雙曲線與體素面上的位置關系

可見，圖7（a）中雙曲線的兩支同時與體素的面相交，雙曲線將體素的面分割成3個區域。分別將兩組對邊上的交點用虛線連接，這兩條虛線形成的交點一定和其中一條對角線上的兩個頂點同處一個區域，即同為狀態“T”或“F”。通過比較該交點處的基本反射率值與閾值的大小關系，即可判定該二義性面與等值面的連接方式。

用圖8舉例說明，P1～P4是等值面與體素中一個面相交形成的4個交點，這4個交點的坐標可用2.2節所述方法計算得到，再通過聯立P1、P2和P3、P4的直線方程，可計算出兩條直線相交處O的坐標。由于A～D4個頂點的基本反射率值是已知的，因此可通過雙線性插值，計算出O點的基本反射率值，計算方法為：

圖8 二義性面的唯一性判定

式中：λA、θA和φA分別表示頂點A極坐標下的3個變量；Z（A）頂點A處的基本反射率值；Z（O）即為兩條直接相交處O點的基本反射率值。同樣用狀態“T”和“F”來表示該值與等值面閾值的大小關系。當Z（O）的狀態為“F”時，可確定圖8（a）的構型，當當Z（O）的狀態為“T”時，可確定圖8（b）的構型。

3 實驗結果及分析

3.1 實驗結果

為實現雷達三維回波的可視化，需將上述過程計算得到的一系列等值面用特定格式的文件輸出。目前主流的格式有：COLLADA是一種基于XML的3D交互文件格式，它通過對場景、節點、幾何形狀、著色器、力學和運動過程的描述，實現對三維矢量圖形的渲染和交互。圖形語言傳輸格式（Graphics Language Transmission Format，GLTF）是另一種常用的圖形語言交換格式，它用比XML更簡潔的JSON格式存儲信息，對OpenGL更友好，支持大數據量的3D Web實時渲染。

本實驗選用GLTF格式，將一組閾值的等值面依次輸出，通過Blender軟件加載20 dBZ等值面渲染后的效果如圖9所示。

圖9 采用Blender渲染的雷達三維回波（20 dBZ）

在天氣分析等教學實踐過程中，往往需要結合地理信息對雷達回波的特征加以分析，目前諸如Three.js、Cesium和PlayCanvas等開源軟件都對GLTF格式數據有很好的支持［19］。其中，Cesium是一個基于JavaScript可創建三維場景和虛擬地球的地圖可視化框架，在基于Web的地圖動態數據可視化方面具有優異的性能。

本實驗將上述閾值的等值面依次加載到Cesium，并用氣象上常用的色標對不同閾值的等值面渲染相應顏色，疊加地球影像和地圖圖像的顯示的效果如圖10所示。圖10（a）、（b）加載的是一同GLTF文件，不同之處在于觀測的視角和加載的地圖信息。

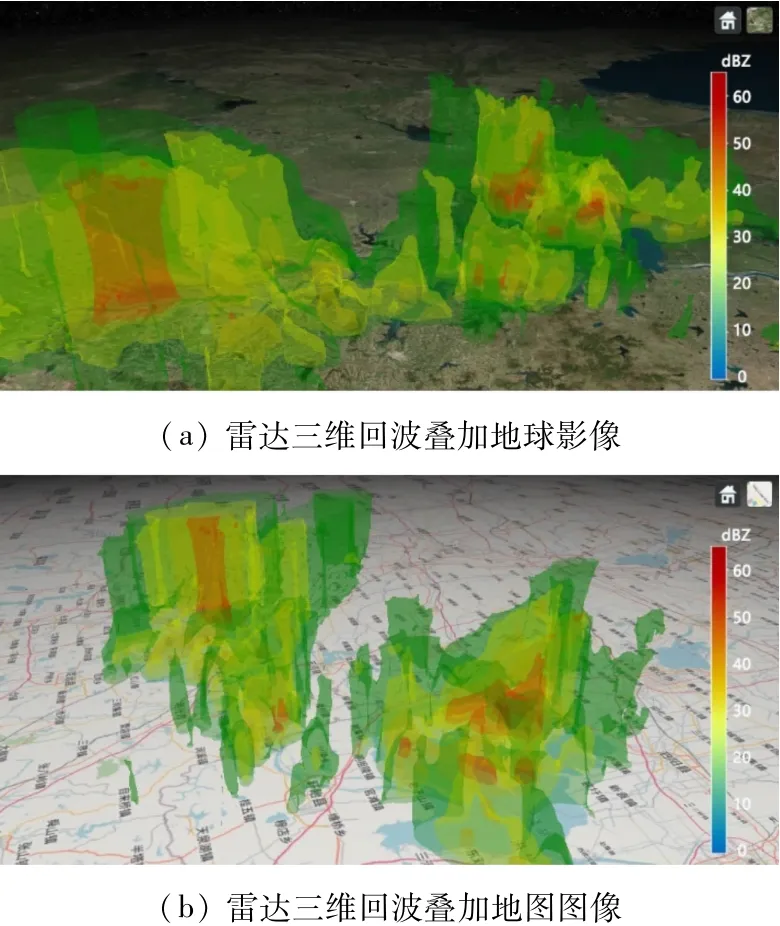
圖10 采用Cesium渲染的雷達三維回波

3.2 結果分析

改進傳統MC算法的計算效能，提升雷達三維回波渲染和交互的實時性是本算法改進的主要目標。為得到客觀量化的評價指標，以下測試采用相同的軟硬件環境。主要硬件配置為：Intel Xeon E5-1630 v4CPU，默認主頻3.7 GHz，DDR3 2400 MHz 128 GB內存。算法性能的評價主要包括兩個方面：一是計算耗時，它是評估等值面提取效率的重要指標，直接關系到是否滿足雷達數據實時渲染的性能要求；二是所生成的三角面片的總數量，雖然更多的三角面片使得圖形更加平滑，能有效減少鋸齒，但對內存的開銷很大。

表1中，“改進1”是以傳統MC算法為基礎，采用2.1、2.2節所述方法，不做空間插值和坐標轉換；“改進2”是在“改進1”的基礎上，增加2.3節所述方法進行相鄰體素狀態的快速判別。針對傳統MC的等值面二義性問題，上述測試均采用了2.4節所述方法進行處理。測試過程選用了不同時刻的雷達基數據，分別記錄不同算法下的計算耗時和三角面片數量，表1中的數值是10次測試的算法平均值取整。可見，傳統MC完成一次渲染需要27 s，其中大量時間消耗在坐標轉換過程的插值計算。以及等值面提取時對大量無價值體素的分析。“改進1”優化了上述缺陷，既降低了計算耗時，也減少了三角面片的數量，通過Edge瀏覽器加載Cesium和GLTF數據，監測內存發現，Edge進程占用內存減少了56%。“改進2”進一步降低了體素遍歷的數量，將計算耗時再度提升34%。

表1 改進算法性能對比

在實際操作過程中，采用“改進2”的計算方法，每次加載新的雷達基數據仍需近7 s的等待響應時間，如果將這些雷達基數據提前預處理好，生成GLTF文件存儲于服務器中，那么網絡加載GLTF文件并通過瀏覽器渲染的耗時將大幅降低到500 ms以內，達到實時交互、快速響應的目標。通過網頁異步傳輸、預加載等技術，可實現時序三維回波動畫的平滑播放，極大增強師生在天氣分析教學活動中的體驗。

4 結 語

利用曲面重建技術實現天氣雷達三維回波的實時渲染，為雷達氣象學、基于雷達資料的短臨天氣分析等教學實踐活動提供了更加直觀、立體、可交互的應用軟件平臺。本文設計的算法，針對雷達基數據的空間結構特點，著重在三角面片頂點位置的計算、三角剖分構型唯一性的判定以及包含等值面體素的加速遍歷3方面提出修改和優化，測試結果表明，改進后的算法計算耗時縮短至25%，內存占用降低了56%，滿足師生教學過程中，雷達數據渲染與交互的實時性要求。該算法也可應用于數值天氣模式、氣象衛星等資料的三維渲染，具有一定的推廣應用價值。