基于系統可靠度理論的抗滑樁加固邊坡穩定性研究

陳素玲，邢紅杰，宋葉房，趙軍紅

(1.河南省地礦局 第三地質勘查院，河南 洛陽 471023； 2.中鐵七局集團 鄭州工程有限公司，河南 鄭州 450000)

抗滑樁加固措施已經成為一種常用的邊坡加固技術[1-2]。目前在邊坡穩定性分析原理的應用上，無論是極限平衡法還是強度折減法，均利用安全系數來評估加固邊坡的穩定性[3-4]。安全系數法具有概念明確和使用方便的優勢，被眾多工程技術人員使用[2，5]。在邊坡實際工程設計中，受土體的變異性和測量誤差等因素影響，土體參數難以完全準確確定，導致邊坡穩定性分析中土體參數存在諸多不確定性[6]，從而導致邊坡的安全系數也存在不確定性[7]。在這種情況下，采用單一的安全系數不能真實準確地反映邊坡的穩定狀態，由于可以定量考慮不確定性參數對邊坡穩定性評價的影響，基于概率理論的可靠度分析方法在邊坡穩定性評價中受到了重視[6，8-9]。當邊坡土體參數不確定時，其最危險滑動面位置也不確定。因此，邊坡可靠度分析中需考慮多個滑動面的存在，采用系統可靠度方法對其進行相關分析[10]。

最近研究表明，當邊坡存在多個滑動面時，其可靠度常由相關性較小的少數代表性滑動面控制，邊坡的系統可靠度可通過代表性滑動面進行求解[10-11]。現有邊坡可靠度研究主要集中在無加固體的邊坡穩定性分析上，抗滑樁加固邊坡可靠度方面的研究還少見報道。其中，文獻[12]基于給定滑動面進行了抗滑樁加固的可靠度分析，沒有考慮多滑動面對邊坡可靠度的影響。文獻[13]基于土體從抗滑樁間產生的塑性流動、假定抗滑樁不失效情況下對抗滑樁加固邊坡進行系統可靠度分析。在實際抗滑樁加固工程中，因土體從抗滑樁間產生塑性流動失效的現象較為少見，而抗滑樁因抗滑力不足導致邊坡破壞是工程中更為關心的問題。目前，分析抗滑樁抗滑力大小對邊坡系統可靠度影響方面的研究還非常少見。

本文的目的是提出基于可靠度理論的邊坡抗滑力系統分析方法。首先介紹抗滑樁加固邊坡的系統可靠度模型以及模型的求解方法，通過算例來研究不同因素對抗滑樁加固邊坡系統可靠度的影響。

1 抗滑樁加固邊坡系統可靠度模型

1.1 安全系數計算方法

抗滑樁加固邊坡如圖1所示。

圖1 抗滑樁加固邊坡的示意Fig.1 Schematic of slope reinforcement with anti slide piles

所采用的抗滑樁直徑為D，抗滑樁中心距設為D1。當土體強度參數存在不確定性時，邊坡的最危險滑動面位置也不確定。對于某一半徑為R的圓弧滑動面，抗滑樁與滑動面相交處以上的埋置深度為h，相交處滑動面與水平方向夾角為α。為簡單起見，可將抗滑樁的加固作用簡化為與滑動面相交處的一個水平力V。文獻[14]所列的簡化畢肖普法作為計算邊坡安全系數的常用方法，滑動面的安全系數Fs可根據式(1)計算：

(1)

式中，MV為由樁加固作用提供的力矩，如式(2)：

(2)

1.2 可靠度模型

假定抗滑樁距很小，土體不會從樁間產生塑性滑動破壞。此時，邊坡將因抗滑力不足而產生失穩。假設邊坡存在n條可能的滑動面。設x為土體不確定性參數，gi(x)為第i個滑動面上安全系數與變量x之間的關系。由于邊坡沿任一滑動面滑動都會導致失穩，邊坡的失效域可用式(3)來表征：

(3)

式中，mingi(x)為給定參數x條件下n條滑動面的最小安全系數，i=1，2，…，n。

令f(x)為不確定變量x的概率密度函數，根據可靠度理論，邊坡的系統失效概率Pt按式(4)計算：

(4)

2 可靠度模型求解方法

2.1 基于代表滑動面的可靠度分析

為考慮n個滑動面對系統可靠度的影響，式(4)可采用蒙特卡羅抽樣等方法求解。近年來的研究表明，雖然邊坡存在大量的潛在滑動面，但只有少數滑動面對邊坡系統可靠度起控制作用，這些滑動面通常被稱為代表性滑動面。本文將采用代表性滑動面對邊坡系統可靠度進行求解。在該方法可按下面步驟進行實施：①采用一階可靠度方法計算單個滑動面的可靠度指標；②搜索代表性滑動面；③基于代表性滑動面的可靠度指標計算其失效概率。

2.2 一階可靠度方法

令βi(V)代表抗滑力為V條件下、第i個滑動面的可靠度指標。根據一階可靠度分析原理[15]，βi(V)按式(5)計算：

(5)

式中，y為x轉換到標準正態空間中的變量；R為隨機變量的相關矩陣。

本文采用簡化畢肖普方法求解邊坡安全系數，功能函數為隱式。對于給定的滑動面，其安全系數與輸入參數之間的關系往往具有很好的線性關系[16]。為方便式(6)中可靠度的求解，可用如下二次多項式來模擬第i個滑動面安全系數與輸入參數之間的關系：

(6)

式中，r為隨機變量的數量；aj(j= 0，1，…，2n)為待定系數，其中總共有2n+1個待定系數，對應需要2n+1個取樣點來確定這些待定系數的值。

將取樣點代入到數值分析軟件中，獲取對應的安全系數，從而逆向求取待定系數的值。

2.3 代表性滑動面的確定

對于同一個邊坡，位置相近的滑動面間的安全系數是高度相關的。因此，盡管一個邊坡可能有無數個滑動面，系統失效概率實際上由少數的代表性滑動面決定[17]。不同滑動面安全系數的相關性可通過相關系數來衡量：

(7)

式中，ρAB為滑動面A和滑動面B間的相關系數；yA、yB分別為其標準正態空間中設計點構成的向量；βA、βB分別為滑動面A和滑動面B的可靠度指標。令ρ0表示判別滑動面安全系數的相關性閾值。獲取不同滑動面安全系數的相關系數后，代表性滑動面可按下述流程來識別[10]，如圖2所示。

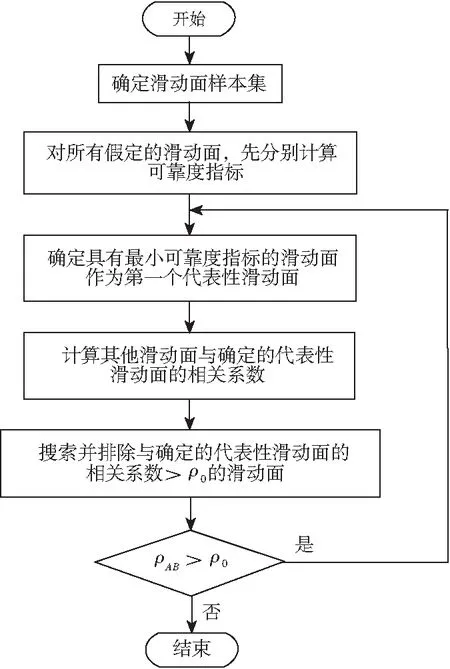
圖2 選取代表滑動面流程Fig.2 Select representative sliding surface process

2.4 系統失效概率計算

獲取所有代表性滑動面后，結合文獻[18]提出的窄界算法、文獻[19]提出的聯合失效域算法等，綜合使用多種方法計算系統失效概率。本文采用文獻[20]提出多失效模式系統可靠度方法進行系統失效概率計算：

pf(V)=1-φn{-β1(V)，-β2(V)，…，

-βn(V)；λ}

(8)

式中，βi為第i個代表性滑動面的可靠度指標；φn為n重聯合正態分布累積函數；λ為不同設計點間的相關系數矩陣。

3 算例分析

結合圖3示例的雙層土模型來論證本文所述方法，設定2層土的土體重度為19 kN/m3。假定c1和φ1為上層土體的黏聚力和內摩擦角，令c2和φ2為下層土體的黏聚力和內摩擦角。假定示例中的不確定性強度參數均服從對數正態分布且統計獨立。在響應面擬合過程中，設置仿真步長為2.03。示例的邊坡強度參數見表1。

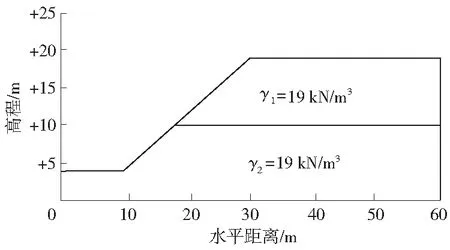
圖3 邊坡幾何示意Fig.3 Schematic of slope geometry

表1 邊坡的強度參數Tab.1 Strength parameters of slope

未加固求解的代表性滑動面[21]如圖4所示。由圖4可知，當邊坡不采取加固措施時，其系統可靠度由2個代表性滑動面控制，其可靠度指標分別為0.297、2.319。此時，邊坡的系統可靠度指標βs和失效概率Pt分別為0.282和38.9%，失效概率較大。為論證抗滑樁的加固效果，假定所布抗滑樁的直徑D取1 m，間距D1取1 m、抗滑樁距坡角距設置s=12 m，每根抗滑樁提供的水平抗滑力約1 000 kN。采用本文方法分析后，此時邊坡具有2條代表性滑動面，如圖5所示。由圖5可知，由于受到抗滑力的干預，2條代表性滑動面的位置和未加固時代表性滑動面的位置有顯著區別。此外，加固后2條代表性滑動面的可靠度指標分別為2.360 和3.304，對應的可靠度指標βs和系統失效概率Pt分別為2.340和1.0%，降低了失效概率。

圖4 未加固求解的代表性滑動面Fig.4 Representative sliding surface for unreinforced solution

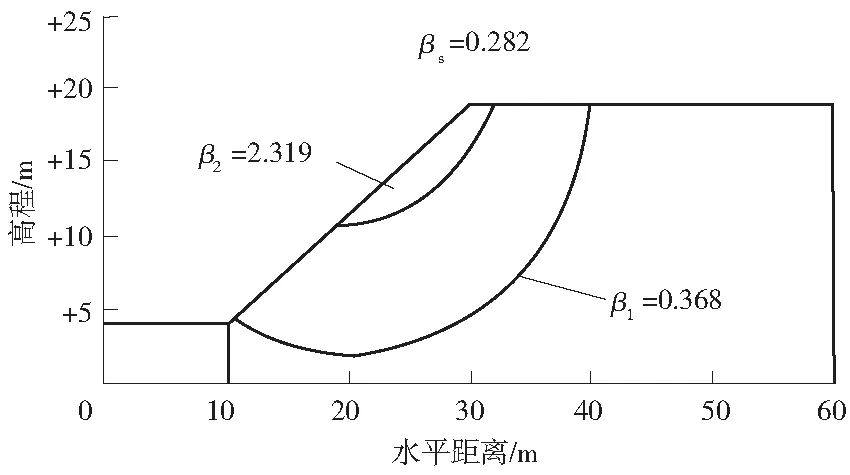
圖5 加固求解的代表性滑動面Fig.5 Representative sliding surface for reinforcement solution

3.1 樁位置對系統可靠度的影響

為詳細探討抗滑樁的位置對系統可靠度的影響，圖6給出樁徑D=1 m、樁間距D1=1 m，水平力V=1 000 kN條件下，抗滑樁加固位置和坡腳的距離s分別為4、8、12、16、20、24 m時代表性滑動面和其可靠度指標。

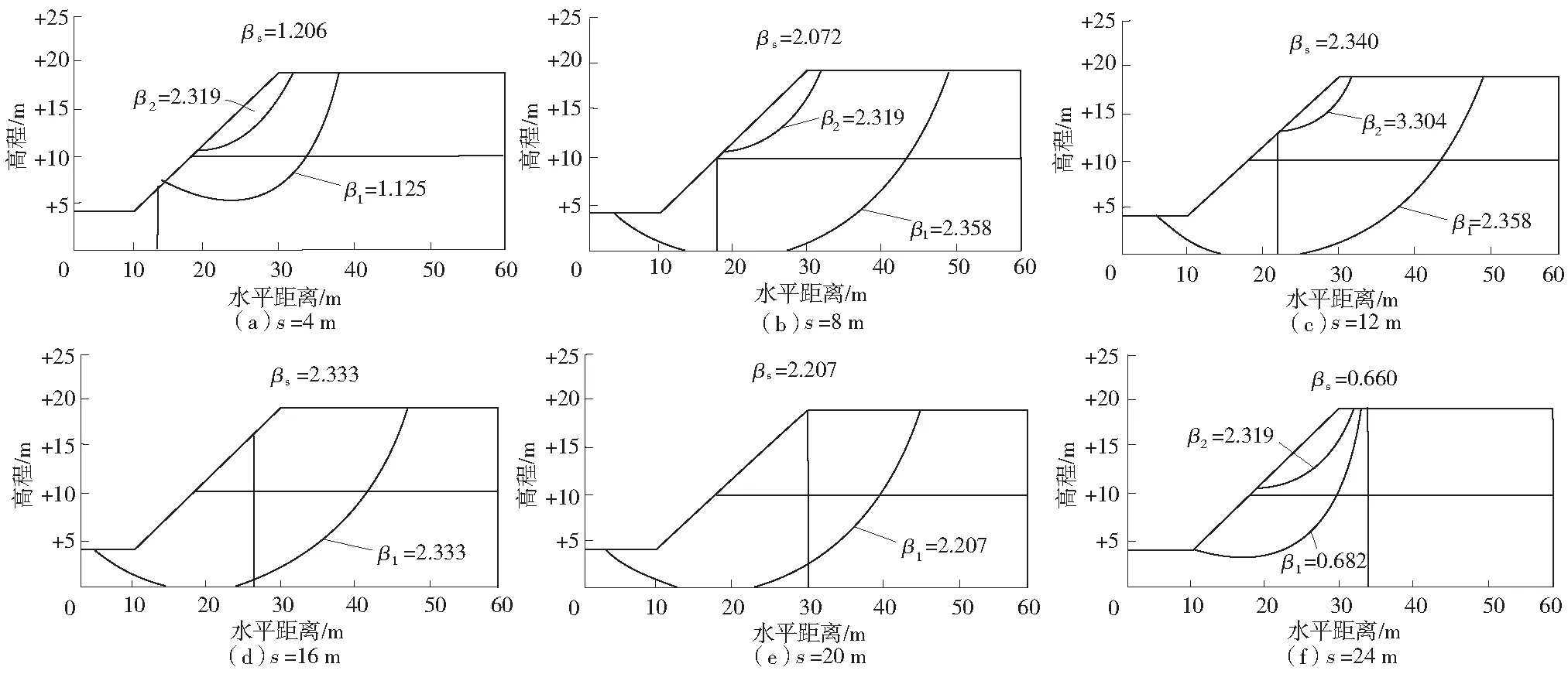
圖6 抗滑樁位置對系統可靠度的影響Fig.6 Influence of anti slide pile position on system reliability

由圖6可知，當s取4、8 m 時，僅穿越上層土體的代表性滑動面2保持不變，而代表滑動面1的可靠度指標β1增大，系統可靠度指標βs相應增加；當s取12 m時，抗滑樁開始同時影響2個代表性滑動面，系統的可靠度指標取βs=2.340；當s設置16 m和20 m時，僅存在1個代表性滑動面，而系統的可靠度指標βs呈現下降趨勢，分別2.333和2.207；當s取24 m時，抗滑樁位于坡頂，其代表性滑動面位于抗滑樁加固范圍外，系統的可靠度指標βs降為0.660。圖7顯示了直徑D=1 m、間距D1=1 m、水平力V=1 000 kN條件下的邊坡可靠度指標和抗滑樁位置s間的關系。由圖6可知，當抗滑樁位于距坡腳s=12 m時，邊坡的可靠度指標達到最優。此外，圖7還反映了邊坡的系統可靠度取決于最小的可靠度指標的代表性滑動面，即說明邊坡的可靠度具有明顯的系統效應。則采用最危險的滑動面的可靠度指標來衡量邊坡的可靠度偏于危險。

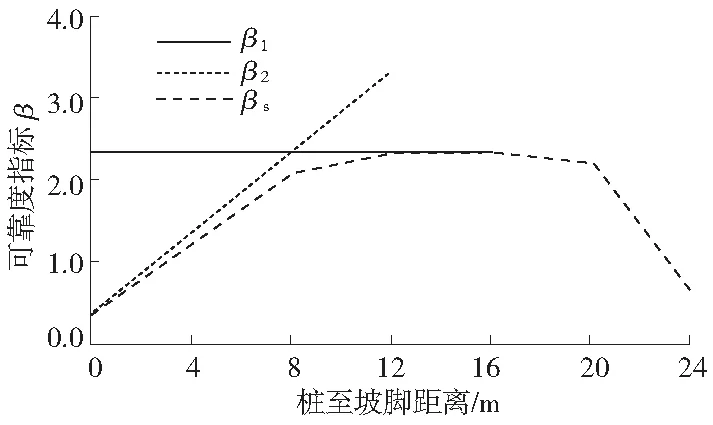
圖7 不同代表性滑動面可靠度指標 和系統可靠度指標對比Fig.7 Comparison of different representative sliding surface reliability indexes and system reliability indexes

3.2 抗滑力對系統可靠度的影響

為了進一步分析抗滑力對邊坡的穩定性影響，樁徑D=1 m、樁間距D1=1 m條件下邊坡系統的可靠度指標同抗滑力和抗滑樁位置的關系如圖8所示。在給定抗滑力條件下，邊坡系統的可靠度指標隨抗滑樁位置變化呈先增大后減小趨勢，即存在一個最佳加固位置。文獻[20]論證了路基邊坡的目標可靠度指標為2.3。為減小樁長，在荷載為1 000 kN時，圖8中s=12 m作為最佳設計方案。

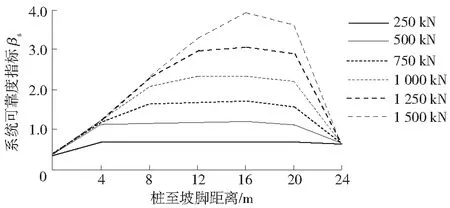
圖8 不同加固荷載條件下邊坡系統 可靠度指標隨樁位置變化Fig.8 Reliability index of slope system varies with pile position under different reinforcement load conditions

4 結語

鑒于抗滑樁加固邊坡的工程問題，本文提出了一種基于可靠度理論的邊坡抗滑力分析模型，結合代表性滑動面分析原理建立了相應求解方法。算例分析表明，抗滑樁對邊坡的代表性滑動面位置和可靠度指標具有重要的影響；在同等的抗滑力下，抗滑樁加固邊坡存在一個最優的加固位置。所提方法適用于基于可靠度理論確定抗滑樁的加固位置和抗滑力，有助于抗滑樁加固邊坡的工程設計。