污染源變化條件下地下水監測網優化設計

黃瑞瑞，王錦國，楊 蘊

(河海大學 地球科學與工程學院，江蘇 南京 211100)

近年來，地下水環境不斷惡化，地下水污染問題日益突出。在地下水污染防治和修復過程中，建立和完善地下水污染監測網是獲取準確的地下水污染信息的必要先決條件[1-2]，是實現可持續發展和保證人類身心健康的重要工作，利用地下水污染監測可以實時掌握地下水水質變化規律，以便及時有效地監測和預警該地區地下水污染情況。由于地下水污染源往往呈現多點分布，污染源的變化影響著監測井的空間布局和數量選擇。因此，在場地地下水污染監測網設計時，還需考慮多個污染源對監測網絡設計的影響。

關于地下水污染監測網的設計，我國自20世紀50年代建立監測井網以來，已經形成了一定規模的監測網絡，具有較為完善的管理和監測體系[3]。但是，在地下水水質監測的過程中，過量取樣是較為普遍的現象[4]，它將導致監測數據冗余，而且地下水監測又是長期的工程，這便意味著巨大的經濟成本浪費。因此，在保證監測精度的前提下，如何尋求優化的地下水污染監測方案使得監測成本最低，是地下水監測網優化設計的關鍵技術難題。

20世紀70年代末，國外學者開始著手進行地下水監測網的優化設計，提出了很多經典的方法來解決昂貴的監測費用問題，比較典型的方法有Kriging法、水文地質分析法、聚類分析法、卡爾曼濾波法、信息熵法等[5]，但這些方法均未綜合考慮水文地質信息、監測井位、監測井數、計算量和人為主觀因素對地下水監測網優化設計的影響[6-7]。本文運用模擬—優化方法對理想場地污染源變化條件下的地下水監測網進行優化設計，在不顯著影響采樣數據的準確性和充分性的情況下，通過剔除多余的監測井來實現長期監測成本最低的目標，并對不同的優化結果進行對比分析。

1 地下水污染監測網設計模擬—優化技術

本文采用的模擬—優化方法，包括3個主要組成部分，即地下水流和溶質運移模擬、地下水污染監測網優化設計模型以及基于遺傳算法(GA)的最優搜索技術[8]。前兩者是用于評估所有潛在采樣設計的各種約束條件，而第3個部分是用于識別最優或接近最優的地下水污染監測網采樣設計。研究中用于實現具有成本效益的地下水監測網采樣優化設計的步驟如圖1所示。

1.1 地下水流和溶質運移模擬

本文假定的地下水流和溶質運移模型是基于三維有限差分流動程序MODFLOW和溶質運移程序MT3DMS，2個程序共同來模擬地下水污染物在不同時間段的空間分布和變化情況，從而獲取在不同位置上的污染物真實濃度值[9]。MODFLOW具有模塊化結構，使其易于適應特定的應用程序；MT3DMS也同樣具有模塊化結構，并具有模擬污染物運移的功能，可評估污染物運移情況。

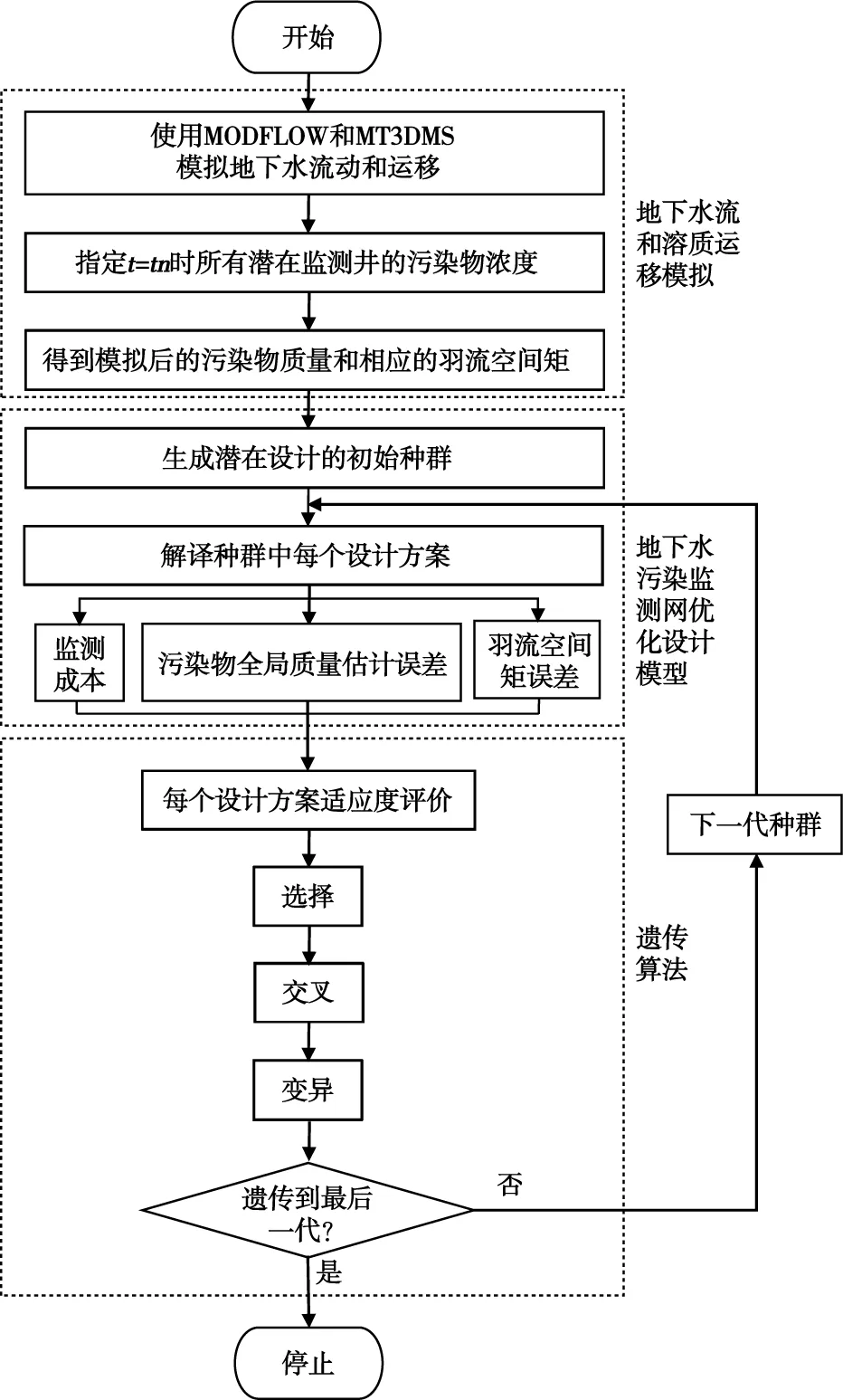
圖1 基于GA的地下水采樣網絡設計模擬—優化流程Fig.1 Flow chart of GA-based groundwater sampling network design simulation-optimization method

1.2 地下水污染監測網優化設計模型

污染物在地下水含水層中某一特定時刻的空間分布情況可以用污染物總質量(零階矩)、污染羽流質心的位置(一階矩)、污染羽流圍繞質心的空間分布范圍(二階矩)來描述[10]。當這3個物理特征值都已知時，就可以刻畫出污染羽流的空間分布狀態。

地下水污染羽流中污染物總質量可由式(1)表示：

(1)

羽流質心在t時刻的坐標位置由關于原點的一階矩定義，可以表示為[11]：

(2)

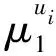
污染羽流的二階矩描述了羽流圍繞質心擴散的度量，用空間協方差張量表示：

(3)

(4)

空間協方差張量的分量項與羽流濃度分布在其質心周圍的分布情況相關，在應用中，必須從一組離散的指定點濃度中估算矩的大小。在這項研究中，上述內插濃度可用于估算整體質量以及第一和第二階矩，以便與從流動和運移模型直接輸出的污染物羽流分布作比較。插值的方法是普通克里金(OK)或逆距離加權(IDW)插值方法。

如果在各種潛在設計中監測井選擇足夠多，即取樣點選擇越多，那么插值后得到的地下水污染羽流與模擬所得到的羽流相比差別會越小或趨于一致，但如此一來，監測成本就會上升。因此，在監測成本和污染羽流精度之間存在著一種權衡關系。本研究中監測問題的目標函數是最小化長期監測成本，同時保持污染物質量和羽流矩估計的準確性。目標函數是所有采樣點的總安裝/鉆井和采樣成本的總和，那么監測問題可以表示為：

(5)

errormass≤εmass

(6)

errormoment≤εmoment

(7)

式中，J為井安裝/鉆井和采樣總成本的管理目標；n為潛在監測井總數；C1為每次采樣的成本；xi為二進制變量，表示第i井是否采樣(如果是，則xi=1；如果否，則xi=0)；li為第i井在不同深度處的采樣數；C2為第i井每單位深度安裝/鉆井的固定成本；yi為二進制變量，表示位置i處是否需要鉆井(如果是，則yi=1；如果否，則yi=0)；di為第i井的深度。

式(6)、式(7)分別為對總體質量估計誤差和羽流矩估計誤差的約束。總溶解污染物質量估計誤差errormass可以表示為：

(8)

式中，masscal為由流動運移模型確定的模型域內污染物總質量；massj為采用第j個取樣設計通過插值后得到的污染物總質量。

由于空間矩張量包含不同的分量，羽流矩估計誤差errormoment可以表示為：

(9)

1.3 遺傳算法

遺傳算法(GA)是由Holland[12]在1975年開發的一種使用自然選擇機制在決策空間搜索最優解的技術，它能夠模擬自然選擇的生物進化過程和達爾文生物進化理論的遺傳機制[13]。

對于任何一個地下水污染監測網設計問題，都有n個潛在的監測井位置。遺傳算法認為每個采樣方案是由n個0或1組成的字符串，其中第i位的值為1表示從第i個位置采樣，0表示不采樣。字符串中非零數字的和表示當前設計中使用的采樣位置的數目。

遺傳算法由選擇、交叉和變異3個遺傳算子組成[14-15]。首先在每一代種群中評估所有字符串的適應度大小，其次根據適應度大小選擇多個字符串，最后使用交叉和變異遺傳算子進行繁殖、突變以形成新種群[16]，母種群被后代種群取代。隨著世代的發展，獲得最優或接近最優的采樣設計。

1.3.1 選擇過程

遺傳算法的第一個階段是選擇單個字符串(采樣備選方案)，具有高適應度的字符串將有更高的概率被篩選出來進入交配池以繁殖后代。對于等式(5)—(7)中提出的監測網設計問題，目標是在考慮總體質量估計和矩估計精度的同時，最小化采樣成本。因此，適應度函數必須考慮到約束條件，可以通過在目標函數中添加任何違反約束的量作為懲罰來定義適應度函數：

F=J+V1+V2

(10)

(11)

(12)

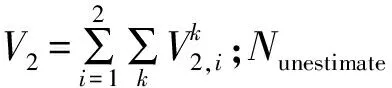
1.3.2 交叉過程

遺傳算法的第2個階段是交叉，交叉操作以一定的概率Pcross從交配池中選擇2個字符串(父、母親)創建2個新的字符串(子代)。因為采樣網絡設計的任務是決定是否選擇一個潛在的采樣地點(即1或0)，所以均勻交叉最適合本研究。通過均勻交叉，在一個字符串的特定位置上的選定位與在另一個字符串相同位置上的相應位交換。交叉之后，新一代的字符串數量與上一代相同。

1.3.3 變異過程

遺傳算法的第3個階段是變異，對于經歷了交叉后的子代字符串，變異會在字符串上逐位進行，是否變異取決于變異的概率Pmute。某一字符串的變異操作就是根據變異概率對某一個字符取反，即將0變為1，1變成0。變異概率一般很小，因為變異針對的是某一字符而非字符串[17]。該操作的主要目的是保持字符串的多樣性，也是為了更好地優化全局地下水污染監測網設計[18]。

選擇算子旨在保留那些具有較高適應度的采樣設計，交叉算子是通過結合較高適應度的采樣計劃來提高采樣效率，而變異過程旨在防止信息不可挽回的丟失[19]。

2 單、雙污染源地下水監測網優化設計案例

2.1 場地概況及地下水流和溶質運移模擬結果

本算例涉及到的是二維均質各向同性的承壓含水層。假設一個含水層系統平面圖及模型的平面中心有限差分網格，研究區域x方向延伸長600 m，y方向延伸長400 m，含水層左側為恒定水頭邊界，上水頭為89.0 m，下水頭為89.5 m，自上而下線性漸升；右側為恒定補給邊界；頂部和底部是隔水邊界，其他含水層相關參數如下：孔隙度為0.175；含水層厚度為10.0 m；縱向彌散度為6.0 m；橫向彌散度與縱向彌散度之比為0.1；恒定補給量為9.45 m3/d；縱向格距為20.0 m；橫向格距為20.0 m；滲透系數為8.9 m/d。

假設在圖中污染源處發生了泄漏，污染源初始污染物濃度為1×10-6，污染羽流隨水流向左邊界移動。本研究考慮的是自污染物泄漏以來前3年作為監測期，基于56個監測位置的插值羽流污染物總質量、一階矩、二階矩與使用研究區內所有節點污染濃度值的流動運移模型的輸出結果相當接近。單、雙污染源場地第一個監測周期結束時由流動和運移模型計算出的污染羽流“真實”分布狀態如圖2、圖3所示。

圖2 單污染源含水層結構平面圖及模型網格示意Fig.2 Schematic diagram of the structure plan and model grid of the single pollution source aquifer

2.2 目標函數及優化參數設置

此算例的監測網優化設計模型可利用式(5)—(7)表示。假設采樣的成本(C1li)和固定安裝/鉆井的成本(C2di)為每口監測井2 000美元。違反污染物總體質量和污染羽流矩估計誤差的懲罰系數為每口監測井總成本的5倍(即α1=α3=10 000)，考慮到矩估計的相對誤差可能大于質量估計相對誤差，因此這里假設εmoment>εmass。

其他參數設置如下：遺傳代數100代；種群大小600；交叉概率Pcross=0.65；變異概率Pmute=0.01；每口監測井的安裝與采樣成本2000美元；潛在監測井數目56口；允許的空間矩誤差Emoment=0.10；一、二階矩權重W=1.00；超出允許監測井數量的懲罰系數α0=1×1010；質量估計誤差的懲罰系數α1=1×104；未估計點濃度懲罰系數α2=50；羽流矩估計誤差懲罰系數α3=1×104。

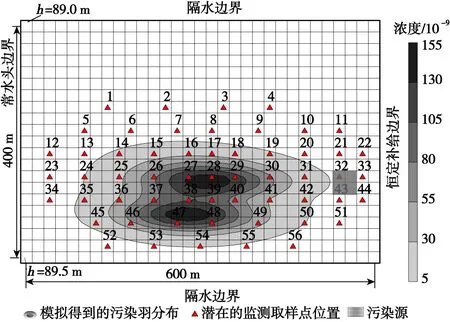
圖3 雙污染源含水層結構平面圖及模型網格示意Fig.3 Schematic diagram of the structure plan and model grid of the dual pollution source aquifer

3 監測網優化結果及對比分析

3.1 優化結果

經過100代后，以最小目標函數進行了最優采樣設計。對于單污染源地下水監測網優化設計，在權衡監測精度的前提下，采用OK和IDW插值方法對模型域內未采樣點進行濃度插值，結果顯示取樣井數分別為37口和28口，能分別節省33.93%和50%的監測成本，優化后的取樣井位和羽流分布情況如圖4所示。

對于雙污染源場地，在權衡監測精度的前提下，采用OK和IDW插值方法進行地下水監測網優化設計時，取樣井數均為25口，可節省55.36%的監測成本，優化后的取樣井位和羽流分布情況如圖5所示。

3.2 確定污染源條件下不同插值方法的對比

以上算例的最優采樣設計是將遺傳代數設為100代的優化結果，為方便比較確定污染源條件下不同插值方法對最優采樣設計的影響，現將遺傳100、200代的試驗結果列出，見表1。

觀察表1中算例PM1、PM2可知，當污染源只有一個時，基于IDW插值方法的優化設計取樣井數更少，能節省更多的成本，更具有成本效益。由圖4可知，發現基于OK插值后的羽流與流動運移模型輸出的羽流接近一致，明顯優于IDW插值后的羽流分布。因為根據表中顯示的質量估計誤差和矩估計誤差來看，基于OK的方法得到了更準確的污染物質量和羽流一、二階矩估計，尤其是二階矩估計。綜上，對于單污染源場地，基于2種插值方法的采樣設計各具優缺點，但在實際應用中，更多地使用OK插值方法，因為采樣設計的成本效益不應以犧牲污染物全局質量和矩估計的精度為代價。在大規模的現場應用中，IDW不適合作為最優采樣設計的插值方法。

圖4 地下水污染監測網基于OK、IDW的最佳 采樣設計(單污染源)Fig.4 The best sampling design of the groundwater pollution monitoring network based on OK and IDW(single pollution source)

觀察表1中算例PM3、PM4可知，當污染源有2個時，基于2種插值方法的優化設計取樣井數相差不明顯或出現與單污染源設計相反的結論。由圖5可知，基于2種插值方法的優化設計羽流估計誤差相差很小，且無規律，隨著遺傳代數的增加，基于OK與IDW優化設計的精確度也隨之變化，有時基于OK插值方法的優化設計更精確更具成本效益，有時則相反。隨著遺傳代數的增加，基于IDW插值方法的優化設計結果精確度不斷提高。與單污染源算例相比，對雙污染源的場地進行地下水污染監測網優化設計能獲得更準確的羽流二階矩估計，且能節省更多的潛在費用。因此，對擁有2個污染源的場地進行地下水污染監測網優化時應用2種插值方法都可行，都可以在保證污染羽流估計準確度的同時，降低所需的監測成本。若對計算速度和精度要求較高時，可選擇IDW插值方法。

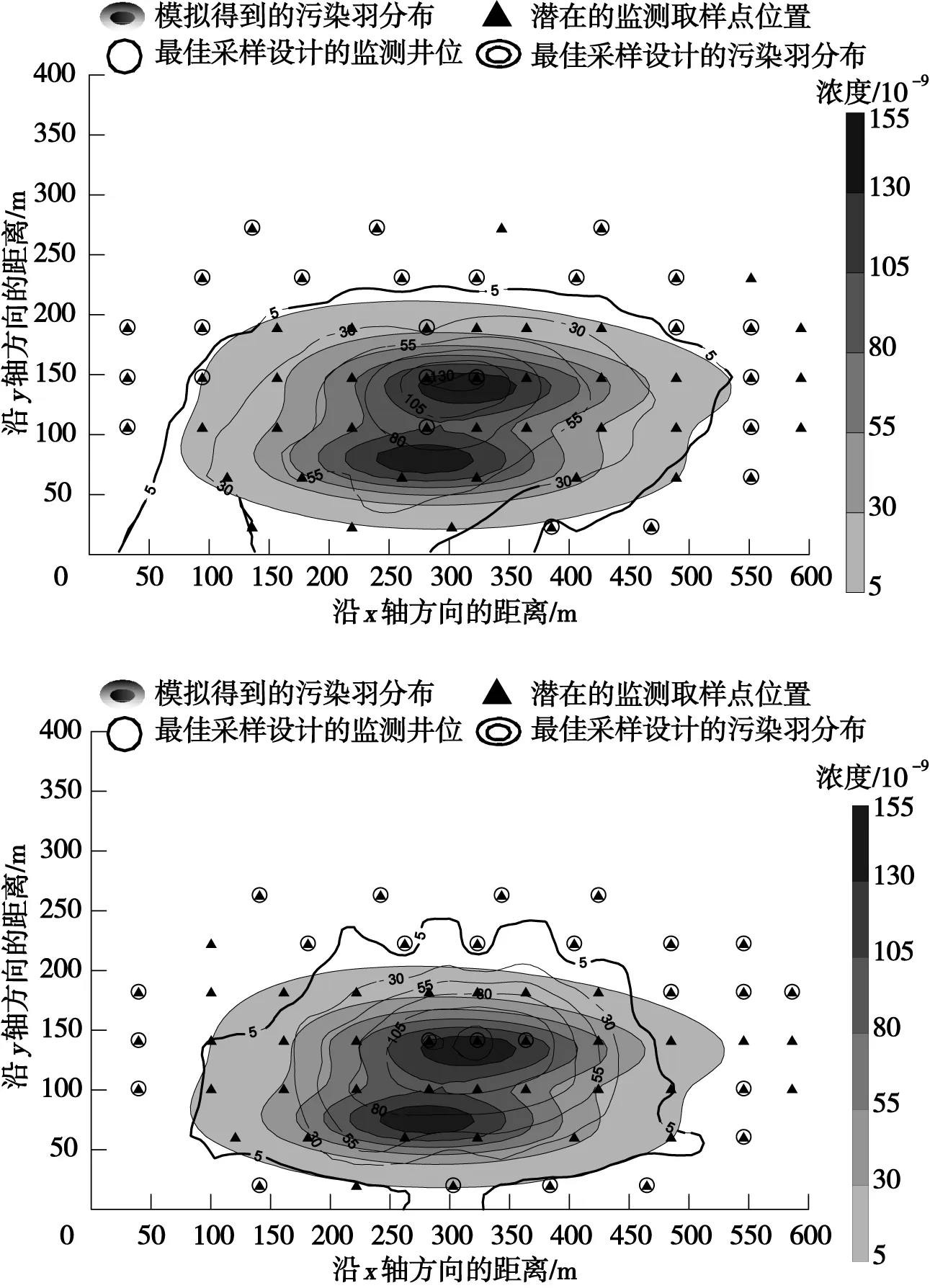
圖5 地下水污染監測網基于OK、IDW的最佳 采樣設計(雙污染源)Fig.5 The best sampling design of the groundwater pollution monitoring network based on OK and IDW (dual pollution sources)

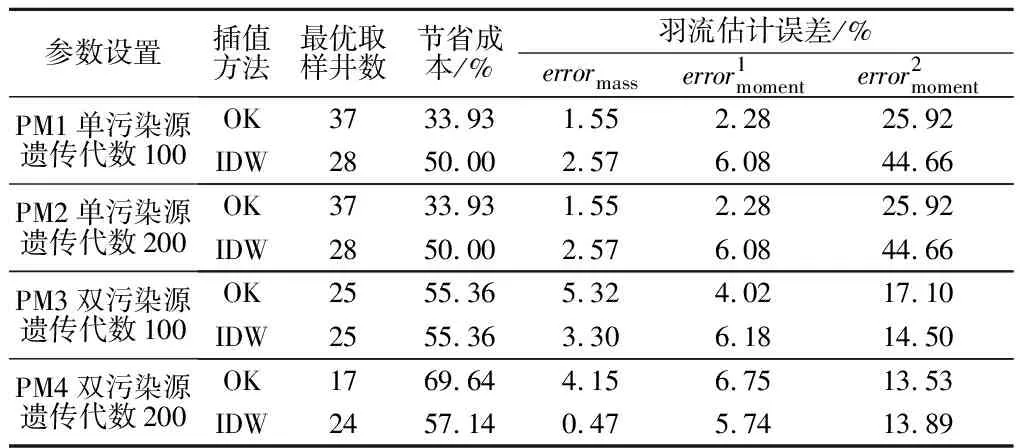
表1 單、雙污染源地下水監測網優化結果Tab.1 Optimized results of groundwater monitoring network for single and double pollution sources

3.3 單、雙污染源對優化結果收斂的影響

很難知道什么時候最優或接近最優解是使用遺傳算法的一個難點，Reed等[20]指出遺傳算法在收斂前必須滿足2個條件。①潛在采樣位置的一個子集必須由上一代中大約90%的個體選擇；②所有剩余的采樣點不能被上一代中超過10%的個體選擇。

研究采用的遺傳代數是根據大量試驗得出的，采用的是在目標函數(包含懲罰量)不發生顯著變化或不變化時的代數。目標函數隨遺傳代數的演化如圖6所示。在單污染源場地，遺傳算法中的目標函數會隨著遺傳代數的增加不斷減小，最后趨于穩定值，基于OK插值方法的優化設計目標函數在第64代時收斂，之后便不再發生變化，基于IDW插值方法的優化設計目標函數在第82代時收斂。在雙污染源場地，兩種插值方法的優化設計目標函數隨著遺傳代數的增加，起初減小的幅度很大，在大約50代之后，變化幅度很小，但不能收斂到一個值。

圖6 目標函數隨遺傳代數的演化Fig.6 The objective function evolves with genetic algebra

觀察圖6可知，無論是單污染源還是雙污染源情況下，將遺傳代數定為100代是比較合理的。由圖6可知，對單污染源的場地進行地下水污染監測網優化時盡量考慮OK插值方法；對雙污染源場地進行監測網優化時，2種插值方法均可使用，可以采用一種插值方法計算，另一種方法進行驗算。

4 結論

(1)將模擬—優化方法應用到本文算例中，在不顯著降低污染物總體質量和羽流矩估計精度的前提下，可以實現高達50%～60%的潛在成本節約。且在使用該方法時需要在目標函數中添加約束違反量，用于權衡減少監測成本與提高質量和羽流矩估計精度這2種相互矛盾的目標。

(2)對于本文的場地提出的監測網優化模型，當污染源只有1個時，基于IDW插值方法的優化設計與基于OK插值方法的優化設計相比，取樣井數更少，能節省更多潛在的成本。但是基于OK插值方法的優化設計能夠得到更準確的總體質量估計和羽流矩估計，因此，在實際應用中，更多采用的是基于OK插值方法的優化設計方案。

(3)當污染源為2個時，基于2種插值方法的優化設計取樣井數、污染物質量、一階矩、二階矩估計誤差相差不明顯，且變化無規律。隨著遺傳的進行，基于OK與IDW插值方法的優化設計的精確度也隨之變化，有時基于OK插值方法的優化設計更精確、更節省成本，有時則相反。在實際應用中，兩種插值方法都可采用。

(4)目標函數(含懲罰量)隨著遺傳代數的增加，逐漸趨于定值或變化很小。在單污染源場地，目標函數會隨遺傳的進行收斂到一個定值，將此定值所對應的最小遺傳代數作為終止遺傳算法的條件較為合理；在雙污染源場地，隨著遺傳的進行，目標函數變化幅度逐漸變小，但不收斂到某一值。

(5)與單污染源相比，在保證地下水污染羽流估計精度的前提下，對雙污染源的場地進行地下水污染監測網優化更具成本效益。