基于邊緣計算的電力系統穩態數據壓縮方法

劉玉林，田 浩，張 利，田文輝，劉喜軍，吳肇赟

(1.中國石化集團 勝利石油管理局有限公司電力分公司，山東 東營 257000； 2.電力系統及發電設備控制 和仿真國家重點實驗室(清華大學 電機系)，北京 100084； 3.南京信息工程大學 濱江學院，江蘇 無錫 214105)

國民經濟不斷上升，電網規模日益壯大，電力系統逐漸朝多樣化、復雜化方向發展。通過有效記錄下海量電力數據，才能滿足數據分析、故障監測、廣域測量[1]等電力管控需求。若儲存、傳輸電力系統工作時所生成的大規模數據，就會極大程度地增加運行速率與存儲空間負擔，甚至會阻礙電網跨越式地智能化發展。在近幾年的電力發展中，企業與用戶的要求標準越來越高，數據壓縮技術[2]受到了前所未有的高度關注，該項技術在一定程度上有助于減緩數據儲存與傳輸的壓力。

基于上述背景，文獻[3]針對船舶電力監控系統，利用旋轉門算法壓縮監控數據，采用小波變換法壓縮電能質量數據，通過十進制霍夫曼編碼壓縮開關量等數據；文獻[4]就智能配電網的異構數據，設計一種結構化數據與一種非結構化張量處理模型，根據張量Tucker分解方法，構建出數據壓縮方法，確保在壓縮階段使數據空間本征結構得以留存。

電力系統中的穩態數據作為狀態分析、故障診斷、故障預測等的參考依據，有助于保障電網平穩運行，本文面向此類數據提出一種基于邊緣計算的壓縮方法。邊緣計算技術在匯總數據與智能分析方面，可有效解決高通信成本、延時過長等問題；引入小波變換算法，能強化壓縮效果，增加壓縮比，并大幅減少存儲空間；通過字典更新，有助于提升初始信號稀疏程度與重構信號信噪比；采用高斯測量矩陣，可以減少測量數與運算量；利用正交匹配追蹤算法自適應調節迭代補償，能加快收斂速度，增強信號重構性能。

1 邊緣計算下電力系統穩態數據融合

基于分布式壓縮感知技術[5]，通過建立聯合稀疏模型、建立稀疏冗余字典、明確測量矩陣、建立聯合重構算法4個步驟，實現壓縮感知與分布式信源編碼融合。

(1)建立聯合稀疏模型。時域上的電力系統穩態數據沒有稀疏性，只有利用稀疏基稀疏分解穩態數據后，才能使用分布式壓縮感知技術進行采集、融合。因穩態數據的信號頻率含有次諧波與基波，故初始稀疏基用傅里葉正變換矩陣表示，建立聯合稀疏模型來采集穩態數據。信號不存在共同部分，可通過一個稀疏基完成新息部分(即系數向量與共同部分之差)的稀疏表示。假設初始穩態數據信號是xj，共同部分與新息部分分別為zc、zj，則信號xj的稀疏為：

xj=zc+zj=zj=ψθj

(1)

式中，ψ、θj分別為稀疏矩陣與相應稀疏系數。

(2)創建稀疏字典。稀疏程度與原子數量、上傳數據量間呈負相關。為確保原子與初始信號實現自適應匹配，引入字典訓練算法中的學習型稀疏字典[6]，經多次字典更新，減小初始信號與重構信號的偏差，使重構信號信噪比符合預設閾值。

(2)

其約束條件如下：

(3)

式中，y為重構的穩態數據信號；ε為預設閾值；N為原子數量；F為稀疏系數矩陣范數。

在字典更新時的循環計算中，字典訓練算法每次只對一個原子作出更新處理。當取得新原子時，下列等式成立：

(4)

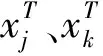
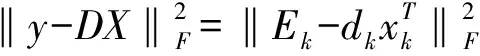
(5)

假設原子dk的重構信號索引為ωk，N×ωk的矩陣為Ωk，若除(ωk(i)，i)是非零值外的矩陣元素均為零值，則由上式推導出下列表達式，其中，避免結果發散的索引ωk表達式如式(7)所示：

(6)

(7)

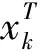
(8)

式中，U、V分別為兩相互正交矩陣；Δ為對角矩陣，經分解獲得兩正交矩陣U、V的首列，用前者完成初始字典內原子dk的更新，將后者與對角矩陣Δ(1，1)相乘后，通過所得乘積更新與替換xj，進而獲取新的稀疏字典。

(3)確立測量矩陣。架構高斯測量矩陣，降低稀疏矩陣表示信號維度，同時確保重構信號準度與約束等距條件成立。也就是說，在0～1的取值范圍中有一個常數δk，對于全部稀疏系數矩陣X來說，測量矩陣Φ可使下列不等式成立：

(9)

(4)建立聯合重構算法。通過融合同步正交匹配追蹤算法與學習訓練算法，建立聯合重構算法。先用前者算法重構所采集的穩態數據，再用后者算法更新稀疏字典。算法運行流程具體描述如下。

①初始化處理聯合重構算法的相關參數。對于初始殘差r0，其與第p個節點對應的殘差rp之間為相等關系；索引值ωk=0；索引集Λ0是空集；

②將初始信號矩陣Xn×s、初始字典ψn×n、測量矩陣Φn×n、最低重構信噪比SNRdef作為輸入項，其中，s是節點個數，且p={1，2，…，s}，數據長度是n，測量個數是m；

③建立傳感矩陣，得到下列表達式：

Am×n=ψm×n×Φn×n

(10)

④采用下列公式求解各行殘差rp與各列傳感矩陣Aq之間的二范數[9]總和：

(11)

根據取得的二范數總和極大值，保留與之對應的傳感矩陣列索引，將其與索引集融合后，得到新的索引集，如下所示：

Λr=[Λr-1ζp]

(12)

⑤經最小二乘算法[10]解得相關參數后，利用下列表達式更新殘差：

(13)

⑥采用下列計算公式分別解得重構的中間信號及其相對方均根誤差與重構信噪比：

(14)

(15)

(16)

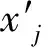
2 小波變換下電力系統穩態數據壓縮

基于邊緣計算所得的穩態數據融合結果，利用小波變換算法[11]按分辨率將其分解至各個尺度水平上，得到高頻系數與低頻系數，經閾值處理把相對小的高頻系數歸零，只留存低頻系數與具備信號特征呈現能力的高頻系數。從根本上實現整數到整數的變換，降低浮點計算步驟，使方法更適用于電力系統的實際應用。基于小波變換算法的重構壓縮共分為分裂、預測、更新等幾個階段，其原理如圖1所示。

圖1 重構壓縮原理示意Fig.1 Schematic diagram of reconstruction compression principle

已知偶數序列ej+1，奇數序列oj+1，則采用下列表達式描述小波分解過程：

(17)

式中，偶數序列ej+1=aj+1-U(bj+1)，奇數序列oj+1=bj+1-P(aj+1)。其中，aj+1與bj+1分別表示序列中的低頻系數與高頻系數，Y(bj+1)與P(aj+1)分別表示高頻系數的更新結果與低頻系數的預測結果。

由此推導出壓縮重構的信號表達形式：

(18)

式中，merge表示歸并排序算法[12]。

電力系統穩態數據信號的融合與壓縮方法實現流程如圖2所示。先利用邊緣算法融合穩態數據信號，再通過小波算法展開多尺度變換處理，經閾值處理高頻系數，采用無損編碼技術提升壓縮比。

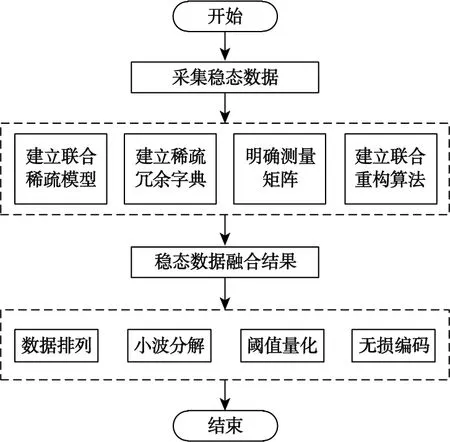
圖2 電力系統穩態數據信號的融合與壓縮流程Fig.2 Fusion and compression process of steady-state data signals in power system

4 電力系統穩態數據壓縮實驗分析

4.1 實驗準備階段

針對某電網公司的試運行電力系統進行靜態數據的壓縮試驗，驗證本文方法的可行性與適用性。在用電接口上接入EAC5000D型電能量采集裝置，采集研究對象的穩態數據，其采樣信號如圖3所示。采集過程中，采樣率50 kHz，初始電壓信號的采樣點個數36 000。

圖3 穩態數據采樣信號示意Fig.3 Steady-state data sampling signal schematic

為衡量數據壓縮效果，先采用融入了多種壓縮方式融合與張量Tucker分解的文獻方法以及本文方法，逐一壓縮采集到的靜態數據，觀察其重構信號與誤差信號波形；再利用數據壓縮空間占比、賦范均方誤差以及數據壓縮比率3個指標進行定量評估。

(19)

(20)

賦范均方誤差=

(21)

以上3個指標中，除了數據壓縮空間占比指標值與壓縮效果之間呈正相關之外，另外2個壓縮評價指標均與壓縮效果呈負相關，指標值越小，壓縮效果越理想。

4.2 穩態數據壓縮效果分析

不同方法的靜態數據壓縮重構信號與誤差信號分別如圖4、圖5、圖6所示。從信號波形圖中能夠明顯看出，對比文獻方法的重構信號，本文方法因采用邊緣算法融合了采集到的穩態數據，利用小波變換算法分解融合信號至各個尺度水平上，所以使最終壓縮信號與實際穩態數據采樣信號波形(圖3)具有更高的擬合程度。

圖4 基于多種壓縮方式融合的信號波形Fig.4 Signal waveform based on fusion of multiple compression methods

圖5 基于張量Tucker分解的信號波形Fig.5 Signal waveform based on tensor tucker decomposition

將不同方法的信號波形及其賦范均方誤差與數據壓縮比率評價指標結果(圖7)相結合，可以看出，本文方法因引用小波變換算法，從根本上實現了整數到整數的變換，大幅降低了浮點計算步驟，通過無損編碼技術提升壓縮比。因此，數據壓縮比率與賦范均方誤差2指標值均遠遠小于文獻方法的指標值。這說明本文方法能夠去除的冗余數據更多，且初始信號特征也得以更好保留，壓縮優勢顯著。

3.3 基于數據規格的穩態數據壓縮效果分析

為檢測數據大小對壓縮效果的影響，針對規格分別為64 kB、128 kB、256 kB、512 kB、1 MB的穩態數據，采用數據壓縮空間占比，評價不同方法的穩態數據壓縮效果。指標數據結果如圖8所示。

由此可以看出，本文方法通過閾值處理把相對小的高頻系數歸零，只留存低頻系數與具備信號特征呈現能力的高頻系數，因此，相比其他2種文獻方法的壓縮空間占比更大，壓縮效果更理想。

圖6 本文方法信號波形圖Fig.6 Signal waveform diagram of the method in this paper

圖7 賦范均方誤差與數據壓縮比率指標值Fig.7 Normed mean square error and data compression ratio index value

從本文方法的空間占比曲線走勢可知，隨著數據規格的增加，指標值有所下降，這表明該方法的壓縮效果與數據大小之間存在一定的相關性，可將其作為下一階段的研究重點，以應對信息時代電力系統海量的數據規模。

圖8 數據壓縮空間占比指標值Fig.8 Data compression space ratio indicator value

5 結論

電力系統是電網企業的關鍵組成部分。社會與科技飛快發展，智能化、信息化程度日益加深，隨著電網通信技術迅猛提升，數據傳輸規模日漸強大，促使數據壓縮逐漸演變成電力領域的熱點研究課題之一。為此，本文結合邊緣計算方法，構建出穩態數據壓縮方法。

由于本文的研究進程仍處于初始階段，因此，需進一步改進以下幾個方面：應針對穩態數據信號特點，嘗試更適合的稀疏方式，使稀疏更加高效，重構信號更加精準；本文僅探討了一種信號擾動情況，但現實應用中的穩態數據有多類畸變與擾動問題，應將其作為壓縮時的考慮因素，提升方法實用性；下一階段需繼續探討小波變換尺度問題，令小波基的選取不再僅憑先驗知識。本文研究成果將會為工業應用與學術研究帶來重大突破，為信息科學掀起一場變革浪潮。