從經歷到經驗 從簡模到精模
張蓉 高穎菁

【摘 要】數學模型是指針對或參照某種事物的特征或數量間的相依關系,采用形式化的數學語言,概括地或近似地表述出來的一種數學結構。在數學教學中,教師要教給學生已經建立的數學模型和建立數學模型的方法。重視數學建模,有利于提高學生的應用意識。本文以蘇教版數學六年級上冊“認識百分數”一課為例,由實際問題引導學生建立數學模型,然后進行模型的優化與應用,結合教學過程,淺談基于建模思想的教學實踐和反思。
【關鍵詞】數學 建模教學 模型思想
重視數學建模,有利于提高學生的應用意識。下面,筆者就結合蘇教版數學六年級上冊“認識百分數”一課,談一談模型思想教學的實施策略。
一、激趣引須,引發建模需求
模型思想的建立,是從現實生活或者具體情境中抽象出數學問題,然后對其進行必要的簡化。在課堂教學中,教師創設一個與學生息息相關的有趣情景,可以激發學生的學習興趣,引導學生從具體情境中抽象出數學問題,從而引發建立數學模型的需求。
例如,在教學“認識百分數”這節課時,教師以學生熟悉的光盤行動為主題,先出示幼兒園大班和中班各班的光盤情況。大班的三個班班級總人數相同,只需比較每個班的光盤人數,中班的三個班光盤人數相同,只需比較每個班的班級總人數,這樣,學生能快速順利地搶答出大班和中班的哪個班光盤情況更好。在此基礎上,出示小班光盤情況(如圖1):
師:選哪個班?請大家進行搶答。
(生答不出,想到可以比較光盤人數占班級總人數的幾分之幾,然后通分進行比較,從而選出了小2班是光盤情況最好的)
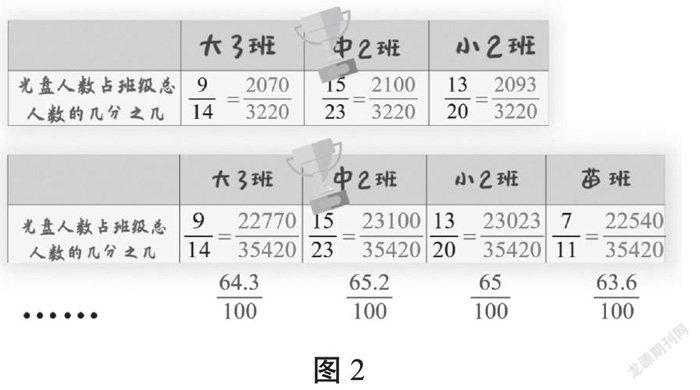
(再次PK,出示:大3班 9/14,中2班 15/23,小2班13/20)
(出示通分結果:大3班:2070/3220,中2班2100/3220,小2班2093/3220)
師:哪個班勝出?(中2班)
師:苗班的小朋友也想來比一比(苗班:7/11),現在哪個班勝出啦?公分母又要變化了!(出示通分結果:大3班22770/35420,中2班23100/35420,小2班23023/35420,苗班22540/35420)
師:哪個班勝出?(中2班)
師:現在還只是四個班在比較,如果全區的小朋友甚至全市的小朋友都來PK,那么公分母就會不停地變化。
師:統計人員也發現了類似問題,所以,他們想到把這些分數化成分母是100的分數,這樣會便于統計和比較。(PPT出示:大3班64.3/100,中2班65.2/100,小2班65/100,苗班63.6/100)
特級教師王凌曾經指出,情境創設是目前教學中的常用手段,一個好的情境應能與學習內容進行有效的結合,并且能有效地幫助學生促進理解。把與學生息息相關的生活實際問題帶入數學課堂,可以讓學生發現數學的有用之處。例題以選擇光盤情況最好的班級為切入口,借助學生已有的經驗——通分,讓學生選出光盤優勝班。接著,教師出示公分母很大的幾個分數,讓學生感受到,每比一次就通分一次,既難且繁,以前所學的知識不能很好地解決此類問題,從而順利地引出用分母是100的分數來表示的內容。強烈的視覺對比之下,學生能直觀體會到用分母是100的分數來表示統計結果更便于比較和選擇。(如圖2)
二、思考交流,初建數學簡模
對于一些數學概念的學習,很多學生停留在死記硬背的階段。大部分教師的日常教學都是直接由例題揭示概念,缺少了學生主動體會、探索的過程。概念雖然是定義式的,但概念的教學應該體現數學與生活的聯系,讓學生從生活中尋找實例,在充分的情景體驗之下,感悟概念數學模型的建立。
例如,在教學“認識百分數”一課時,教師讓學生搜集生活中常見的百分數,并在小組中交流每個百分數表示的意義。
生1:(衣服標簽)75%棉表示棉占這件衣服的75%。
生2:(手機電量)54%表示剩余電量占手機總電量的54%。
生3:(餐巾紙盒)100%原生木漿表示原生木漿占紙的100%。
(師分別板書)
在上一環節,學生感受到了用百分數表示一個數是另一個數的百分之幾便于比較。對于百分數,學生已有一定的生活經驗。因此這個環節,筆者先讓學生說一說生活中常見百分數所表示的意義,在具體情境下將生活經驗與數學概念相溝通,使生活情境得以數學化。數學模型的構建過程就是一個不停感知、體會、積累的過程。豐富的實際生活材料為百分數數學模型的構建提供了可能,雖然百分數的意義還未揭示,但是“百分數表示( ? )占( ? )的( ?)%”的數學模型已經潛移默化地在學生腦海中扎根。
三、歸納概括,建構數學中模
建立模型思想的起點是從現實生活中或者具體情境中抽象出數學問題并進行簡化。學生對數學模型思想的感悟過程,不僅是外顯的形式學習過程,還是深入體悟知識產生的過程,是經歷將實際問題“數學化”的過程。
例如,在教學“認識百分數”時,學生充分體會了生活中具體的百分數所表示的意義,并用規范的語言進行了表述。
(讓學生回顧剛剛的學習過程,觀察上述板書)
師:你覺得百分數表示什么?
生:表示一個量占另一個量的百分之幾。
師(引導揭示概念):表示一個數是另一個數的百分之幾的數,叫作百分數。
學生在上一環節已經充分體會到了百分數在實際生活情境中所表示的意義。這一環節主要是讓學生從剛剛的交流中,觀察、發現這些不同的百分數所表示的不同意義中相同的部分。數學模型的建立,正是要引導學生從生活中的問題原型出發,經歷觀察、比較、分析、抽象、概括等過程,去掉數學問題中不相同又非本質的東西,用精練的數學語言或者數學符號概括出數學模型。當學生能通過自己的感悟概括出百分數的意義時,學生也就完成了百分數概念的模型建構。
四、數據剖析,初次應用模型
數學來源于生活,又服務于生活。新課標指出,要讓學生親身經歷將實際問題抽象成數學模型并進行解釋與應用的過程。建立數學模型的目的是要通過應用數學模型解決問題,讓學生深切體會到數學的應用價值,激發學生對數學學習的興趣。
例如,在教學“認識百分數”這節課時,筆者引導學生應用已經建立的百分數概念的模型,理解實際問題中數據的含義,通過數形結合體會部分量與總體的關系,并且將建立的數學模型放到統計中,利用數學模型分析數據。
(一)用數學模型理解形中之數
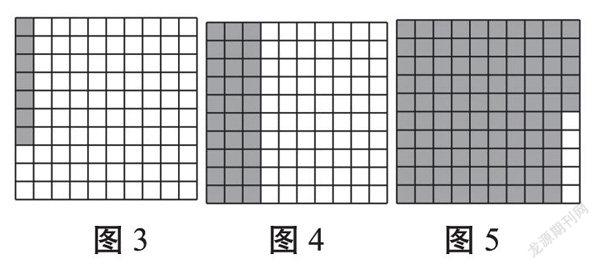
出示百格圖(涂色部分表示光盤人數,空白部分表示未光盤人數),讓學生分別填寫三張圖的情況并匯報。(如圖3、圖4、圖5)
師:觀察每張圖的涂色部分和空白部分,你有什么發現?
生:加起來等于100%。
師:希望在不久的將來,我們的光盤率可以達到多少呢?
生:100%。
這個環節把光盤情況與百格圖相結合,將實際情景抽象化的同時,直觀地讓學生體會到百分數表示兩個數之間的關系。在涂色部分變多的同時,表示光盤人數的百分數也越來越大,而且表示光盤和未光盤的百分數合起來就是100%。在這個環節中,教師讓學生利用數學模型理解數據含義,從而滲透部分量與總量之間的關系的知識內容。
(二)用數學模型分析統計數據
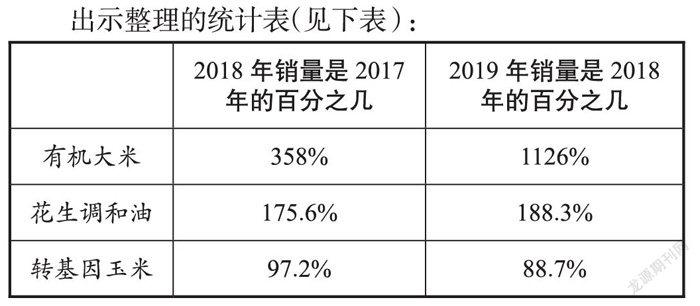
出示整理的統計表(見下表):
師:觀察這張統計表,你能獲得哪些信息?
(生分析表中信息)
師:糧油店的老板們要為“雙11”備貨,看著這張表,你有什么好的建議?
生1:多進有機大米,少進轉基因玉米。
生2:花生調和油也可以多進點。
師:通過統計數據,分析百分數的含義,還可以幫助我們進行合理的預測呢!
百分數是由數據的統計產生的。為了體現百分數對統計的作用,在這個環節,筆者設計了一張統計表,讓學生應用數學模型分析表中百分數所表示的含義。學生發現超過100%就說明銷量增長了,低于100%就說明銷量減少了。通過簡單的幾個百分數所表達出的豐富信息,學生體會到“百分數會說話”的特點。這個環節引導學生主動應用數學模型分析數據,不僅調動了學生學習的積極性,還提高了學生應用數學模型解決問題的能力。
五、反思優化,構建數學精模
學生在應用數學模型的過程中,可能會遇到一些困惑。教師幫助學生解決這些困惑,就能加深學生對數學模型的理解,從而多角度地優化已經建構的數學模型。
例如,在教學“認識百分數”時,教師引導學生體會兩個獨立的量之間用百分數表示的關系,用實際情境幫助學生區分百分數與分數之間的聯系和區別,優化數學模型。
(一)探究兩個獨立的量相比較
(課件出示,選擇合適的百分數填空)
某地區水稻田全年的實際產量是計劃產量的( ?)。
A.7% ? ?B.22% ? ?C.100% ? ?D.120% ? ?E.200%
生(依次選擇):100% 、120%、 200%。
師:為什么這里可以超過100%?
師(引導):這里是兩個獨立的量,實際產量可以比計劃產量多。
在這個環節之前,學生接觸的都是部分量占總量的百分之幾,是不大于100%的百分數。這個環節設計了讓學生選擇實際產量可能是計劃產量的百分之幾的題目,并讓學生思考:為什么這里可以超過100%?為了幫助學生理解,筆者設計了兩個直條表示實際產量和部分產量,與部分量占總量的情況區分開,使學生容易理解,通過實際情境加深了學生對“百分數表示一個數是另一個數的百分之幾”概念的理解,構建出更為精細的數學精模。
(二)探究分數和百分數之間的聯系與區別
出示一則數學日記:超市的月餅進行“買一送一”的促銷活動,相當于優惠了50/100。一個月餅的凈含量是30/100千克,媽媽吃了一個月餅的75/100就吃不下了。我想起老師教育我們要杜絕浪費,厲行節儉,就把剩下的吃掉了,吃完后又喝了20/100升水。
師:這里哪些分數可以用百分數表示?哪些不能?為什么?
生:50/100可以寫成50%,75/100可以寫成75%。
師:其他兩個為什么不能?
生:因為它們有單位,表示的是具體的量。
師(引導小結):百分數只能表示兩個數之間的關系,后面不能有單位。
雖然這個環節看似簡單,但在上課過程中筆者發現,有不少學生會把所有分數都改寫成百分數,這說明學生對于百分數意義的理解還未完全內化,對于百分數和分數的區別不夠清晰。因此,這個環節針對百分數與分數之間的聯系和區別再一次進行強化,以優化補充學生建構的百分數模型,使數學模型更為精細化。
六、經驗升華,貫通模型思想
師:誰能就這節課的收獲來介紹一下百分數?
生1:百分數就表示一個數是另一個數的百分之幾。
生2:百分數只能表示兩個數之間的關系,后面不能有單位。
……
課堂的最后讓學生對本節課所學內容進行回顧與總結,也是幫助學生再次梳理本課內容,感悟、貫通模型思想。
教師在日常教學中有意識地培養學生的模型思想,不僅能讓學生感受到數學是看得見、摸得著的,還能讓學生學會舉一反三,擁有較強的獨立學習的能力,利用模型思想去解決更多的數學問題,發掘數學的本質。

