低速磁浮線軌道鋼箱梁表面溫度分布及豎向撓度實測研究*

劉鳴博 葉 豐** 曾國鋒 龔俊虎

(1.同濟大學磁浮交通工程技術研究中心， 201804， 上海； 2.西南交通大學牽引動力國家重點實驗室， 610031，成都； 3.中鐵磁浮交通投資建設有限公司， 430060， 武漢∥第一作者， 碩士研究生)

國內外研究者對橋梁結構在太陽輻射作用下的溫度效應及其分析方法等做了大量研究。文獻[1]將橋梁結構溫度場的研究方法分為理論分析、數值模擬及試驗測試等3類；文獻[2]建立了上海高速磁浮示范運營線鋼箱梁的日照溫度場模型，以縮尺模型的實測數據對模型進行驗證后，計算了不同支承形式鋼軌道梁的溫度變形；文獻[3]用傅里葉曲線擬合并研究均勻溫度與波動溫度的時程曲線，得到磁浮混凝土軌道梁溫度場的時變規律；文獻[4-6]以實際測試的數據為基礎，利用威布爾和正態分布的加權模型擬合實測溫差的統計結果，并據此推算最不利溫差值；文獻[7]引入赤池和貝葉斯信息判別準則，確定最優高斯分量數，建議采用分段函數來描述鋼箱梁日溫度變化特征。

與其他城市軌道交通制式相比，低速磁浮軌道梁在溫度梯度作用下的撓度限值更為嚴格，目前尚無明確的針對低速磁浮軌道梁的溫度梯度荷載規定或可借鑒的相關規范。CJJ/T 262—2017《中低速磁浮設計規范》中規定梁體在溫度梯度作用下跨中豎向撓度的容許值為計算跨度的1/6 200，但未明確該規范值對應的溫度梯度荷載作用。本文以上海臨港低速磁浮線鋼箱梁的表面溫度監測數據為研究案例，對低速磁浮鋼箱梁的表面溫度分布及豎向撓度進行分析。

1 案例鋼箱梁的現場測試概況

上海臨港低速磁浮線的鋼箱梁結構形式如圖1所示。兩側F軌為列車無接觸運行時的軌道，因其橫斷面形狀類似字母F，故以“F軌”代稱。鋼軌枕將F軌連接成軌排，軌排通過鋼箱梁頂面間隔布置的承軌臺與鋼箱梁連接。列車運行時，荷載由F軌向下依次傳遞至方鋼管、混凝土承軌臺以及鋼箱梁上。鋼箱梁表面無鋪裝保護，軌排可能會對鋼箱梁頂面的日照有少許遮擋作用。

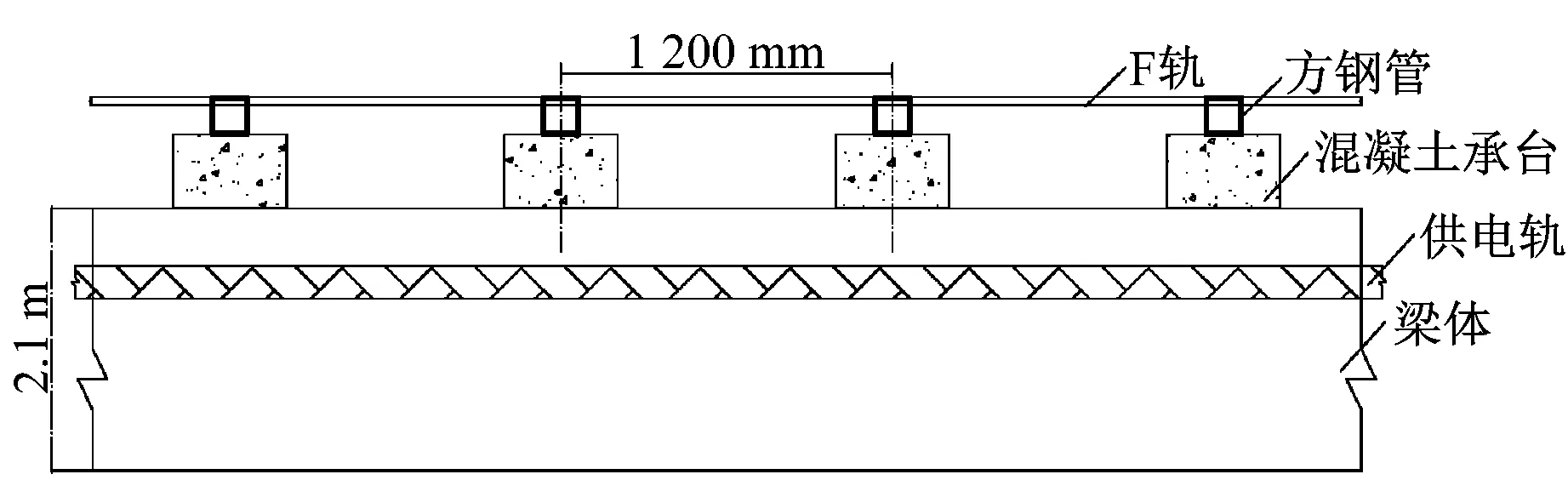
圖1 上海臨港低速磁浮線鋼箱梁結構

本文選取上海臨港低速磁浮試驗線上47#～48#墩柱之間的鋼箱梁進行現場溫度測試。該鋼箱梁為簡支結構，跨度為25.0 m，高度為2.1 m。現場溫度測點布置如圖2所示，其中：A2-B2斷面為跨中斷面，被命名為斷面2;其兩側的豎向斷面A1-B1、A3-B3分別被命名為斷面1和斷面3。

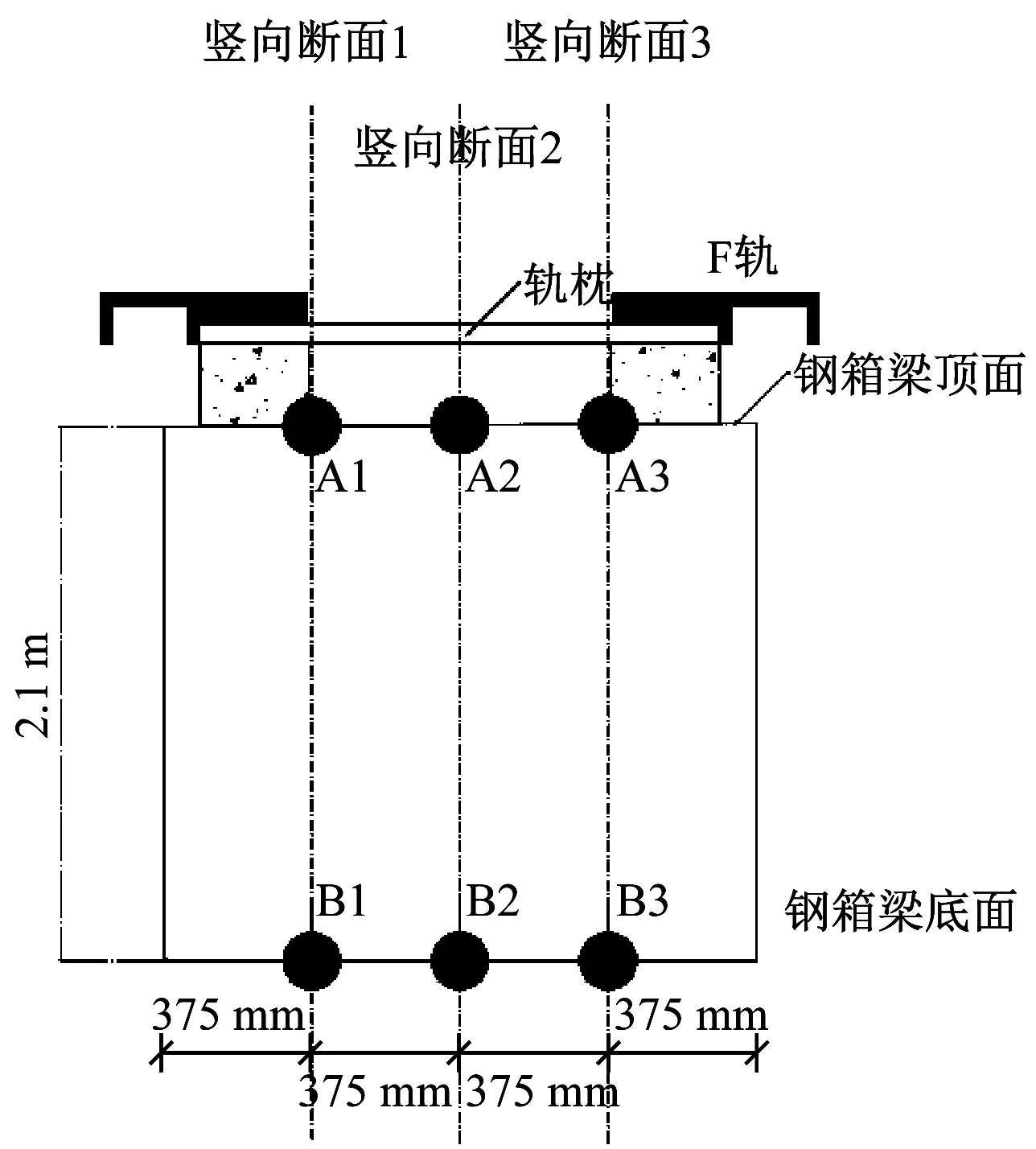
圖2 鋼箱梁測點布置示意圖Fig.2 Diagram of steel box girder measurement points arrangement

2 豎向表面溫度差分析

2.1 豎向表面溫度差極值分析

對2020-07-30至2021-02-20期間該鋼箱梁的表面溫度進行監測，采樣的時間間隔為15 min/次。選取2020-07-30至2020-09-03、2021-01-22至2021-02-20期間的監測數據作為鋼箱梁表面溫度差的統計分析樣本。

將頂面測點監測值減去對應豎向斷面上底面測點的監測值，得到的差值定義為該斷面的豎向表面溫度差。既有的研究表明，鋼箱梁的正、負溫差的統計特性具有較大的差異，因此本文對正、負溫差進行了分類分析，設Tj為對應的豎向斷面(j=1、2、3)的溫度差樣本，ΔTj為對應的溫度差樣本，ΔTj,p為Ti的正溫度差，ΔTj,n為Tj的負溫度差。在3個確定的豎向斷面溫度差的基礎上，為反映鋼箱梁頂、底面間整體的溫差特征，將梁頂面3個測點監測值取均值，減去同一時刻梁底面3個測點的平均監測值，將差值定義為平均表面溫度差。將平均表面溫度差樣本表示為Ta，將平均表面正、負溫度差樣本分別表示為ΔTa,p和ΔTa,n。

圖3為典型樣本下鋼箱梁各斷面表面溫度差及平均表面溫度差的時程變化情況，可以看出：不同的溫度差樣本在時程波形上相似，但數值有所差異。T2的表面溫度差變化最大，Ta與T3的表面溫度差較為接近。

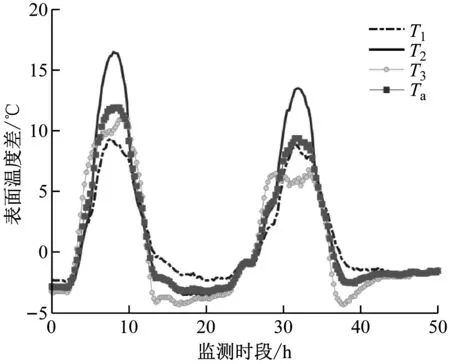
圖3 典型樣本下鋼箱梁豎向表面溫度差時程曲線

統計各斷面監測樣本的表面正、負溫度差極值，結果如表1所示。由表1可知：① 豎向正溫度差最大值為19.8 ℃，發生在斷面2；負溫度差最大值為-7.6 ℃，發生在斷面1；斷面3的表面溫度差的極值統計結果與平均表面溫差接近；② 4個溫度差樣本的表面負溫度差絕對值均在4 ℃以上。

表1 各監測斷面表面溫度差樣本極值

2.2 豎向表面溫度差概率統計

過往的研究表明，威布爾分布模型、正態分布模型與鋼箱梁的實測溫差概率統計特征接近[4-6]。因此，本文采用多概率密度函數加權的形式擬合豎向表面溫度差。通過觀察實測數據的概率統計特征，將鋼箱梁的表面溫度差數據拆分為正、負溫差樣本，分別選取雙威布爾分布模型、雙正態分布模型、威布爾分布和正態分布加權模型進行比選，采用最小二乘法擬合確定最佳的參數取值，通過比較不同擬合結果的殘差平方和得到最優的概率模型。圖4為平均表面正、負溫度差的擬合結果。

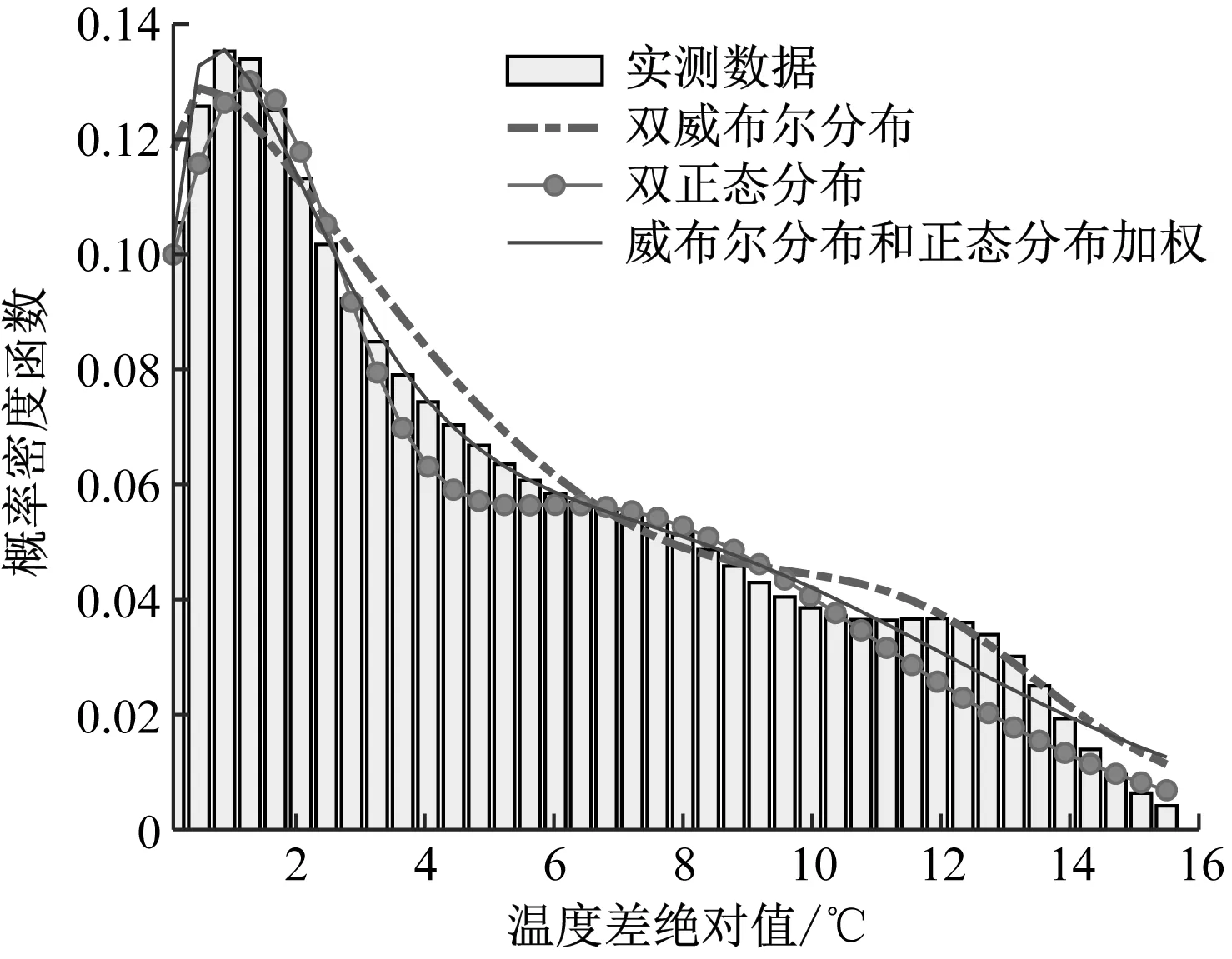
a) 表面正溫度差擬合結果

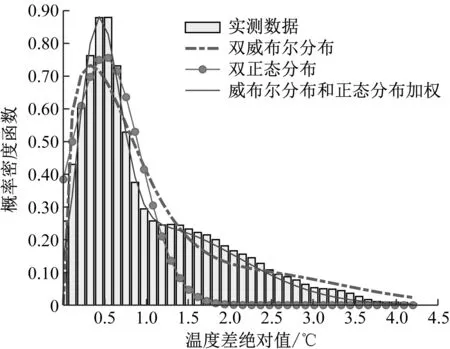
b) 表面負溫度差擬合結果圖4 平均表面正、負溫度差擬合結果對比Fig.4 Fitting results comparison between surface positive and negative temperature difference

由計算結果可知：在描述各個樣本的豎向表面溫度差時，威布爾分布與正態分布加權模型的擬合效果最優，其總體的殘差平方和最小。故最終選用威布爾分布與正態分布加權模型來描述低速磁浮軌道鋼箱梁表面正、負溫度差的概率統計特征，其計算式為：

g(ΔTi,p)=γ1W(ΔTi,p,α1,β1)+γ2N(ΔTi,p,μ1,λ1)

(1)

g(ΔTi,n)=ρ1W(ΔTi,n,α2,β2)+ρ2N(ΔTi,n,μ2,λ2)

(2)

式中：

g(ΔTi,p)、g(ΔTi,n)——分別為鋼箱梁表面正、負溫度差的概率密度模型；

β1、β2——威布爾分布的尺度參數；

μ1、μ2——正態分布的均值；

λ1、λ2——正態分布的方差；

α1、α2—— 威布爾分布的形狀參數；

γ1、ρ1——威布爾分布的權重參數；

γ2、ρ2——正態分布的權重參數；

W(ΔTi,p,α1,β1)——變量為ΔTi,p、形狀參數為α1、尺度參數為β1的威布爾分布函數；

N(ΔTi,p,μ1,λ1)——變量為ΔTi,p、均值為μ1、方差為λ1的正態分布函數；

W(ΔTi,n,α2,β2)——變量為ΔTi,n、形狀參數為α2、尺度參數為β2的威布爾分布函數；

N(ΔTi,n,μ2,λ2)——變量為ΔTi,n、均值為μ2、方差為λ2的正態分布函數；

ΔTi——豎向表面溫度差樣本，包括ΔT1、ΔT2、ΔT3、ΔTa。

式(1)、式(2)滿足γ1+γ2=1，ρ1+ρ2=1。式(1)中各參數的估計值如表2所示，式(2)中各參數的估計值如表3所示。

2.3 豎向表面溫度差標準值分析

在重大工程的設計施工中，往往要計算具有一定重現期的標準值。氣象研究中對重現期的計算一般轉化為出現概率的計算，重現期為R年的極端值估計以1/(nR)對應的分位點處的數值表示，其中n為理論年樣本總量。根據上文極端值分析的結論，本文偏保守地采用斷面2對應的豎向表面正、負溫度差樣本的概率統計模型，用以計算溫度差標準值的最大值和最小值。其概率分布函數可表示為：

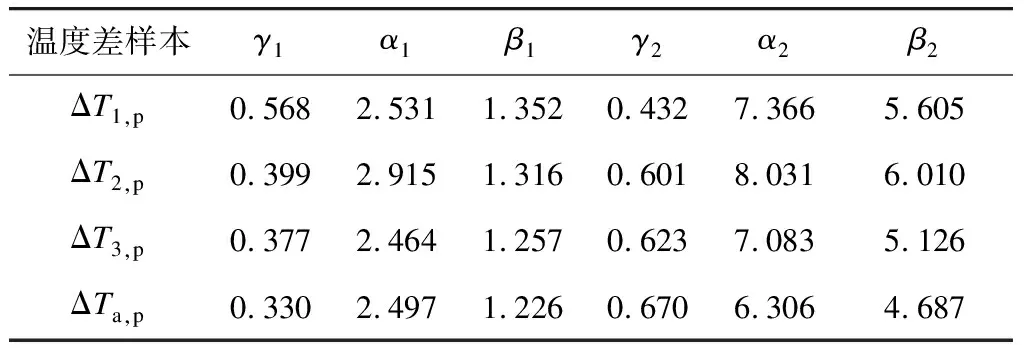
表2 正溫度差擬合參數估計值

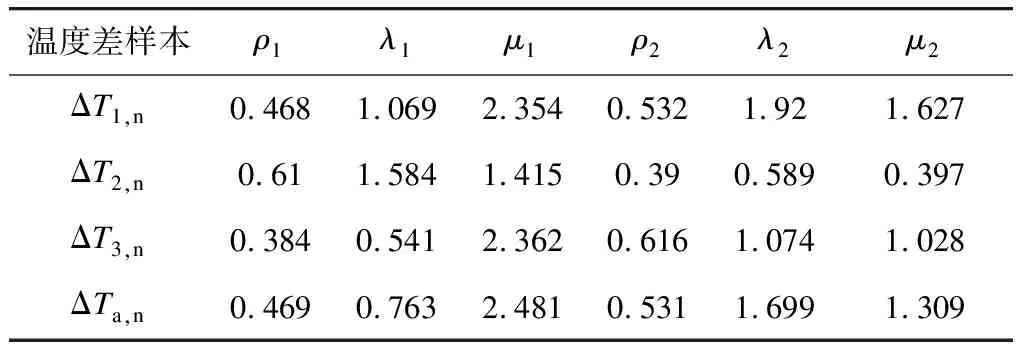
表3 負溫差擬合參數估計值

F(ΔT2,p)=γ1FW(ΔT2,p)+γ2FN(ΔT2,p)

(3)

F(ΔT2,n)=ρ1FW(ΔT2,n)+ρ2FN(ΔT2,n)

(4)

式中：

F(ΔT2,p)、F(ΔT2,n)——分別為斷面2的正、負溫差變量的概率分布函數；

FW(ΔT2,p)，FW(ΔT2,n)——分別為變量是ΔT2,p、ΔT2,n的威布爾概率分布函數；

FN(ΔT2,p)、FN(ΔT2,n)——分別為變量是ΔT2,p、ΔT2,n的正態概率分布函數。

參照歐洲結構設計標準的相關規定，采用具有50年重現期(R=50)的溫度差特征值作為標準值，選取數據的采樣頻率為15 min/次，則1 d的總采集次數為96次。取1年為365 d，故n=35 040。據此可計算得鋼箱梁表面的正溫度差標準值為29.2 ℃，負溫度差標準值為-10.2 ℃。

3 等效線性溫差與實測溫差的關系分析

鋼箱梁的豎向表面溫度差的主要影響因素為日照。為減小降雨、強風等復雜天氣因素的影響，本文選取監測期間晴好天氣的溫度及梁底豎向撓度數據的典型樣本，如圖5所示。

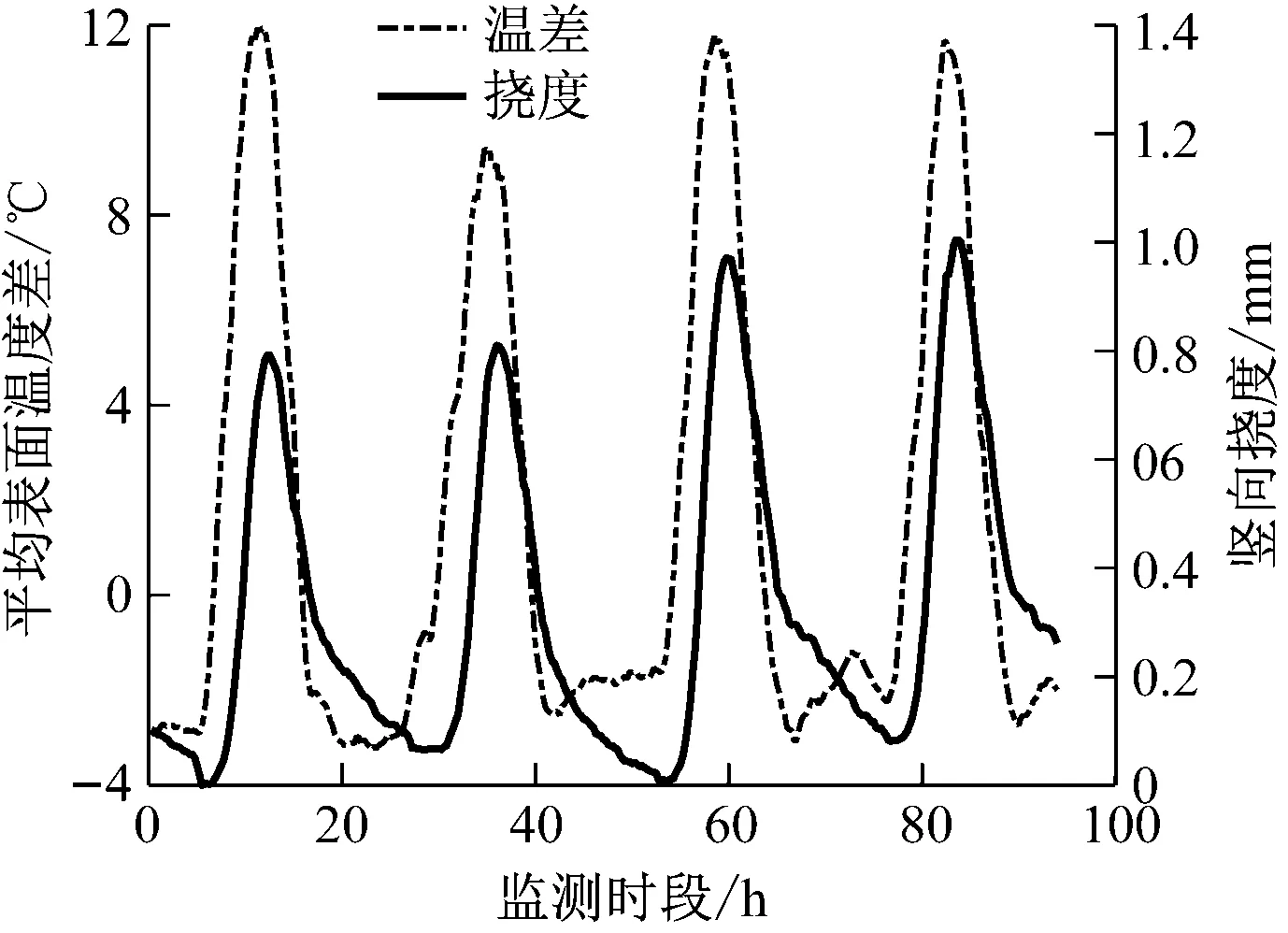
圖5 典型樣本下豎向撓度及平均表面溫度差監測數據

由圖5可知，鋼箱梁的豎向表面溫度差與梁底撓度之間存在較強的相關性，撓度與等效線性溫差的換算關系式為：

(5)

式中：

Δtmax——撓度等效線性溫差，℃；

h——鋼箱梁的高度，m；

Δftmax——鋼箱梁跨中豎向撓度值，m；

L——鋼箱梁的長度，m；

θ——線膨脹系數，1/℃。

由圖6的結果觀察可知，實測溫差與撓度的等效線性溫差之間呈帶狀分布，基本可以認定鋼箱梁的豎向表面溫度差與梁底撓度的等效線性溫差之間服從線性關系。考慮工程適用性，以線性模型描述鋼箱梁表面的實測溫度差與撓度等效線性溫差間的關系，其計算式為：

ΔTequ=kΔTa+b

(6)

式中：

ΔTequ——與實測撓度值對應的等效線性溫差；

k、b——待定系數。

通過最小二乘法求解得：k=0.12，b=-0.16。

由擬合結果可知：① 大部分實測值與擬合值之間的殘差絕對值在1 ℃以內，且基本呈帶狀分布于擬合曲線的兩側；② 實測數據與擬合曲線之間的擬合殘差絕對值最大值為2.7 ℃，由此引起的豎向撓度推算值的偏差對于低速磁浮線而言仍需要加以重視。為保證按此關系式計算的撓度推算值具備一定的安全余量，以覆蓋100%的數據點為標準，調整參數b的取值至2.62，擬合得到的上限曲線如圖6所示。

圖6 實測數據散點分布與擬合曲線Fig.6 Scattered distribution and fitted curve of the measured data

由此可推算得到等效線性溫差的估計值區間及等效撓度值的可能取值區間。結合上文得到的豎向表面溫度差標準值，對等效溫差極端值對應的豎向撓度進行估算，并與規范限值進行對比，如表4所示。由表4可知：① 針對高度為2.1 m的簡支鋼箱梁，由實測數據推算得到的50年重現期溫度梯度產生的撓度標準值，滿足中低速磁浮規范的要求；② 磁浮鋼箱梁的豎向負溫度差較大，其豎向負撓度不可忽略。

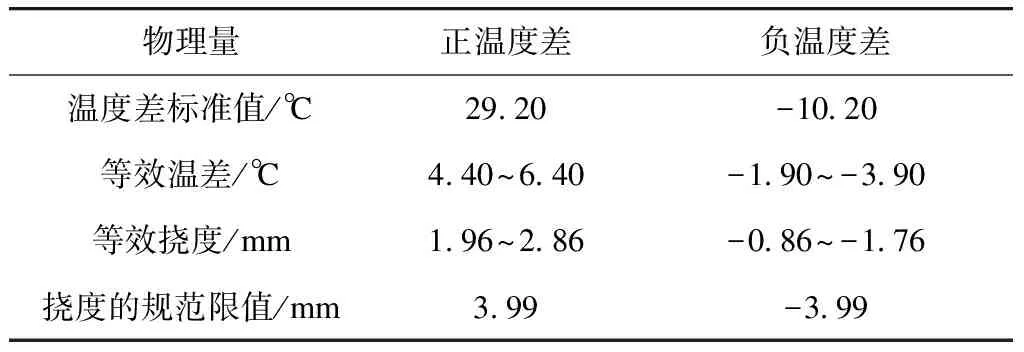
表4 溫度差標準值及估計撓度值

4 結語

本文以上海臨港低速磁浮試驗線上的鋼箱梁表面溫度分布實測數據為案例，初步研究了鋼箱梁表面溫度差的概率分布特性和等效線性溫差與實測溫差間的關系，得到以下結論：

1) 可以通過威布爾分布與正態分布加權模型來描述低速磁浮鋼箱梁頂面、底面的表面溫度差概率密度特征。根據概率模型推算出具有50年重現期的鋼箱梁豎向表面正溫度差標準值為29.2 ℃，負溫度差標準值為-10.2 ℃。

2) 本文主要考慮日照導致的溫差影響。低速磁浮鋼箱梁表面豎向撓度的等效線性溫差與實測豎向表面溫度差之間可以通過線性模型描述，并可通過包絡的方式得到鋼箱梁表面豎向表面溫度差所對應的等效撓度取值范圍。其中：正向(豎向向下方向)撓度的取值范圍為1.96～2.86 mm，負向(豎向向上方向)撓度的取值范圍為-0.86～-1.76 mm。

3) 因樣本數量和測試對象具有局限性，本文針對低速磁浮鋼箱梁溫度場分布和效應的實測分析尚處于初步探索階段。未來如能有更多試驗梁的實測數據，必將有助于更好地總結規律，為低速磁浮鋼箱梁結構設計提供參考。