某型高速列車車廂連接處脈動壓力的預測與控制*
張文敏 李啟良 賈尚帥 韓鐵禮 王毅剛
(1.中車唐山機車車輛有限公司技術研究中心, 063035, 唐山; 2.同濟大學上海地面交通工具風洞中心, 201804, 上海∥第一作者, 工程師)
我國是世界上高速鐵路發展速度最快、規模最大的國家。高速列車以超過300 km/h的速度運行時,列車的轉向架、受電弓和車廂連接處會產生強烈的氣動噪聲,嚴重影響了車內乘客的乘坐舒適性,因而長期受到廣泛關注。
車廂連接處是高速列車降噪隔振的薄弱部位,車外氣流產生的氣動噪聲較易通過車廂連接處進入車內。目前,針對車廂連接處噪聲的研究,大多基于壓縮比例和簡化的車廂連接處,采用試驗與仿真方法,圍繞噪聲產生機理及其控制開展。文獻[1]通過測量以300 km/h運行的高速列車車內噪聲發現,車廂連接處的測點總聲壓級比車廂中央處的測點高14.6 dB,比車廂兩端轉向架上方車內測點約高2.0 dB。文獻[2]給出法國TGV(高速鐵路)系統的列車以350 km/h運行時,其車廂連接處外部測點噪聲量值和峰值頻率(76 Hz、196 Hz和276 Hz)的產生原因。文獻[3]基于車廂端部二維空腔模型,研究了車廂端部上部倒角、上下同時倒角對于氣動噪聲的影響,發現設置車廂端部上端倒角可明顯降低下游氣動噪聲。在平順、光滑車廂連接上端圓角的基礎上,再平順、光滑下端的圓角,其降噪效果并不明顯。文獻[4]基于1∶8壓縮比例設置了3節編組列車模型,研究了高速列車在350 km/h速度下全包風擋與半包風擋對車廂連接處氣動噪聲的影響。該研究發現,采用全包風擋時,列車運行方向聲壓級最大降幅為3.1 dB,橫向聲壓級最大降幅為3.0 dB,垂向聲壓級最大降幅為2.4 dB。文獻[5]采用非線性聲學求解方法和FW-H方程獲得車廂連接處近場和遠場特性,發現車廂連接處呈現開式空腔噪聲特征,存在42 Hz共振峰值,總聲壓級與車速的5次方成正比。在此基礎上,提出并評估了半包風擋和全包風擋的控制方案。文獻[6]提出了一種基于貓頭鷹無聲飛行仿生學的氣動噪聲分析與設計方法,確定湍流強度最小的關鍵形態參數,以用于車廂連接處噪聲控制,從而達到較好的降噪效果。但是,針對車廂連接處的實車結構提出解決車廂連接處具體噪聲問題的有效措施并不多,而基于射流的主動流動控制尚未涉及。
為此,本文以某型高速列車車廂連接處的噪聲問題作為案例進行研究。該列車運行到350 km/h時,靠近第5節和第6節車廂連接處的乘務員室測點在中心頻率為40 Hz時所對應的聲壓級高達105 dB,遠大于其他頻率的聲壓級,嚴重影響了乘務員的乘坐舒適性。本文通過試驗和數值仿真手段找出車廂連接處噪聲的產生原因,在此基礎上評估基于波浪板的被動流動控制和射流的主動流動控制的效果,進而解決該噪聲問題。
1 脈動壓力預測
1.1 建立模型與體網格
目前線路上運行的高速列車通常為8節編組或16節編組,車長L超過200 m,車寬W約為3.5 m,車高H約為4.0 m。對如此大尺寸的高速列車進行實車脈動壓力預測與控制,保守估計所建立的列車模型的體網格數將超過10億個。為解決網格數過大、計算時間過長的問題,本文采用子域法,對實車車廂連接處的脈動壓力進行計算。所謂子域法,是指僅選取整車計算的一部分,并在此基礎上創建較小的計算域,如圖1所示。已有對實車頭型的研究表明[7],子域法得到測點和截面的平均流場和脈動流場特性與整車基本相同。本文所研究的車廂連接處也有類似的結論,受篇幅所限,不再贅述。

a) 8車編組高速列車模型
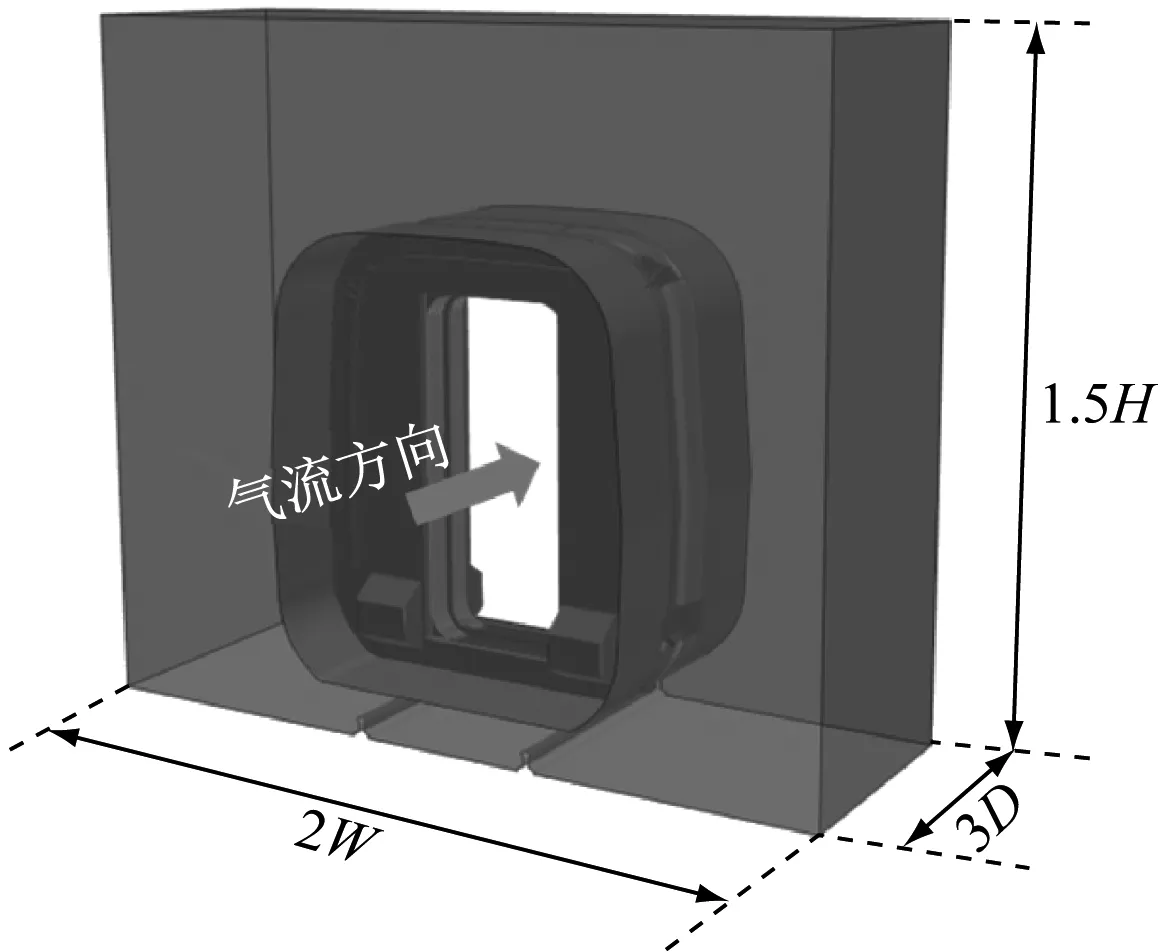
注:D為車廂端墻間距,約為0.7 m。 b) 第5節和第6節車廂連接處圖1 基于子域法建立的車廂連接處模型Fig.1 Model of inter-coach based on subdomain method
如圖1所示,模型的子域長、寬和高分別為3D、2W和1.5H。為了盡可能真實地模擬車廂連接處的氣動特性,除部分小孔洞外,模型幾乎保留了列車內、外風擋的所有細節。所有表面均劃分為三角形網格,其中:外風擋網格的基本尺寸為8 mm,最小為2 mm;內風擋和端墻等部件的網格尺寸為8 mm;車身等較大表面的網格尺寸為16 mm;計算域的網格最大尺寸為32 mm。所有表面共生成了280萬個面網格。
在此基礎上,使用STARCCM+軟件的Trimmer+layer策略生成計算域的體網格。對外風擋的四周進行網格加密,網格尺寸為8 mm。為了有效捕捉車廂連接處上、下缺口射流剪切層渦流的變化情況,對該區域進行網格細化,網格尺寸為4 mm。網格的加密位置如圖2所示,其中:圖2 a)標注為6-1等8處為外風擋所在加密區;圖2 b)標注為3-1等4處為上、下缺口所在加密區。
為了更好地模擬壁面邊界層流動,模型生成了第1層為0.025 mm的邊界層網格,首層網格對應量綱為一的壁面距離約為2,滿足延遲分離渦 (iDDES) 模型[8]對近壁網格的要求。模型中,除地面和軌道外的所有壁面均生成6層邊界層網格,網格尺寸的增長率為1.2。整個計算域共生成約3 100萬個體網格。
使用子域法進行脈動壓力計算時,不應直接在進口處給定均勻來流的邊界條件,而應將實車測試得到對應截面的速度、壓力、湍動能和耗散率等作為邊界條件。為此,在參考TB/T 3503.4—2018《鐵路應用空氣動力學 第4部分:列車空氣動力學性能數值仿真規范》的基礎上,本文建立了8節編組高速列車的實車氣動仿真模型。該模型含頭型、平直段、受電弓、轉向架、軌道等結構部件。整個模型面網格總計約650萬個。分別對所關注的車廂連接處進行網格加密,加密區域的網格尺寸為32 mm。除地面和軌道外,所有壁面均生成5層邊界層網格,網格尺寸的增長率為1.2,首層網格對應量綱為一的壁面距離約為100,滿足SSTk-w(剪切應力傳輸) 模型[9]對近壁網格的要求。整個計算域共計生成約1.2億個體網格。
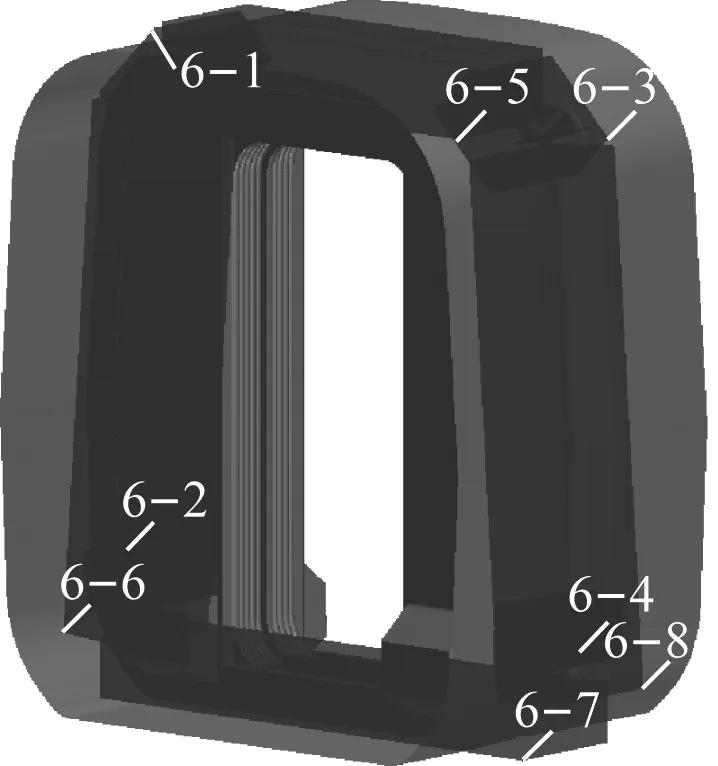
a) 外風擋加密區
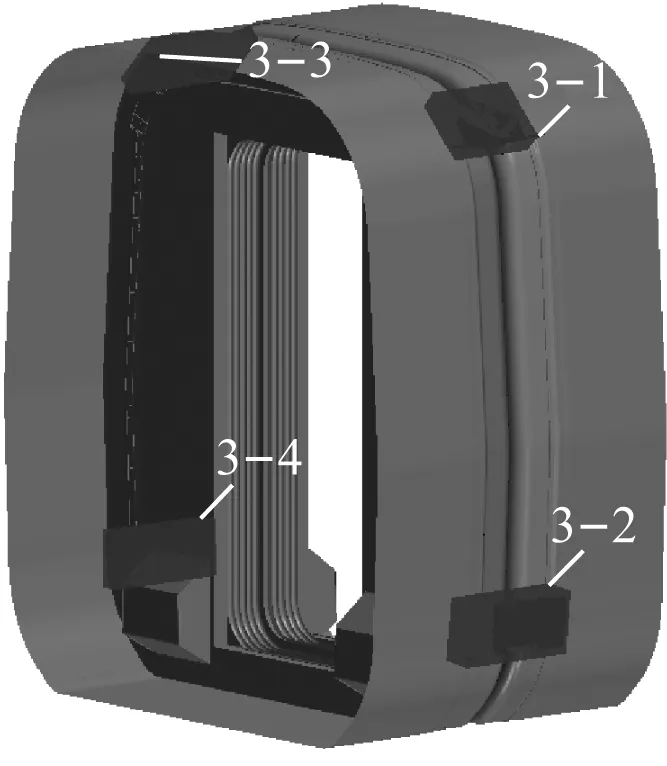
b) 上、下缺口加密區圖2 對車廂連接處外風擋區域的體網格加密位置Fig.2 Densifying volume mesh of the outer windshield region of the inter-coach
設定子域的進口為速度入口,并指定速度為350 km/h。地面和軌道為移動壁面,其移動速度也為350 km/h。車輪為旋轉壁面,設定角速度為214 rad/s,與之對應的輪邊線速度也為350 km/h。經穩態迭代3 000步后,計算結果收斂。在此基礎上,輸出子域對應截面的速度、壓力、湍動能和耗散率。
1.2 計算流程設置
子域的進口、兩側和頂面均指定為速度邊界,導入由整車模型輸出對應截面的速度、湍動能和耗散率。出口指定為壓力邊界,導入由整車模型輸出對應截面的壓力、湍動能和耗散率。地面和軌道給定為移動邊界,移動速度為350 km/h。
采用STARCCM+軟件的分離式求解器進行計算。參考TB/T 3503.4—2018的建議方法,并結合本研究,對計算流程設定如下:① 首先采用不可壓SSTk-ω模型迭代1 500步,然后更換成可壓SSTk-ω模型繼續迭代1 500步,以得到穩定的流場;② 選用iDDES進行非定常計算。由于車廂連接處的脈動壓力主要發生在幾十赫茲的低頻段,為了在有限的計算資源和較短的計算時間內能夠采集到足夠長的壓力信號,將時間步長設為0.002 s;③ 采用隱式計算方法,以避免產生時間步長對應的柯朗-弗里德里希斯-列維數大于1的情況發生,計算的時間和空間離散格式均為二階;④ 當非定常計算物理時間達到2 s時,發現監控點的脈動壓力達到動態平衡;⑤繼續進行非定常計算,并開始采集車廂連接處的表面壓力和空間壓力,采集時間為2 s。采集得到的數據將用于分析車廂連接處的脈動壓力特性。
1.3 計算結果分析
如圖3所示,在上、下缺口分別以150 mm間距創建3個空間測點,分別依次命名為P1-1、P1-2和P1-3,P2-1、P2-2和P2-3。其中:P1-1和P2-1分別靠近上、下缺口前端;P1-3和P2-3分別靠近上、下缺口末端。
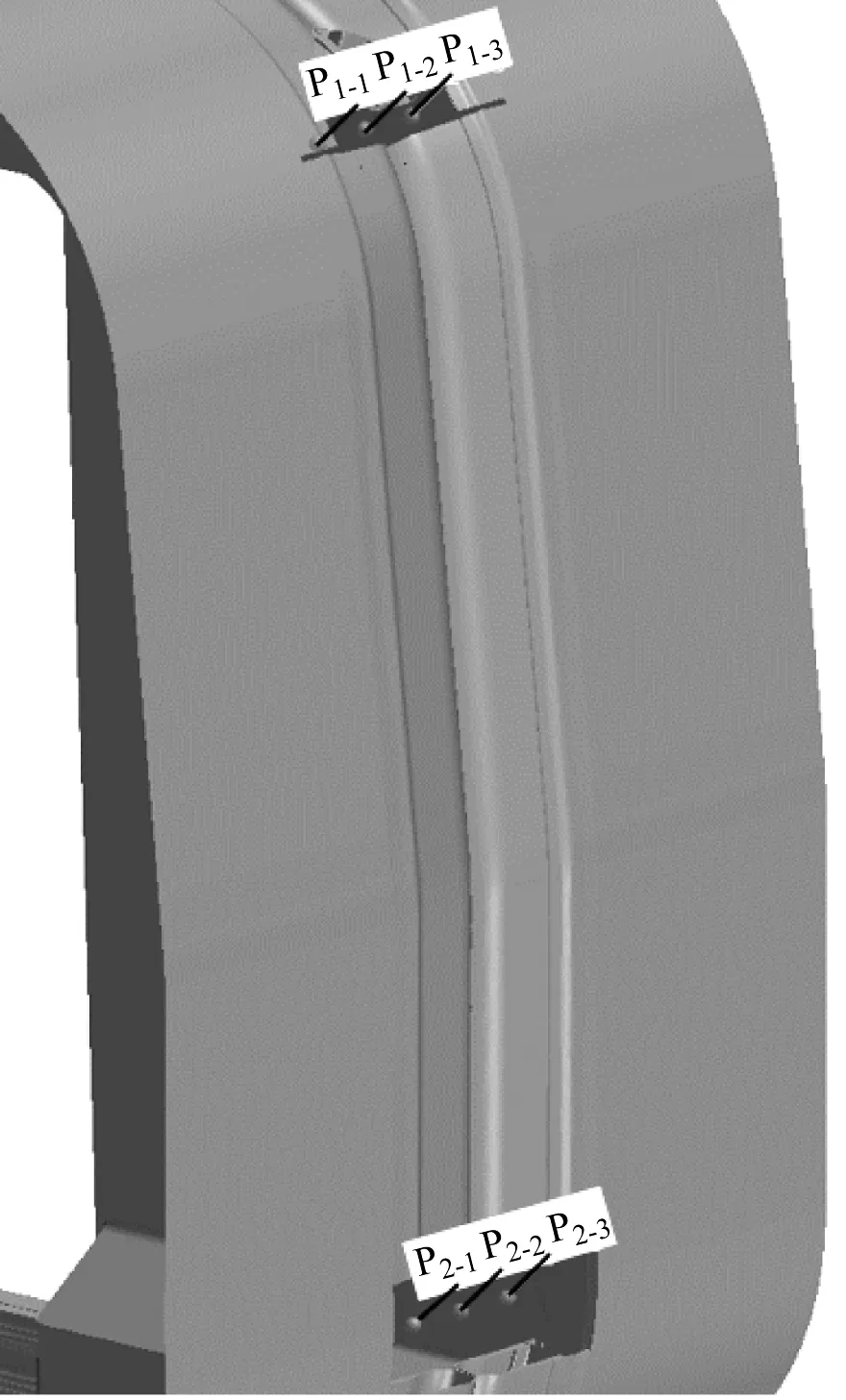
圖3 車廂連接處測點布置圖Fig.3 Layout of inter-coach test points
圖4為各測點的壓力功率譜密度圖。從圖4可以看出,壓力脈動主要能量集中在50 Hz以下。P1-1的壓力峰值小于P1-3的壓力峰值,這是由于車廂連接處長度與深度的比值較小,氣流從前端分離,渦流逐漸向末端發展和擴散,呈現出開式空腔的流動形態。P1-3分別在頻率為24 Hz、38 Hz和45 Hz時出現明顯的峰值,但P2-3僅在39 Hz時出現明顯尖峰。缺口區域氣流分離形成的射流剪切層雖然存在多個頻率成分,但并非每個頻率都會引起強烈的氣動噪聲,只有那些自身能量大且與聲腔模態頻率一致或接近的頻率才會因共振而產生氣動噪聲問題。
提取車廂連接處端墻和內、外風擋形成的聲學空腔區域并建立聲學網格,使用ACTRAN軟件對此區域進行聲學模態計算。聲學模態計算的最高頻率與流場計算的最高頻率相同,均為250 Hz。為了保證最高頻率對應波長有20個節點,模型的面網格和體網格最大尺寸均為68 mm,總聲學網格數約為14萬個。經計算,該聲學空腔的1~5階模態頻率依次為24 Hz、40 Hz、58 Hz、75 Hz和96 Hz。通過對比射流剪切層頻率和聲學模態頻率可知,40 Hz附近的射流剪切層頻率會引起車廂連接處的共振,進而產生強烈的氣動噪聲。因此,乘務員室的噪聲問題主要是車廂連接處發生了共振,共振頻率在40 Hz附近。后續的優化重點為降低40 Hz附近的脈動壓力。
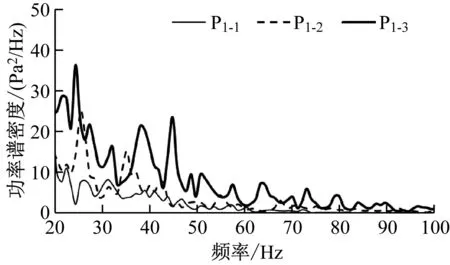
a) 上缺口測點
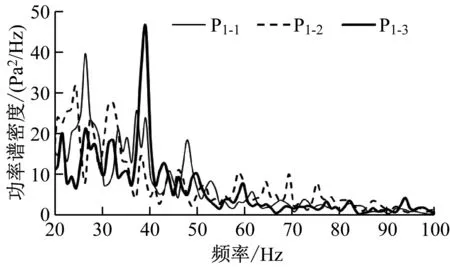
b) 下缺口測點圖4 各測點的功率譜密度-頻率曲線Fig.4 Power spectral density-frequency curve of each test point
2 脈動壓力控制
2.1 控制方案
2.1.1 波浪板控制方案
將上文所述的尚未采取控制措施時的模型定義為基礎模型。當前脈動壓力控制主要為外形優化、被動流動控制和主動流動控制。在本車型車廂連接處通過外形優化來控制脈動壓力,其控制效果不大。考慮到車廂連接處與轉向架艙都有類似的空腔結構,結合近年在1∶3和1∶8壓縮比例下高速列車轉向架氣動噪聲控制的風洞試驗所積累的經驗,以及本車廂連接處具體結構,確定在上、下缺口兩端采用波浪板進行車廂連接處的脈動壓力控制。波浪板向外傾斜5°;下缺口板的長度和寬度分別為217 mm和281 mm,波高和波距分別為50 mm和70 mm;上缺口梯形板的短邊和長邊的長度分別為127 mm和229 mm,梯形板高為105 mm,波高和波距分別為50 mm和72 mm。
2.1.2 射流控制方案
主動射流近年來被嘗試用于航空領域的氣動噪聲控制,但目前并未應用于高速列車領域中。為了評估射流在車廂連接處脈動壓力控制的效果,本文嘗試在上、下缺口兩端布置射流器,以滿足高速列車頭尾互換的運行工況。上、下缺口射流器的寬度分別為132 mm和302 mm,高度均為20 mm。模擬時采用105 km/h(約0.3倍車速)的射流速度,射流方向與氣流方向相同[10]。
2.2 控制效果分析
分別選取P1-3、P2-3,對比2個方案下各測點的壓力功率譜密度變化情況,如圖5所示。從圖5中可知,采用波浪板方案后,多數頻率下所對應能量均有顯著降低。對以40 Hz為中心頻率、帶寬36~45 Hz各測點的脈動壓力總能量進行計算,發現上缺口測點的脈動壓力總能量由152 Pa2降至105 Pa2,下缺口測點的脈動壓力總能量由171 Pa2降至71 Pa2;射流方案的降噪效果更好,開啟射流后,上、下缺口測點的脈動壓力總能量分別降至1 Pa2和15 Pa2。
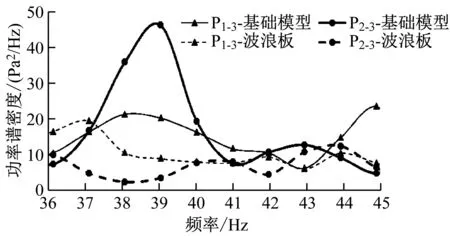
a) 波浪板方案與基礎模型的對比
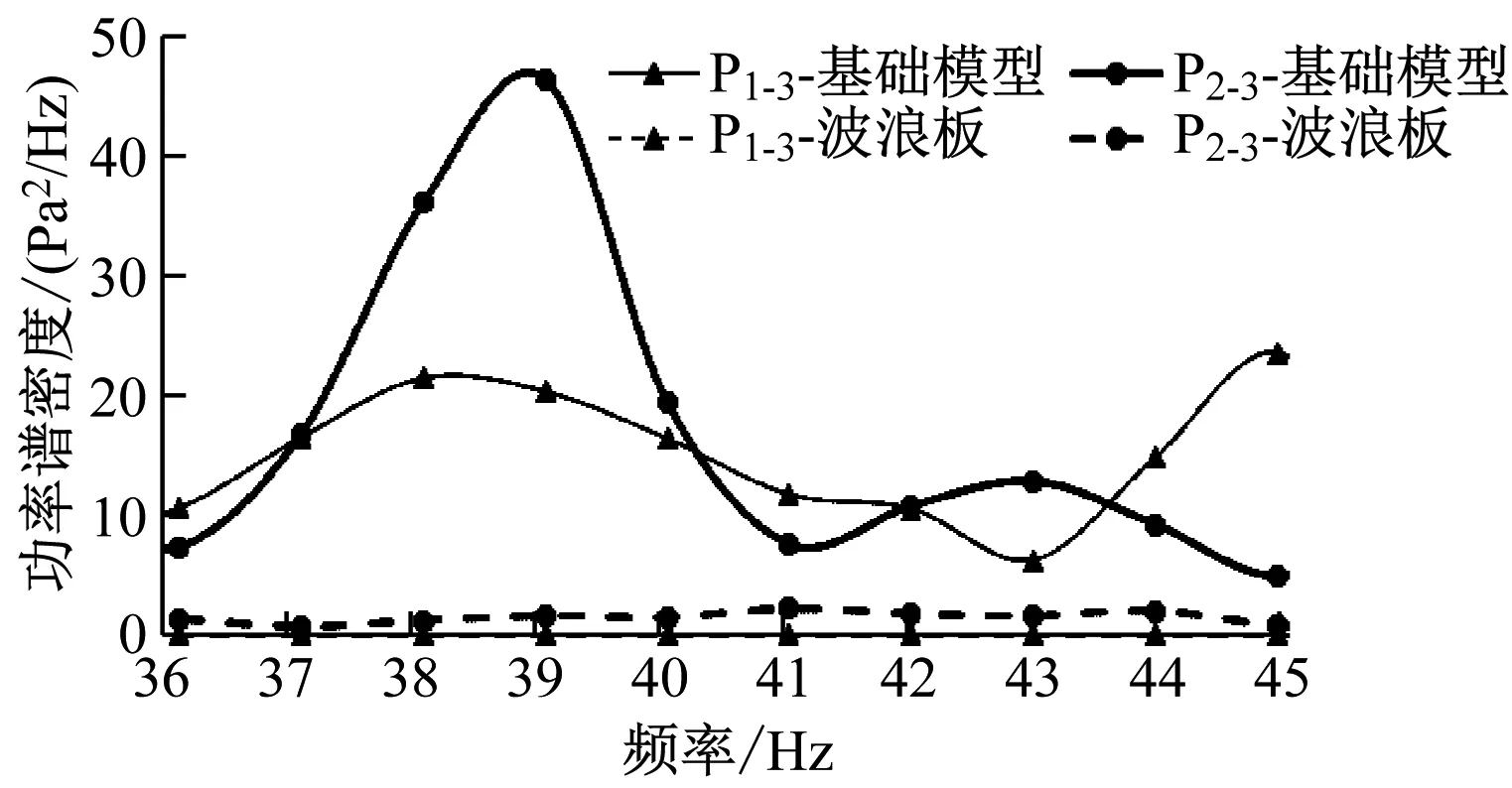
b) 射流方案與基礎模型的對比圖5 波浪板方案、射流方案與基礎模型的 功率譜密度-頻率曲線對比
雖然射流方案降噪效果好,但是在高速列車車廂連接處實施的難度很大。為此,本文僅在線路上測試時進行增加了波浪板控制方案,測試結果如圖6所示。由圖6可知,中心頻率為40 Hz的聲壓級由105.0 dB降低到100.0 dB,降低了5.0 dB。其他頻率的聲壓級也有不同程度的降低,車內總聲壓級由106.5 dB降低到102.5 dB,降低了4.0 dB,可見波浪板控制方案的降噪效果較好。
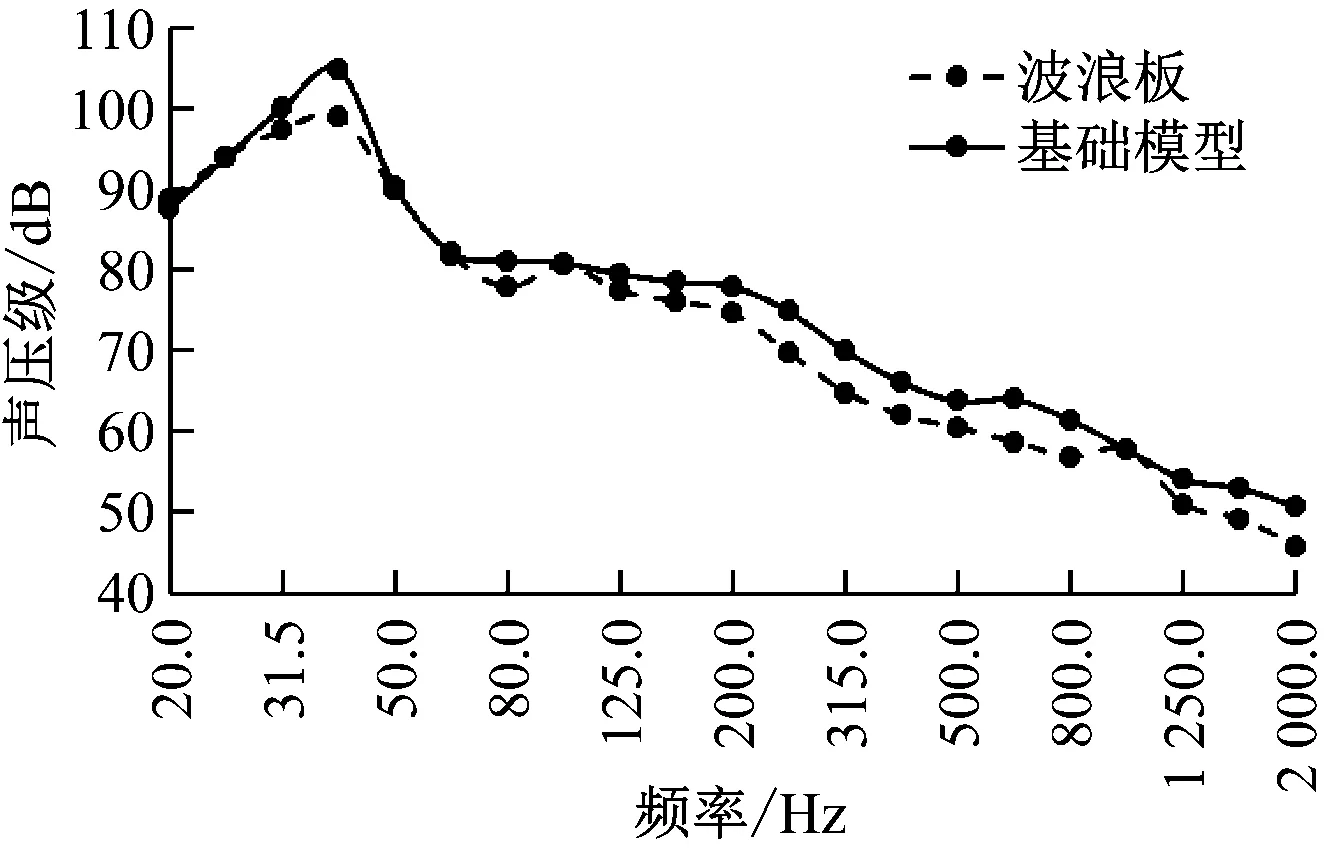
圖6 波浪板方案和基礎模型在不同頻率下的聲壓級對比
3 結語
本文建立了含內、外風擋和端墻的車廂連接處的子域仿真模型,建立了8節編組列車的實車氣動仿真模型,計算得到對應截面的速度、壓力、湍動能和耗散率等參數,以作為子域的邊界條件,采用延遲分離渦模型完成車廂連接處脈動壓力的計算。經計算可知,由上、下缺口射流剪切層頻率和車廂連接處所圍區域的聲腔的二階聲學模態頻率接近,從而產生共振,這是高速列車上車廂連接處附近的乘務員室噪聲過大的主要原因。
為解決此問題,本文提出了基于波浪板的被動流動控制方案,減弱了上、下缺口流動分離,降低了上、下缺口末端脈動壓力和40 Hz所覆蓋帶寬的脈動壓力總能量。實測結果表明:波浪板控制方案能使中心頻率40 Hz的聲壓級降低5 dB,使車內的總聲壓級降低4 dB。
本文進一步提出了基于射流的主動流動控制方案,并對該方案進行了評估。射流方案相當于在缺口部位增加氣幕,以起到屏障和遮擋作用,可顯著減少缺口區域的平均渦量及測點在40 Hz所覆蓋帶寬的脈動壓力總能量。因該方案的實施難度大,本文并未在線路進行實際測試,但根據外部脈動壓力的降低量,可以預測該方案應該能降低車內噪聲,并有望在未來成為可實施的方案。

