港灣式公交中途站停靠承載能力建模分析

潘雷， 李思童， 蘇躍江， 胡郁蔥

(1.廣州市交通運輸研究所， 廣東 廣州 510627；2.華南理工大學 土木與交通學院， 廣東 廣州 510640)

城市常規公交由公交線路和公交站點構成，前者是出行的主要載體，后者是出行的主要受體。載受的不平衡體現在部分公交線路通行能力大于公交中途站停靠承載能力及站點停靠承載能力富余，無法滿足城市人口對公交出行的需求，也導致環境污染、交通擁堵和資源浪費等。目前，港灣式公交中途站設置較廣泛，其通行能力很大程度上影響交通系統，研究港灣式公交站的停靠承載能力對于提升城市公交出行質量具有重要意義。美國《公共交通通行能力和服務質量手冊》和《道路通行能力手冊》在公交停靠站通行能力計算方面取得了豐碩成果。中國也有大量學者對公交站點的停靠能力進行了不同層面的研究，如李凱勝等提出了利用停靠站通行能力計算泊位數的方法；何寧等根據調查所得車輛平均停靠數量、公交車流量和停滯時間等數據建立非線性與線性2種回歸模型，研究公交車站停靠能力的估算方法；呂林考慮乘客需求與車輛供給的匹配情況，分析了公交停靠站的最大承載能力；徐輝等通過分析公交站點停靠承載能力影響因素，建立了公交停靠泊位通行能力模型及多個泊位公交停靠站的泊位利用率值、車輛停靠站通行能力模型。但對港灣式公交中途站停靠能力的研究還不夠完善。該文在美國HCM模型的基礎上進行改進，對港灣式公交中途站停靠承載能力進行研究。

1 模型構建

1.1 公交中途站停靠承載能力影響因素分析

公交中途站停靠承載能力是指在某種特定道路條件下，一個公交車中途站在同一時段內可以滿足停靠的最大車輛數，是公交中途站能為公交車停靠提供的最大供應量。公交車在中途站點停靠的特性如下：

(1) 車輛的到達具有不均勻性。公交車輛的到達服從泊松分布，但受交通信號控制的影響，均勻發車的公交車輛經過一段時間運行后逐漸形成潮汐公交車流，在站點排隊停靠。

(2) 乘客上下車時間具有隨機性。乘客需求量大小影響車輛的服務時間，公交車候車和承載乘客數量較多時，公交車輛在站點的停靠服務時間增大，后續車輛在站點形成排隊等候。

(3) 公交站點設置位置影響其停靠承載能力。公交站點位于道路交叉口附近時，在站點集中排隊停靠，占用站臺長度，車輛在站點的服務時間增大，停靠能力下降。公交中途站遠離交叉口，設置在路段時，社會車流對站點停靠承載能力的影響較小，不易形成排隊停靠現象。

(4) 不同設計形式對公交車輛過站通行時間的影響不同。公交中途站一般有直線式和港灣式2種設計形式。對于直線式停靠站，由于車輛依次排隊按順序進站，后車難以超越前車提前進站，車流進出站點時無法加速，乘客需求量及上下站的時間成為主要影響因素；對于港灣式停靠站，公交車出站時加速匯入其他車道，易與社會車輛產生摩擦，駕駛人會降低車速來避免危險發生，整體進出站時間明顯大于直線式停靠站。當港灣式泊位數>3個時，站點停靠通行能力明顯降低。

(5) 公交車進出站時間受公交站點附近社會車輛車流的影響。當社會車輛在道路上形成密集連續流時，公交車變換車道的時間會受到影響，車輛停靠的延誤時間增加。

該文的研究對象為港灣式公交站。根據以上分析，影響港灣式公交中途站停靠能力的因素可從公交車輛到達、候車及承載乘客數量、道路交通狀態三方面進行分析。在模型計算中，公交車輛到達的影響體現在公交車到達率；候車及乘客數量用乘客上下車時間來體現；道路交通狀態根據不同情況下社會車輛的影響，用延誤等待時間來量化。

1.2 模型假設

(1) 天氣因素對模型的影響忽略不計。

(2) 乘客上下公交車的時間均相同。

(3) 車輛的到達滿足泊松分布，車輛在站點的服務時間滿足愛爾朗分布。

(4) 公交中途站設置在路段上，不考慮交叉口信號燈綠信比及轉彎車流的影響。

(5) 乘客只能在站臺候車上下車，不允許在公交車未進入泊位時上下車。

(6) 乘客下車后，不在港灣式停靠站故意逗留。

(7) 社會車輛不在港灣式站點處停車下客及接客。

(8) 中途站所處路段不考慮設置公交專用道，車輛進站、離站時需變道。

(9) 公交車輛減速進站、加速離站的速度和加速度都相等。

(10) 公交車輛匯入相鄰機動車道時，遵循機動車道社會車輛優先通行的準則。

1.3 模型的建立

以HCM公交通行能力模型為基礎，充分考慮港灣式站點的特殊性及公交車進站和出站的影響。通過排隊論分析計算車輛不同狀態下總消耗時間出現的概率，計算公交停靠消耗的時間。對HCM公交車停靠能力計算方法進行改進，更精確地計算港灣式公交中途站的停靠承載能力。

1.3.1 排隊論模型分析

一般認為所有公交車的到達服從泊松分布，公交車在站點的服務時間服從愛爾朗分布，依照排隊論，公交車輛和中途站形成“單路排隊多通道服務的M/Ek/N”系統：公交站點沒有停靠車輛時，到站的公交車依照到達的前后順序進站停靠，在高峰時段，只要站點有空閑位置，后續形成排隊等待的車輛就進站停靠，遵循“先到先服務”的原則。中途站無車輛停靠的概率為：

(1)

式中：k為排隊車輛數；N為公交車泊位數；ρ為服務強度，ρ=λ/μ；λ為公交車輛總到達率，即單位時間內到達的公交車數量；μ為中途站服務率，即單位時間內一個泊位服務的公交車數量。

中途站有k輛公交車的概率為：

(2)

站點的平均停靠車輛數為：

(3)

車輛在站點的平均排隊長度為：

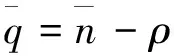
(4)

車輛排隊的平均等待時間為：

(5)

公交車進入中途站停靠的模式分為無需排隊直接進站和按順序排隊進站2種。當載體承載能力小于等于受體承載能力，即公交線路上到達的車輛數小于等于公交站點實際停靠泊位數(k≤N)時，公交車不經過排隊等待，按照順序直接進入公交中途站停靠進行上下客服務；當載體承載能力大于受體承載能力，即公交線路上到達的車輛數大于公交站點實際設置的泊位數(k>N)時，k輛車進入車站完成停靠，N-k輛車在站點外排隊等候，直至前面有車輛完成乘客上下車服務，有空閑車位產生時，排隊車輛依次進入站點停靠。

1.3.2 公交車停靠能力計算方法

HCM通過考慮綠信比、站點滯留時間、消散時間等因素，提出公交車基本停靠能力計算模型，得到單個公交中途站單位小時內能停靠的車輛數。計算公式如下：

(6)

式中：Cb為公交站點的基本停靠能力；g為有效綠燈時間；c為一個周期內綠燈的時長；g/c為有效綠信比，無信號控制時取1；R為折減因子，表征延誤時間變化造成的影響，一般取0.833；D為公交車在站點的滯留時間；tc為公交車在站點的消散時間。

根據式(6)，存在多個泊位的公交中途站的停靠能力為：

(7)

式中：CB為多個泊位的公交站點每小時容納的公交車數量；Neb為多個泊位的有效泊位數。

1.3.3 公交車進出站時間過程

公交車在港灣式中途站停靠的過程可用6段時間進行描述，分別為排隊進入站點時間tw、減速進入站點時間tj、公交車開關車門的時間tm、乘客上下車時間td、加速離開站點的時間tc、匯入機動車道的等待時間th。公交車在港灣式公交站點的總消耗時間T為上述6段時間之和，即：

T=tw+tj+tm+td+tc+th

(8)

乘客上下車的時間和車門開關時間之和即為中途站對車輛的服務時間Tf：

Tf=tm+td

(9)

公交車的服務率為：

(10)

1.3.4 基本停靠能力計算模型修正

(1) 在公交站基本停靠能力計算公式中，候車及承載乘客數量已用乘客上下車占用的時間td量化，即公式中的公交車在站點的滯留時間D。但滯留時間僅包括乘客上下車時間，未考慮公交車減速進站停車的時間和車輛開關門所需時間，需在公式中增加減速進站時間和車輛開關車門時間。設公交車減速進站的速度為v1，減速進站的加速度為aj，則公交車減速進站的時間tj可按式(11)計算。設公交車加速出站的速度為v2，加速出站的加速度為ac，則車輛加速離站的時間tc可按式(12)計算。

(11)

(12)

p3=P(h≥τ)=e-Qτ/3 600

(13)

p4=P(h<τ)=1-e-Qτ/3 600

(14)

(15)

(16)

(3) 公交車進站分為直接進站和排隊等待進站2種情況，需考慮車輛進站的排隊時間。根據排隊論，公交車在站點外排隊等待的平均時間按式(17)計算。k≤N時，車輛直接進站，根據式(2)，直接進站的公交車輛概率按式(18)計算。式(1)、式(2)聯合得到式(19)。根據上述對公交車進出站時間的分析，公交車的進出站可劃分為直接進站、直接出站，直接進站、排隊出站，排隊進站、直接出站和排隊進站、排隊出站4種情況，其總消耗時間分別按式(20)～(23)計算。在不考慮信號燈綠信比的前提下，港灣式多泊位站點實際通行能力按式(24)計算。

(17)

(18)

p2=1-P(0)-p1

(19)

T1=tj+tm+td+tc

(20)

T2=tj+tm+td+tc+th

(21)

T3=tw+tj+tm+td+tc

(22)

T4=tw+tj+tm+td+tc+th

(23)

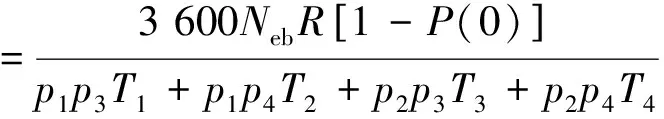
(24)

式中：T1為直接進站、直接出站的公交車在站點的總消耗時間；T2為直接進站、排隊出站的公交車在站點的總消耗時間；T3為排隊進站、直接出站的公交車在站點的總消耗時間；T4為排隊進站、排隊出站的公交車在站點的總消耗時間；p1為直接進站的公交車出現的概率；p2為排隊進站的公交車出現的概率；p3為直接出站的公交車出現的概率；p4為排隊出站的公交車出現的概率。

2 實證研究

廣州市馬場路為雙向六車道，設計速度為 60 km/h，高峰期單向交通量約為 3 000 pcu/h。馬場路公交中途站設置在道路最南側，為港灣式中途站，車站停靠泊位數為2個，即Neb=2個(見圖1)。道路交通狀況見表1。

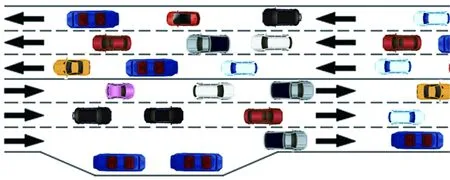
圖1 公交站道路運行情況

表1 站點交通運行狀況

經調查，共有5條公交線路途經馬場路公交中途站，分別為138 路、407 路環線、499 路、545 路、901A 路公交線路，線路發車間隔見表2。

表2 站點途經公交線路發車間隔

根據實際調查和相關經驗，取tm=3.5 s，td=2.5 s，v=35 km/h，aj=1.5 m/s2，ac=1 m/s2，則進站時間tj=v/aj=6.5 s，出站時間tc=v/ac=9.7 s。

將tm、td代入式(9)、式(10)，得Tf=28.5 s、μ=0.035 pcu/s。由表2得λ=0.018 9 輛/s、ρ=λ/μ=0.54。

將Neb、ρ代入式(1)、式(17)～(19)得：P(0)=57.48%、tw=2.27 s、p1=39.42%、p2=3.10%。

以高峰期單向交通量為基礎，求得單車道交通流Q=1 000 pcu/h。將機動車道上所有車輛視作小汽車(小型車)，單車道寬取7.8 m，參考HCM模型，取τ=6 s。將Q、τ代入式(13)、式(14)、式(16)，得p3=0.189、p4=0.811、th=9.46 s。

將tw、tj、tm、td、tc、th分別代入式(20)～(23)，得T1=44.7 s、T2=54.16 s、T3=46.97 s、T4=56.43 s。

將上述計算結果代入式(24)，得馬場路公交站點在高峰期的通行能力C總=113輛/h。取D=tm+td=28.5 s，根據高峰期車輛調查結果，取清空時間tc=15 s，代入式(7)，得CB=138 輛/h。

調查結果顯示，1 h內馬場路公交站所服務的車輛為142輛。修正前模型計算所得服務車輛數為124輛/h，其偏差為12.7%，而修正后模型的偏差僅為2.8%，其計算結果更貼近實際調查情況。

3 結論

(1) 公交中途站的承載能力受道路運行情況、路段飽和度及途徑公交線路到站概率等因素的影響。

(2) 港灣式公交中途站經停線路的車輛到達存在4種類型，公交車輛到站情況不同，則其到達概率不同，直接影響中途站的承載能力。

(3) 經案例驗算，修正后中途站承載能力模型與實際道路運行情況較契合，可為合理布設公交站點泊位和規劃公交線路公交車數量提供參考。