基于量綱分析的彈塑性應力強度因子探討
張 錚,李澤商,王依兵
(北京航空航天大學航空科學與工程學院, 北京 100191)
0 引言
斷裂失效是航天系統結構的主要失效模式,零部件的斷裂失效給航天結構的安全運行帶來極大威脅。實際航天工程結構(材料)中總是不可避免地存在著各種不同形式的缺陷(如孔洞、裂紋),孔洞、裂紋、應力集中等問題是引起航天構件失效的主要原因之一,斷裂力學是研究裂紋問題的主要固體力學分支學科。自20世紀40年代末產生以來,斷裂力學經過半個多世紀的發展,取得了豐碩的研究成果。
斷裂力學包含線彈性斷裂和彈塑性斷裂兩大類問題。其中,線彈性斷裂力學適用于強度較高的脆性材料的斷裂行為,而彈塑性斷裂力學適用于裂紋尖端存在較大塑性區的情況。
在線彈性斷裂力學中,具有重要的地位和作用的力學參量是表征裂紋尖端場強度的應力強度因子。1957年,Irwin首次提出了應力強度因子的概念,當應力強度因子達到材料斷裂韌度時材料發生新的裂紋擴展。彈塑性斷裂力學認為裂紋尖端應力場進入塑性,表征線彈性的應力強度因子不再適合表征彈塑性裂紋尖端應力場,而采用J-積分作為彈塑性裂尖場強度的表征量。
張行、洪起超的研究表明,J-積分既適用于表征彈塑性場,又適用于線彈性場;而應力強度因子只適用于線彈性場。然而,相對于應力強度因子簡明清晰的物理含義,J-積分的定義式顯得相對繁復隱晦,缺乏明確的物理意義。上述問題不僅使得對裂紋尖端場的物理認識存在困難,在應用上也造成材料的彈/塑性斷裂判據缺乏一致性。
本文以Ⅲ型裂紋(反平面剪切)問題為例,依據斷裂力學已經建立的彈/塑性裂尖場(包括應力強度因子和J-積分),引入材料彈塑性本構關系,通過理論推導和與現有裂尖場解的對比分析,建立了如線彈性裂尖場應力強度因子形式的彈塑性應力強度因子,用以表征彈塑性裂尖場強度,進而建立可同時適用于材料線彈性和彈塑性斷裂的一般性判據。
1 Ⅲ型裂紋問題的彈塑性分析
1.1 基本假設
對于圖1所示的典型Ⅲ型裂紋模型,假設截面上任意一點只有垂直截面的位移,即
=(,)
(1)
式中,(,)表示無限長棱柱任意截面內(,)處的位移。
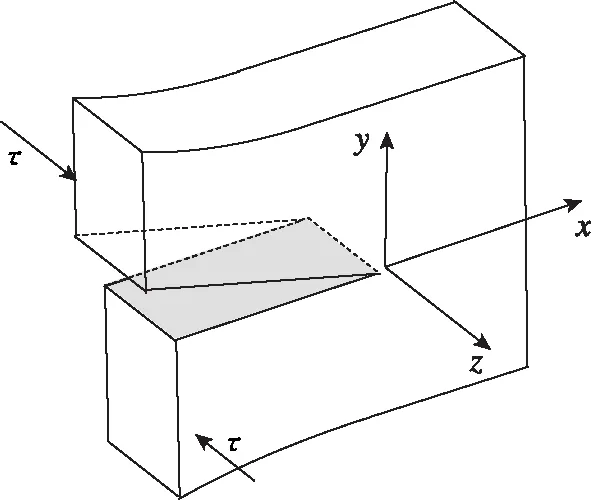
圖1 Ⅲ型裂紋的空間和平面圖示Fig.1 Spatial representation of model-Ⅲ crack
1.2 平衡方程[16]
平衡方程為
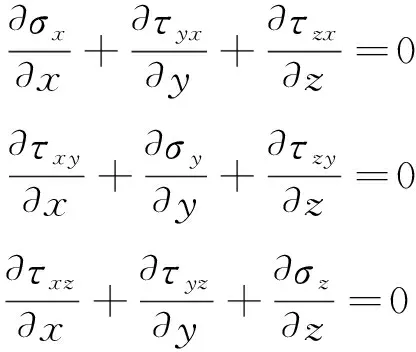
(2)
式中,表示方向的正應力,表示方向平面的方向切應力。
1.3 幾何方程
需要說明的是,雖然考慮裂紋尖端場應力進入塑性,但由于裂尖場是大集度場,其區域遠小于宏觀尺度,材料變形處于小范圍塑性狀態,因此不失一般性,這里仍然采用線性幾何關系,即
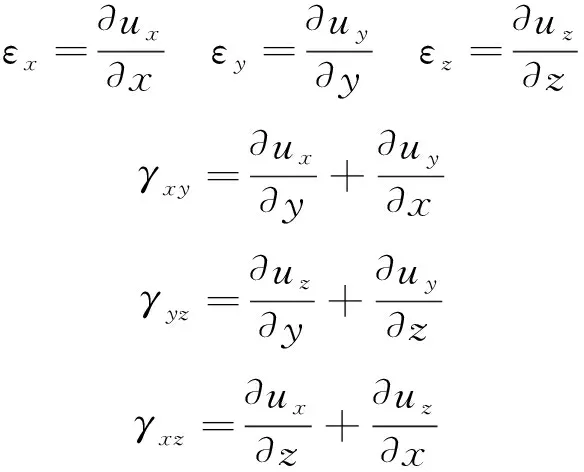
(3)
式中,表示方向正應變,表示切應變。
將式(1)代入上式,有
=====0


(4)
1.4 本構關系
如式(5)所示,Ramberg-Osgood方程是表示材料彈塑性本構關系的一般性表達式。
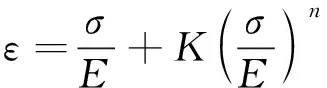
(5)
式中,為楊氏模量,為拉伸應變硬化指數,為硬化系數。
本文所討論的裂尖場(如“1.3 幾何方程”中所述),雖然是“小范圍塑性”場,但在裂尖影響區內,塑性變形是主導性的,即彈性變形遠小于塑性變形。因此,可將Ramberg-Osgood方程簡化為
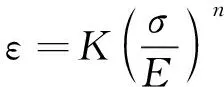
(6)
相似地,有剪切本構方程

(7)
式中,為剪切硬化系數,為剪切模量。
按照式(6)(7)的形式,Ⅲ型斷裂問題的彈塑性本構關系可表達為

(8)
式中,表示泊松比。
將幾何關系式(4)代入彈塑性本構關系式(8),有
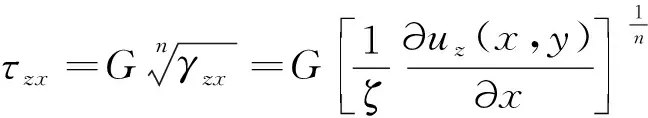
(9)
再將式(9)代入平衡方程式(2),有
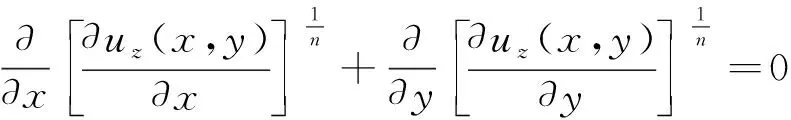
(10)
式(10)結合邊界條件即可求得問題解。
2 彈塑性Ⅲ型裂紋問題求解
通過上述推導可知,本問題的控制方程,即式(10),為二階非線性橢圓型偏微分方程,斷裂力學中常規的復變函數解法難以適用,也缺乏其他簡明的求解方法。因此,本文參照現有的斷裂力學解,采用半逆解法進一步分析裂尖彈塑性場,從而解析出彈塑性裂尖場的應力場分布。
參看式(1),并參照線彈性斷裂力學分Ⅲ型裂紋分離變量形式的解,假設Ⅲ型裂紋的彈塑性應力場分布函數為
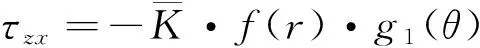
(11)
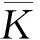
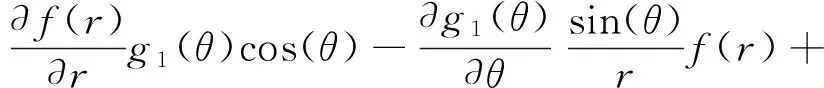
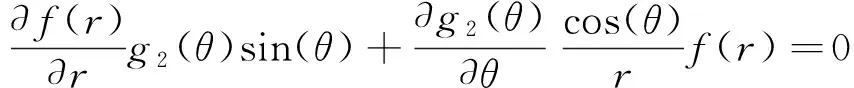
(12)
觀察式(12)的形式,參照線彈性場的分布函數,可以發現
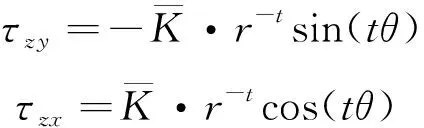
(13)
可以滿足該式。進一步,考察應力表示的相容方程

(14)
式中,=++為應力不變量,將應力場函數式(13)代入上述相容方程式(14),即可證明后者成立。
3 彈塑性應力強度因子的定義
一般斷裂力學教科書中,定義線彈性裂尖場的應力強度因子為

(15)
式中,為載荷對應的遠場應力,表示裂紋半長。
對于彈塑性裂尖場而言,通常都是采用J-積分來表征
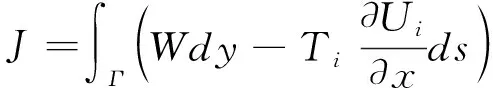
(16)
式中,為從裂紋下表面沿著逆時針方向轉到裂紋上表面,包圍裂紋尖端的任意積分路徑,為外力分量,為位移分量,為積分路徑上的線元,為應變能密度。
可見其表達式比較繁復隱晦。相比于線彈性場的特征量即應力強度因子,影響彈塑性裂尖場的因素不是顯式的,其作用規律也不是顯式的函數形式。
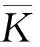
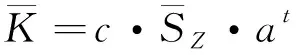
(17)
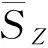

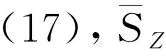
根據彈塑性斷裂力學分析,裂尖應力場可表示為
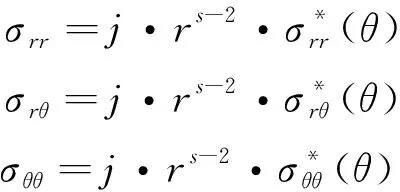
(18)
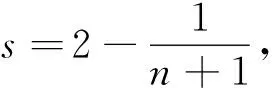

(19)
綜上所述,類比于線彈性裂尖場的應力強度因子,式(17)定義了彈塑性裂尖場的彈塑性應力強度因子,二者的對比如表1所示。

表1 線彈性應力強度因子與彈塑性應力強度因子
4 彈塑性應力強度因子的合理性
首先,對于線彈性裂尖場,應力強度因子是表征應力場強弱的力學參量。當載荷造成裂紋擴展時,應力強度因子的臨界值可視作材料的斷裂強度,即材料斷裂韌度。
其次,本文依托彈塑性裂尖場定義了相應的彈塑性應力強度因子,該參量同樣表征裂尖應力場的烈度/集度;當載荷造成裂紋擴展時,彈塑性應力強度因子可以替代J-積分,其臨界值同樣可以視作材料斷裂韌度,也就是說,可以根據本文定義的彈塑性應力強度因子建立材料斷裂的新判據,而彈塑性應力強度因子的含義遠比J-積分要簡明。這是本文研究的重點。
由此,建立與彈塑性應力強度因子相應的實驗方法和相應斷裂韌度的測量方法,不僅具有簡明的理論基礎,也將有助于簡化實驗,方便應用。這也是本文研究的意義。
需要指出的是,本文方式同樣適用于定義Ⅰ型和Ⅱ型裂紋的彈塑性應力強度因子,表征其彈塑性裂尖場的集度。
5 結論
綜上所述,本文首先基于斷裂力學基本概念和理論,對基于Ⅲ型裂紋(反平面剪切問題)進行分析,在彈塑性場中建立了該問題的幾何方程、本構方程和平衡方程。
然后參照線彈性場中裂紋尖端應力分布函數,建立了彈塑性場中的裂紋尖端應力分布函數,并基于理論推導,在裂紋尖端應力分布函數、強度因子、的指數和角分布函數4方面對比彈塑性場與線彈性場,定義了類比于線彈性場中應力強度因子的參數,即彈塑性應力強度因子,來表征彈塑性裂紋尖端應力場強度。
本文對提出的彈塑性應力強度因子在表達形式、物理意義、量綱和普適性等方面分別進行分析,闡述了彈塑性應力強度因子涵蓋彈塑性裂紋尖端場的表征意義,明確了其概念的內涵、定義和合理性基礎,因而確立了該參量對彈塑性裂紋尖端場固有特質的表征。由此也說明,根據彈塑性應力強度因子可以建立適用于材料彈性/彈塑性斷裂的一般性判據。

