不同維分數階混沌預設時間有限時間投影同步

邵克勇 蔣盧杰 王婷婷

摘?要：對于不同維分數階混沌系統的投影同步問題，設計了一種自適應滑模控制器。這使得帶有內部不確定量和外部擾動的驅動，響應系統能夠在任意預設的時間完成同步，自適應律可以逼近未知量的上界。?并針對自適應滑模控制器由于干擾產生抖振的問題，提出了兩種解決方案。首先是設計二維滑模控制表，將模糊控制方法加入滑模控制器組成模糊自適應滑模控制器。其次是使用“SuperTwisting”控制律，將滑模控制改進為二階滑模控制。最后通過數值仿真，可以看到兩種解決方案都有效地削減了控制器的抖振現象，證明了方法有效性和正確性，提高了用于實際生產的可行性。

關鍵詞：模糊自適應滑模控制;二階滑模控制;有限時間同步;分數階混沌系統;SuperTwisting算法

中圖分類號：TP?273???????文獻標識碼：A

Finitetime?Projection?Synchronization?of?Different

Dimensionality?Fractional?Chaos?at?the?Preset?Time

SHAO?Keyong，?JIANG?Lujie，?WANG?Tingting

（School?of?Electrical?Engineering?&?Information，?Northeast?petroleum?University，?Daqing?，Helongjiang?163318，?China）

Abstract：For?the?projective?synchronization?of?fractionalorder?chaotic?systems?with?different?dimensions，?an?adaptive?sliding?mode?controller?is?designed.?The?drive?and?response?system?with?internal?uncertainty?and?external?disturbance?can?be?synchronized?at?any?preset?time，?and?the?adaptive?law?can?approach?the?upper?bound?of?the?unknown.?Two?solutions?are?proposed?for?the?chattering?problem?of?adaptive?sliding?mode?controller?due?to?interference.?The?first?is?to?design?a?twodimensional?sliding?mode?control?table，?and?add?the?fuzzy?control?method?to?the?sliding?mode?controller?to?form?a?fuzzy?adaptive?sliding?mode?controller.?The?second?is?to?use?the?"SuperTwisting"?control?law?to?improve?sliding?mode?control?to?secondorder?sliding?mode?control.Finally，?through?numerical?simulation，?it?can?be?seen?that?the?two?solutions?have?effectively?reduced?the?chattering?phenomenon?of?the?controller，?proved?the?effectiveness?and?correctness?of?the?method，?and?improved?the?feasibility?of?being?used?in?actual?production.

Key?words：fuzzy?adaptive?sliding?mode?control;?secondorder?sliding?mode?control;finite?time?synchronization;?fractionalorder?chaotic?system;?SuperTwisting?algorithm

混沌現象是對于初值十分敏感的復雜非線性現象，經常出現于自然或人工的系統中。分數階混沌由于擁有分數階運算和高度的非線性，呈現出比整數階混沌更復雜的行為。這個特性對于工程應用十分重要，如降低安全通信中被攻擊的風險[1]。近些年，對于分數階混沌同步的研究受到了廣泛關注，關于分數階混沌系統間的各種同步方式及方法被提出[2-8]，但基于不同維分數階混沌系統的有限時間投影同步的研究還相對較少。結合以上的考慮，本文設計分數階自適應滑模投影同步的控制方法，在保證了系統魯棒性穩定的前提下，還能對未知可變的內外因素進行適應，使得系統間的同步時間僅僅依賴于初始條件及參數，無須考慮未知量的上界。

1?預備知識

引理4[12]?如果一個受控系統有如下形式：

式中x∈R是狀態變量，φt是干擾量，ut為“SuperTwisting”控制律

其中u1（t）=-λ|x|12sgn（x），2=-αsgn?（x），α>0，λ>0為參數，sgn?（x）為符號函數。若|t|≤δ，t≥0，δ為已知常數，設定參數

則系統可以在有限時間收斂到原點。

2?不同維分數階系統預設時間的有限時間投影同步

2.1?問題描述

考慮不同維的分數階驅動系統與響應系統，它們的形式分別如下：

其中α∈0，1是分數階微分的階次，Dα既可以是Caputo型也開始是RL型微分，Y=y1，…，ym∈Rm和X=x1，…，xn∈Rn分別為響應系統與驅動系統的狀態變量，gi：Rn→R，i=1，2，…，n是X的非線性函數，Δg（X，t）=[Δg1（X，t），…，Δgn（X，t）]和dg（t）=[dg1（t），…，dgn（t）]分別是驅動系統的內部不確定量和外部擾動，fi：Rn→R是Y非線性函數，?Δf（Y，t）=[Δf1（Y，t），…，Δfm（Y，t）]和df（t）=[df1（t），…，dfm（t）]分別是響應系統的內部不確定量和外部擾動。最后u（X，Y，t）=[u1（X，Y，t），…，um（X，Y，t）]為控制信號。假設外部干擾和內部不確定性是有界可微的。

系統間的誤差表達式可以寫作Ε（t）=Y（t）-A·X（t），Ε（t）=[e1，…，em]∈Rm，其中A=[a1，…，ai，…，am]∈Rm×n為兩個系統間投影同步的系數矩陣，ai為行向量。將式（1）和式（2）代入誤差公式，系統間誤差的分數階微分方程可以表示為：

2.2?控制器設計

采用以下滑模面：

其中hit被稱作終端函數，假設在控制器的作用下驅動系統和響應系統在時間t=T時達到同步，T為預先設置的時間參數。則終端函數hit應當滿足在時刻T時hi（T）=0，而在初始條件下hi（0）=ei0。于是選擇如下形式終端函數hit：

定理1?對于驅動系統（1）和響應系統（2），在其內部不確定量與外部擾動是未知的情況下，設計公（7）形式的自適應控制器，實現兩個系統在時刻T的同步。

證明：將終端函數hit式（5）代入滑模面的表達式（4）中，可以得出t=0時，si（0）=ei（0）-ei（0）=0，即系統一開始便位于滑模面上。滑模面的特性使得誤差ei（t），=hit誤差函數的軌跡將會按照終端函數的軌跡運行，而在時間t=T時，ei（T）=hiT=0系統達到同步。可以看到系統同步的時間取決于終端函數中參數T的選擇。這種終端滑模面的設計方法省略了到達階段，增強了系統的魯棒性和精確性。但當出現內部不確定與外部擾動時，系統會偏離滑模面，為了保證系統能在這種條件下返回滑模面，需要對其收斂性進行分析。

當系統的內部不確定與外部擾動上界已知時，設計的lyapunov函數為：

而對于未知的上界，需要引入自適應律，因此將式（8）?改進為

其中i=i=θi，式（9）只有在零點時為0，而其他情況下大于0。由此可以得出該lyapunov函數為正定，對式（9）求導可得

進一步地將式（4）代入式（10）展開，根據引理1可得

根據引理2，在展開后的式子中，分數階積分算子和分數階微分算子進行運算可得：

由于擾動都是有界且可導的，根據Hlder空間特性[13]可知，Fui，Gui，DMi，DSi滿足之前提出的不等式，因此：

其中kmin?=min?（k1，k2，…，km），當si=0時t，i=0，導函數為負定。上述不等式證明了誤差系統漸近穩定于滑模面，即相軌跡因為擾動離開滑模面時，能夠在控制器的作用下回到穩定狀態。通過引理3式（13）可以變為

根據有限時間穩定性判據[14]，由以上微分不等式可以推導出系統會在有限時間內返回滑模面，其時間上的界取決于參數kmin?。

系統回到滑模面上后，s（t）=0，根據式（4），系統誤差與終端函數的關系變為0=ei（t）-hit，誤差將會在時間t=T時變為0，從而達到同步。由此可知，只要設計合適的趨近律參數，使得系統返回滑模面的時間遠小于同步時間T，那么系統就能在發生微小偏移時迅速回歸滑模面，實現在預設時間T達到同步，證明完畢。

2.3?控制器的改進

傳統滑模控制的一個缺點便是當滑模面上出現干擾時，控制器會出現劇烈的抖振，這在實際使用滑模控制器的過程中帶來了巨大的挑戰，抖振不但會給設備帶來損害，還會影響系統的表現。模糊控制是基于專家經驗所指定的語言規則的集合，運用這些規則集合可以提供適當的模糊控制律，將模糊控制運用到滑模控制，就是所謂的模糊滑模控制[10]。

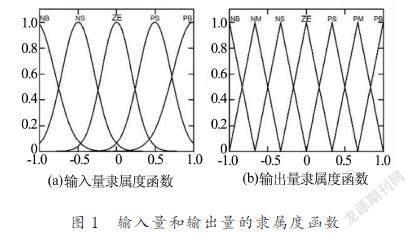
加入模糊控制后，原本控制器中的（ui+|ai·u|+|ai·M|+Si）·sgn?si變為（ui+|ai·u|+|ai·M|+Si）·sfi，sfi是經過模糊推理后得出的輸出量。模糊控制表可以由專家經驗或實驗得出，為了使得控制器的輸出更加適當，調模糊控制選擇兩個輸入量，這樣可以從輸入量中獲得更多的信息從而防止控制器輸出過大出現超調，進而減小或消除控制器中的抖振，選擇的兩個輸入量是滑模面與滑模面的導數。圖1為輸入量與輸出量的隸屬度函數。輸入量根據數據統計的直方圖與呈現出的正態分布曲線選擇了高斯函數。輸出量需要精確數值，因此選擇了三角形函數。

將輸出量劃分為七個范圍，分別是負大（negative?big，NB）、負中（negative?middle，NM）、負小（negative?small，NS）、零（zero，ZE）、正小（positive?small）、正中（positive?middle，PM）、正大（positive?big，PB），而兩個輸入量被劃分為五個范圍，?分別是NB、NS、ZE、PS、PB。?表1為模糊自適應滑模控制規則表。

模糊控制的引入雖然可以減小抖振的影響，但作為額外的結構，給控制器的設計增添了復雜度。接下來結合二階滑模理論中的SuperTwisting算法，對控制器進行改進。

定理?2?對于驅動系統（1）和驅動系統（2），其內部不確定量與外部擾動是未知的，Dα?選為Caputo型，設計如下的自適應控制器，實現兩個系統在時刻T的同步

證明：與定理1采用相同的終端函數，系統在初始時間便位于滑模面上，因此為了保證系統能在預設時間達到同步，需要系統在偏離滑模面后在有限時間內返回。將控制器（15）帶入滑模面動態系統公式（4）展開并求導，可以得到

根據2.2節中對內部不確定和外部擾動的假設，將Δfi（Y，t）-ai·Δg（X，t）+dfi（t）-ai·dg（t）記為φ（X，Y，t），則|（X，Y，t）|≤δ，δ屬于已知常數，所以可得

根據引理4，受控系統si在有限時間內達到穩定點，此時系統達到滑模面，即s（t）=0。系統到達滑模面后，系統的誤差就會跟隨終端函數hit的軌跡，在時間t=T時達到同步。而趨近律保證了系統偏離滑模面時能夠在有限時間內回到滑模面。由此可知，保證在預設時間達到同步的前提是返回滑模面的時間足夠短，而返回時間的長短可以由參數來設定，證明完畢。

針對分數階混沌系統的投影同步問題，通過帶有分數階積分項形式的滑模控制器，將整數階領域的二階滑模控制方法應用于分數階系統上，對整數階二階滑模控制的應用進行了擴展。

3?數值仿真

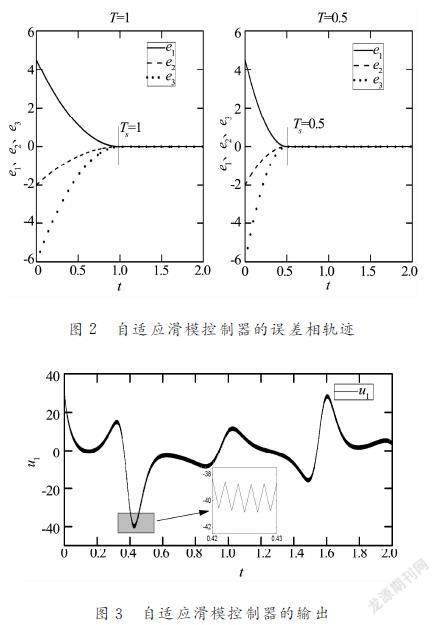
選擇擁有內部未知量與外部擾動的四維分數階超混沌系統和三維分數階chen混沌系統作為驅動系統和響應系統。首先使用自適應滑模控制器，設置同步時間T?分別為0.5和1，各個維度的誤差相軌跡如圖2所示，系統的在設定的時間點誤差收斂到零達到了同步，證明了控制器的有效性。

圖3為時間參數T=1時自適應滑模控制器的輸出，可以看出有明顯的抖振，為了解決這個問題，緊接著分別采用了模糊自適應滑模控制器與二階滑模控制器，對驅動和響應系統進行同步實驗，時間設置為T=1，圖4為使用兩種改進后的控制器的誤差相軌跡圖，可以看到在規定時間達到同步。

圖5和圖6顯示了控制器u1的輸出，可以看到在保證了在有限時間同步的同時，運用模糊控制與SuperTwisting控制律的滑模控制器輸出曲線光滑連續，使得滑模控制器有效地消除了因為外界擾動帶來的抖振。表2在中展現了三種控制器的各項性能，可以看到與自適應滑模控制器相比，模糊自適應滑模控制器在平均收斂時間、最大輸出和平均輸出三項上的表現更優，而穩態最大誤差的表現略差;二階滑模控制器的各項性能均優于普通的自適應滑模控制器;對比兩種改進的控制方法，自適應滑模控制器在最大輸出的性能上更具優勢，二階滑模控制器的穩態最大誤差和平均輸出的性能則高于滑模自適應滑模控制器，而平均收斂時間的表現兩者相同。

4?結?論

結合分數階微積分性質、自適應控制與有限時間穩定性分析、滑模控制器等知識，成功設計了不同維分數階混沌系統間的同步控制器，可以在預設時間到達有限時間投影同步。控制器中的自適應律能夠逼近內部不確定性和外部擾動范圍的上界，使得同步時間不再依賴對干擾的估計。同時針對滑模控制器容易產生抖振的情況，從增加控制結構和改善滑模控制自身兩方面入手：首先，根據實際情況統計數據、選擇隸屬度函數、設計二維模糊控制規則，將設計好的模糊控制與自適應滑模控制結合，提出了模糊自適應滑模控制，可以根據具體系統的表現設計模糊規則;其次，以自適應滑模控制器為基礎，將整數階的SuperTwisting控制律運用到分數階系統上，使控制器擴展為分數階系統的二階滑模控制，由于沒有增加額外結構使得控制器的實現更加簡單。兩種方法無論是從抖振幅度還是抖振頻率都對滑模控制進行了削減，并通過仿真對各自性能的優劣進行了分析。

參考文獻

[1]?KIANIB?A，?FALLAHI?K，?PARIZ?N，?et?al.?A?chaotic?secure?communication?scheme?using?fractional?chaotic?systems?based?on?an?extended?fractional?Kalman?filter?[J].?Communications?in?Nonlinear?Science?and?Numerical?Simulation，?2009，?14（3）：?863-879.

[2]?KHANZADEH?A，?POURGHOLI?M.?A?novel?continuous?timevarying?sliding?mode?controller?for?robustly?synchronizing?nonidentical?fractionalorder?chaotic?systems?precisely?at?any?arbitrary?prespecified?time?[J].?Nonlinear?Dynamics，?2016，?86（1）：?543-58.

[3]?SHIRKAVAND?M，?POURGHOLI?M.?Robust?fixedtime?synchronization?of?fractional?order?chaotic?using?free?chattering?nonsingular?adaptive?fractional?sliding?mode?controller?design?[J].?Chaos，?Solitons?&?Fractals，?2018，?113：135-47.

[4]?MOFID?O，?MOBAYEN?S.?Adaptive?synchronization?of?fractionalorder?quadratic?chaotic?flows?with?nonhyperbolic?equilibrium?[J].?Journal?of?Vibration?and?Control，?2018，?24（21）：?4971-4987.

[5]?MOHAMMADZADEH?A，?GHAEMI?S.?A?modified?sliding?mode?approach?for?synchronization?of?fractionalorder?chaotic/hyperchaotic?systems?by?using?new?selfstructuring?hierarchical?type2?fuzzy?neural?network?[J].?Neurocomputing，?2016，?191：200-213.

[6]?GAO?Like，WANG?Zhihui，ZHU?Wenji，?et?al.?Modified?sliding?mode?synchronization?of?typical?threedimensional?fractionalorder?chaotic?systems?[J].?Neurocomputing，?2015，?166：53-58.

[7]?ZHANG?Xingpeng，?ZHANG?Xiaohong，?LI?Dong，?et?al.?Adaptive?synchronization?for?a?class?of?fractional?order?timedelay?uncertain?chaotic?systems?via?fuzzy?fractional?order?neural?network?[J].?International?Journal?of?Control，?Automation?and?Systems，?2019，?17（5）：?1209-1220.

[8]?BEHINFARAZ?R，?BADAMCHIZADEH?M?A，?GHIASI?A?R.?An?approach?to?achieve?modified?projective?synchronization?between?different?types?of?fractionalorder?chaotic?systems?with?timevarying?delays?[J].?Chaos，?Solitons?&?Fractals，?2015，?78：95-106.

[9]?AGHABABA?M?P，?KHANMOHAMMADI?S，?ALIZADEH?G.?Finitetime?synchronization?of?two?different?chaotic?systems?with?unknown?parameters?via?sliding?mode?technique?[J].?Applied?Mathematical?Modelling，?2011，?35（6）：?3080-3091.

[10]LI?Chenkuan，?LI?Changpin.?Remarks?on?fractional?derivatives?of?distributions?[J].?Tbilisi?Mathematical?Journal，?2017，?10（1）：?1-18.

[11]POLYA?G，?HARDY?G?H，?LITTLEWOOD.?Inequalities?[M].Cambridge：Cambridge?University?Press，?1952.

[12]李鵬，?鄭志強.?基于類二次型?Lyapunov?函數的?Supertwisting?算法收斂性分析?[J].?控制與決策，?2011，?26（6）：?949-952.

[13]MUOZVZQUEZ?A?J，?PARRAVEGA?V，?SNCHEZORTA?A?.?Uniformly?continuous?differintegral?sliding?mode?control?of?nonlinear?systems?subject?to?Hlder?disturbances?[J].?Automatica，?2016，?66：179-184.

[14]TANG?Yu.?Terminal?sliding?mode?control?for?rigid?robots?[J].Automatica，?1998，?34（1）：?51-56.