挖“教材”之本 體“源題”之活*
——從一道幾何證明題談起
?江蘇省南通市海門區海南中學 朱愛平
1 引言
本文中以人教版八年級下冊第十八章“平行四邊形”第69頁的第14題為例,分析如何挖掘教科書上的習題,通過設置階梯問題引導學生進行深度思考分析,利用圖形變式提升學生遷移能力.通過一題多變、一題多解,有意識地引導學生從“變”的現象中發現“不變”的本質,從不變的本質中探究“變”的規律,培養學生的探索精神和創新意識,提高學生數學核心素養,給予學生帶得走的知識.
2 原題呈現
如圖1,四邊形ABCD是正方形,點E是邊BC的中點,∠AEF=90°,且EF交正方形外角的角平分線CF于點F,證明:AE=EF.(提示:取AB中點G,連接EG.)
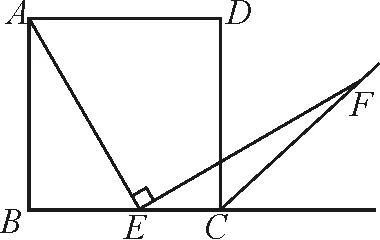
圖1
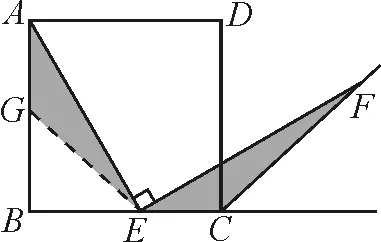
圖2
3 分析引導
思路分析:從結論需要證明AE=EF出發,聯想到可證明全等,觀察圖形需要構造全等,由條件點E是BC的中點聯想取AB的中點G.如圖2,證明△AGE≌△ECF.根據練習后面給予的提示,學生能夠自行解決此問題.但如果僅僅停留在表層問題的解決,那真是入寶山而空手回了.
引導1:點E是BC的中點這個條件是否可以修改呢?
學生容易想到:點E為BC上任意一點.
引導2:如果點E為BC上任意一點,其余條件不變,如圖3,那么AE=EF還成立嗎?
引導3:動手畫一畫,探究一下.此時在構造全等時,還是取AB的中點G嗎?你是怎么取的?為什么這樣取呢?
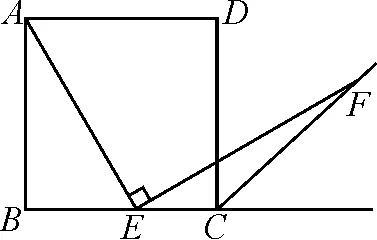
圖3
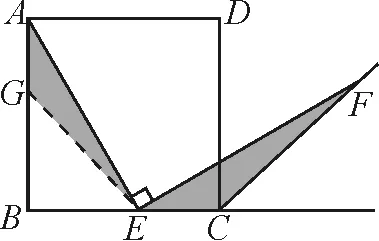
圖4
這樣的變式問題,學生能夠遷移方法,還是會去構造△AGE≌△ECF(如圖4),則需要AG=EC.所以在AB上截取AG=EC,連接EG,在證明∠AGE=∠ECF=135°時,需要根據等式性質證明BG=BE,所以在作輔助線時,也可以在AB上截取BG=BE,再去證明.
設計意圖:通過畫圖簡單的變化,鍛煉學生的畫圖能力,這個過程每個學生都能夠嘗試,在學生嘗試畫圖的過程中發現自己又能夠嘗試去解決問題,從而增加學生嘗試探究的信心.在學生最近發展區設置問題,遵循了學生的認知規律,增強了學習數學的信心,給足學生探究的時間,慢慢使學生敢于創新.
引導4:你還能對點E的位置做怎樣的改變?請把它畫出來,此時AE=EF還成立嗎?畫一畫,觀察嘗試一下.
學生會將點E的位置聯想到BC的延長線上或CB的延長線上,如圖5、圖6.
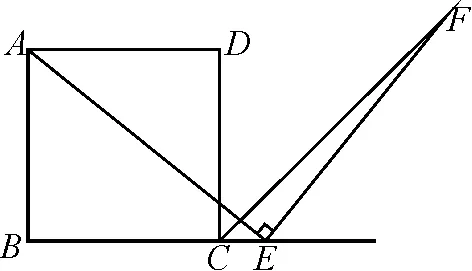
圖5
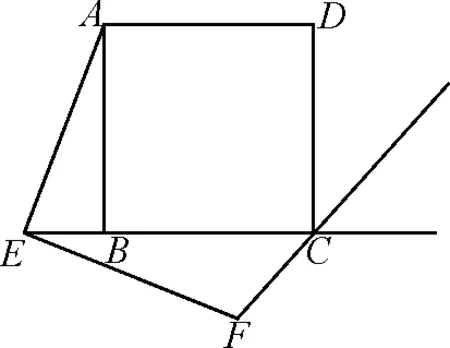
圖6
引導5:變式后的圖形看上去變得復雜,但方法還是可以遷移過來的,我們還會考慮哪兩個三角形全等?需要構造哪個三角形?圖上標記出△ECF,想想如何構造△AGE?同學們試試,待會請同學分享你的探究結果.
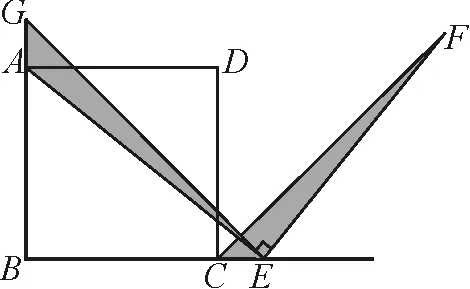
圖7
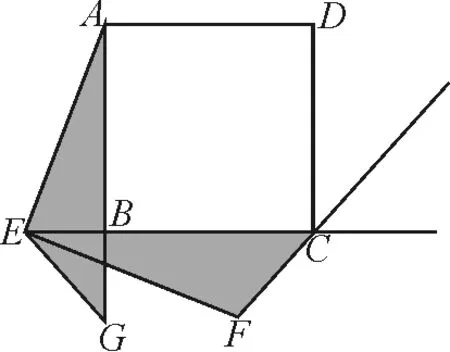
圖8
設計意圖:學生通過這樣的嘗試畫圖,如圖7和圖8,對畫圖和分類討論、遷移能力等有更深的體悟.給足學生畫圖探究的時間,學生的思維才會在經歷的過程中留下成長的足跡.在學中做,在做中學,是學生最喜歡的成長方式.同時點G的尋找,也可以看成點E繞點B逆時針旋轉90°,構造等腰直角三角形而得到.
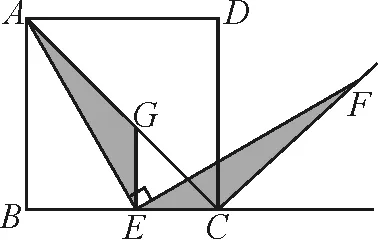
圖9
引導6:如圖1,構造與△ECF全等的三角形還有其他方式嗎?這里有AE⊥EF,又需證明AE=EF,說明AE與EF是既垂直又相等,是否聯想到把△ECF繞點E旋轉90°這個思路來構造全等三角形呢?如圖9,把點C繞點E逆時針旋轉90°到點G,連接AG,是否能證明△AGE≌△FCE?
引導7:如圖9,易證∠AEG=∠FEC,EG=EC,其中∠ECF=135°,如何推導∠AGE=135°,即需要證明點A,G,C共線.進而能深入思考:由∠ECG=45°和∠ACB=45°得點A,G,C共線.如果不去證明A,G,C三點共線,而是過點E作EG⊥BC交AC于點G,那么能證明△AGE≌△FCE嗎?試一試,再分析圖10和圖11的情況.
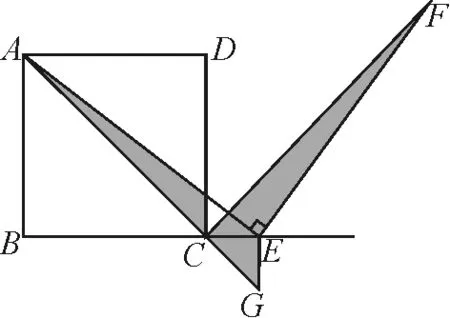
圖10
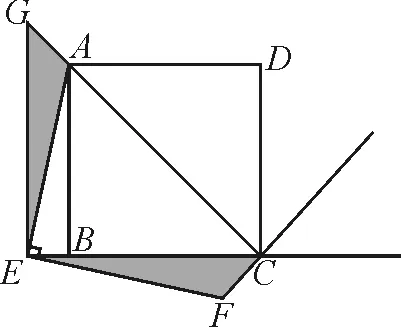
圖11
引導8:我們把△AEC繞點E順時針旋轉90°去構造和△ACE全等的三角形,即過點E作EG⊥BC交CF或其反向延長線于點G是否可以構造全等三角形解決問題呢?如圖12,挑選一種進行證明.
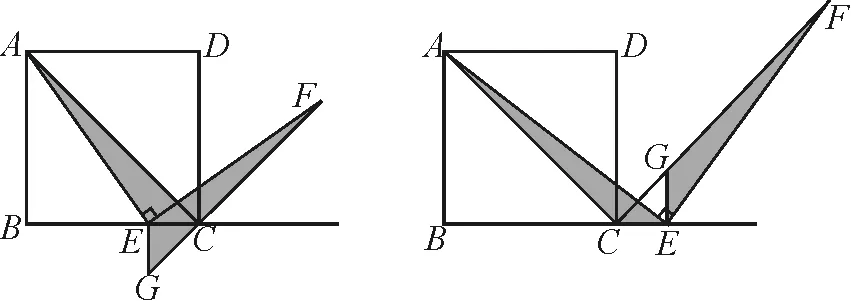
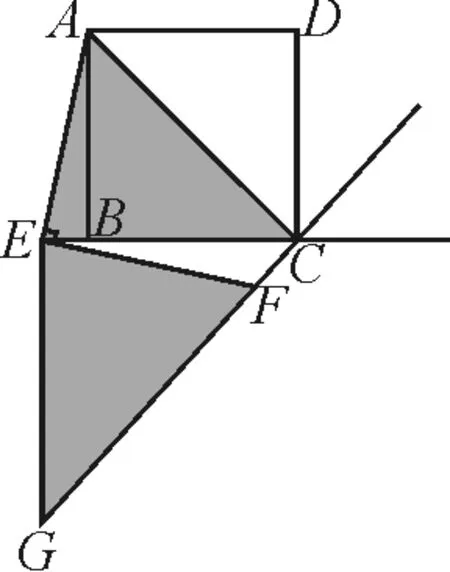
圖12
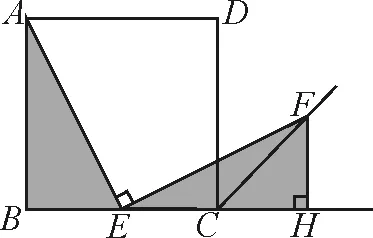
圖13
引導9:能否過點F作FH⊥BC交BC的延長線于點H(如圖13)去證明AE=EF?
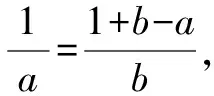
引導10:對于解決正方形、長方形、等邊三角形等特殊的幾何圖形中線段的位置或數量關系,我們也可以將圖形放入直角坐標系內研究,運用兩直線垂直時,兩條直線的斜率之積為-1及兩點之間距離公式也可以解決這個問題.大家可以嘗試幾何問題代數化求法.
設計意圖:本題的證明可以構造手拉手型模型、一線三等角模型等來解決,讓學生感悟模型的構造,能用數學模型的眼光觀察幾何圖形,發現隱性的數學模型,從而使解題有章可循,有法可依,又能從多個角度思考問題,培養思維的多樣性.
分析:(1)如圖12.
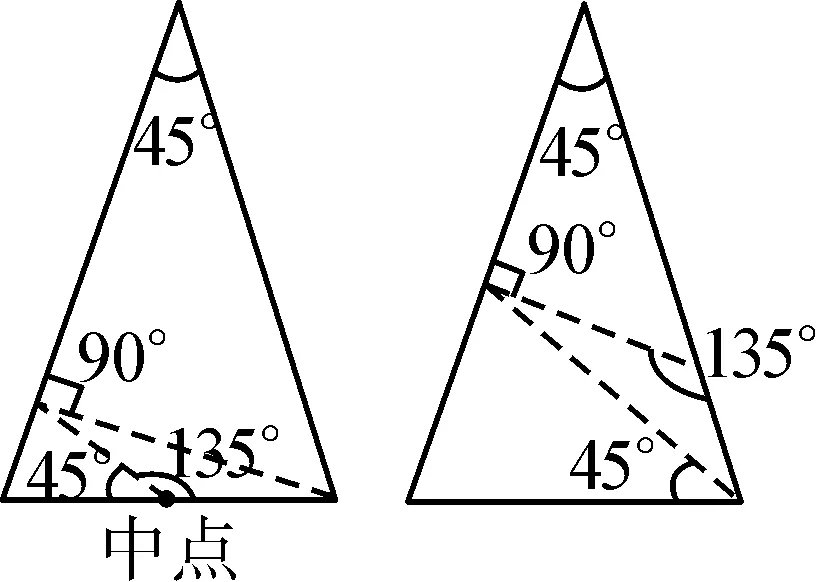
圖12
(2)如圖13和圖14.
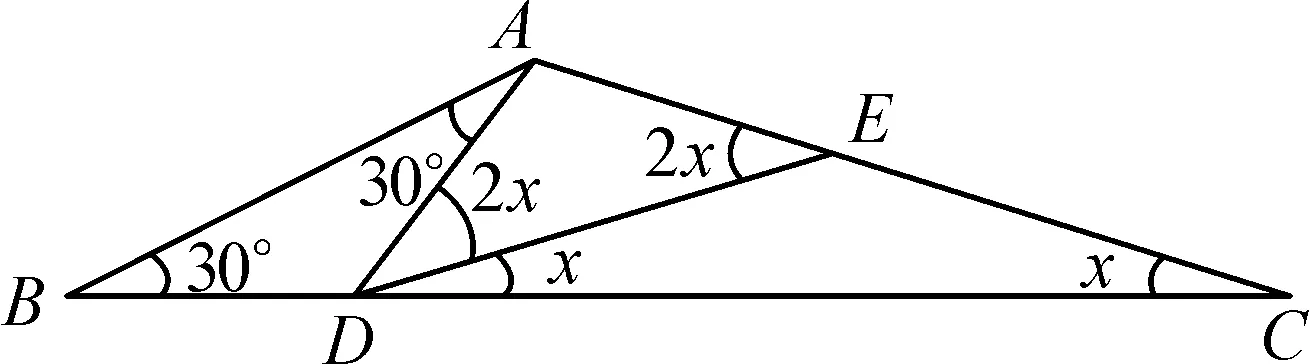
圖13圖14
①當AD=AE時,由2x+x=30°+30°,得x=20°.
②當AD=DE時,由30°+30°+2x+x=180°,得x=40°.
所以x的值是20°或40°.
點評:從上面的探究可以發現,利用方程和角之間的關系,可求解有關角的問題.
本文從形、點、線三個方面探討了三角形的新定義問題.一方面,開闊了學生的視野,從新的視角關注三角形中一些特殊的點與線段,它屬于知識新的增長點;另一方面,將舊知識融合在新知識里,發揮舊知識在解決新問題時的價值,提高了學生創造性解決問題的能力.Z

