巧用常數 化簡根式

?甘肅省天水市秦州區太京中學 劉 杰

1 巧設常數

分析：觀察二次根式中的被開方數，它們是四個連續的奇數的積與16的和，直接計算，幾乎不可能．若用字母來代替某個數，其他的數字可以用含有這個字母的代數式表示．這樣就把復雜的數字問題轉化為相對簡單的含字母的代數式問題，運用乘法公式計算即可．

解：設3 633=a，則

=a2-2a-4-a2+1=-2a-3

=-2×3 633-3=-7 269.

點評：用字母來表示數，是數學里重要的數學思想和解題策略，是創新思維，是靈活運用數學知識與方法的體現．

2 巧拆常數

筆者8：30到塘口，池塘面積9畝，池塘邊坡露出水面50～60cm，水淺，1.3m左右；伸手入水估測透明度15cm，水色濃綠色。鰱、鳙、草魚、鯽一共放4000尾左右。一星期前有人來塘口撒網取樣，第二天發覺有1尾草魚死亡，鄰居說是爛鰓，給了7瓶藥，進行治療，治后仍有零星死亡。飼料投撒后，池魚也不像以前爭著搶，光在周圍轉，不吃。是不是拉網嚇的？問其藥瓶是否還在？找出一看，180mL/瓶，標明治療量20～30mL每畝每米水深，未具體標明成分，殺蟲同時有部分消毒功能。按常規2瓶即可，而實際使用了7瓶，超出5瓶，施藥可能有中毒風險。

點評：根據數字特點，將原數據拆分、分組、組合，再因式分解，約分是二次根式運算的常用解題策略．

3 巧添常數

點評：使用乘法公式和運算律進行計算，是初中代數最基本的運算技能，在整式，分式、二次根式計算中必不可少．

4 巧代常數

點評：因式分解是中學數學里最重要的恒等變形之一，是解決很多數學問題的有力工具．我們要根據數字特點，發現數字間蘊含的數字規律，再使用因式分解化簡，使難題變易．

5 巧比常數

點評：本題的解答運用了等比性質、分式的乘方、積的乘方等計算公式，特別是根式部分的化簡，要用整體的眼光去分析解決．

6 巧乘常數

點評：熟悉三個數和的完全平方公式，并洞察數字結構是解決本題的關鍵．在解決問題時，不妨先分析數字特征，再聯想數學知識與方法，最后進行變形轉化，直至問題解決．

7 巧除常數

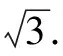
點評：審視題目的結構，能夠化簡的先化簡．化簡是為了使數字特點更加明顯，方便使用公式進行變形，從而簡化運算．

8 分組常數

點評：根據數學題目自身結構的特殊性，從整體角度去觀察分析，靈活轉換題目數字．本題就是運用整體思想進行約分．其中將分子的數字分組是實現目標的關鍵．

綜觀以上例子，一些二次根式的化簡題看似復雜，若根據題目的數字結構特點，多觀察分析，多聯系思考，合理變形，優化算法，也可以快速求解．這樣可以培養學生的創新意識和探究精神，更能提高學生分析問題、解決問題的能力，切實提升學生的數學素養．Z