以問題驅動解題方法的形成
——以一道一次函數題的教學為例
?江蘇省南通市幸福中學 陳 宇
學生“一聽就懂,轉眼即忘”的現象,在初中數學教學中時有發生.為了避免這種現象,筆者在教學中經過多重實踐,發現問題的提出能驅動解題方法的形成,并對獲得知識的內涵具有重要作用.實踐表明,教學活動中的問題能厘清學生的思維,幫助學生理解知識的內涵,建構新的知識結構.為此,筆者以一道一次函數題的教學為例,具體談談怎樣將“方法形成”落實到問題教學研究中.
1 巧妙導入,拋出問題
俗話說:“良好的開端是成功的一半.”課堂導入作為教學活動的初始環節,具有吸引學生注意力、激發學習興趣等重要作用.教師在課堂導入時,緊扣學生的心理特點,設置具有一定挑戰性的問題障礙,能有效地推動學生的學習動機,讓學生不由自主地產生學習行為.因此,巧妙地導入難度適中的問題,在教學活動中具有拋磚引玉的功效.
案例如圖1,已知點A的坐標為(0,3),點B的坐標為(4,6),點P是x軸上的動點,若點B關于AP的對稱點B′正好落在x軸上,試求點P的坐標.
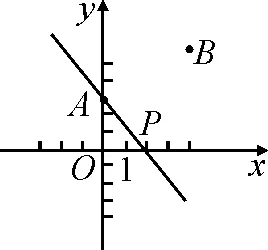
圖1 圖2
分析:解決此題的主要障礙在于AP為一條動直線,點B′為一個動點.一般情況下,我們可從以下兩種思路著手解決問題.
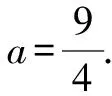
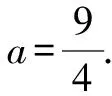
本題難易程度適中,學生稍加思考即能分析出解題方法.學優生都能想到這兩種方法,大部分學生至少能想到一種解題方法.此問題的難度并不大,落在大部分學生的最近發展區內,學生對此題表現出較高的探索興致.一些基礎較薄弱的學生也躍躍欲試,基本能滿足學困生“跳一跳,摘到桃”的效果.
2 變式探究,激活思維
數學是思維的體操,學習數學的目的在于形成良好的思維,獲得發現、探究與解決問題的能力.為了激活學生的思維,讓學生在解題中形成自己獨特的解題方法,筆者在學生解完上述案例的基礎上,提出新的問題,供學生探究.
新問題的提出需突破思維的局限性,一般采用變式教學的方式拓寬學生的視野,培養學生的創新意識.變式教學一般是指將命題進行合理轉化,常見的有以下幾類:①條件與結論的轉換;②更換命題中存在的一些非本質特征;③將問題的形式與內容進行轉換;④保留原題的本質性因素,設置具有實際應用性的新環境,讓學生從根本上掌握問題的內涵等.
本案例是一道常見題,具有較高的研究價值.因此,筆者提出以下兩個變式問題,供學生探究與思考,以強化學生的解題思路與方法,為模型思想的發展奠定一定的基礎.
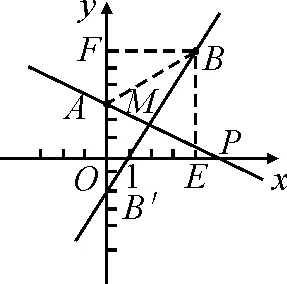
圖3
變式1如圖3,假設題設條件中點B關于直線AP的對稱點B′恰巧在y軸上,則點P的坐標是什么?
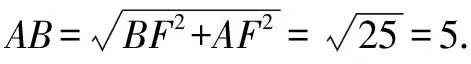
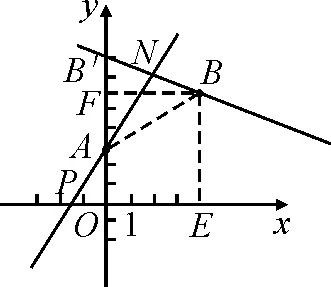
圖4
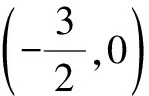
變式2如圖5,已知點A的坐標為(0,2),在其他所有條件都不發生改變的情況下,點B′正好位于x軸上,點P的坐標是什么?
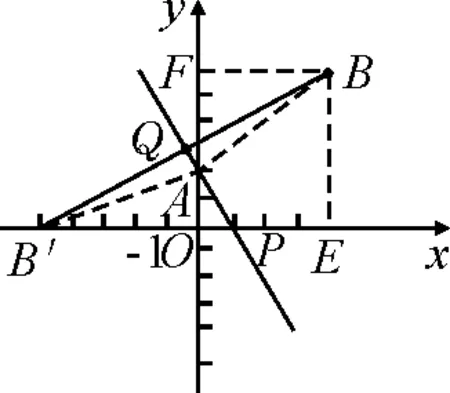
圖5
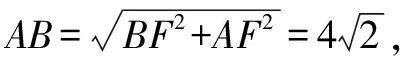
在原題的基礎上,筆者以變式的方式提出新的探究方向.先討論點B關于直線AP的對稱點B′在x軸上的情況,再討論該點處于y軸上的情況.循序漸進地提出問題串,既符合學生思維由淺入深的發展規律,又充分體現了問題的層次性,這種方法能有效地培養學生的類比思想.
有梯度地設計帶有導向性的問題,能讓學生自主發現問題間的內部聯系,從而產生探究的動力,當問題更上一個臺階時,學生的思維也得到有效開發.此過程中,學生在教師的引導下,經討論與探究獲得相應的解題方法,有效地培養了學生的類比思想、數形結合思想,為練習訓練的開展與模型思想的形成奠定了堅實的基礎.
3 適當練習,建構模型
練習具有鞏固所學內容、提升思想認識與促進創新等作用.過多的練習(題海戰術)會讓學生對學習產生厭倦感,過于簡單的練習又達不到提升各項數學能力的效果.因此,教師在課程結束后,應根據內容與學情設計難易程度適當的練習,讓學生在解題訓練中完成認識上的飛躍,以促進認知的發展.
可見,練習并非漫無目的地刷題,而是適應新課標所倡導的化歸演練,以突出解決類似問題為主的訓練.化歸演練比傳統練習更具探索性、挑戰性與開放性,學生通過化歸演練能在大腦中建構新的模型,激發各類數學思想的形成與發展.
練習如果點A與點B的坐標分別為(0,a)與(b,c),且a,b,c均大于0,2a-c≠0,在案例中其他條件都不變的情況下,求點P的坐標.
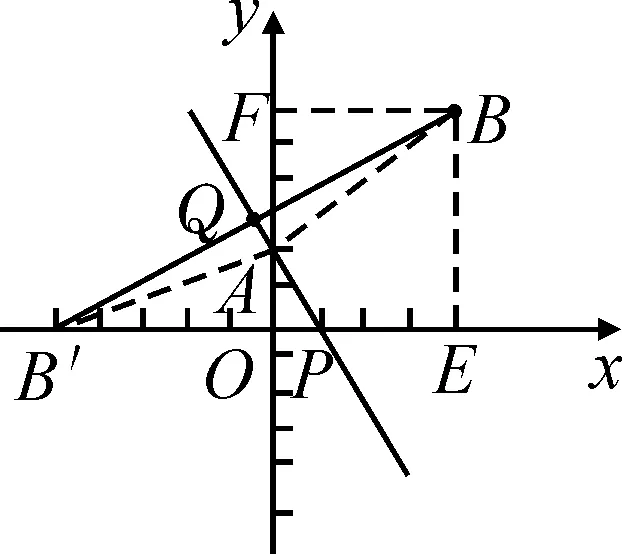
圖6
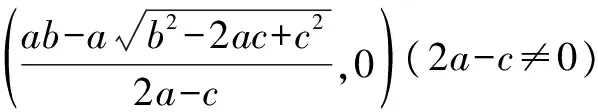
例題教學的目的不在于學會解決一道題,而在于探尋解決此類問題通用的數學思想與方法.本題用字母的表示來揭示問題的規律,形成了解決同類問題的模型,有效地激活了學生的模型思想.該題屬于典型的化歸演練,學生解決該問題的過程就是構建模型的過程.今后若再遇到類似的問題,則能快速地找出解題方法,從真正意義上實現了舉一反三、以一通百的教學目的.
總之,解題方法的形成,離不開問題的驅動.不論是課堂導入,還是變式的探究,抑或是化歸演練,都離不開問題的引導.這些問題猶如一級級臺階,學生以問題為落腳點,在拾級而上的過程中,實現數學思維的螺旋式上升,為數學思想的形成與解題能力的提升奠定了堅實的基礎.

