直線參數方程及其應用淺析
?重慶市涪陵高級中學校 張雨靈
1 引言
直線與二次曲線相交、相切、相離等位置關系的判斷以及由此引出的系列問題是高中解析幾何專題要討論的問題,這些問題是訓練學生邏輯推理、數學運算、直觀想象等核心素養的重要載體.解析幾何的基本思想是用代數的方法來研究解決幾何問題,所以在求解解析幾何相關問題的過程中往往需要大量計算,這是解析幾何問題的主要難點所在.而突破這一難點,除了需要充分挖掘利用幾何信息簡化計算外,有時還需根據具體問題合理選擇直線或曲線方程的形式.比如,利用直線方程參數形式,不僅可以在解決二次曲線和直線相交時的求點坐標、距離、弦長、弦的直線方程等系列問題中簡化計算,而且還可以有效解決與弦的中點有關的軌跡方程,以及曲線的切線方程等問題.下面先探討直線的參數方程中參數t的幾何意義及其應用.
1.1 直線參數方程中參數t的幾何意義
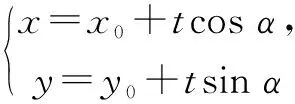
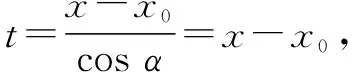
1.2 聯立直線與二次曲線方程
設缺xy項的一般二次曲線Γ的方程為Ax2+Cy2+Dx+Ey+F=0(其中A,C不同時為0),聯立二次曲線Γ與直線l的參數方程,得
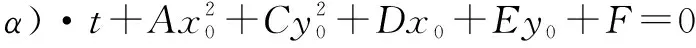
(*)
不妨記
m=Acos2α+Csin2α
①
n=2Ax0cosα+2Cy0sinα+Dcosα+Esinα
②
③
則(*)式可簡記為
mt2+nt+w=0.
④
下文將運用直線l的參數方程并結合參數t的幾何意義,解決直線l與二次曲線Γ的常見問題.
2 判斷直線l與二次曲線C的位置關系
將直線l的參數方程與二次曲線Γ聯立,整理的方程記為④,則其判別式為Δ=n2-4mw.當Δ>0時,直線l與二次曲線Γ相交;當Δ=0時,直線l與二次曲線Γ相切;當Δ<0時,直線與二次曲線Γ相離.
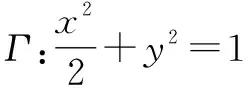
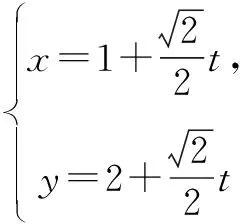
由Δ=8>0知,直線l與橢圓Γ相交.
3 直線與二次曲線的交點或弦長問題
將直線l參數方程與二次曲線Γ聯立,整理得方程④,當Δ>0時,記兩實根分別為
(1)由直線參數方程中參數t的意義知,t1,t2分別為直線l與二次曲線Γ交點A,B所對應的參數,由此可求出交點A,B坐標為
A(x0+t1cosα,y0+t1sinα),
B(x0+t2cosα,y0+t2sinα).
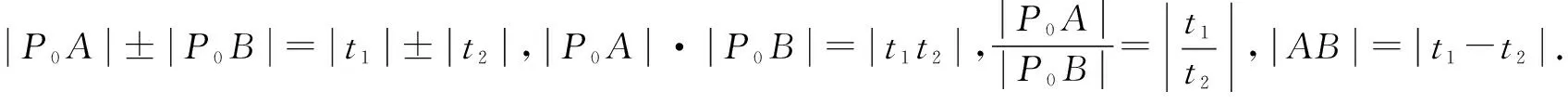
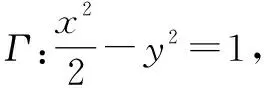

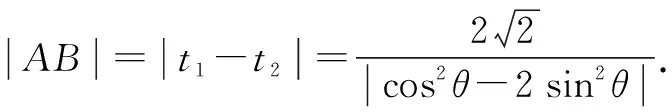
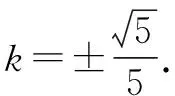
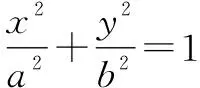
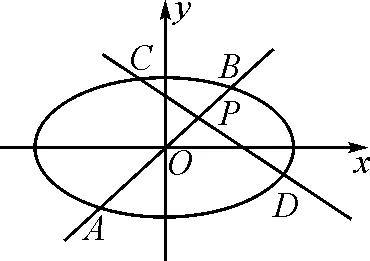
圖1
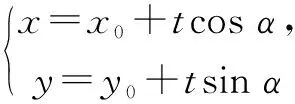
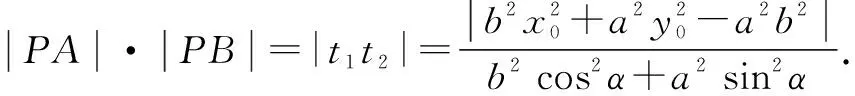
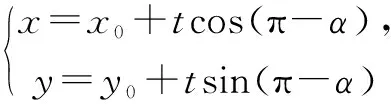
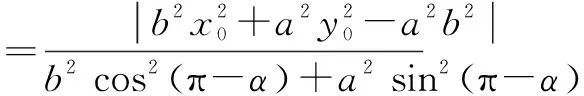
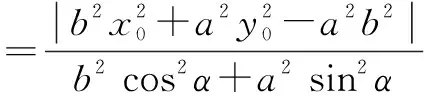
所以|PA|·|PB|=|PC|·|PD|,從而A,B,C,D四點共圓.
4 二次曲線Γ中與弦中點有關的問題
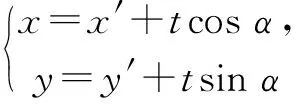
4.1 求二次曲線Γ平行弦中點所滿足的軌跡方程
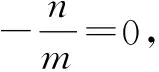
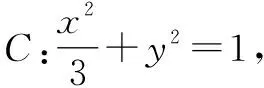
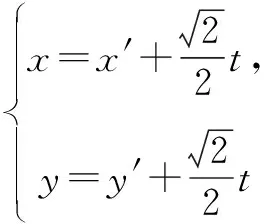
因為M(x′,y′)為中點,所以有t1+t2=0,即x′+3y′=0.所以中點M的軌跡方程為x+3y=0.
4.2 求二次曲線過定點P(x0,y0)的弦的中點的軌跡方程
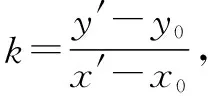
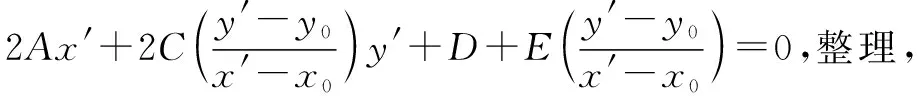
2A(x′)2+2C(y′)2-(2Ax0-D)x′-(2Cy0-E)y′-(Dx0+Ey0)=0
①
即中點M(x′,y′)坐標滿足①式,即得中點M的軌跡方程.
當動弦的斜率不存在時,聯立直線x=x0及二次曲線方程,求出交點坐標,再求出中點,通過驗證中點是否滿足斜率k存在時的方程①來決定是否需要補充這一點.
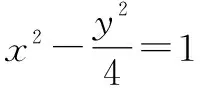
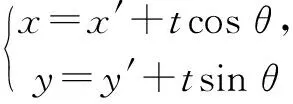
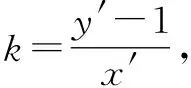
當直線l的斜率不存在時,直線與雙曲線無交點.
綜上所述,弦中點的軌跡方程為4x2-y2+y=0(y<4或y≥1).
5 求二次曲線Γ的切線方程
5.1 求過某定點P(x0,y0)的二次曲線Γ的切線方程
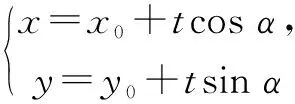
例6過點P(-1,2)作拋物線y2=2x的切線,求此切線方程.
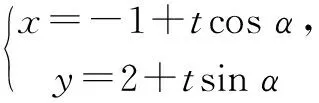
5.2 求二次曲線Γ的斜率(或傾斜角)已知的切線方程
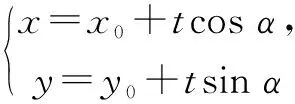
例7求二次曲線ax2+by2=1,(a>0,b≠0)傾斜角為α的切線方程.
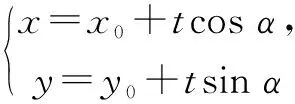
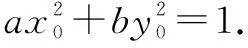
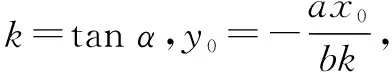
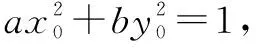
6 結論
通過上文分析討論,我們發現應用直線方程的參數形式能較好地解決直線與二次曲線位置關系的判斷、直線與二次曲線交點、弦長、弦中點、切線等系列問題,并能避免繁雜的運算,拓寬學生視野.

