庫水位變化速率對非飽和邊坡穩定性影響分析研究

翁新海，王家鵬，翁郁馨

（1.浙江省水利水電勘測設計院，浙江 杭州 310002；2.浙江大地巖土勘察有限責任公司，浙江 杭州 310002；3.東南大學研究生院，江蘇 南京 210096）

1 概述

庫水位變化是水庫區滑坡失穩關鍵因素，引起破壞性極大，造成的損失巨大，如著名瓦依昂水庫庫區滑坡造成生命財產巨大損失。因此，研究庫水位變化對非飽和邊坡的穩定性具有重要的現實意義。以西北部庫區邊坡為例，使用Geo-slope 有限元計算軟件，進行滲流分析及穩定性計算。分析不同庫水位上升和下降幅度對非飽和邊坡滲流場和穩定性的影響規律。

2 飽和—非飽和滲流研究現狀

土中水的滲流研究歷史悠久。早在1856 年，法國工程師達西Darcy 提出了線性滲流的達西定律。1889年，俄國的茹可夫斯基首先推導了滲流的微分方程。1922 年，俄國學者巴普洛夫斯基提出了求解滲流場的電模擬法。由于滲流的微分方程在復雜邊界條件下很難得到其解析解，所以人們力圖用數值算法解決它。1910 年，英國學者理查森首先提出了有限元法。在20世紀70年代之后，由于計算機及計算技術的迅速發展，人們開始廣泛應用有限元法、邊界元法和許多其他計算方法計算解決滲流問題。

Frediund 對飽和—非飽和土坡滲流問題做了較完整的論述，把非飽和土壤水運動理論與非飽和土固結理論相結合，得到了飽和—非飽和滲流控制方程，并運用二維有限元方法對復雜地下水流動系統的幾個暫態滲流實例問題進行了數值模擬等[1]。

吳夢喜、高蓮士[2]對飽和—非飽和土體非穩定滲流做了數值分析，對一般的非飽和滲流有限元計算方法加以改進，以消除非飽和滲流數值計算存在的數值彌散現象。同時還提出了一種逸出面處理的新方法，并給出了非飽和非穩定滲流計算的實例。

針對水位降落所引起的邊坡內滲流場的研究，目前采用最多的是以非飽和土理論為基礎，采用有限元法進行分析。時衛民等[3]以布西涅斯克非穩定滲流基本微分方程為基礎，給出了坡前水位降落情況下的坡內浸潤線的計算方程,并進一步利用多項式擬合原理對其進行了簡化，使其變的易于應用。

朱軍等[4]對常用的飽和—非飽和三維多孔介質非穩定滲流的有限元算法進行了改進，提出以高斯點為研究對象。在單元中不同的高斯點有不同的壓力水頭，進而可得到不同的滲透系數k及水體積變化系數，這樣修正得的滲透矩陣和貯水降雨條件下飽和—非飽和土坡的穩定分析矩陣比一般方法更合理。

張培文等[5]在進行飽和—非飽和滲流模擬時，克服了傳統降雨邊界處理方法的缺陷，考慮了降雨過程中地表邊界的條件轉化，為以后的徑流滲流耦合的模擬打下了良好的基礎，為降雨誘發滑坡研究提供了定量的分析手段。

3 飽和—非飽和滲流問題的數學描述及邊界條件

求解飽和—非飽和滲流問題，需要建立其控制方程和邊界條件。在飽和—非飽和滲流分析中，定解條件方程表達式為：

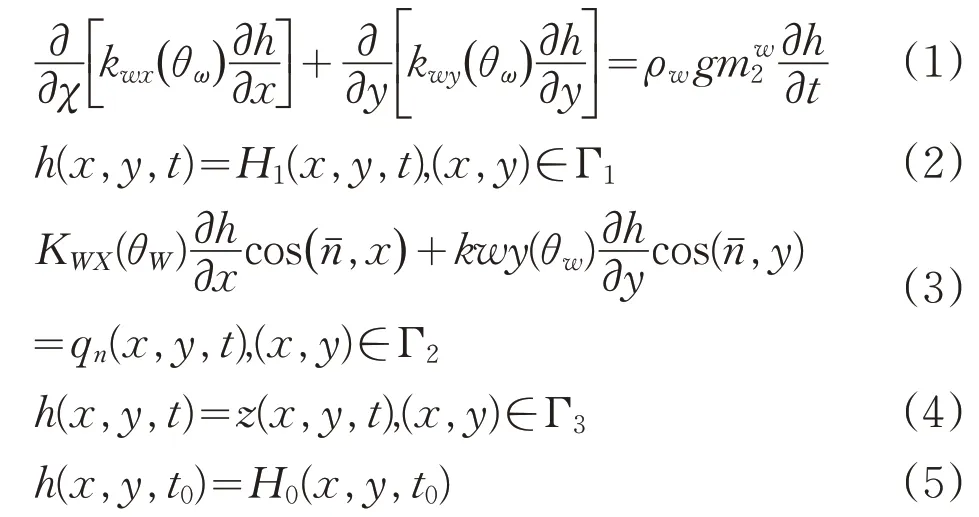
式中：Γ1——水頭分布規律已知的邊界；

H1——邊界水頭，式（1）稱為第一類邊界條件；

Γ2——流量清況已知的邊界；

qn——單位時間邊界法向流量；

Γ3——滲出面邊界；

z——滲出面節點坐標，式（4）可以歸為第一類邊界條件；

H0——初始滲流場水頭，式（5）為初始條件。

在邊界節點處規定水頭為第一類邊界條件，而規定通過邊界的流量稱為第二類邊界條件。正的節點流量表示節點處有入滲，負節點流量表示該節點處有蒸發或蒸騰，當通過邊界的流量為零時，表示不透水邊界。

4 工程實例分析

4.1 邊坡概況

邊坡分布于南側分水嶺一帶，邊坡分布高程1080～1450m，在平面上似橢圓形，其長軸方向為NW向，長約900m，中上部最寬處約694m。邊坡后緣地形較陡峻，坡度40°～60°，中部地形較平緩，坡度25°～30°，前緣地形較陡峻，坡度60°，總體形態上呈上陡中緩下陡的折線狀，總體方量約3100×104m3。

邊坡表部，上部樹木較粗較大，有的樹齡已達數百年，但未見馬刀樹和醉漢林，表部未見裂縫，說明該邊坡形成時間較久遠，現狀處于穩定狀態。

邊坡上游邊界發育有干溝近代沖溝，頂部寬，下部窄，溝底縱坡覆蓋層薄，基巖面有起伏，而成臺階狀分布。下游邊界也為干溝，溝底無水，僅長時間降雨時才有水，此外邊坡內有一條順坡向切割深度3～15m 寬，寬20～30m小沖溝，無水，長時間降雨都無水。

4.2 數值模擬

對邊坡根據地質勘探成果進行有限單元格劃分，綜合考慮計算精度和計算時長。邊坡巖土體對庫水位較敏感，同時邊坡底部與巖體接觸帶比較敏感，這些部位也進行了加密。有限元網格模型如圖1所示。

圖1 有限元網格模型

4.3 巖土體物理力學參數

經現場和室內試驗及工程地質類比法，邊坡體巖土體物理力學參數見表1。

表1 巖（土）體物理力學參數

4.4 計算工況與結果

水庫邊坡應該考慮水庫蓄水對邊坡地下水的影響，地下水水位線上的部分設置容重時應采用天然重度進行計算，而地下水位線以下的部分采用飽和重度進行計算。根據庫區水位運行調度資料，水位緩慢上升速度為每天0.5m，經過30d 從枯水位1155m 上升到1170m：水位上升為每天2m，經過7.5d從枯水位1155m上升到1170m；水位緩慢下降速度為每天0.5m，經過30d 由蓄水位1170m 降低到1155m。水位快速下降時為每天2m，經過7.5d 從蓄水位1170m 降低到枯水位1155m。故分別設置以下4種工況進行模擬：工況1：水位上升速率為0.5m/d；工況2：水位上升速率為2m/d；工況3：水位下降速率為0.5m/d；工況4：水位下降速率為2m/d。

4.4.1 庫水位上升階段

首先對邊坡在枯水位1155m 處進行穩態滲流分析。枯水位1155m處孔隙水壓力分布圖隨著庫區水位上升，地下水位線也逐漸上升，坡內孔隙水壓力也隨之上升。

經過枯水位1155m上升到蓄水位1170m進行滲流模擬，可以了解到每天滑坡體的滲流狀況以及地下水位線，如圖可以看到，庫區水位上升速度高于坡內水位上升速度。可以看出，水位線呈凹形，即坡內水位線低于庫區水位線。主要是因為滑體滲透性小于水位變動速率，滑坡體中水位上升有一個滯后效應，坡內水位變動滯后于坡外水位變動。

通過對邊坡進行穩定性分析，以整個邊坡為研究對象，指定滑動面,經計算可以得到邊坡在水位變動工況下各時段的安全系數，如圖2所示。可以看到隨著水位上升，邊坡穩定性先增強后降低，水位上升速度越快，邊坡穩定性增強越快。水位上升到蓄水后，2m/d時邊坡的穩定性仍然大于0.5m/d 時的穩定性。這是由于坡外水位高于坡內水位，產生指向滑坡體內的動水壓力，有利于邊坡穩定。同時到達蓄水位后，坡內水位與坡外水位慢慢持平，此時指向坡內的動水壓力逐漸降低，以及上層土體基質吸力降低，邊坡穩定性逐漸降低。水位上升0.5m/d 和2m/d 情況下，均是在最高水位處穩定性安全系數最大。由于整個邊坡體型較大，水位上升對整個邊坡穩定性影響較小。

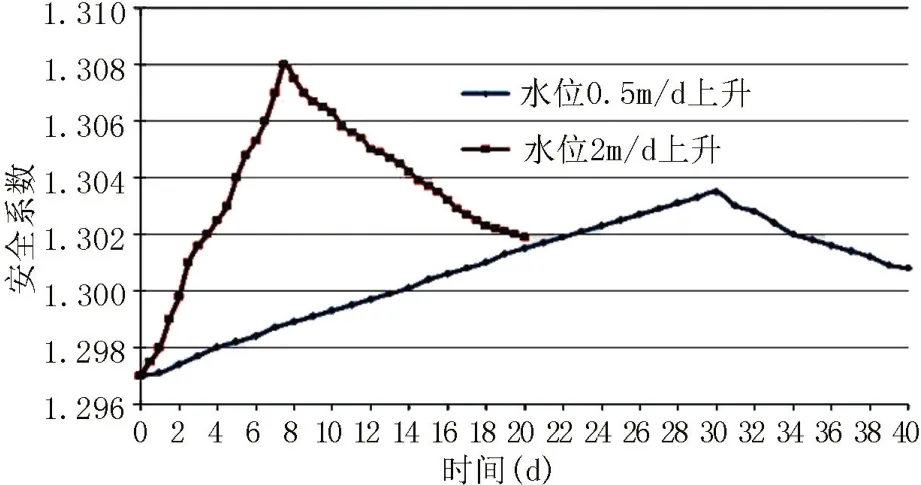
圖2 水位上升整個坡體安全系數圖

4.4.2 庫水位下降階段

首先對邊坡在蓄水位1170m處進行穩態滲流分析（圖3）。隨著庫區水位下降，地下水位線也逐漸下降，坡內孔隙水壓力也隨之下降。水位下降到枯水位1155m時孔隙水壓力分布如圖4所示。

圖3 穩態下處于蓄水位1170m坡體孔隙水壓力分布圖

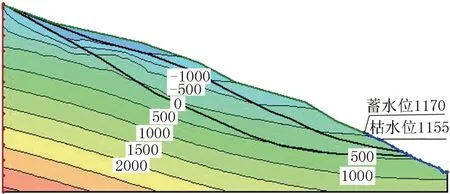
圖4 水位下降到枯水位1155m后孔隙水壓力分布圖

經過蓄水位1170m下降到枯水位1155m進行滲流模擬，可以了解到每天邊坡體的滲流狀況以及地下水位線，可以看到，庫區水位下降速度高于坡內水位下降速度。可以看出，水位線呈凸形，即坡內水位線高于庫區水位線。主要是因為滑體滲透性小于水位變動速率，滑坡體中水位下降有一個滯后效應，坡內水位變動滯后于坡外水位變動。

通過對邊坡進行穩定性分析，以整個邊坡為研究對象，經計算可以得到邊坡在水位變動工況下各時段的安全系數，如圖所示。可以看到隨著水位下降，邊坡穩定性先降低后上升，水位下降速度越快，邊坡穩定性降低越快。水位下降到枯水后，水位2m/d下降時邊坡的穩定性仍然小于水位0.5m/d 下降時的穩定性。這是由于坡外水位低于坡內水位，產生指向滑坡體外的動水壓力，不利于邊坡穩定。同時到達枯水位后，坡內水位與坡外水位慢慢持平，此時指向坡外的動水壓力逐漸降低，以及上層土體基質吸力的升高，邊坡穩定性逐漸升高。水位下降0.5m/d 和2m/d 情況下，均是在最低水位處穩定性安全系數最小。由于整個邊坡體型較大，水位下降對整個邊坡穩定性影響相對較小。

通過對邊坡進行穩定性分析，以局部涉水邊坡為研究對象，得到邊坡前緣涉水段在水位變動工況下各時段的安全系數，如圖5所示。可以看到邊坡安全系數與水位變動同邊坡整體考慮有相同的規律。局部涉水邊坡的特點是在水位變動下，穩定性變化幅度相當大。

圖5 水位下降邊坡整體安全系數圖

5 結論與建議

本水電站堆石壩為2 級建筑物，依據《水電水利工程邊坡設計規范》（DL/T5353-2006），樞紐工程區邊坡為Ⅱ級邊坡，安全系數需滿足表2的要求。

表2 水電水利工程邊坡涉及安全系數

對該水電站庫前非飽和邊坡在水位變動及降雨工況下進行模擬分析，對邊坡整體考慮，具體安全系數如表3所示。可以得出以下結論，邊坡在水位變動均處于穩定狀態，水位變動對邊坡整體穩定性產生了一定的影響，其中水位驟降對邊坡穩定性影響較大，邊坡穩定性下降較多，但邊坡安全系數均大于1.25，邊坡仍處于穩定狀態。

表3 邊坡在不同工況下的最小安全系數

根據有限元數值模擬分析，庫水位按2m/d上升速率，預計8d 左右安全系數達到最大，庫水位按0.5m/d上升速率，預計30d左右安全系數達到最大，對邊坡穩定有利，因此建議在水庫蓄水時可以采用先快后慢運行方式；當水庫泄洪時，按0.5m/d 下降速率，預計30d左右安全系數達到最小，按2m/d 下降速率，預計7d左右安全系數達到最小，因此采用先慢后快運行方式，對邊坡的穩定最為有利。