利用首次積分法求解一致時(shí)空分?jǐn)?shù)階微分方程

王麗真，沈 翔

(1.西北大學(xué) 非線性科學(xué)研究中心,陜西 西安 710127; 2.西北大學(xué) 數(shù)學(xué)學(xué)院,陜西 西安 710127)

隨著科學(xué)技術(shù)的深入發(fā)展,在熱學(xué)、流變學(xué)、材料和力學(xué)系統(tǒng)、信號處理、系統(tǒng)識別、控制科學(xué)、生物科學(xué)、工程學(xué)、氣象學(xué)等諸多領(lǐng)域中,整數(shù)階微分方程已經(jīng)不能滿足人們的研究需求,進(jìn)而分?jǐn)?shù)階微分方程被越來越多的研究者采用。早在300多年前,洛必達(dá)就提出了這樣的問題:什么是二分之一階導(dǎo)數(shù)?這個(gè)問題被后來的諸多科學(xué)家們不斷研究,發(fā)展出了諸多分?jǐn)?shù)階導(dǎo)數(shù)的定義,常見的如Riemann-Liouville型分?jǐn)?shù)階導(dǎo)數(shù)、Caputo型分?jǐn)?shù)階導(dǎo)數(shù),其中，Caputo型分?jǐn)?shù)階導(dǎo)數(shù)在物理領(lǐng)域應(yīng)用更廣泛[1]。但是，前人所定義的微分算子亦有其缺陷,即不滿足整數(shù)階導(dǎo)數(shù)所具備的一些運(yùn)算性質(zhì)。2014年,Khalil及其合作者發(fā)現(xiàn)了新的分?jǐn)?shù)階導(dǎo)數(shù)的定義,即一致分?jǐn)?shù)階導(dǎo)數(shù),它具有許多經(jīng)典微積分的性質(zhì),如半群性質(zhì)、復(fù)合函數(shù)的鏈?zhǔn)椒▌t[2]。2015年,Abdeljawad等人研究了一致分?jǐn)?shù)階微分算子的半群性質(zhì)[3]。2015年,?enesiz等人研究了基于一致傅里葉變換下的一致分?jǐn)?shù)階時(shí)空熱方程的解[4]。2016年,Benkhettou等人研究了任意時(shí)間尺度上的一致分?jǐn)?shù)階微積分問題[5]。2016年,Mehmet等人研究了一致分?jǐn)?shù)階積分的Gr?nwall型不等式[6]。2017年,ünal等人采用微分變換法研究了一致分?jǐn)?shù)階常微分方程的解[7]。2017年,Lazo等人研究了一致分?jǐn)?shù)階導(dǎo)數(shù)的變分法[8]。2018年,Thabet等人通過分?jǐn)?shù)階微分變換建立了一致時(shí)空分?jǐn)?shù)階偏微分方程的解析解[9]。2019年,李倩倩研究了一類一致分?jǐn)?shù)階微分方程解的穩(wěn)定性[10]。2021年,閆立梅等人利用不變子空間方法求解了一致分?jǐn)?shù)階導(dǎo)數(shù)模型[11]。

本文介紹了一致分?jǐn)?shù)階微分算子及首次積分法；采用首次積分的方法求解了一類一致分?jǐn)?shù)階時(shí)空偏微分方程——修正的Benjamin-Bona-Mahoney方程(簡稱m-BBM方程)；最后，借助Maple軟件,給出了不同參數(shù)下解的圖像。

1 一致分?jǐn)?shù)階微分算子及其性質(zhì)

定義1給定一個(gè)函數(shù)f:[0,+∞)→。則f的α階一致分?jǐn)?shù)階導(dǎo)數(shù)定義為

定理1若α∈(0,1],且f,g在點(diǎn)t是α階可導(dǎo)的,則有

1)Dα(af+bg)=aDαf+bDαg,?a,b∈，Dα(tm)=mtm-α,?m∈，

2)Dα(f·g)=gDαf+fDαg，

5)Dαk=0,k∈。

2 首次積分法

馮兆生在2002年通過Hilbert-Nullstellensatz定理得到了雙變量的除法定理,從而通過除法定理尋找方程的首次積分[12]。

假設(shè)存在一個(gè)關(guān)于獨(dú)立變量x,y,t的一致分?jǐn)?shù)階非線性偏微分方程

Dαux,Dαuy,uxxx,…)=0,0<α<1。

(1)

首先，做變換

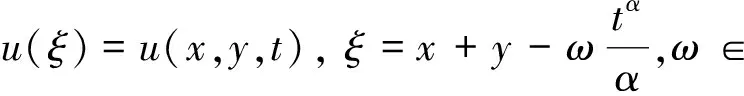
(2)

利用定理1,如下結(jié)論成立:

將上述結(jié)論代入式(1)中,從而得到一個(gè)新的非線性常微分方程:

G(u,u′,u″,u?,…)=0 ，

(3)

其次,定義

X(ξ)=u(ξ)，Y(ξ)=u′(ξ) 。

(4)

由式(3)、(4)引出一個(gè)非線性常微分方程組

由常微分方程定性理論,如果相同的條件下能找到該方程組的積分,那么它的一般解可以直接得到。

定理2(除法定理)假設(shè)P(x,y)和Q(x,y)是C[x,y]關(guān)于x和y的兩個(gè)二元多項(xiàng)式,且P(x,y)在C[x,y]上是不可約的。若Q(x,y)在P(x,y)=0的點(diǎn)都為0,則存在一個(gè)C[x,y]中的多項(xiàng)式G(x,y)，使得

Q(x,y)=P(x,y)G(x,y)。

3 Riccati方程及其精確解

利用首次積分法,通常會(huì)將方程化為一種特殊的常微分方程——Riccati方程。文獻(xiàn)[13]介紹了如下Riccati方程:

U′=r+pU(ξ)+qU2,r,p,q∈,q≠0。

并給出了當(dāng)Δ=p2-4rq<0時(shí),方程的如下精確解:

其中A,B是非零實(shí)數(shù),且滿足B2-A2<0。

其中廣義的三角函數(shù)定義如下:

4 利用首次積分法解一致時(shí)空分?jǐn)?shù)階m-BBM方程

為此考慮如下的一致時(shí)空分?jǐn)?shù)階m-BBM方程

η>0,μ≠0。

(5)

做變換

(6)

對式(6)應(yīng)用定理1,則有

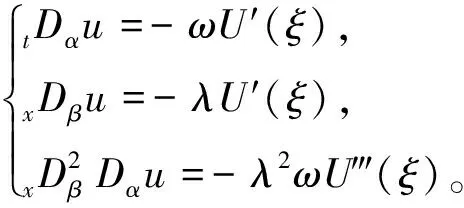
(7)

故原方程式(5)化為

-ωU′(ξ)-ληU2U′(ξ)+λ2ωμU?(ξ)=0,

(8)

對式(8)兩邊同時(shí)積分,并取積分常數(shù)為0,得

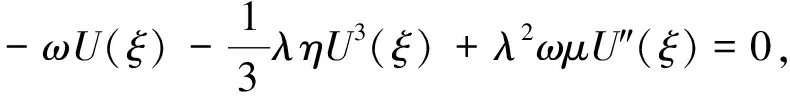
(9)

將式(9)化為

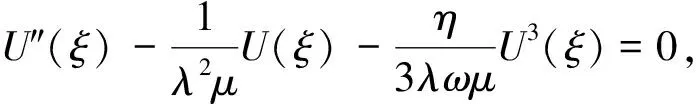
(10)

方便起見,記

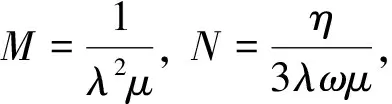
(11)

故式(10)可化為

U″=MU+NU3，

(12)

由式(6),令

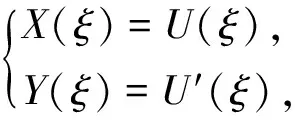
(13)

結(jié)合式(12)、(13)，得到方程組

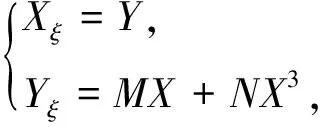
(14)

設(shè)X，Y是方程組(14)的非平凡解,并且存在不可約多項(xiàng)式

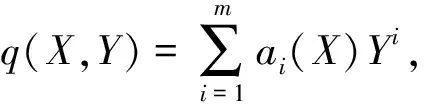
(15)

使得

q(X,Y)=0，

(16)

其中ai(X)(i=0,1,…,m)是關(guān)于X的多項(xiàng)式,并且am≠0。由定理2,存在多項(xiàng)式g(X)+h(X)Y使得

(17)

設(shè)m=1,則可由式(17)，得

a0(X)g(X)+a1(X)g(X)Y+

a0(X)h(X)Y+a1(X)h(X)Y2=

a1(X)·[MX+NX3]，

對比Yi(i=0,1,2)的系數(shù),得到

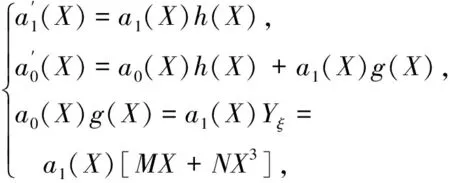
(18)

(19)

對比系數(shù),并由式(11),解得

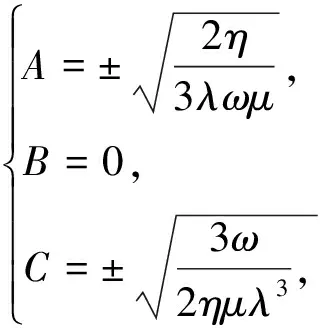
(20)

代入式(15)、(16),得

(21)

再由式(15)、(16),可知

(22)

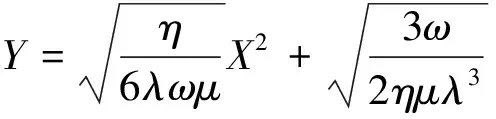
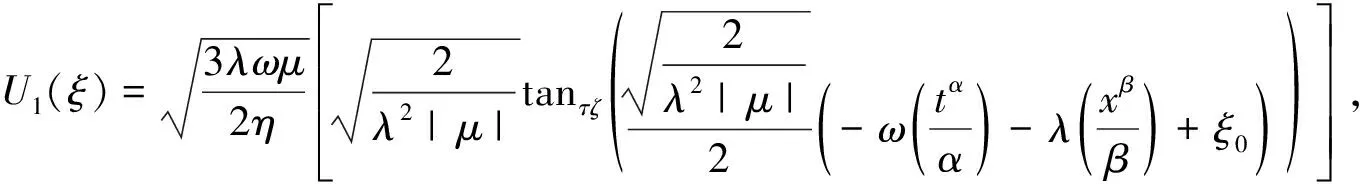
其中，A，B是非零實(shí)數(shù),且滿足B2-A2<0。

5 利用Maple軟件畫出精確解圖像

使用Maple軟件分別畫出了所得部分精確解的圖像,并對比了同一解取不同階數(shù)時(shí)的行為和解的分布情況(見圖1～6)。

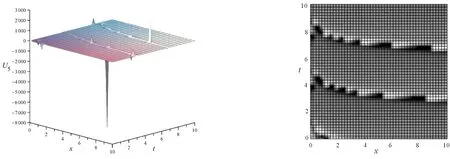
注：λ=1,ω=2,τ=1,ζ=1,α=0.999,β=0.001,ξ0=0,μ=3,η=4圖1 U5 的三維圖和密度圖(β=0.001)Fig.1 3-dimensionalFigure and densityFigure of U5(β=0.001)

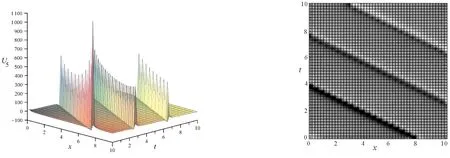
注：λ=1,ω=2,τ=1,ζ=1,α=0.999,β=0.999,ξ0=0,μ=3,η=4圖2 U5的三維圖和密度圖(β=0.999)Fig.2 3-dimensionalFigure and densityFigure of U5(β=0.999)

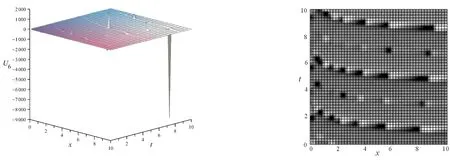
注： 取正號圖3 U6的三維圖和密度圖(β=0.001)Fig.3 3-dimensionalFigure and densityFigure of U6(β=0.001)

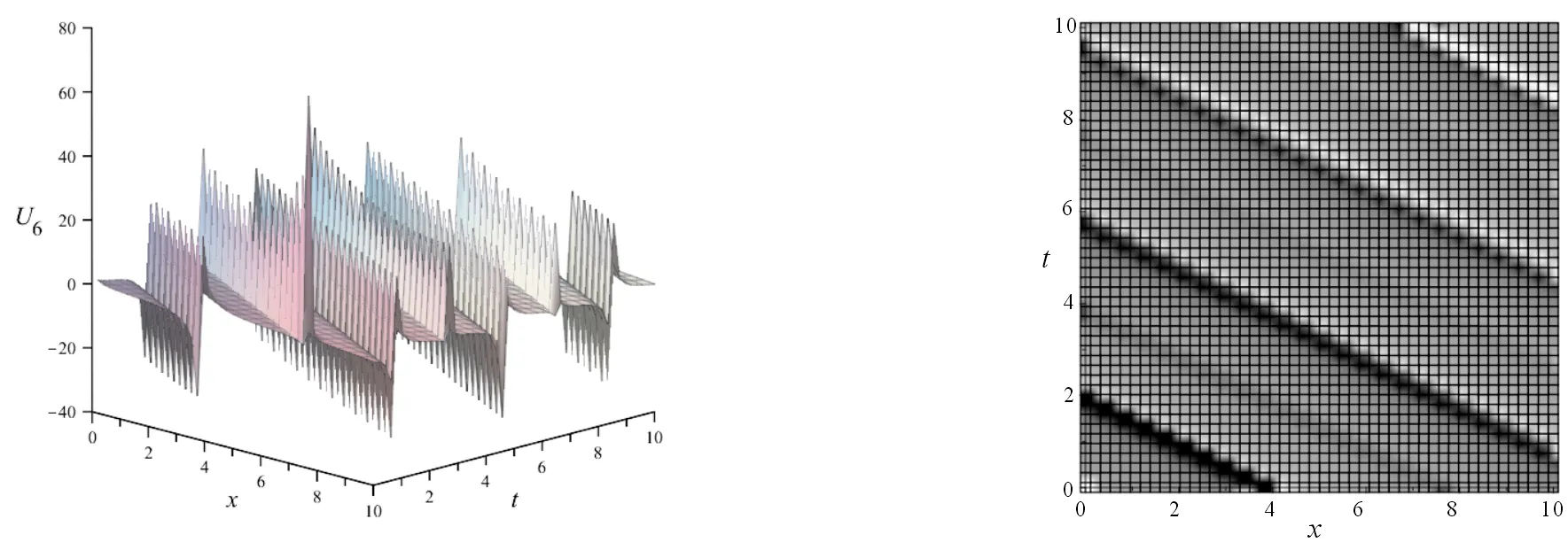
注： 取正號圖4 U6的三維圖和密度圖(β=0.999)Fig.4 3-dimensionalFigure and densityFigure of U6(β=0.999)

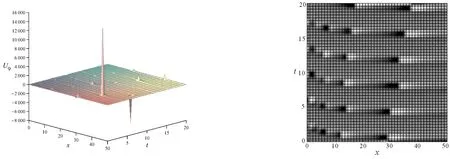
注：λ=1,ω=2,τ=1,ζ=1,α=0.999,β=0.001,ξ0=0,μ=3,η=4圖5 U9的三維圖和密度圖(β=0.001)Fig.5 3-dimensionalFigure and densityFigure of U9(β=0.001)

注：λ=1,ω=2,τ=1,ζ=1,α=0.999,β=0.999,ξ0=0,μ=3,η=4圖6 U9的三維圖和密度圖(β=0.999)Fig.6 3-dimensionalFigure and densityFigure of U9(β=0.999)

通過對比U5、U6、U9的三維圖和密度圖可知，參數(shù)β對解的圖像影響較大。在保持其他條件不變,取β=0.001時(shí),其解整體振幅較小,但是在個(gè)別點(diǎn)的振幅非常大;而取β=0.999時(shí),其振幅始終在一個(gè)相對較小的范圍內(nèi)。

6 結(jié)語

本文主要通過首次積分的方法,構(gòu)造了一致時(shí)空分?jǐn)?shù)階m-BBM方程的精確解。先將偏微分方程化為常微分方程組；再利用除法定理求出解析解；最后，結(jié)合Riccati方程的已知解得到所求方程的精確解。研究表明,首次積分方法對于求解時(shí)空分?jǐn)?shù)階偏微分方程而言是一種簡潔有效的方法。