基于合作創新網絡的復雜裝備協同研發績效分析
康達, 張卓
(南京航空航天大學,經濟與管理學院,江蘇,南京 211106)
0 引言
我國裝備制造業涉及多要素、多主體的技術創新共同作用,不能只依靠單一要素或主體的創新[1]。在技術創新發展過程中復雜裝備制造技術成為必然趨勢。通過分析復雜裝備協同研發績效[2],可以明確復雜裝備協同研發在不同要素環境下的關鍵影響因素,為提高復雜裝備協同研發績效提供參考和依據。目前,對該項目的研究已經成為相關學者研究的重要課題。
李春林等[3]提出考慮了政府對協同研發的影響,構建航空裝備協同研發績效的理論模型,在結構方程模型的基礎上對航空制造裝備共性技術協同研發績效進行評價,根據評價結果實現績效分析。Peykani等[4]從數字化賦能視角,根據“數字化轉型—研發雙元能力—新產品開發績效”理論,構建中小制造企業新產品開發績效的理論模型。采用PLS結構方程和模糊集定性比較分析方法對研究模型進行實證檢驗。為中小制造企業如何有效進行數字化轉型、實現新產品開發績效提供了重要的依據。王丹丹等[5]以物流企業與制造業之間的合作績效作為出發點,該方法通過問卷調查分析并選取評價指標,通過結構方程模型實現兩企業間協同發展的績效分析。
為了進一步提高制造業協同研發績效分析的精度,提出基于合作創新網絡的復雜裝備協同研發績效分析方法,構建合作創新網絡模型,建立協同研發績效指標體系。
1 復雜裝備協同研發績效評價指標體系
1.1 績效機制模型構建
利用合作創新網絡對企業間的網絡進行劃分,分為社會關系和市場關系。社會關系為企業間社會互動的關系,在信息不完全流動的情況下進行潛在利益交換,根據獲得的信息,及時避免風險,發現市場機會[6]。市場關系為交換實質資源。產業網絡組織的命運共同體隨著產業網絡結構越密實對應的共識越高,這有助于建立并維持整體網絡競爭優勢。通過合作創新網絡分析,發現復雜裝備協同研發績效受流程創新、組織文化創新和組織技術創新的影響。
將合作創新網絡分為平穩度、緊密程度、對稱程度、復雜程度和密度等5項變量,構建復雜裝備協同研發績效機制模型,如圖1所示。
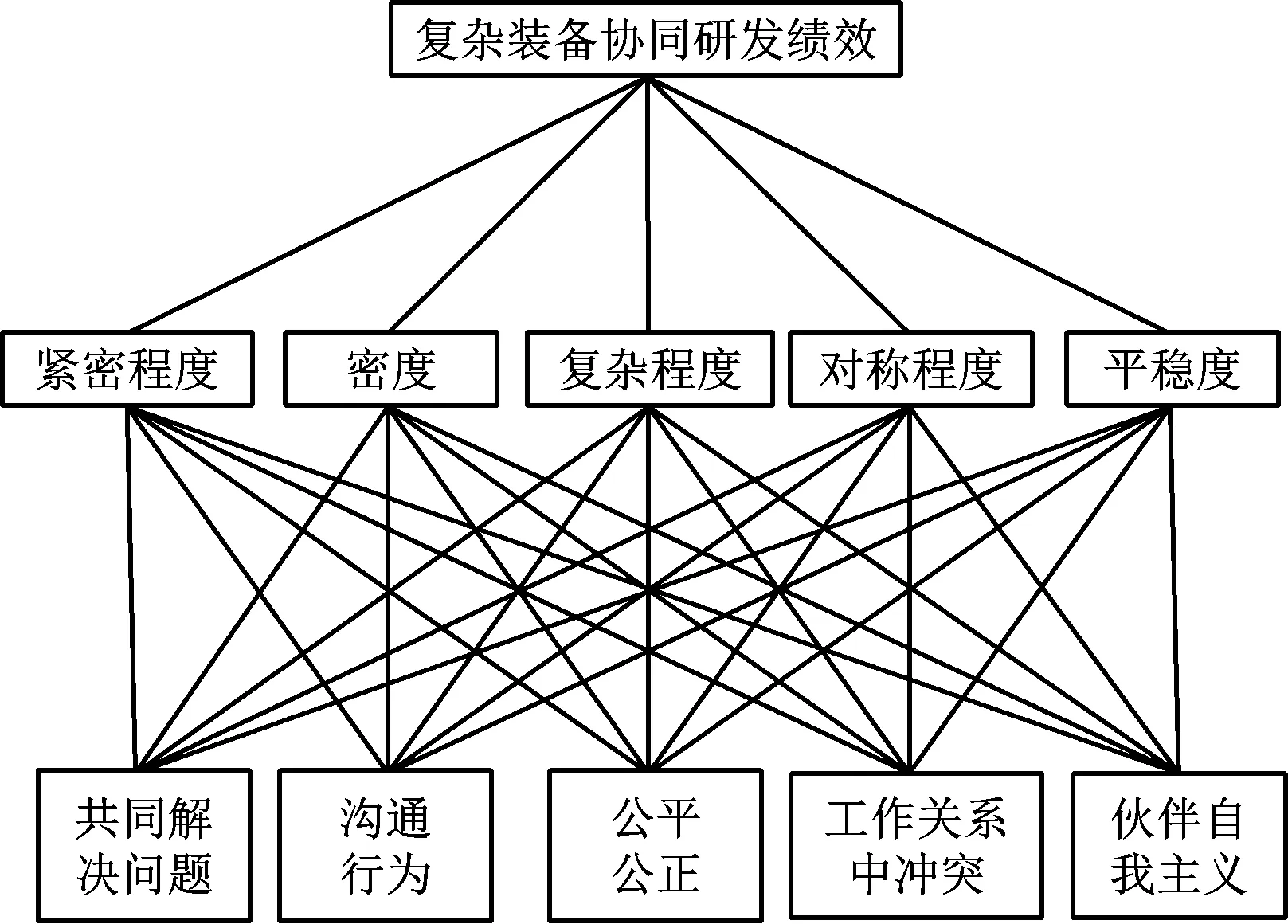
圖1 復雜裝備協同研發績效機制模型
該模型包括測量模型與結構模型2個部分。
(1)測量模型
測量模型的表達式為
(1)
式中,X、Y分別描述的是外源和內生觀測變量,ΛX描述的是外源潛變量上外源指標對應的因子負荷量,ΛY描述的是內生潛變量上內生指標對應的因子負荷量,ξ描述的是外源潛變量,δ描述的是變量X對應的誤差,η描述的是內生潛變量,ε代表的是變量Y對應的誤差。
(2)結構模型
潛變量之間的因果關系可以用結構模型描述,結構模型的表達式為
?=B·Γζ+ζ
(2)
式中,ζ代表結構方程對應的殘差,Γ描述的是內生潛變量受外源潛變量,B描述的是內生潛變量。
1.2 復雜裝備協同研發績效評價指標
基于合作創新網絡的復雜裝備協同研發績效分析方法在復雜裝備協同研發績效機制模型的基礎上建立復雜裝備協同研發績效評價指標體系,如圖2所示。
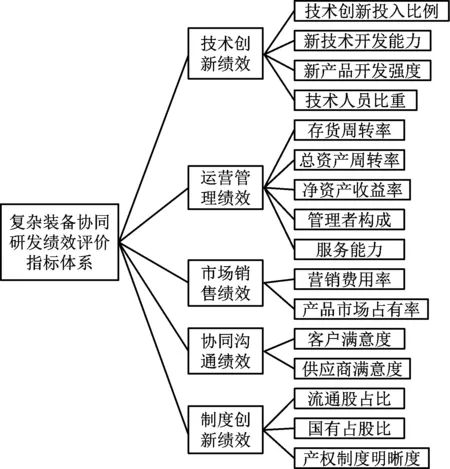
圖2 復雜裝備協同研發績效評價指標體系
2 復雜裝備協同研發績效分析方法
基于合作創新網絡的復雜裝備協同研發績效分析方法利用MaxDEA軟件通過CRR二叉樹(Cox-Ross-Rubinstein,CRR)模型對復雜裝備協同研發績效進行自動評價,根據評價結果實現復雜裝備協同研發績效的分析[7]。
設DMUj代表需要測量的n個電子樣機(Digital Mock-Up,DMU)技術效率,每個數據包絡中存在m種投入,可用xi(i=1,2,…,m)進行描述,vi(i=1,2,…,m)代表投入對應的權重,yr(r=1,2,…,q)代表q種產出,ur(r=1,2,…,q)代表產出對應的權重。
設hk代表的是需要測量的數據包絡DMUk對應的產出投入比,其表達式為
(3)
權重對應的效率值θj通常情況下在區間[0,1]內取值,即
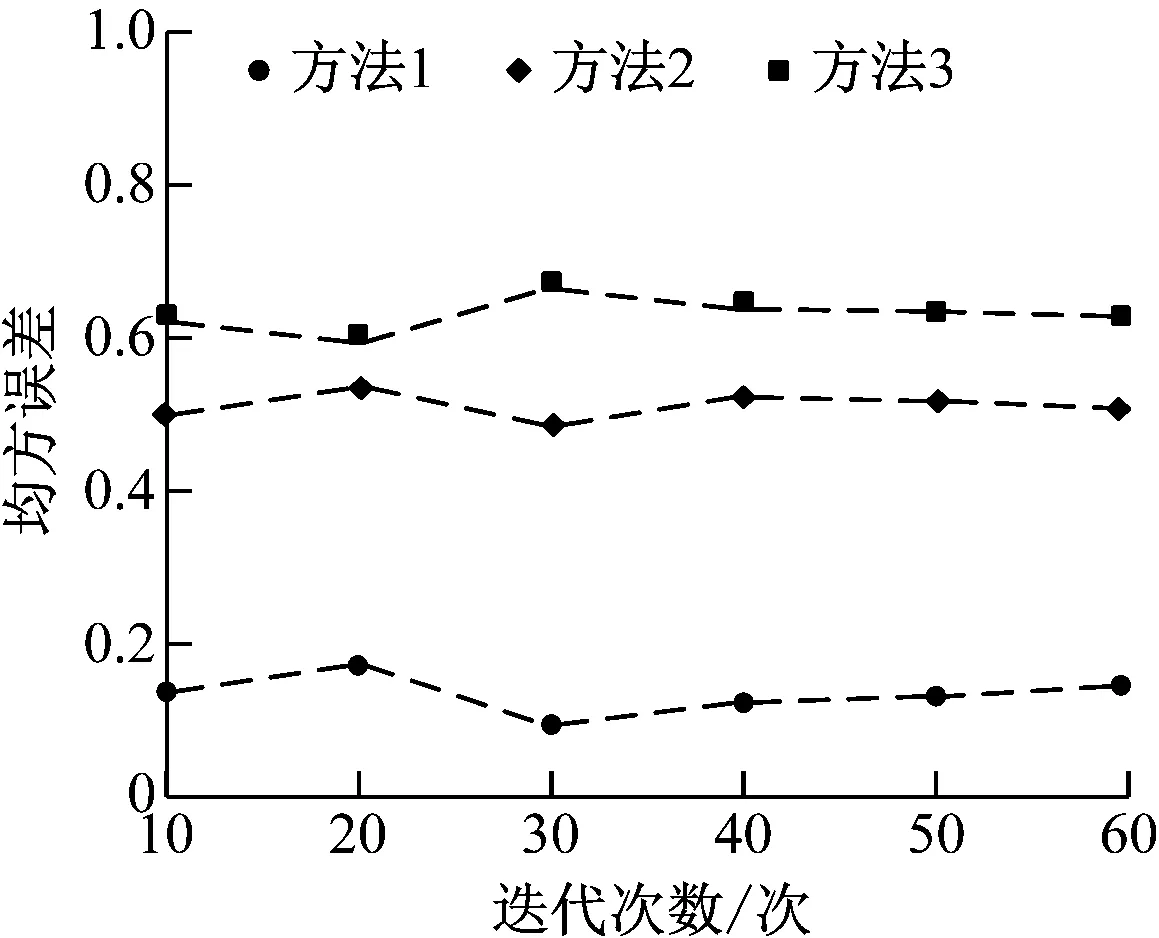
0 (4) 對于連續特征權重的情況,CCR模型的線性表達式為 (5) CCR模型的主要作用是將數據包的效率都控制在1以內,最大化待評價數據包絡的效率值。通過上述分析可知,CCR模型是保守估計數據包絡DMU的無效率狀況。 假設復雜裝備協同研發技術的規模收益保持不變,如果一個數據包絡DMU的投入在技術效率保持不變的條件下變為原來的t倍,對應的產出也提高t倍,即待評價DMUk的產出和投入同時提高t倍,DMUk的技術效率在規模收益不變的前提下保持不變。 設變量u*和v*為式(5)的最優解,則通過上述分析可知tu*和tv*均為最優解。 (6) 令 (7) 則可用等價的線性規劃模型代替CCR模型: (8) 式(8)模型的對偶模型的表達式為 (9) 式中,λ代表的是數據包絡DMU對應的線性組合系數,效率值θ*即為CCR模型的最優解,在區間(0,1]內取值[8]。效率值θ*越小,表示可以壓縮投入的幅度越大,對應的效率就越低。當效率值θ*的值為1時,在前沿面中存在被評價DMU,各項投入在不減少產出的條件下處于技術有效狀態,沒有等比例下降的空間。當效率值θ*小于1時,表明待評價DMU處于技術無效率狀態,各項投入在不減少產出的條件下能夠等比例下降的比例為(1-θ*)。 CCR對偶模型中各項投入在給定產出條件下可以等比例縮減的程度測量無效率的狀況[9],投入導向CRR模型的表達式為 (10) 式(10)模型的對偶模型如下: (11) 式中,φ*為CCR模型的最優解,即復雜裝備協同研發績效評價結果[10]。基于合作創新網絡的復雜裝備協同研發績效分析方法,根據績效的自動評價結果實現復雜裝備協同研發績效的分析。 選取某復雜裝備研發企業利用上述協同研發模型進行實踐,該企業的知識系統包括專家、設計師等60位協同研發員工,通過創新主體的協同工作,不斷研發。以該企業作為案例,根據圖2復雜裝備協同研發績效評價指標,記錄并收集協同研發的工作數據,并通過式(12)計算每個指標數據的重要度,以臨界比率值來表示 (12) 式中,g表示績效評價指標,W(λ)表示研發引用的評價指標λ的指標合集,Z表示由g發出的指標總數,L表示評價權重系數。 經過上述過程,將收集到的數據作為實驗樣本,為了驗證所提方法的整體有效性,在Simulink仿真平臺中對所提方法進行測試,分別采用基于合作創新網絡的復雜裝備協同研發績效分析方法(方法1)、基于結構方程模型的績效分析方法(方法2)和基于文獻編碼的績效分析方法(方法3)進行測試。通過指標臨界比率值驗證評價指標的合理度,當臨界比率值不超過2時,表明評價指標沒有異常,不同方法的指標臨界比率值如圖3所示。 由圖3可知:在60次迭代中方法1選取的復雜裝備協同研發績效評價指標的臨界比率值均低于2.0;方法2和方法3選取的復雜裝備協同研發績效評價指標的臨界比率值均高于2.0。臨界比率值高于2.0表明指標存在異常,低于2.0表明指標沒有異常。通過上述分析可知,方法1選取的指標合理度較高,因為方法1通過復雜裝備協同研發績效機制模型選取評價指標,提高了指標的合理度。 將均方根誤差作為測試指標,進一步對上述方法進行測試,測試結果如圖4所示。 對圖4中的數據分析可知:方法1在多次迭代中獲得的均方誤差均低于0.2;方法2在多次迭代中獲得的均方誤差在0.5附近波動;方法3在多次迭代中獲得的均方誤差在0.6附近波動。對比不同方法的測試結果可知,方法1的復雜裝備協同研發績效評價結果的均方誤差較低,評價結果準確,根據評價結果得到的分析結果精準度越高,因為方法1利用合理度較高的評價指標對復雜裝備協同研發績效進行評價,提高了分析結果的精準度。 圖4 不同方法的均方誤差 在國民經濟中裝備制造業為企業各部門的發展和生產提供了所需的技術裝備,以維持部門的生存和擴張。當前復雜裝備協同研發績效分析方法存在指標合理度較低和分析精準度不理想等問題,因而提出基于合作創新網絡的復雜裝備協同研發績效分析方法,通過復雜裝備協同研發績效建模,選取評價指標,提高了評價指標的合理度,通過合理度較高的指標在MaxDEA軟件中對復雜裝備協同研發績效進行自動評價,合理度較高,均方誤差小于0.2,提高了分析結果的精準度。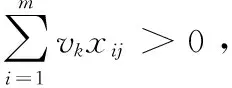
3 仿真實驗與結果分析
4 總結

