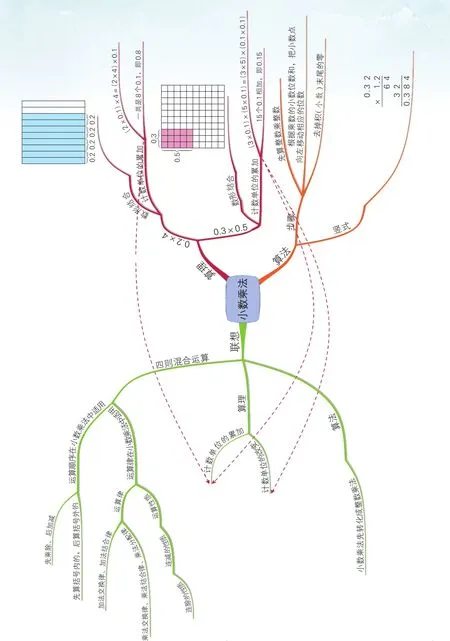
聯系整數乘法學習小數乘法

□孫敏洋

小朋友，小數乘法和整數乘法之間有什么關系呢？下面我們通過思維導圖來梳理一下吧！

請看思維導圖（見第14頁圖）第一分支，算理，也就是小數乘法計算的道理。

先看0.2×4，通過數形結合來理解它：把正方形的面積看作1，平均分成10份，其中的兩份就是0.2，根據乘法的意義可知0.2×4就是4個0.2相加，從圖中可以看出結果是0.8。

我們還可以把0.2×4變一變，寫成（2×0.1）×4，把括號去掉，再交換0.1和4的位置，就是（2×4）×0.1=8×0.1，一共是8個0.1，即0.8，這是從計數單位累加的角度解釋了0.2×4=0.8的計算道理。

再看0.3×0.5，通過數形結合來理解它：把大正方形的邊長看作1，它的面積就是1×1=1。把正方形的每條邊都平均分成10份，一條邊中的3份是0.3，另一條邊中的5份是0.5，0.3×0.5就是圖中涂粉色部分的面積。大正方形被平均分成了100個小正方形，每個小正方形的面積是0.01，涂粉色部分一共有15個小正方形，因此0.3×0.5的積是15個0.01，也就是0.15。

從計數單位累加的角度來理解 0.3×0.5，就是（3×0.1）×（5×0.1）=（3×5）×（0.1×0.1）=15×0.01，即 15個 0.01相加，和是0.15。

比較數形結合和計數單位的累加，你會發現這兩種方法其實是相通的，只不過數形結合可以讓你看得更直觀，理解起來更方便。

基于對算理的理解，我們來看思維導圖（見第14頁圖）第二分支，小數乘法的算法。

通過對算理的剖析，你會發現，可以先把小數乘法當成整數乘法來計算，計算出的積其實就是實際積的計數單位的個數，然后需要去確定實際積的計數單位是多少，你會發現這和乘數的小數位數有關。如整數乘一位小數，實際積的計數單位是0.1；一位小數乘一位小數，實際積的計數單位是0.01，即需要根據乘數的小數位數和，把算出來的結果的小數點向左移動相應的位數。如果實際積的末尾出現0，最后要去掉。如計算0.35×0.04，先算35×4=140，因為0.35是兩位小數，0.04也是兩位小數，所以要把140末尾隱藏的小數點向左移動4位，也就是0.0140，最后把小數末尾的0去掉，也就是0.014。

小數乘法和整數乘法一樣，也有豎式計算，需要注意的是，我們在計算小數乘法時是先把它當成整數乘法計算，因此小數乘法的豎式應末尾對齊，如第14頁圖中計算0.32×1.2的豎式。

小數乘法和整數乘法之間又有什么關系呢？請看思維導圖（見第14頁圖）第三分支。

顯然，它們的算法之間是有聯系的，我們需要把小數乘法先轉化成整數乘法計算。

其次，它們的算理之間也有聯系：從乘法的意義角度來說，乘法是加法的簡便運算，因此無論是整數乘法還是小數乘法，都可以看作計數單位的累加。需要注意的是，整數乘法和小數乘法都有可能導致計數單位的改變，如10×20，可以看作1個十乘2個十，積是2個百，用算式表示是 10×20=（1×10）×（2×10）=（1×2）×（10×10）=2×100。0.2×0.5=（2×0.1）×（5×0.1）=（2×5）×（0.1×0.1）=10×0.01，即2個0.1乘5個0.1，積是10個0.01。

再者，整數四則混合運算中的運算順序和運算律在小數四則混合運算中也是成立的：小數四則混合運算也是先算乘除，后算加減。先算括號內的，再算括號外的。加法交換律、結合律，乘法交換律、結合律和分配律，以及連減、連除的性質在小數四則混合運算中同樣適用。

小朋友，現在你對小數乘法的計算了解了嗎？