基于EMD 去噪的煤礦井下地質構造聲學探測技術
陳亞萍
(蘭州資源環境職業技術大學,甘肅 蘭州 730022)
從行業發展角度分析,地質構造一直制約煤礦生產發展的核心[1]。在近些年現代化技術不斷發展的大環境下,現代化礦井不僅大大提高了掘進速度[2],同時也使得地質構造在開采過程中受到的破壞程度日益加深[3]。面對這一發展現狀,以提前預知工作面發展狀況為基礎的地質構造探測工作就顯得尤為重要[4],其也是煤礦開采工作提前做好安全措施[5],快速安全通過危險地質區域的基礎之一[6]。關于煤礦井下地質構造的探測研究,文獻[7]提出了一種以槽波技術為基礎的異常體探測,并以陽泉礦區為目標展開了實際應用測試,探測結果取得了良好的效果,但是部分地質構造相對復雜,受地下水源等因素的干擾作用,其表現出了一定的不穩定性。文獻[8]將瞬變電磁法應用到煤層覆巖狀態的探測研究中,實現了對水源性特征的準確探測,但是對于地下整體地質構造的分析相對薄弱。聲學探測技術作為一種以介質反射特性為基礎的地質分析方法,不僅可以實現對復雜地質構成的準確獲取同時不受采空區邊界的限制,在煤礦井下地質構研究中具有巨大的應用潛力,但是聲波中的噪聲信息會影響最終的判斷結果。對此,提出基于EMD 去噪的煤礦井下地質構造聲學探測技術。
1 聲學探測信號去噪處理
1.1 聲波探測信號EMD 處理
為了實現對煤礦井下地質構造的準確探測,需要對采集到的聲波進行去噪處理[9],提高信號的可靠性。以此為基礎確保對構造的分析結果與實際結果之間的誤差降到最低。為了實現該目標,本文采用EMD(Empirical Mode Decomposition,經驗模態分解)方法實現對聲波信號的去噪。EMD 去噪的原理是首先對聲波探測信號進行小波變換,將其能量分布集中在較小的系數范圍內,該范圍對應聲波探測信號的小波系數表現出良好局部性的區間。同時需要注意的是,這些小波系數只有顯著地分布在各個分解尺度上時,最終才能實現對雜波的完整去噪。而地質環境構造中的噪聲經過小波變換后,系數分布同樣處于細尺度變換的小波域范圍內。通過調節分解尺度的大小即可實現對噪聲的完全去除。結合該去噪思路,本文利用EMD 對聲波探測信號去噪過程共分為3 個實施階段。
假設采集到的含噪聲的聲波探測信號為

其中,y 表示含噪聲的聲波探測信號,x 表示有效聲波探測信號,n 表示噪聲信號。
首先,對含噪聲波探測信號進行小波變換處理,并在該階段保留最大尺度范圍內的低通濾波的系數,需要注意的是,要確保小波系數與真實聲波探測信號的變換系數保持一致。針對該問題,本文利用非線性處理的方式對各個尺度下的高通濾波進行統一化處理,將此時得到的系數作為小波變換處理的系數,實現對聲波探測信號的轉換。對應的小波變換處理的系數計算方式可以表示為:

其中,λ 表示小波變換系數,λ(h)和λ(l)分別表示高通濾波下的波變換系數和低通濾波下的波變換系數,z表示可以執行的最大尺度范圍。
在此基礎上,利用EMD 根據設定閾值函數對聲波探測信號進行去噪處理。
由于煤礦井下地質構造的復雜性以及構成上的多樣性,使得礦井下巖體介質的成分、結構和密度等存在明顯差異,而這種差異就使得探測聲波的傳播速度、能量衰減及頻譜成分等也表現出對應的差異化特征。利用此,本文將小波變換處理的聲波探測信號表示為由多個不同方向上的向量分量構成的分解參數,此時的含噪聲的聲波探測信號可以表示為:
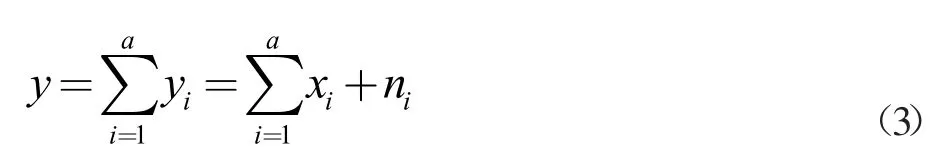
其中,yi,xi,ni分別表示分解后的含噪聲的聲波探測信號有效聲波探測信號和噪聲信號。a 表示分解方向數量。由于噪聲聲波探測信號n 是以正態分布的形式存在的,且不同yi對應ni互不相關,因此ni對應的方差為常量值。結合這一特征,對信號中噪聲的去噪處理就可以理解為是對ni的差異化約束。其可以表示為:

其中,W(y)i表示對分解后聲波探測信號的小波變換,W-(1y)i表示分解后聲波探測信號的小波逆變換運算,u 和分別表示分解后聲波探測信號的小波處理結果,Q表示非線性去噪函數,也是實現去噪的核心步驟。
通過式(4)可以看出,要實現對聲波探測信號噪聲的有效去除,主要依賴于閾值的確定效果。
1.2 閾值自適應設置
為了在聲波探測信號去噪過程中更好地保留聲波探測信號的有效信息,同時實現對噪聲的有效去除,本文建立了閾值函數,通過其計算出最優的閾值范圍。在1.1部分已經提到,小波系數需要適應不同尺度上的變換需求,這就意味著閾值也要兼顧不同尺度聲波信號的特征。以此為基礎,本文設計的閾值函數為

其中,p 表示閾值函數,m 表示尺度參數,通過調節m值的大小,計算出不同尺度條件下對應的閾值。利用式(5),結合聲波探測信號和噪聲在不同分解尺度上的能量分布特征,就可以實現對去噪目的。
對于細尺度上的閾值范圍,本文以偏硬閾值函數對其進行計算,將其計算結果代入到式(4)中,濾除信號中的大部分噪聲。對于寬尺度上的閾值范圍,本文以偏軟閾值函數對其進行計算,將其計算結果代入到式(4)中,濾除臨界區的噪聲信號。因此本文建立了以m 調節尺度為目標的數學模型,通過最優化m 值提高式(5)計算結果的自適應性,確保去噪效果的可靠性。具體的數學模型如下:

其中,mj表示m 的數學模型,En和Ej分別表示聲波探測信號的能量以及目標聲波探測信號能量。按照這樣的方式,計算出最優的m 值,并且需要注意的是,對目標聲波探測信號能量的設置要以實際礦區地質特征為基礎。此時閾值函數從硬到軟的變化就可以通過調整m 值由最佳目標聲波探測信號能量到允許目標聲波探測信號能量實現。
在此基礎上,將式(6)代入式(5)即可獲得各個尺度上對應的閾值函數,利用得到的結果作為EMD 去噪的基準,實現對聲波探測信號的過濾。
2 地質構造探測
在得到去噪后的地質聲波探測信號后,就可以根據其表現出的特征實現對區域相應構成的分析和判斷。
對煤礦井下地質進行探測所采用的聲學探測技術屬于主動聲納技術的范疇。通過聲納方程可將傳播介質、探測目標和探測設備的作用聯結在一起,利用聲納方程建立的關系,能夠實現對探測系統性的分析。實際應用中根據不同的系統模型可以建立不同的聲納方程式,對深地層而言,聲傳播損失和穿透的深度等指標就可以建立地層模型后,通過聲納方程進行大致估算。設置聲納方程式為:

式中,SL 為聲源級;Hd為煤礦井下深度(m);At為透射系數;α 為信號帶寬內煤礦井下的平均聲衰減(dB/B);RL為待測界面反射強度(dB);DT 為檢測閾;NL 為信號帶寬內平均噪聲譜(dB)。
對煤礦井下地質的聲波反射與透射產生影響的介質參數有粒徑、密度、孔隙度、聲速及衰減系數等。根據生源級及計算方程式右邊的各參數,可以求出傳播損失,進而估算出穿透地層的深度。
基于此分析在探測煤礦井下地質構造時,需要了解聲場特性。可以從應用的額角度建立信噪比模型,得出信噪比表達式,得到信噪比簡化模型,分析條件:
(1)各地層界面平行時,收發聲基陣的聲軸都垂直于地面,并具有良好的后輻射抑制能力;
(2)在工作頻段內聲波對各地層的穿透系數Ati和反射系數Ari為常數;
(3)輻射聲脈沖的幅頻特性如下式所示,其具有線性相應特性:

(4)接收濾波器的傳遞函數具有下式幅頻特性,且具有線性相位特性:
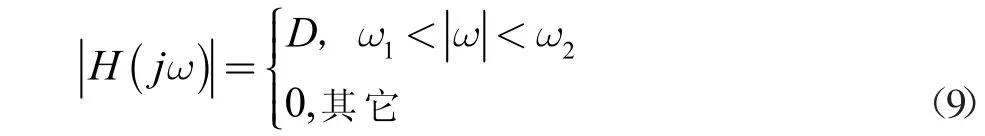
(5)接收聲基陣的聲電轉換函數K(jω)在工作頻段內為常數K0;
(6)不考慮延時;
(8)噪聲為各向同性、零均值的平穩高斯過程。
在上述環境下,從模型出發得出的最大信噪比的條件為:

式中,cw為聲速;S 為發射基陣面積,a 為噪聲系數;Ak為待測地面反射系數,HD為地層厚度,Ht為第i 層厚度,βi為第i 層吸收系數。
基于此計算出做基礎的地層構成。將聲波信號中的高頻能量作為各地層的分界,對各個高頻能量分量之間的聲波進行個性化分析,將其利于已有的巖體特征信號進行對比,擬合度越高,則表明其與對應的地質特征越相似,最后將相似度最高的巖體判定為該地層的巖體構成。
3 實例分析
為了測試本文設計地質構造探測技術的實際應用效果,進行了實際應用分析。
3.1 礦區地質背景介紹
本文進行實例分析具體的參數信息如表1 所示。

表1 測試區域基巖地層構成詳細信息
在此基礎上,對礦區的覆蓋層狀態進行統計,發現其主要構成為第四系沉積物,砂粘互生,并伴隨有卵礫層不連續發育,下伏地層與之有非密切接觸,且整體厚度變化較大,最厚位置可達到750m,最薄位置僅為230m。不僅如此,在測試區域內還伴隨有兩條明顯的斷裂,在區域構造應力的作用下,二者分別呈現出東西發展趨勢和東南發展趨勢。以此為基礎,采用本文方法對該區域的地質構造進行探測,并分析其探測結果與實際構成之間的一致性。
3.2 探測結果與分析
采用三種方法對地質構造的探測結果如表2 和表3所示。
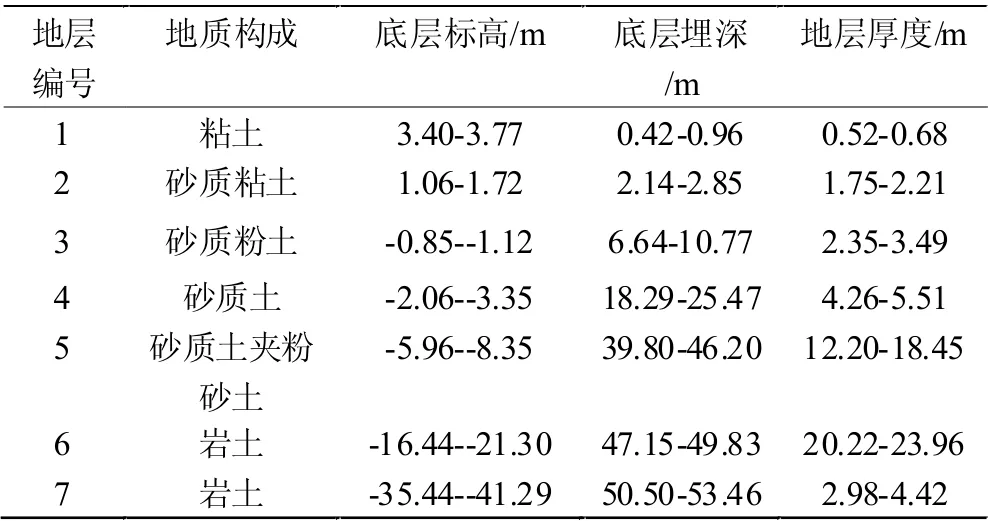
表2 礦區地質構造探測結果
從表2 和表3 中可以看出,本文設計的地質構造探測方法可以實現對地下巖體構成以及成分含量,相關屬性參數的獲取,對于實際的開采工作具有有效的指導價值。不僅如此,通過觀察表2 中的數據可以看出,其最大探測深度為地下53.46m,能夠滿足大多數礦區的探測需求,對于各地層信息位置以及厚度信息的探測精確到0.01m,可以為開采工作的開展提供可靠的數據支撐。
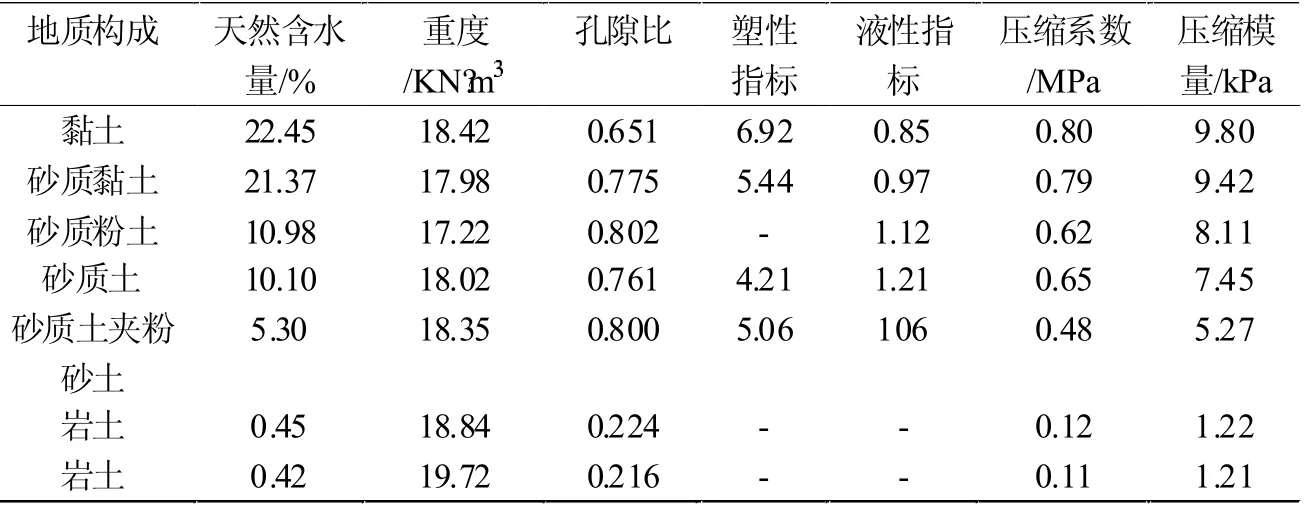
表3 地質構成分析結果
結束語
隨著礦產資源需求量的不斷增加,對其的探測和開采力度也逐漸增加。不僅如此,在礦井機械化程度不斷提高的背景下,如何切實有效地提高煤礦的安全性成為了備受關注的問題之一。除開采技術和開采施工因素外,另一個影響煤礦井下安全的關鍵因素就是煤礦本身的地質構造,一方面其決定著開采施工的方向,另一方面其也直接決定著相關支護結構的等級要求。本文提出基于EMD 去噪的煤礦井下地質構造聲學探測技術研究,實現了對礦區地下構造的準確分析,也希望為相關工作的開展帶去幫助。

