基于紋理特征的PVA纖維束攪拌分散均勻性研究

曹源文，夏 杰，廖 科，曾建民，程志豪

(1. 重慶交通大學 機電與車輛工程學院，重慶 400074； 2. 河南鄭州西繞城公路發展有限公司，河南 鄭州 450052；3. 云南省交通規劃設計研究院，云南 昆明 650299)

0 引 言

聚乙烯醇(PVA)纖維的氫氧碳基團與水泥基的氫氧基團能形成牢固的氫橋[1-4]。在水泥基中加入PVA纖維可有效地增強水泥基的抗裂性能，提高水泥基的壽命[5-8]。然而，PVA纖維是束狀形式的微米級材料，在水泥基中難以分散均勻，導致PVA纖維的優良性能在公路交通建設中難以顯現[9]。

筆者在水泥基中加入PVA纖維之前，對PVA纖維進行攪拌分散，以此達到在水泥基中提高PVA纖維的分散效果，增強水泥基強度。PVA纖維的束分散均勻性是將PVA纖維束狀形態分散為單絲網狀形態的程度。纖維分散效果評價方法對研究纖維分散均勻性是最重要的一部分。能快速、準確地評價PVA纖維束在水泥基中的分散效果對于實際工程中提高PVA纖維束分散均勻性具有較大參考和借鑒價值。

傳統纖維束分散評價一般是通過直接觀察纖維束的分散情況進行。景元琳[10]使用透明容器裝纖維混合液，直接觀察纖維束的分散情況；白光等[11]通過對實驗得到的混凝土性能進行測試，得到PVA纖維束對水泥基的強度影響情況；仇何等[12]根據測量分散后的分散系數等相關參數對分散效果進行評價。筆者利用數字圖像處理技術，采集PVA纖維束分散統計型紋理特征信息，采用灰度共生矩陣理論，分析評價了PVA纖維束和粉煤灰質量比、攪拌轉速及攪拌時間對PVA纖維束分散均勻性的影響，得到了最佳質量比、最佳轉速和攪拌時間。

1 統計型紋理特征

紋理是反映圖像中不受顏色、亮度變化影響的同質現象的視覺特征。紋理特征可表示圖像的灰度等級分布，紋理特征基本元素為：① 紋理基元，由像素組成具有一定色調、大小、形狀和區域屬性的連續集單元；② 紋理基元排列組合，通過紋理基元進行排列組合形成紋理。

統計型紋理特征能很好地表示圖像紋理的分布均勻性情況[13]。統計型紋理分析是指從區域統計方面來進行圖像紋理分析，通過圖像灰度空間分布情況對圖像紋理的粗細度、均勻性、方向性進行描述。筆者研究的是PVA纖維束分散后圖像，圖像中PVA纖維與混合物質的灰度值差異大，故統計型紋理特征能很好表示PVA纖維束的分散均勻性。

2 統計型紋理特征評價方法

統計型紋理特征根據像素及周圍的灰度信息，研究區域內的灰度統計特征。統計型紋理特征參數用灰度共生矩陣特征參數表達，灰度共生矩陣表示在某個方向上相隔d個像素的一對像元的灰度值分別是i和j的概率，這是計算估計圖像的二階組合條件概率密度方法，能很好表示圖像紋理的分布均勻性情況。

2.1 灰度共生矩陣理論

定義灰度等級為e1的點為原點，某像素點距離此點(Δx, Δy)的灰度等級為e2，坐標關系如圖1。

圖1 灰度共生矩陣點對的位置關系Fig. 1 The positional relationship of the point pairs of the graylevel co-occurrence matrix

(Δx, Δy)取不同值時，在不同方向上就可得到像素點對的灰度共生矩陣P(e1,e2,d,θ)，如式(1)：

(1)

(2)

式中：d為灰度共生矩陣的生成步長；θ為灰度共生矩陣的生成方向；N為灰度共生矩陣元素總數。

2.2 統計型紋理特征參數選取

灰度共生矩陣有很多的特征參數，其中，R.M.HARALICK[14]定義了14個特征參數來描述紋理特征。這14個參數中角二階矩反應了圖像分布均勻性，熵值反應了圖像紋理粗細和復雜程度。筆者選用角二階矩和熵值這兩個參數來進行PVA纖維分散的均勻性評價。

1)角二階矩計算如式(3)：

(3)

從式(3)中可看出：在圖像中紋理越粗，角二階矩f1的值更大，灰度分布更不均勻；相反，紋理越細，角二階矩f1值更小，灰度分布更均勻。

2)熵值f2(entropy)的計算如式(4)：

(4)

當圖像中沒有紋理時，矩陣P為零矩陣，熵值f2趨近零；當圖像中充滿了大量紋理，矩陣P(e1,e2,d,θ)中的數值幾乎相似，此時熵值f2最大；當圖像中有較少紋理時，矩陣P(e1,e2,d,θ)中元素數值差異較大，熵值f2較小。

2.3 圖像統計型紋理特征參數提取

PVA纖維通過分散試驗之后，對分散后的試驗樣品進行圖像提取，得到分散纖維的RGB圖像，利用MATLAB的圖像格式轉換程序將RGB彩色圖像轉化成灰度圖像。將灰度圖像利用灰度共生矩陣程序在MATLAB中計算，得到分散纖維角二階矩和熵值兩個特征參數[15]。采集流程如下：

1)將灰度圖像進行等級壓縮，將256級壓縮到16級；

2)取d=1，θ=0°、45°、90°、135°，在不同方向下計算出4個灰度共生矩陣；

3)將矩陣歸一化處理；

4)按照式(3)、式(4)，得到灰度圖像角二階矩和熵值；

5)在0°、45°、90°、135°這4個方向上進行計算，得到角二階矩和熵值，并對其進行平均化，得到統計型紋理特征參數。

2.4 PVA纖維束攪拌分散均勻性評價

筆者提取試驗后的PVA纖維圖像統計型紋理特征，用灰度共生矩陣中的角二階矩與熵值表示，用此特征參數來進行均勻性評價。在PVA纖維理想狀態的圖像中，圖像紋理越大，灰度分布越不均勻，角二階矩越大；圖像紋理越小，灰度分布越均勻，則角二階矩就越小。若灰度共生矩陣中數值都相同，則圖像熵值最大，紋理分布最復雜；若灰度共生矩陣中數值差異很大，則圖像熵值越小，紋理分布復雜程度越低。

因此，對分散后的PVA纖維束提取樣本，其角二階矩越小、熵值越大，即呈現單絲網狀結構圖像紋理越細小、分布越復雜，則PVA纖維分散均勻性效果越好。

3 PVA纖維束攪拌分散試驗及分析

3.1 攪拌分散裝置設計和材料選取

使用雙軸雙電機攪拌設備對PVA纖維束進行分散處理。攪拌裝置包括電機控制器、兩個電動機、兩個攪拌軸、聯軸器、攪拌葉片、攪拌槽，使用聯軸器將兩個電機的輸出軸分別和兩個攪拌軸連接。

將粉煤灰和PVA纖維束混合進行攪拌分散試驗。粉煤灰等級為二級，細度為43 μm，密度為2.4 g/cm3，含水量為0.5%；PVA纖維束長度為18 mm。圖2(a)為粉煤灰，圖2(b)為PVA纖維束。

圖2 粉煤灰和PVA纖維束Fig. 2 Fly ash and PVA fiber bundle

3.2 不同質量比對PVA纖維束分散效果試驗分析

在研究不同質量比對PVA纖維束分散效果影響時，選用4組不同的PVA纖維和粉煤灰比值，分別為：1∶15、1∶30、1∶45、1∶60。電機轉速為700 r/min，對纖維和粉煤灰攪拌時間為2 min。為保證試驗的準確性和防止設備、操作等誤差影響，每種質量比進行5次攪拌分散試驗，然后提取每次的角二階矩和熵值兩個紋理特征參數，并對5次試驗特征參數求平均值。圖3為試驗后不同質量比下的PVA纖維與粉煤灰混合示意。

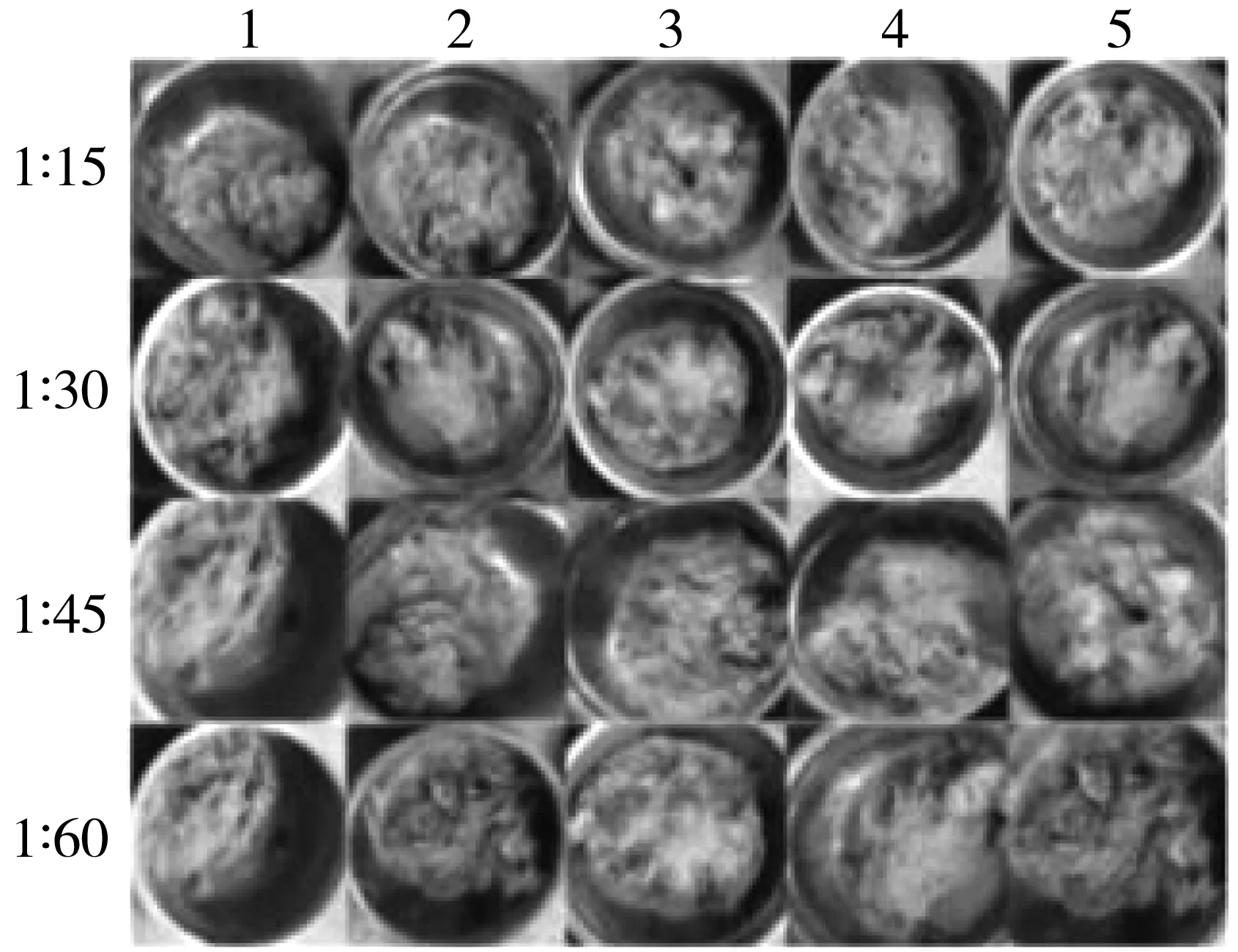
圖3 不同質量比下分散后的PVA纖維Fig. 3 PVA fiber dispersed at different mass ratios

攪拌分散試驗后，使用料篩將粉煤灰篩去，用水洗去PVA纖維上剩余的粉煤灰，圖4為水洗后的PVA纖維。

圖4 水洗后PVA纖維Fig. 4 PVA fiber after washing

采集水洗后的PVA纖維圖像，提取經處理后的圖像統計紋理特征參數，得到每次試驗的PVA纖維角二階矩與熵值；然后對每組質量比下得到的角二階矩與熵值求其平均值，將特征參數平均值作為評價PVA纖維束分散效果參數。

利用得到的PVA纖維角二階矩和熵值平均值繪制角二階矩隨質量比變化曲線和熵值隨質量比變化曲線，如圖5。

圖5 角二階矩和熵值分別與質量比關系曲線Fig. 5 Relationship curve between angular second-order moment, entropy and mass ratio respectively

從圖5可看出：PVA纖維中加入一定的粉煤灰，對PVA纖維束分散起著促進作用。圖5(a)中：隨著加入粉煤灰比例增加，分散后的PVA纖維圖像角二階矩越小，分散質量越好，當纖維束和粉煤灰比值增加到1∶45之后，圖像角二階矩變化不明顯，對提升纖維束分散質量不明顯。圖5(b)中：隨著加入粉煤灰比例增加，分散后的PVA纖維圖像熵值更大，分散質量越好，當纖維束和粉煤灰比值增加到1∶45之后，熵值變化很小，對于提升纖維束的分散質量影響不大。

3.3 不同轉速對PVA纖維分散效果試驗分析

在轉速對PVA纖維分散質量的影響試驗中，纖維束和粉煤灰質量比為1∶45時進行試驗。當轉速為300～900 r/min時，進行了7種轉速工況的試驗，每種轉速工況相差100 r/min，攪拌時間為2 min，每組試驗使用5 g PVA纖維。

試驗得到不同轉速下攪拌分散后PVA纖維的角二階矩和熵值平均值，并繪制角二階矩隨轉速變化曲線和熵值隨著轉速變化曲線，如圖6。

由圖6可看出：提高裝置轉速，對PVA纖維束分散起著促進作用。圖6(a)中：隨著轉速增加，分散后的PVA纖維圖像角二階矩越小，分散質量越好，隨著轉速達到700 r/min后，圖像角二階矩變化不明顯，對提升纖維束分散質量不明顯。圖6(b)中：隨著轉速增加，分散后的PVA纖維圖像熵值更大，分散質量越好，當轉速達到700 r/min后，熵值變化很小，對提升纖維束分散質量影響很小。

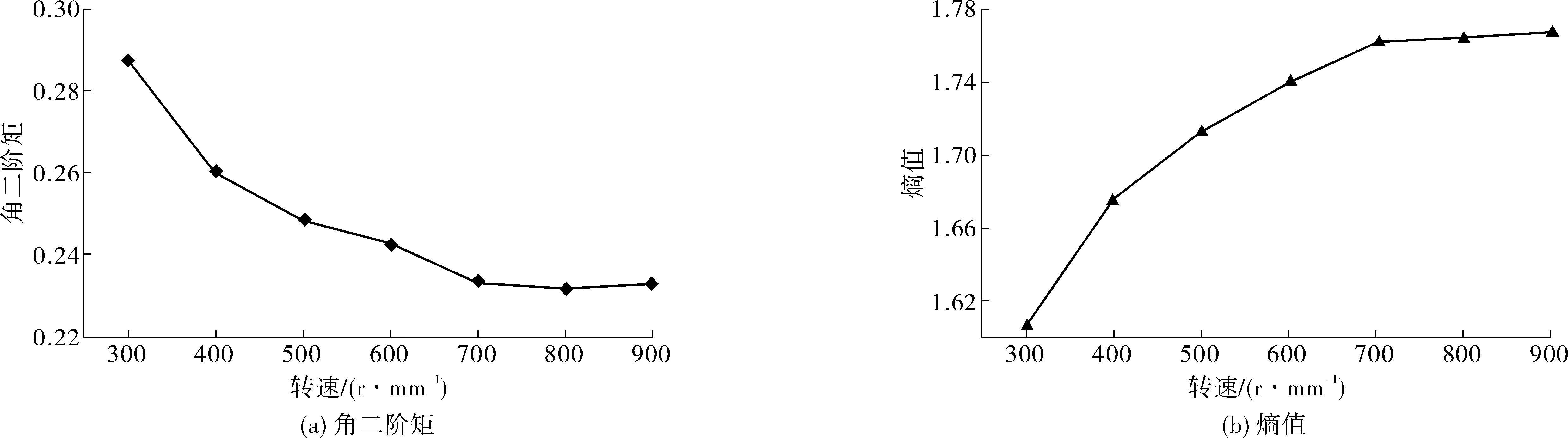
圖6 角二階矩和熵值分別與轉速關系曲線Fig. 6 Relationship curve between angular second-order moment, entropy and speed respectively

3.4 不同攪拌時間對PVA纖維分散效果試驗分析

在攪拌時間對PVA纖維分散質量影響試驗中，纖維束和粉煤灰質量比為1∶45，轉速為700 r/min時進行試驗。攪拌時間為2～4 min，進行了5種不同攪拌時間試驗，每次攪拌時間相隔0.5 min，每組試驗使用5 gPVA纖維。

試驗得到不同攪拌時間下的PVA纖維角二階矩與熵值平均值，繪制角二階矩隨攪拌時間變化曲線和熵值隨著攪拌時間變化曲線，如圖7。

從圖7可看出：增加試驗攪拌時間，對PVA纖維束分散起著促進作用。圖7(a)中：隨著攪拌時間增加，分散后的PVA纖維圖像角二階矩越小，分散質量越好，隨著攪拌時間增加到3 min后，圖像角二階矩變化不明顯，說明繼續增加攪拌時間對提升纖維束分散質量不明顯。圖7(b)中：隨著攪拌時間增加，分散后的PVA纖維圖像熵值更大，分散質量越好，當攪拌時間達到3 min后，熵值變化很小，甚至有下降趨勢，對提升纖維束分散質量影響不大。

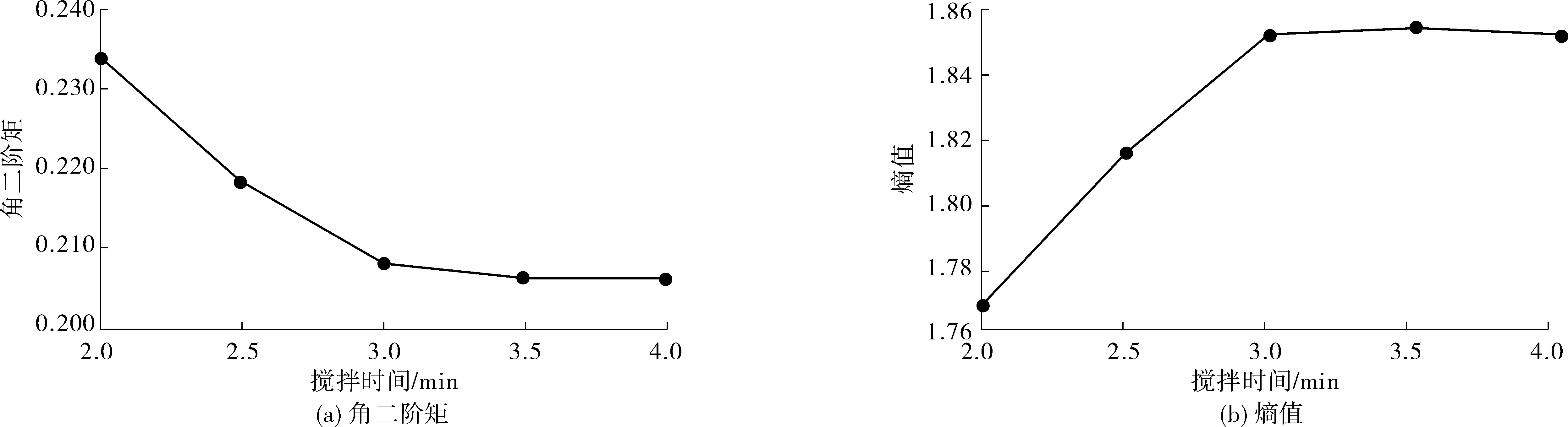
圖7 角二階矩和熵值分別與攪拌時間關系曲線Fig. 7 Relationship curve between angular second-order moment, entropy and stirring time respectively

4 結 論

1)筆者采用數字圖像紋理處理技術，對攪拌分散試驗后的PVA纖維束提取圖像進行處理，利用灰度共生矩陣理論提取圖像的統計型紋理特征參數：角二階矩和熵值，以此表征圖像紋理均勻性分布情況，實現對攪拌分散后的PVA纖維束進行均勻性評價。該方法能快速、準確地評價纖維束攪拌分散均勻性情況。

2)筆者開展了在不同PVA纖維束與粉煤灰質量比、不同轉速和不同攪拌時間下的PVA纖維束攪拌分散試驗。結果表明：粉煤灰加入比例越高，分散效果越好，但PVA纖維和粉煤灰質量比達到1∶45后，繼續添加粉煤灰，改善分散效果不明顯；提高轉速，能改善PVA纖維分散效果，但轉速達到700 r/min后，繼續提升轉速，對分散效果沒有促進作用，甚至降低PVA纖維束分散效果；增加攪拌時間，能改善PVA纖維分散效果，但攪拌時間在3 min后，增加攪拌時長對PVA纖維分散效果提升不大。試驗表明：最佳質量比為1∶45，最合適轉速為700 r/min，最佳攪拌時間為3 min。