多層有砟軌道結構彈性波波動行為及帶隙特性
張鑫浩,趙才友,張孝娟
(1.西南交通大學 唐山研究生院, 河北 唐山063000; 2. 西南交通大學 高速鐵路線路工程教育部重點實驗室,成都610031; 3.西南交通大學 土木工程學院,成都610031)
交通強國,鐵路先行。近二十年來,鐵路軌道在我國得到了持續快速發展,運營線路、總里程以及投入總金額等均穩居世界前列。與此同時,隨著中國鐵路交通線網不斷加密,列車速度不斷提高,由之誘發的振動與噪聲問題愈發嚴重,越來越引起人們的注意,振動和噪聲已被列為七大環境公害之一[1]。軌道結構的振動與噪聲輻射的本質原因可歸結于結構中的彈性波波動效應[2]。已有研究表明周期結構或聲子晶體具備特殊的力學特性,使得彈性波在某些頻段無法傳播,通常將上述頻率段稱之為“帶隙”或“禁帶”[3]。現代鐵路軌道通常被設計成一些具有重復且相同的結構單元,因此可參照聲子晶體或周期結構的思路進行研究。
迄今為止,針對周期結構的理論研究正在不斷開展。Brilliouin對鏈式周期結構中彈性波的波動進行研究,為周期結構的研究建立了理論基礎[4]。Mead根據波動方程研究了周期性梁、板結構的振動特性,證實了周期約束的梁、板結構中的彈性波也存在帶隙特性,并提出了空間諧波法、傳遞矩陣法等帶隙計算方法[5]。Heckl 對質量彈簧系統的不同支承方式進行討論分析,并研究了周期性支承Timoshenko梁中縱波、扭轉波、彎曲波的耦合振動特性[6]。
在對周期結構的工程實踐問題的研究中,Yu等采用傳遞矩陣法計算了周期性輸流管道中彎曲波傳播特性[7]。Yu 等根據城市軌道交通噪聲頻譜特性,通過引入周期結構帶隙理論,提出了一維氣-固周期型隔聲聲屏障結構[8]。馮青松等通過有限元法計算了歐拉梁中溫度力對帶隙的影響,但模型過于單一[9]。王平、易強等計算了單層點支撐、雙層點支撐軌道模型中的帶隙特性,研究了扣件剛度的影響,并從功率流的角度闡釋了帶隙特性,但并未考慮更為復雜的軌下基礎以及相應的波動模式[10-12]。此外上述研究多采用傳遞矩陣法(Transfer-Matrix Method簡稱TMM),僅能適用于一維周期結構,且對于復雜結構,傳遞矩陣法會出現矩陣病態甚至無法求解的問題,由此本文將聲子晶體研究方法中適用性更為廣泛的平面波展開法(Plane Wave Expansion 簡稱PWE)引入軌道周期結構的帶隙計算中,以期應用于計算復雜軌道結構以及二維、三維頻散曲線。總之,周期性軌道結構彈性波傳播的研究取得了很大的進展,但更為細致的工作和技術革新還有待于進一步深入的研究。
1 多層有砟軌道模型與波動方程
基于平面波展開法的基本原理,將有砟軌道以離散點支撐模型進行建模,見圖1,取軌枕間距l內的鋼軌及其軌下各支撐部件為一基本元胞,根據Bloch 定理及Floquet 變換,求解無限周期結構的頻散特性[13]。
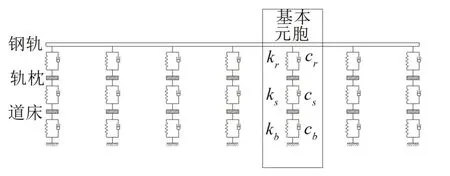
圖1 多層有砟軌道結構及基本元胞模型
在頻率波數域中的鋼軌位移解為:
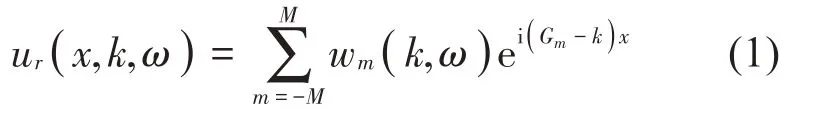
軌枕和道床的位移解為:
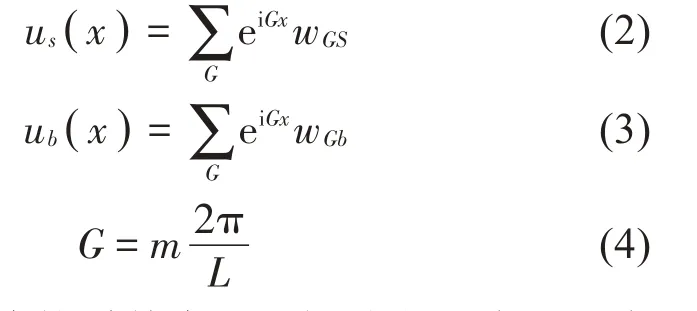
建立多層有砟軌道基本元胞振動方程式(5)、式(6)、式(7),將式(1)至式(4)代入振動方程式(5)、式(6)、式(7),可得頻率波數域下的頻散方程式(8)、式(9)、式(10):
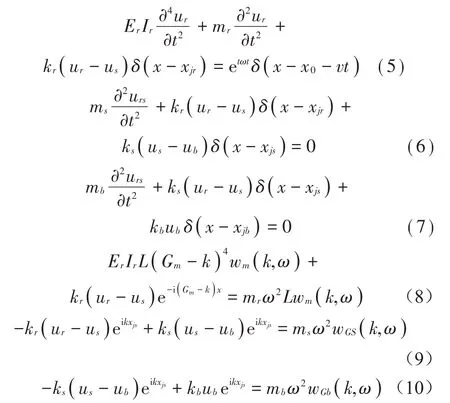
其中:k是限制在一維Brillouin區的波矢,wGm是一維倒格矢G對應的傅里葉系數。kr為扣件支撐剛度,ks為軌枕支撐剛度,kb為道床支撐剛度,Ir為鋼軌截面慣性矩,mr為單位長度鋼軌質量,ms為軌枕質量,mb為道床參振質量,Er為鋼軌彈性模量。
Gm取遍整個倒格矢,而實際計算中為所得到的該問題近似數值解,將鋼軌平面波數設置為n,總倒格矢數則有m=2n+1 個,則上述方程可化簡為經典平面波展開矩陣形式:

式中:P、Q均為(2m+1+2)階方陣,α為(2m+1+2)階列陣,從第一布里淵區選取波數k,即可得到軌道結構的能帶結構。
2 頻散曲線與帶隙
本文鋼軌平面波數取為41,既可以充分保證解的收斂,又不會使計算繁瑣。多層有砟軌道結構的相關參數如表1所示。

表1 有砟軌道結構參數表
利用上述方法可以得到多層有砟軌道結構頻散曲線,如圖2 所示,在0~57.4 Hz、72.14 Hz~122.2 Hz、141.9 Hz~243.5 Hz、1 454 Hz~1 490 Hz 出現帶隙特征,且與采用傳統的傳遞矩陣法計算得到的帶隙范圍相一致。
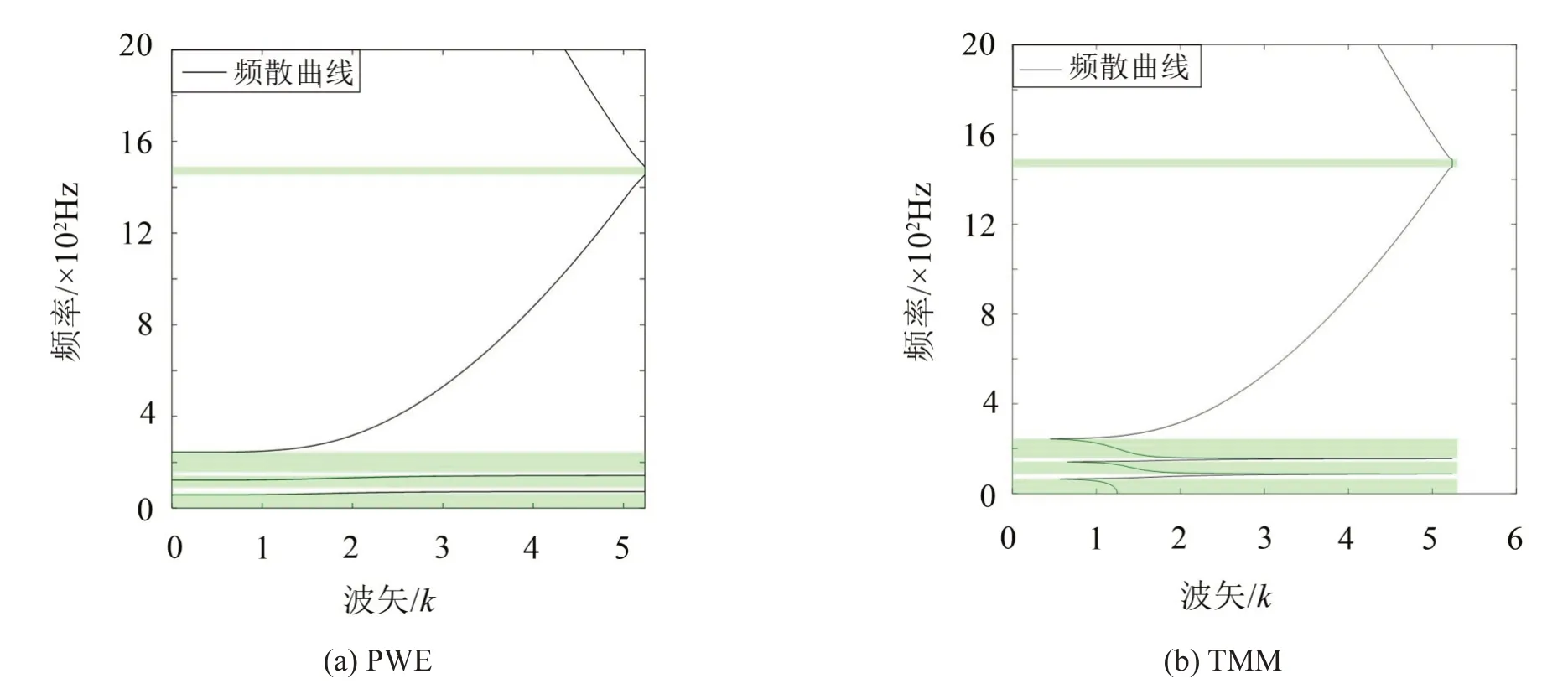
圖2 頻散曲線及帶隙圖
3 軌道參數的帶隙影響規律
多層有砟軌道結構各部件的參數直接影響帶隙特征,如圖3所示,隨著扣件支撐剛度增加,1階帶隙帶寬增大,2階帶隙帶寬不變,并向高頻移動,3階、4階帶隙的帶寬增大并向高頻移動;隨著軌枕支撐剛度增加,1 階、2 階帶隙帶寬增大,3 階帶隙帶寬減小并向高頻移動,4階帶隙保持不變;隨著道床支撐剛度增加,1 階帶隙截止頻率增大,2 階帶隙向高頻移動,但帶寬不變,3階帶隙起始頻率增大,4階帶隙保持不變;隨著元胞尺寸增大,1、2、3階帶隙帶寬均逐漸減小,而4階帶隙帶寬不變,并向低頻移動。根據上述規律,可以通過調控扣件、軌枕、道床的支撐剛度以及元胞間距等參數,實現對軌道結構彈性波傳播的控制。
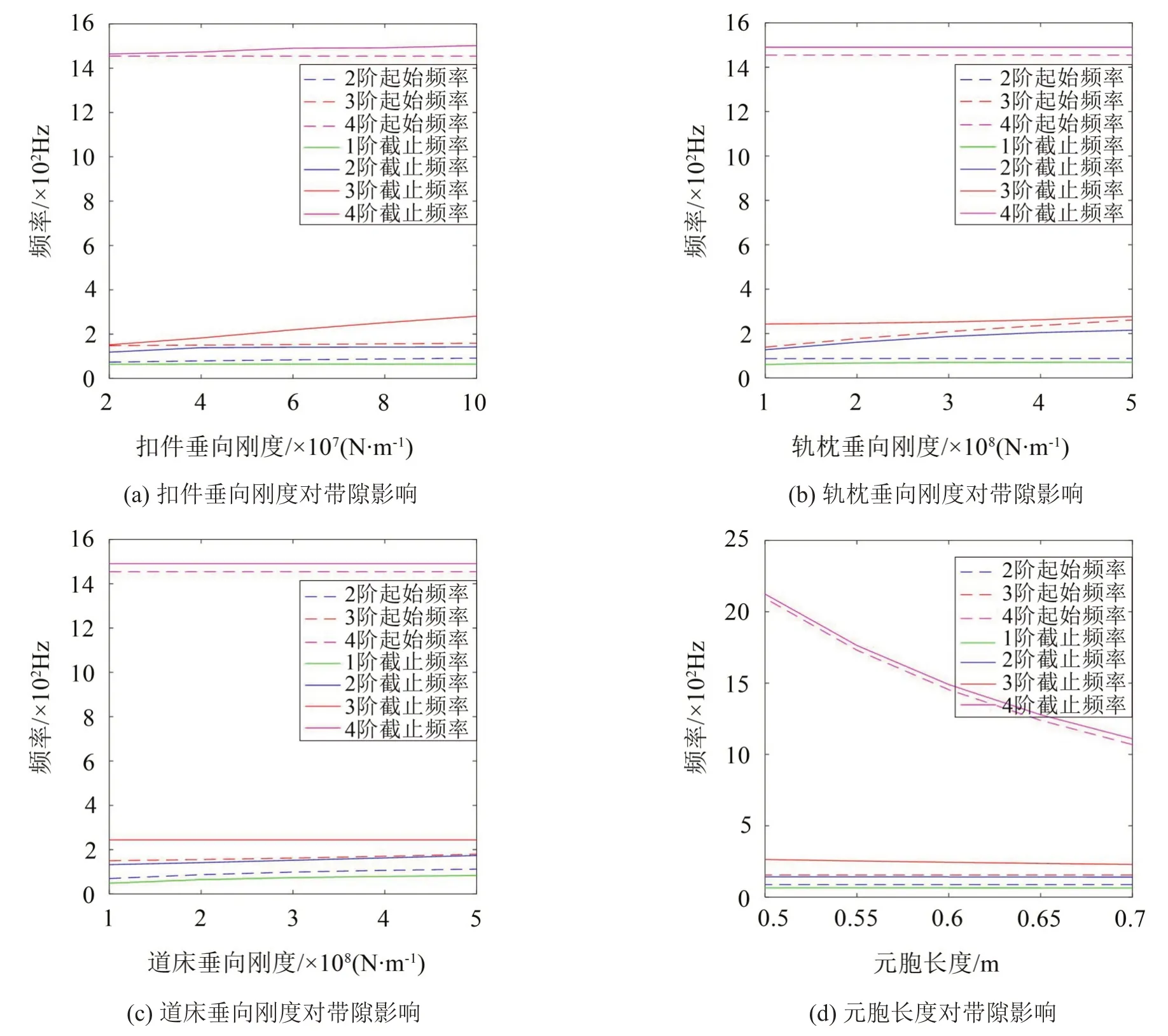
圖3 軌道結構參數對帶隙的影響
4 帶隙機理及帶隙邊界模式
現有研究表明,局域共振模型中依然存在Bragg帶隙,當周期結構的基本元胞長度為a時,Bragg 帶隙表征為元胞尺寸為半波長的整數倍,即:
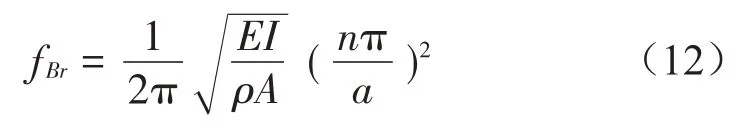
經驗算可知,第4 階帶隙(1 454 Hz~1 490 Hz)為Bragg 帶隙,且符合上述公式計算結果。在多層有砟軌道結構中,還存在局域共振帶隙,采用集中質量模型來描述帶隙的邊界模式。令:
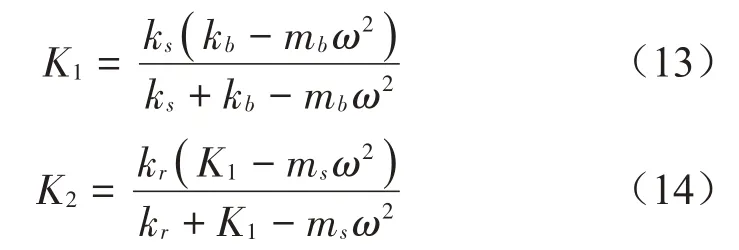
其中帶隙起始頻率模式滿足式(15):
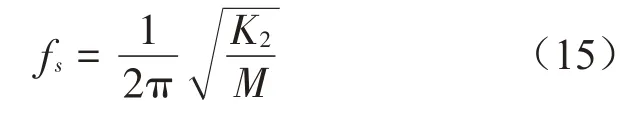
考慮到M>>m,即要求解:
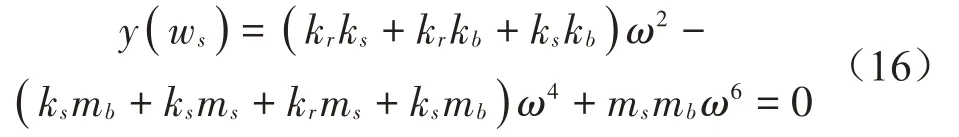
且

帶隙截止頻率模式滿足公式:
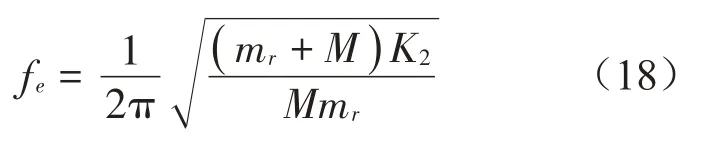
考慮到M>>m,即要求解:
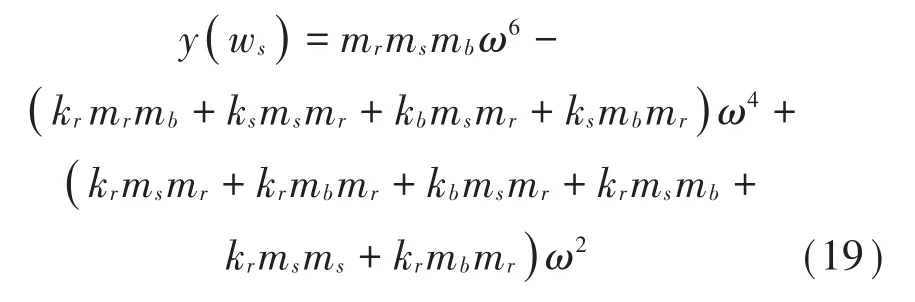
且

其中,起始頻率3 個正解對應的振動模式如圖4 所示,截止頻率3 個正解對應的振動模式如圖5 所示,其中實線代表初始位置,虛線代表變形后位置。
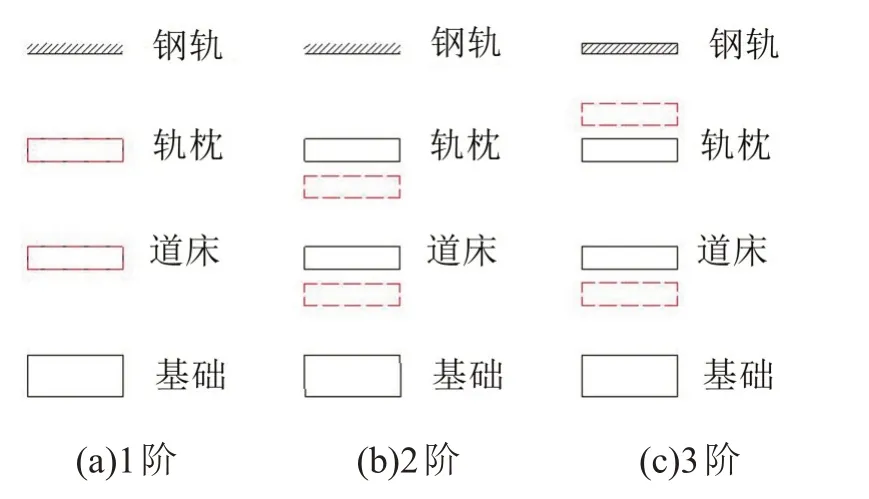
圖4 帶隙起始頻率振動模式
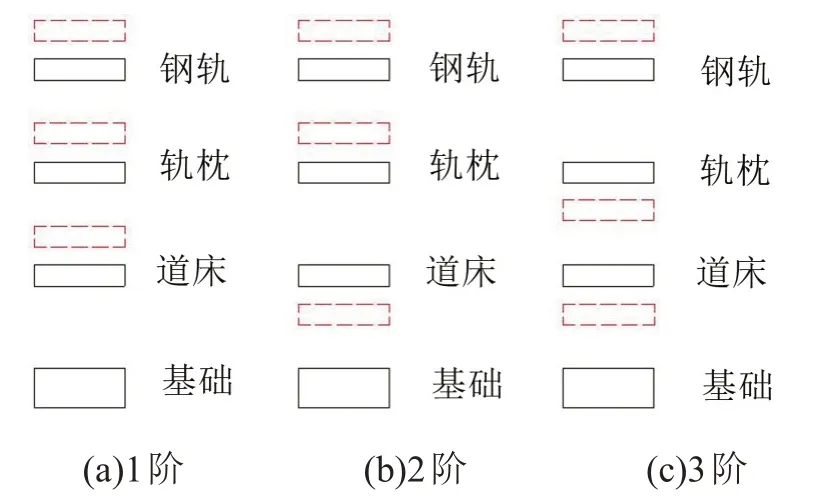
圖5 帶隙截止頻率振動模式
5 有限周期結構振動傳遞系數
為驗證多層有砟軌道結構的帶隙特性,分別建立5 周期與10 周期有限周期結構模型,計算單位簡諧荷載下不同位置處的鋼軌響應。激勵點位置響應為u0,第n跨處的鋼軌響應點響應為un,鋼軌振動傳遞系數為:
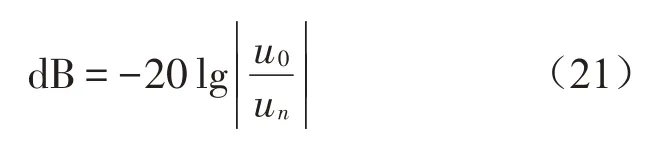
通過上述方法得到振動傳遞曲線如圖6 所示,可以看出傳遞曲線在(0~130 Hz)頻段內傳遞率均小于0,且最大衰減率達52 dB,彈性波無法傳遞,即存在帶隙特性。同理,在(72 Hz,122.4 Hz)、(142 Hz,245 Hz)存在明顯帶隙,且最大衰減率分別達到150 dB 和125 dB。而對于頻散曲線中的第四階帶隙頻段,由于其帶寬窄且衰減率較低,故傳遞曲線中的帶隙特征并不明顯。除上述頻段外,在其余頻率范圍內傳遞系數均大于0,振動無衰減,即為通帶。根據平面波展開法計算所得的帶隙特征,與根據振動傳遞規律所得結果完全吻合。因此,驗證了帶隙的存在以及計算的正確性。
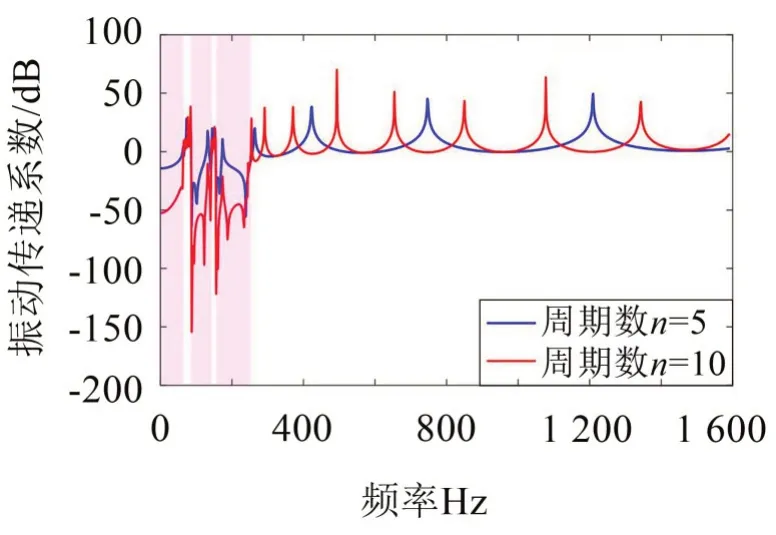
圖6 有限周期振動傳遞系數
6 通帶與帶隙范圍內彈性波傳播特性
為進一步分析多層有砟軌道結構中彈性波傳播特性以及帶隙對鋼軌及環境振動的影響,建立20個有限周期的元胞結構,在元胞左端位置處施加單位簡諧荷載,分別提取位于帶隙范圍內的60 Hz、90 Hz、200 Hz 以及位于通帶范圍內的70 Hz、150 Hz 、2 000 Hz的鋼軌及道床位移分布。
如圖7至圖12所示,對于帶隙范圍內的頻率,鋼軌及道床位移會沿著彈性波的波動方向快速衰減,表現出帶隙特性。此外,不同帶隙范圍內,衰減速度各不相同:60 Hz 位于第1 階帶隙內,彈性波傳遞至第13個元胞時,完全衰減;90 Hz位于第2階帶隙內,彈性波傳遞至第6個元胞時,完全衰減;200 Hz位于第3階帶隙內,彈性波傳遞至第10個元胞時,達到完全衰減。這符合上文中所計算的振動傳遞系數的大小關系。對于通帶范圍內的頻率,鋼軌及道床位移沿著彈性波的波動方向無明顯變化或衰減,即表現出通帶特性。
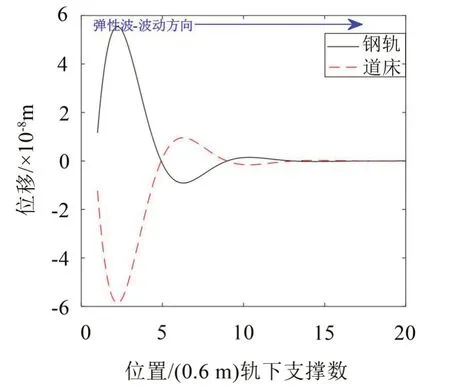
圖7 60 Hz(1階帶隙內)鋼軌及道床位移分布
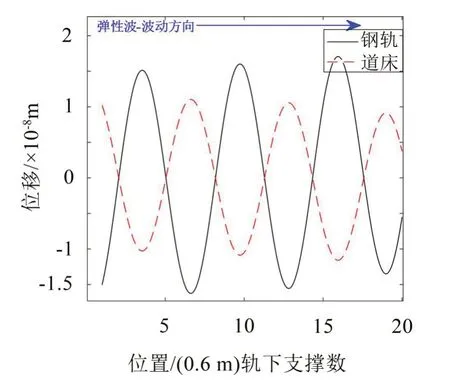
圖8 70 Hz(通帶內)鋼軌及道床位移分布
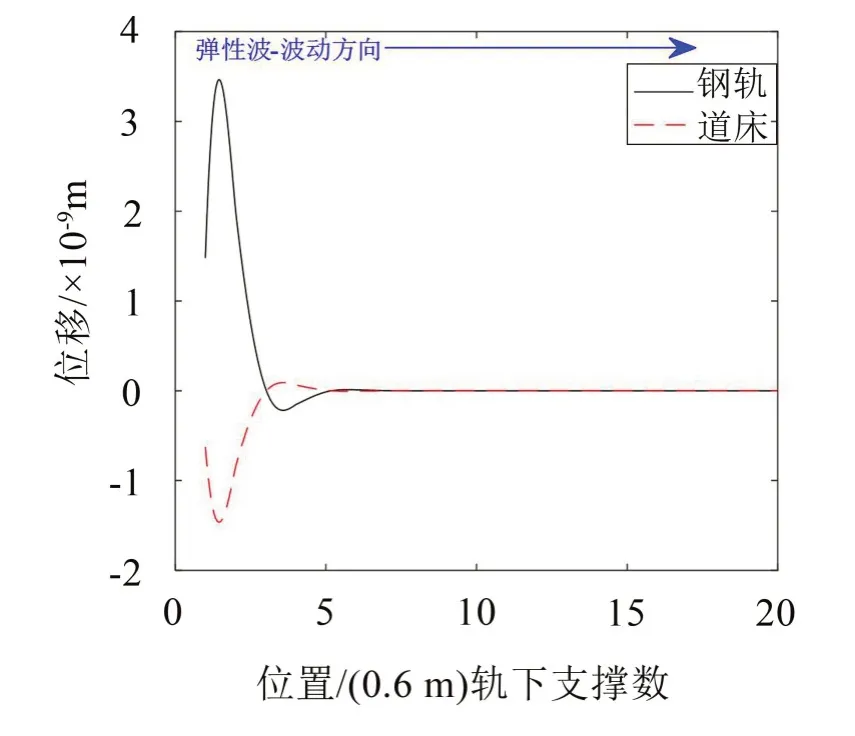
圖9 90 Hz(2階帶隙內)鋼軌及道床位移分布
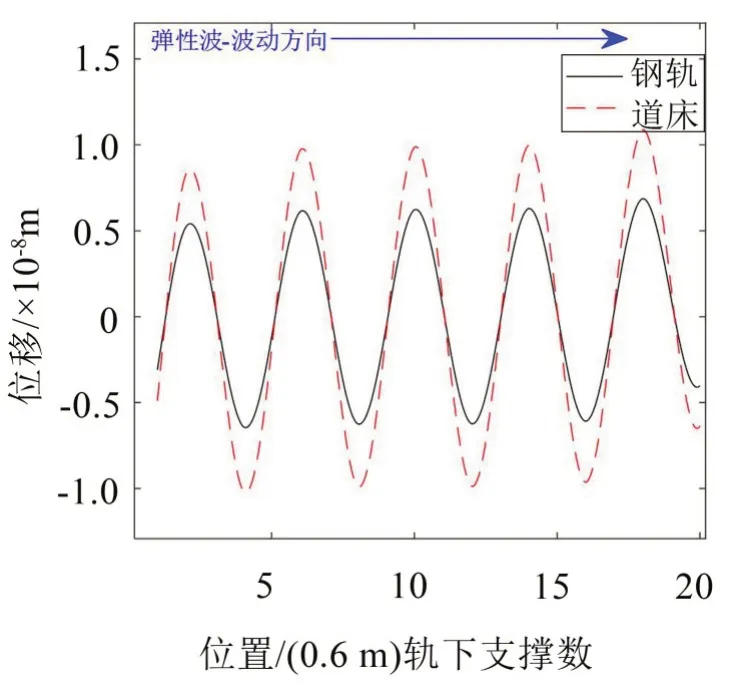
圖10 150 Hz(通帶內)鋼軌及道床位移分布
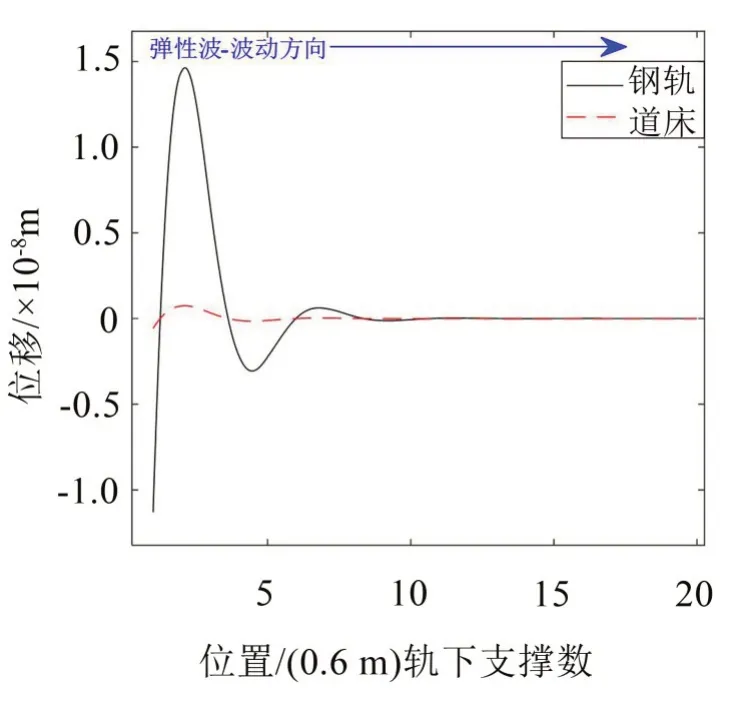
圖11 200 Hz(3階帶隙內)鋼軌及道床位移分布
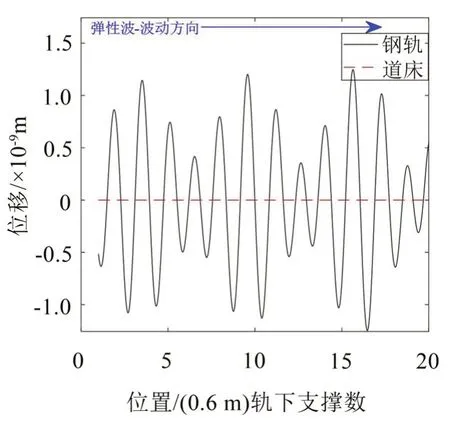
圖12 2 000 Hz(通帶內)鋼軌及道床位移分布
由此進一步證明有砟軌道結構的帶隙特性,以及帶隙的出現可有效抑制彈性波在環境中的傳播擴散。這為抑制軌道結構中環境振動、減少噪聲污染提供了新的思路和理論支撐。
7 結語
(1)本文基于平面波展開法,建立多層有砟軌道結構基本元胞波動方程,得出無限周期結構的各階帶隙為:0~57.4 Hz、72.14 Hz~122.2 Hz、141.9 Hz~243.5 Hz、1 454 Hz~1 490 Hz。
(2)多層有砟軌道結構中存在局域共振帶隙和Bragg 帶隙,局域共振帶隙主要受到扣件剛度、軌枕剛度、道床剛度等軌下支撐的影響;Bragg 帶隙主要受到扣件剛度及元胞長度的影響。垂向彎曲波局域共振帶隙的產生機理及振動模式可用彈簧振子模型進行描述,并分別給出了帶隙邊界解的方程;Bragg帶隙則由Bragg散射機理控制。
(3)求解有限周期數的多層有砟軌道結構振動傳遞系數,得到在各階帶隙范圍內彈性波沿軌道方向的傳播明顯衰減,即dB值小于0,從而驗證了帶隙的存在及計算的正確性。
(4)對于帶隙范圍內的頻率,鋼軌及道床位移會沿著彈性波的波動方向快速衰減,表現出帶隙特性,此外衰減速度與振動傳遞系數大小相符;而對于通帶范圍內的頻率,鋼軌及道床位移沿著彈性波的波動方向無明顯變化或衰減,即表現出通帶特性。由此表明了帶隙對鋼軌及環境振動具有抑制作用。

