面向差分隱私的BIRCH算法研究
王豪石,張淑芬,董燕靈,李帥
(1.華北理工大學理學院,河北唐山 063210;2.河北省數據科學與應用重點實驗室,河北唐山 063210;3.唐山市數據科學重點實驗室,河北唐山 063210)
0 引言
大數據時代,數據信息呈爆炸式增長,這些數據包含了生活的方方面面,例如,瀏覽器瀏覽的歷史數據、用戶瀏覽淘寶和京東等電商網站數據、手機客戶端上的登錄數據和使用數據、用戶的社交網站數據等。這些數據直接或者間接地涉及了用戶隱私信息,使得很多企業可以利用數據挖掘技術挖掘出用戶的喜好和生活習慣,以獲得巨大的利益。對于用戶而言,這可能會造成個人隱私泄露。如果這些數據被一些不法之人惡意利用,可能會給用戶帶來難以預料的人身傷害和財產安全。此外,用戶的一些不正規操作也可能導致用戶信息泄露。因此,如何保護用戶隱私成為當前亟待解決的問題。
隨著數據泄露事件頻發,隱私保護技術越來越受到學術界的重視。目前,已有針對敏感數據的隱私保護方法可分為:數據失真、抑制發布及數據加密。其中,數據失真是通過加入擾動實現隱私保護;抑制發布是根據真實情況對數據進行有條件的發布;數據加密是采用加密技術對數據集中的敏感數據進行加密處理。在數據挖掘中,聚類分析是根據研究對象的特征進行分類,但在其聚類分析中經常會出現隱私泄露問題,如何保護數據隱私安全逐漸成為研究的焦點。對此,彭春春等針對數據可用性與隱私保護性,利用本地化差分隱私方法在本地進入隨機擾亂,之后在K-modes算法的初始中心點上將出現次數最多的數據作為初始中心點,提出支持本地化差分隱私保護的K_modes聚類方法;蔡英等使用針對混合型數據,利用Laplace機制對數值型添加噪聲,用指數機制對分類型數據加噪,提出基于K-prototype聚類的差分隱私混合數據發布算法;傅彥銘等對K-means++算法在選取初始化中心點和迭代中心點中存在的隱私泄露問題,提出一種基于拉普拉斯機制的差分隱私保護K-means++聚類算法研究。
在BIRCH算法構建聚類特征樹時存在聚類特征隱私泄露現象,故本文提出面向差分隱私的BIRCH算法。在BIRCH算法構造聚類特征樹的聚類特征SS與LS中添加拉普拉斯噪聲,以實現保護聚類特征的隱私安全。實驗結果表明,本文提出的DPBIRCH算法能在保證聚類結果準確性的情況下,添加不同的隨機噪聲,實現不同級別的數據隱私保護效果。
1 相關技術
1.1 差分隱私
定義1
差分隱私。假設隨機算法B
滿足ε
-差分隱私保護,則對任意相鄰的兩個集合D
和D
以及P
的任意子集S
,滿足如下條件: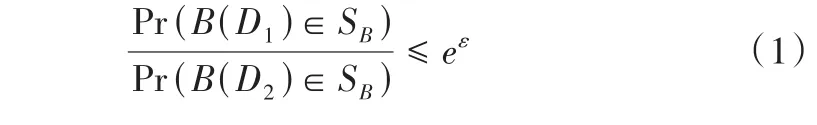
ε
是使用者的指定常數,Pr(.)為概率密度函數,D
和D
為兩個只差一條數據的相鄰數據集,P
是B
所有的輸出集合。從數學的角度看,只要參數ε
足夠小,攻擊者是很難從相差為1的數據集D
和D
中經過分析發現用戶的一些真實信息。定義2
全局敏感度。Δf
是查詢函數f
的敏感度,定義為: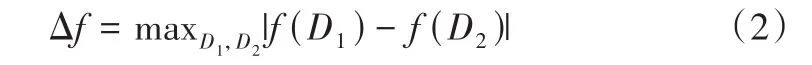
其中,D和D是具有相同結構的數據集,且至多相差一個元素。
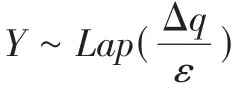
q
與隱私預算參數ε
決定。Δq
越大,添加的噪聲越大,Δq
越小,添加的噪聲越小,添加噪聲的值跟Δq
成正比;反觀ε
值的情況,ε
越大添加的噪聲越小,ε
越小添加的噪聲越大,添加噪聲的值與ε
的值成反比。從不同參數的拉普拉斯的噪聲分布圖(見圖1)可以看出其與ε
的值成反比。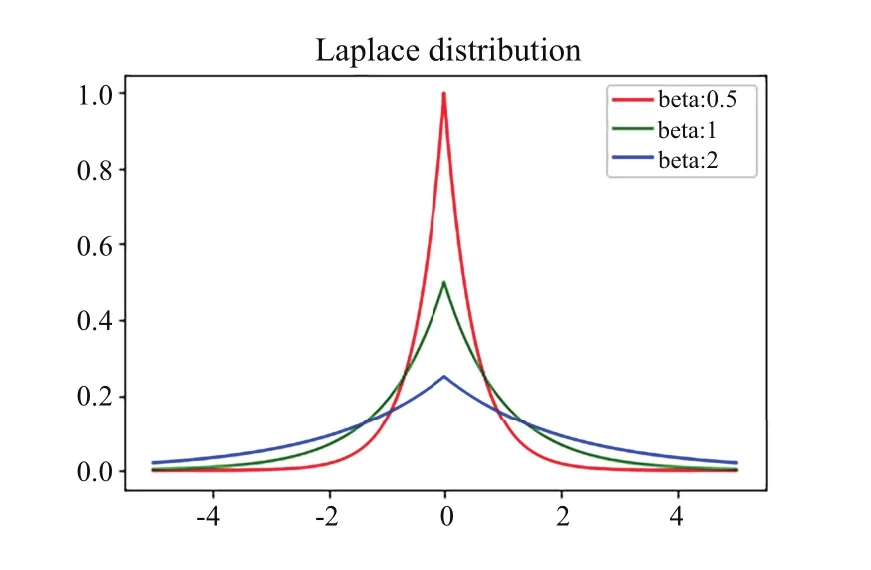
Fig.1 Laplace noise mechanism圖1 拉普拉斯噪聲機制
1.2 層次聚類
聚類是根據數據特征將一個數據集劃分為不同的子集或者簇的過程,聚類算法包括基于劃分的聚類、基于層次的聚類、基于密度的聚類。BIRCH算法(Balanced Iterative Reducingand Clustering Using Hierarchies)是常見的層次聚類算法之一,主要思想是用三元組表示一個簇點的相關信息。其算法基本流程為:①遍歷數據集,根據初始化的閾值,建立起初始聚類特征樹;②修改閾值,將滿足新閾值條件的簇構造成一棵新樹,并判斷所有節點是否滿足修改后的閾值,對大于閾值條件的進行分裂,并根據就近原則加入所屬的特征樹中。重復步驟②,直到一棵完整的樹凝聚完成。
2 面向差分隱私保護的BIRCH算法
2.1 BIRCH算法
BIRCH算法利用聚類特征樹(Clustering Feature Tree,簡稱CFTree)實現聚類,其聚類特征樹類似于平衡B+樹。
聚類特征(Clustering
Feature
,CF)是一個包括簇信息的三元組(N,LS,SS),其中N代表樣本點的個數;LS代表所有樣本點的線性和,SS代表所有樣本點的平方和。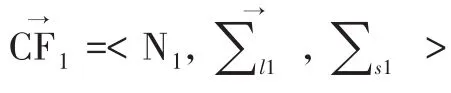
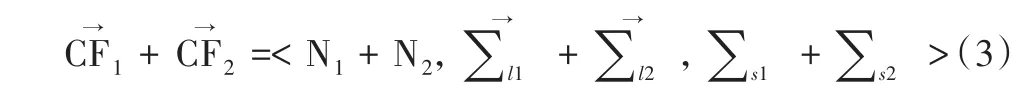
可加性定理表明,每個父節點的三元組的值是其所有子節點三元組值之和,這一性質使得在更新CF Tree時算法效率更加高效。
2.2 DPBIRCH算法
本文針對在構造CF Tree中存在的CF隱私泄露現象,提出了面向差分隱私的BIRCH算法(DPBIRC算法)。在BIRCH算法構造CF Tree的CF中的LS與SS中加入拉普拉斯噪聲,最終達到保護CF的隱私信息和數據的作用。在DPBIRCH聚類算法流程中最關鍵的步驟是在建立聚類特征樹中加入拉普拉斯噪聲,其噪聲添加過程如下:
步驟1:新數據添加后,檢查CF所對應的球體半徑閾值,當閾值小于T,則更新路徑上所有CF的三元組,并且在LS與SS中添加拉普拉斯噪聲,到此,插入結束,轉入步驟3;
步驟2:當前葉子節點上CF的個數小于葉子節點最大CF的個數,這時創建一個新的CF,放入新數據,將新的CF節點放入這個葉子節點,更新路徑上所有的CF三元組,并在LS與SS中添加拉普拉斯噪聲,此時,插入結束。
DPBIRCH算法流程具體如下。
算法1:DPBIRCH算法

上述算法中,枝平衡因子B是指父節點中子節點的最大數目;葉平衡因子L是指葉子節點中CF的最大數目;閾值T是指葉子節點子聚類的最大直徑。
2.3 隱私性分析
在拉普拉斯機制中,如果算法中的隨機函數能夠滿足拉普拉斯的分布噪聲,就能夠實現對數據的隱私保護。DPBIRCH通過在BIRCH算法中的聚類特征SS與LS添加噪聲,實現差分隱私保護。本文設定兩個拉普拉斯機制函數,其隱私預算都為ε
,其中一個對SS添加噪聲,另一個對LS添加噪聲。證明:算法1中的第8、13與9、14滿足差分隱私。
假設D
和D
是任意相鄰數據集,B
是加噪算法,LS加噪后為LS,根據拉普拉斯機制: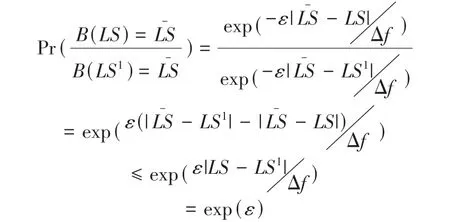
同理可證SS的加噪過程為:
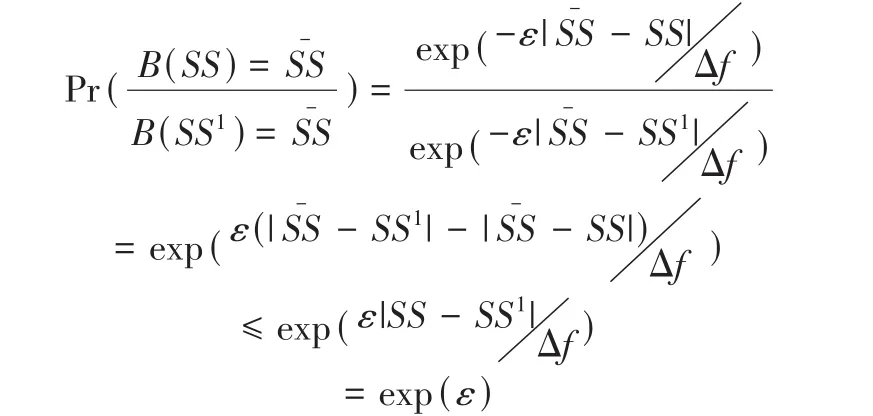
ε
,LS中加噪消耗隱私預算的值等于總的隱私預算ε
;根據差分隱私的串行組合原理,DPBIRCH算法消耗總的隱私預算為2ε
。2.4 DPBIRCH算法評價指標
面向差分隱私的BIRCH算法可以從兩個指標進行分析,分別為差分隱私保護強度和聚類的準確性。
(1)差分隱私保護強度。差分隱私下的保護強度受隱私保護預算參數ε
的影響,當隱私保護預算參數ε
的值越小,添加的拉普拉斯噪聲就越大,差分隱私保護強度越高;反之,當隱私保護的預算參數ε
值越大,添加的拉普拉斯噪聲就越小,差分隱私保護強度越低。(2)聚類準確性。RI指標(Rand Index),簡稱蘭德系數,是一種用排列組合的方式對聚類進行評價,用于比較各聚類算法的準確性。本文將其用于比較添加噪聲后數據聚類結果與原始數據聚類結果的相似度,如式(4)所示。

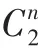
ARI指標(Adjusted Rand Index)簡稱調整蘭德指數。ARI解決了RI不能很好地描述隨機分配簇標記向量相似度的問題。ARI的定義如式(5)所示。
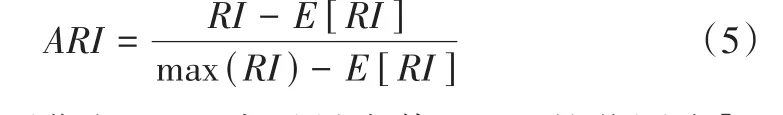
E
表示期望,max表示最大值。ARI
的范圍為[-1,1],ARI
的值越大表示不同簇之間的相似度越高,ARI的值接近于0表示隨機分配簇,ARI
的值為負數表示預測的簇向量非常差。本文算法通過設置不同的隱私預算參數ε
,比較原始的數據聚類結果與添加拉普拉斯噪聲后的數據聚類結果,計算出ARI指標與RI指標的值,從而在保證聚類準確性的同時實現數據隱私保護。3 實驗結果與分析
3.1 實驗設計
本文實驗采用Python語言實現面向差分隱私的BIRCH算法。實驗平臺內存為16GB,操作系統為Win10系 統,CPU為Intel core i5-9300H 2.40GHz,顯卡為GTX16504G GDDR5,Python語言的版本為3.8.3,開發工具為Pycharm 2020.2.3,實驗所用的數據集是從UCI數據集上下載的MAGICGamma Telescope數據集(MAGIC伽瑪望遠鏡數據集)。其實驗數據集基本信息如表1所示。

Table1 Basic information of experimental data set表1 實驗數據集基本信息
為了驗證DPBIRCH算法的隱私保護性,本文實驗在不同隱私保護預算參數的值與簇值情況下,通過比較原始數據聚類結果與添加拉普拉斯噪聲后的數據聚類結果,計算出RI指標與ARI指標的值,并觀察RI指標與ARI指標值的變化情況。
具體操作如下:首先,設置不同的簇值,通過添加相同的拉普拉斯噪聲觀察原始數據聚類結果與添加拉普拉斯噪聲后數據聚類結果的RI指標和ARI指標值變化情況;其次,設置簇值相同時,通過添加不同的拉普拉斯噪聲觀察原始數據聚類結果與添加拉普拉斯噪聲后數據聚類結果的RI指標與ARI指標值變化情況。其中,隱私保護預算參數ε
的取值分別為0.01、0.05、0.1、0.2、0.4、0.8,簇的取值分別為2、3、4、5,交替進行對比實驗,并觀察取10次聚類結果平均值后的RI指標與ARI指標值變化情況。由于對數據集作了歸一化處理,且范圍為[0,1]區間,故根據敏感度的定義可知Δq
的值為1。3.2 實驗結果與分析
針對在UCI數據集上的MAGICGamma Telescope數據集,使用本文面向差分隱私的BIRCH算法對該數據集在進行BIRCH算法時設置不同簇值以及不同隱私保護預算參數ε
的值進行對比實驗,觀察原始數據聚類結果與添加拉普拉斯噪聲后數據聚類結果的RI指標與ARI指標值的情況,并統計與分析所得的RI指標和ARI指標值變化情況。取10次聚類結果平均值后的RI指標與ARI指標值的情況如表2、表3所示。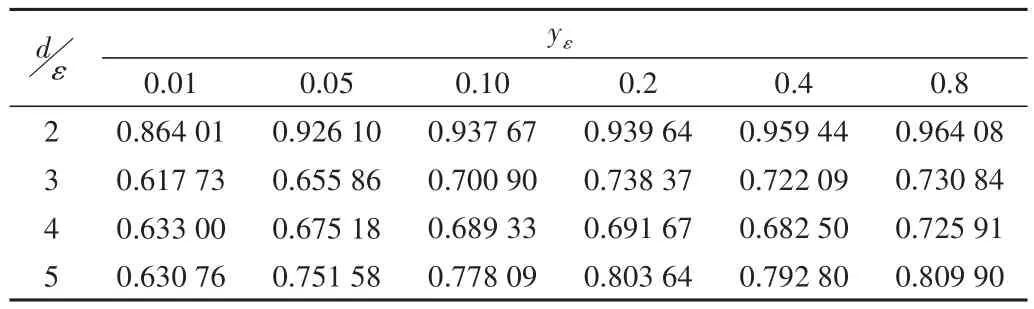
Table2 MAGIC Gamma Telescope RIindica tor values on the dataset表2 MAGIC Gamma Telescope數據集上的RI指標值情況
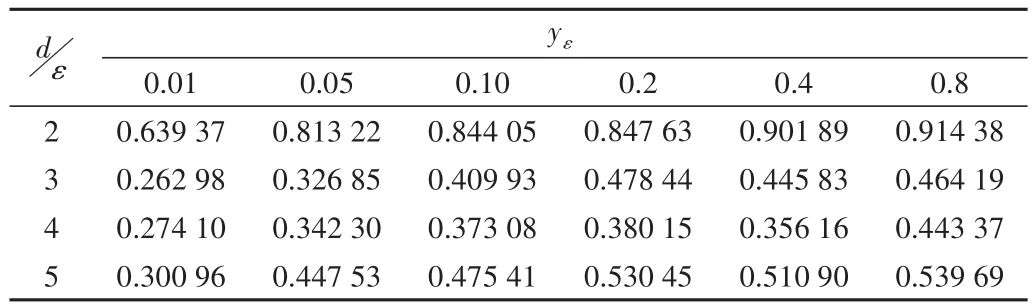
Table 3 MAGIC Gamma Telescope ARI index values on the dataset表3 MAGIC Gamma Telescope數據集上的ARI指標值的情況
表2、圖2為在MAGICGamma Telescope數據集上隱私保護預算參數ε
的值和簇值對應的RI指標值變化情況;表3、圖3為在MAGICGamma Telescope數據集上隱私保護預算參數ε
的值和簇值對應的ARI指標值變化情況。從圖2、圖3可以看出,整體上RI指標與ARI指標的值都隨著隱私保護參數預算ε
值的增大而增大。其中,在比較原始的數據聚類結果與添加拉普拉斯噪聲后的數據結果而計算出的RI指標與ARI指標的情況看,當簇值為2的情況下得到AI指標與ARI指標的值最大,且聚類效果最佳。其對應RI指標的值為0.864 01、0.926 10、0.937 67、0.939 64、0.959 44、0.964 08;ARI指標的值為0.639 37、0.813 22、0.844 05、0.847 63、0.901 89、0.914 38。根據實驗結果分析可知,在MAGICGamma Telescope數據集中添加不同的拉普拉斯噪聲,會對數據產生不同的隱私保護級別。總體上,當差分隱私的隱私保護預算參數ε
值越大,RI指標與ARI指標受到的影響越小,數據隱私的保護級別越小,可用性就越大,聚類所得到的RI指標與ARI指標的值越接近1;相反,當差分隱私的隱私保護預算參數ε
值越小,RI指標與ARI指標受到的影響就越大,數據隱私的保護級別越大,可用性就越小,聚類所得到的RI指標與ARI指標的值也越小。在確保聚類準確性的前提下,為實現對數據的隱私保護,本文在利用DPBIRCH算法時,對于ε
的取值有一定要求,ε
的取值不能太小,否則影響到數據集的可用性與聚類的準確性;同時ε
的取值也不能太大,否則會起不到保護數據隱私的作用。由本文實驗可知,在MAGIC Gamma Telescope 數據集上,當ε
的值等于0.2 時,RI 與ARI 指標同ε
小于0.2 時相比增長明顯;且大于0.2時,RI 指標與ARI 指標同ε
等于0.2 時增長緩慢。故ε
的值大于等于0.2 時,聚類結果的準確率相比ε
小于0.2 時提高明顯,同時也保護了數據隱私安全。
Fig.2 Relationship between RI index and differential privacy budget parameter ε value on MAGIC Gamma Telescope dataset圖2 MAGIC Gamma Telescope數據集上的RI指標與差分隱私預算參數ε值之間的關系
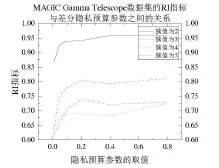
Fig.3 Relationship between ARI index and differential privacy budget parameter ε value on MAGIC Gamma Telescope dataset圖3 MAGIC Gamma Telescope數據集上的ARI指標與差分隱私預算參數ε值之間的關系
4 結語
基于傳統的BIRCH 算法在進行聚類構建CF Tree 時會存在CF 隱私泄露現象,為了保護BIRCH 算法中CF 的隱私安全,本文提出了面向差分隱私的BIRCH 算法,通過設置不同的隱私預算參數,對構建聚類特征樹的聚類特征LS與SS 中添加噪聲,以驗證不同隱私預算參數下聚類結果的準確性與可用性。下一步將研究如何更加高效準確地對數據添加噪聲,以及差分隱私保護在其他機器學習算法中的適用性。

