改進小波閾值法在電力線載波通信降噪中的應用
吳穎穎,鐘建偉,李禎維,吳建軍,李家俊
(1.湖北民族大學 信息工程學院,湖北 恩施 445000;2.國網湖北省電力有限恩施供電公司,湖北 恩施 445000)
0 引 言
要實現電力系統各環節互聯互通,普及電網全面態勢感知,需要以電力物聯網通信作為支撐,充分應用各類先進通信技術,形成具有信息處理高效、應用靈活等特征的智慧服務系統。然而,隨著大量智能傳感設備的接入,系統中無疑會出現各類具有不同通信需求的業務,同時必然會引起數據量爆發式增長,對現有通信方式提出了嚴峻挑戰。
低壓電力線載波通信(Low Voltage Power Line Communication, LVPLC)以電力線為傳輸介質進行數據傳輸,與無線通信相比具有不受天氣及遮蔽物影響的特點,天然具有電氣設備互聯、建設成本低等優勢,是電力物聯網信息交互的有效通信方式之一。電力線載波通信技術由傳統窄帶電力線載波通信(Narrow Power Line Communication,NPLC)逐漸發展成寬帶電力線載波通信(High Power Line Communication, HPLC),在帶寬容量、傳輸速率和穩定性方面都有了極大提升。然而,與無線局域網接入及光纖寬帶等其他傳統通信方式相比,以電力線作為傳輸信道也使載波信號易受用電環境影響,在一定程度上降低了LVPLC的可靠性。如何在接機處選擇合適的噪聲處理方案,是降低載波信號受電力網噪聲影響、提升系統傳輸可靠性與準確性的關鍵。
目前流行的載波通信降噪方案主要包括單載波調制技術、擴頻技術、正交頻分復用技術(Orthogonal Frequency Division Multiplexing, OFDM)及降噪算法等。單載波調制技術需要配合偵測技術、均衡技術等輔助技術,擴頻技術犧牲帶寬以提高抗干擾能力,采用OFDM技術仍會一定程度上受到用電環境的干擾。因此,研究有效的噪聲消除算法尤為必要。文獻[5]運用獨立分量分析原理并結合基于負熵的FASTICA算法實現對載波信號的去噪,但效果有限;文獻[6]提出了小波變換結合高階累積量盲分離算法對載波信號進行檢測,但噪聲模型過于理想化;文獻[7]提出了一種小波去噪結合雙譜分析的方法,能夠準確辨別不同干擾因素,但載波模型與低壓電力線有一定差異;文獻[8]提出了一種考慮碼元信號的時頻混合降噪算法,但應用場景有限。
本文針對低壓電力線載波噪聲進行分析建模,研究小波變換理論并提出一種改進的小波閾值函數,通過改變可調參數并對比不同參數下的去噪效果,利用小波變換對電力線載波通信信號進行降噪處理。經仿真實驗分析,驗證了該方法的有效性。
1 低壓電力線載波噪聲分析
影響電力線載波通信傳輸質量的重要因素是電力系統中來源廣泛、時變性強的各類噪聲。在低壓電力線通信信道中,噪聲主要分為5類:有色背景噪聲、窄帶噪聲、工頻同步噪聲、工頻異步噪聲以及隨機脈沖噪聲。
1.1 有色背景噪聲
有色背景噪聲廣泛分布于整個頻譜,是一種以小型電器為代表的低功率電氣設備產生的噪聲,通常采用AR模型對其進行描述,n階自回歸AR模型傳遞函數為:

式中:A(z)為輸入函數;a為濾波器系數;n表示階數。
1.2 窄帶噪聲
窄帶噪聲的頻帶較窄,通常由中、短廣播信號與電力線信號串擾產生,其數學模型可表示為n個獨立的正弦函數的疊加:

式中:A為噪聲幅值;f為噪聲中心頻率;φ為初相位。
1.3 工頻同步噪聲
工頻同步噪聲是一種主要由中大功率電氣設備中的硅控整流器在工頻周期內進行一定次數的通斷時產生的噪聲,其頻率為50 Hz或100 Hz,其數學模型可視為有色背景噪聲與周期矩形脈沖的乘積:

式中:n(t)為有色背景噪聲;r(t)為周期矩形信號。
1.4 工頻異步噪聲
工頻異步噪聲來源廣泛,通常由帶顯示功能的電子設備產生,其數學模型可表示為:

式中:l為脈沖個數;A為脈沖幅值;f為周期脈沖頻率;t為單個脈沖出現的時間;φ為初相角。
1.5 隨機脈沖噪聲
隨機脈沖噪聲通常由電氣設備在開斷瞬間產生,或雷電瞬間干擾也會產生,持續時間都在微秒級,其數學模型可表示為:

式中:τ與脈沖寬度有關,一般取脈沖寬度的五分之一;t表示脈沖的到達時間。
分析低壓電力線載波不同噪聲的數學模型,可以看出電力線載波通信噪聲具有周期性、突發性、連續性、隨機性及時變性。
2 小波閾值去噪法
2.1 小波變換基本原理
小波變換是對時間頻率的局部化分析,它與傅里葉變換相比,增加了時窗的概念,改變尺度因子和平移因子對信號進行伸縮平移,就可以自動適應時頻分析的要求,在高頻處細分時間,在低頻處細分頻率,實現對信號的多分辨分析。
小波閾值去噪的具體步驟如下:
(1)選擇合適的小波基,根據公式計算分解層數,對含噪信號y(t)進行離散小波變換,得到由低頻至高頻的各層小波細節系數d;


小波閾值去噪流程如圖1所示。

圖1 小波閾值去噪流程
2.2 小波閾值去噪的改進方法
2.2.1 小波閾值選取
閾值是區分有效信息與噪聲的邊界,閾值選取過大會導致有效信息與噪聲一起被濾除;閾值選取過小則不能充分濾除噪聲。傳統的通用閾值對各尺度下的小波細節系數閾值使用固定閾值,但由于噪聲的小波系數隨尺度增加而減小,使用固定閾值自適應能力差,去噪效果不佳。
含噪信號經小波變換處理后,大部分噪聲都存在第一層細節系數中,在此基礎上,D.L.Donoho等人將第一層小波細節系數的噪聲方差作為整體噪聲方差,提出了小波去噪的通用閾值估計方法,但閾值恒定不變僅適合第一層分解系數。本文根據噪聲隨機分布在各層小波系數的特性,逐層估計各層噪聲的均方差,最終計算出不同尺度下的閾值:

式中,σ為第j層小波系數均方差,可通過式(7)計算:

由式(7)可知,j=1時,ln(j+1)<1,小波閾值增大,利于第一層噪聲消除;>1時,ln(+1)>1,隨著的增大,后續尺度下閾值減小,符合噪聲分布的一般規律。
2.2.2 改進閾值函數
傳統的小波閾值函數包括軟閾值函數和硬閾值函數。
設閾值≥0,硬閾值函數定義如下:

軟閾值函數的定義如下:

分析軟、硬閾值函數的數學特性,兩種方法均有一定缺陷。硬閾值法保留大于閾值的小波細節系數,將小于閾值的系數直接置零,函數在處間斷,將導致重構信號產生振蕩;軟閾值函數雖然能夠解決連續性問題,但會使重構信號與真實信號間產生恒定偏差。同時,兩種方法皆是將絕對值小于閾值的系數直接取零,將混疊在噪聲頻譜中的有效信號徹底濾除,也會影響重構信號與原始信號的逼近程度。
本文提出一種改進小波閾值函數:

式中,,為調節因子,且>0,≥1。
當d→λ時,

同理,該函數在-λ處連續,本文的改進函數在(-∞,+∞)內連續,解決了硬閾值函數在閾值處不連續的問題。
當d→∞時,

隨著小波細節系數的增加,直至d→∞時,本文的改進函數在數學形式上無限趨近于硬閾值函數,降低了軟閾值函數所造成的恒定偏差。
改進閾值函數曲線如圖2所示。

圖2 改進閾值函數曲線
2.3 小波基與分解層數
小波變換的實質是用小波基函數逼近原始信號的過程,應用小波分析對電力線通信信道噪聲信號進行去噪時,為抑制噪聲干擾并準確提取原信號信息,要求選用的小波基具有緊支撐正交性、對稱性、精確重構性等。
在對電力線通信信道噪聲進行降噪之前,首先需要選擇恰當的分解尺度,正確劃分信號頻帶。分解尺度過小會導致去噪結果不理想,分解尺度過大會導致去噪后有效信息大量丟失。要限制基頻對其他子頻帶產生影響,可以使基頻處于最低子頻帶的中心位置。分解尺度計算公式如下:
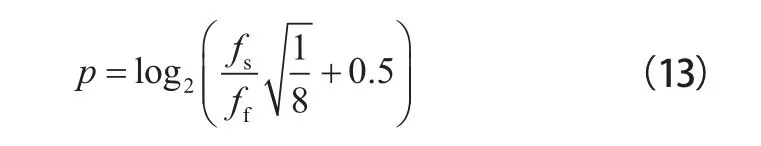
式中:為采樣頻率;為基頻。
本文中電力線通信信道噪聲的基頻分量為50 Hz,每個周期的采樣點數為500,信號的頻帶劃分為7,即對信號做6層分解。
3 算例分析
為驗證本章所提出的改進小波閾值去噪算法的有效性,實驗采用MATLAB軟件,在原信號中加入以電力線載波通信噪聲的數學模型生成的噪聲信號,采樣頻率為50 kHz,信號采樣長度為4 000個采樣點,16個周期(0.08 s)。
通常采用信噪比(Signal Noise Ratio, SNR)和均方根誤差(Root Mean Square Error, RMSE) 作為評價標準驗證去噪效果。其定義表達式如下所示:

SNR越高,RMSE越低,則證明該信號的去噪效果越好。選擇電力線載波通信信號作為原始數據,采用不同類型的小波基與軟、硬閾值函數相結合進行小波閾值去噪,具體去噪效果見表1所列。

表1 小波函數類型對去噪效果的影響
由表1可知,Db7小波基函數所對應的重構信號的信噪比和均方根誤差最優,故選擇Db7小波作為本次電力線載波通信信道去噪所使用的小波基函數。
電力線載波通信信號及小波閾值處理后的波形如圖3所示。
觀察圖3可知,信號中所含噪聲均得到極大抑制,3種閾值函數都有一定的去噪效果,新閾值函數的去噪效果要優于軟、硬閾值算法。從視覺效果看,信號恢復良好,SNR及RMSE也體現了本文算法的優越性。3種閾值函數的濾波效果見表2所列。

表2 3種小波閾值函數去噪效果對比

圖3 電力線載波信號去噪效果對比
4 結 語
本文提出了一種基于小波變換的改進閾值函數去噪算法,該算法改善了硬閾值與軟閾值函數的不足,通過對比不同小波函數并調節可變參數、,尋找適合電力線通信載波信號模型的更優參數。仿真結果表明,該改進閾值法與傳統閾值法相比,SNR最大,RMSE最小,重構信號更接近原始信號,證明了該方法的有效性。

