基于AFSA-BP神經網絡的光伏功率預測方法

陳文進，朱 峰，張童彥，張 俊，張鋒明，謝 棟，茹 偉，宋美雅，范 強

（1.國網浙江省電力有限公司，杭州 310007；2.國網浙江省電力有限公司紹興供電公司，浙江 紹興 312362；3.武漢大學 電氣與自動化學院，武漢 430072）

0 引言

氣候變化和能源安全是當前人類社會發展面臨的兩大嚴峻挑戰，在化石能源枯竭和環境變化的大背景下，世界各國都在努力探索轉變以往依賴化石能源的生產和消費模式［1-2］。隨著碳達峰、碳中和等能源戰略目標的提出，建設綠色電網、推動能源轉型，大力發展和使用清潔的可再生能源已勢在必行［3］。在眾多新能源行業發展過程中，光伏發電因其技術成熟、對環境零污染、應用范圍廣等特點，成為了能源轉型的關鍵［4］。隨著光伏裝機容量的不斷增加，對光伏輸出功率進行精確預測可以有效預防光伏接入后對電力系統的沖擊，為光伏的有效消納提供保障。

目前針對光伏功率預測的方法主要分為兩類［5］。一類是以氣象數據和實測功率數據為基礎，結合光伏場站的地理位置等參數建立預測模型與算法。文獻［6］提出對天氣類型進行多特征分析和提取，利用一階差分和因子分析法提取氣象數據的有效特征；文獻［7］運用互信息熵等相關性衡量指標，對影響光伏輸出功率的氣象因素進行定性和定量分析，挖掘氣象波動特性和功率數據的匹配關系；文獻［8］通過天氣分型，結合因果算法篩選不同天氣分型下的關鍵氣象因素，最后根據不同天氣類型劃分，進行分類預測。另一類是直接根據光伏出力的歷史數據進行預測，通過采用人工智能算法，結合歷史數據建立輸入變量和輸出變量之間的映射關系，預測未來的光伏功率輸出。這種方法對歷史數據的質量要求較高，大多具有較高的預測精度和泛化能力，主要包含BP（反向傳播）神經網絡法［9］、極限學習機［10-11］、支持向量機［12-13］等。其中BP 神經網絡具有非線性映射能力強、模型簡單等優點，在光伏功率預測方面得到了廣泛應用。文獻［14］提出一種將光伏發電樣本進行模糊聚類，再利用BP神經網絡進行分段預測的方法；文獻［15］通過相似變量選取相似日，利用動量法優化BP神經網絡進行預測；文獻［16］利用主成分分析法，建立基于特征提取的螢火蟲算法優化的BP神經網絡預測方法。以上方法均實現了較優的訓練效果及預測精度。

本文考慮引入AFSA（人工魚群算法），利用AFSA 優秀的內在并行計算能力和較快的尋優速度［17-18］，通過分析氣象數據與光伏功率數據的相關性，建立基于AFSA優化BP神經網絡的光伏功率預測模型。采用AFSA實現對BP神經網絡權值和閾值的優化，有效提高BP神經網絡的全局尋優能力，從而提高光伏輸出功率的預測精度。

1 數據清洗

光伏場站及氣象站測得的數據中，可能存在數據缺失、突變等問題，且氣象數據中包含大量、多維與光伏發電無關的氣象因素。使用低質量的數據進行模型訓練將對預測結果的準確度產生較大影響，因此需對數據進行清洗。

1.1 數據異常值剔除

在光伏輸出功率數據中，夜晚輻照度低，光伏輸出功率為零。大量零值數據將影響預測模型的性能與精度，需識別光伏輸出功率的零值數據并剔除。

光伏輸出功率與氣象數據都是通過數據采集設備采集得到的，獲得的原始數據中可能存在異常數據，需對其進行識別剔除。

本文采用3σ準則對數據進行清洗。由于光伏輸出功率與氣象數據大致服從于均值為μ、標準差為σ的正態分布，由正態分布的特性可知，數值A分布在(μ-3σ，μ+3σ)內的概率為：

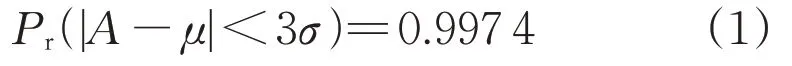
由于其概率極大，當數據值分布在(μ-3σ，μ+3σ)外時，可以將該數據視為異常值進行剔除。

1.2 氣象因素相關性分析

光伏場站測得的氣象數據包含氣溫、氣壓、相對濕度、輻照度等多種氣象因素，且多種氣象因素之間存在耦合關系，若考慮所有氣象因素進行光伏功率預測，將大大降低預測精度，因此需對氣象因素進行篩選，選取對光伏出力影響較大的氣象因素。

對氣象因素與光伏輸出功率進行相關性分析，采用Pearson 相關系數r表征不同氣象因素的相關性，計算公式為：

式中：a為數據樣本數；Pi、Qi為數據樣本；為樣本平均值。

計算得到的氣象因素與光伏輸出功率的Pear?son相關系數值如表1所示。

由表1 可知，在光伏場站測得的各氣象數據中，氣溫、總輻照度、法向直射輻照度、水平面散射輻照度與光伏輸出功率呈正相關關系，氣壓、相對濕度與光伏輸出功率呈負相關關系，且氣壓的相關程度最低。因此，在下文的仿真分析中，選取氣溫、總輻照度、法向直射輻照度、水平面散射輻照度這4個氣象因素作為預測模型的輸入變量，建立與光伏輸出功率相關的預測模型。

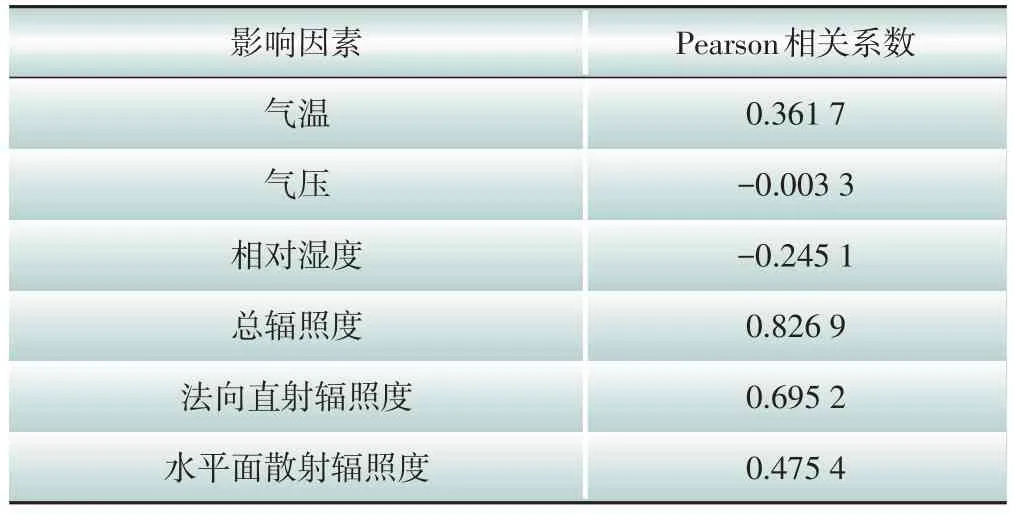
表1 氣象因素與光伏輸出功率的Pearson相關系數

1.3 數據歸一化處理

光伏輸出功率與氣象數據通常具有不同的數量級和單位，直接對其進行數據分析會影響預測模型的性能，需要對數據進行歸一化處理。此外，不同數量級的數據將會影響神經網絡的連接權值，導致神經元飽和，因此也需要對數據進行歸一化處理，計算公式如式（3）所示。當預測模型訓練和測試完成后，還需要對神經網絡的輸出值進行反歸一化處理，才能得到真實預測結果，式（4）為反歸一化的計算公式。

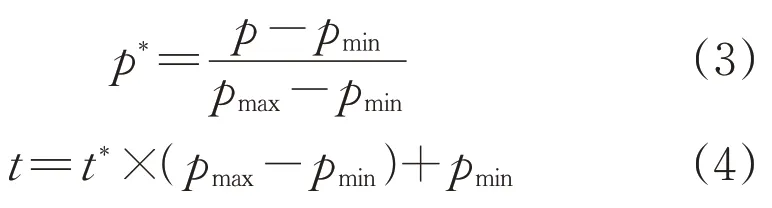
式中：pmax和pmin分別為原始序列的最大值和最小值；p為當前點的值；p*為歸一化后的數值；t*為神經網絡的輸出值；t為反歸一化后的數值。

2 基于AFSA-BP神經網絡的預測模型

2.1 AFSA

AFSA 由李曉磊在2001 年提出［19］，通過描述魚群的基本習性來模仿優化求解過程。假設人工魚的數量為Nf，第i條人工魚的狀態向量為Xi=(xi1，xi2，…，xik，…，xiN)，其中xik為待尋優的控制變量，N為待尋優變量的個數。第i條人工魚所在位置的食物濃度（目標函數）為Yi=f(Xi)。人工魚之間的距離為dij=‖Xi-Xj‖，其最大感知距離為dvisual，移動的最大步長為S，魚群擁擠度為δ。將預測模型的輸出值與實際數值的RMSE（均方根誤差）負值作為人工魚的目標函數Yi，評價每次迭代中人工魚位置的適應度值，即：

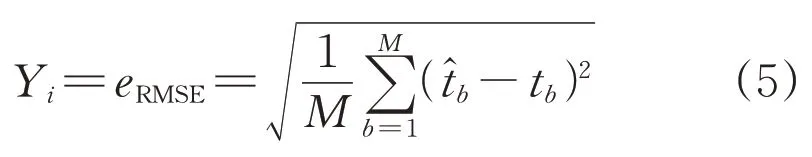
式中：eRMSE為RMSE 的值；M為預測模型輸出樣本數；和tb分別為預測模型輸出值和真實值。

AFSA 主要包括覓食行為、聚群行為和追尾行為。

1）覓食行為。人工魚在其感知范圍內（dij≤dvisual）隨機選擇另一個狀態Xj，如果得到的狀態目標函數Yj較優，則向新狀態移動一步。否則隨機移動一步。用數學表達式表示為：

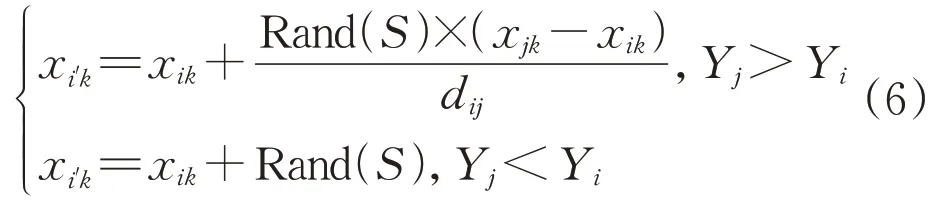
式中：k=1，2，…，N，xjk、xik、xi′k分別為狀態向量Xj、狀態向量Xi、下一步狀態向量Xi′的第k個元素。

2）聚群行為。人工魚通過探索感知范圍內（dij≤dvisual）同伴的中心點狀態Xc和中心點的目標函數Yc，計算公式為：

式中：nf為感知范圍內的同伴數量；xck和xjk分別為中心點的狀態向量Xc和第j個同伴狀態向量Xj的第k個元素。

否則人工魚執行覓食行為。

3）追尾行為。人工魚探索感知范圍內（dij≤dvisual）目標函數Y最優的同伴Xmax，若滿足Ymax>δYi，表明同伴Xmax處目標函數較優且不太擁擠，則向同伴位置Xmax移動一步，即：

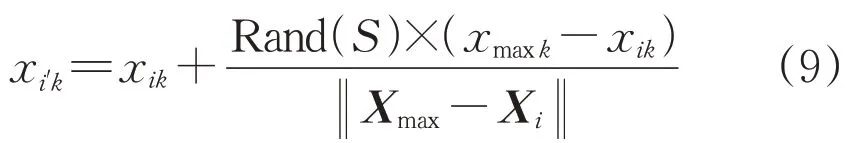
式中：xmaxk為狀態向量Xmax的第k個元素。否則人工魚執行覓食行為。

具體的參數設置如表2所示。

表2 AFSA參數設置

2.2 BP神經網絡

BP神經網絡于1986年由Rumelhart和McClel?land 首次提出，是一種利用梯度下降法按照誤差逆向傳播算法訓練的多層前饋神經網絡，是當前應用最為廣泛的神經網絡模型之一，其結構如圖1所示。

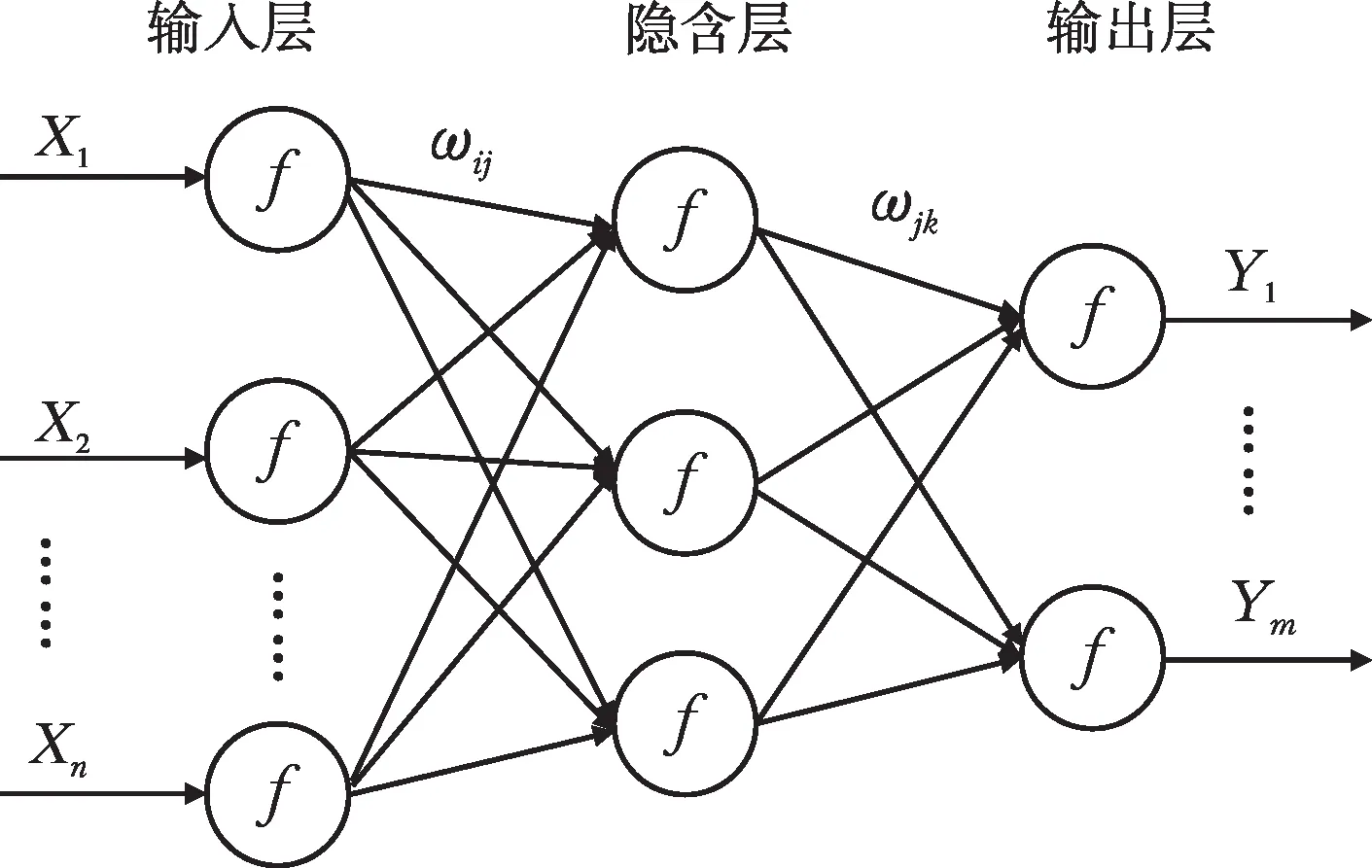
圖1 BP神經網絡結構

BP神經網絡具有非線性映射能力強、泛化能力強等優點，但同時存在學習速度慢、容易陷入局部最優等缺點，因此有待進一步研究。

本文采用的BP 神經網絡仿真參數設置如表3所示。

表3 BP神經網絡參數設置

2.3 AFSA-BP神經網絡預測模型

本文利用AFSA 算法對BP 神經網絡進行優化，以確定網絡的最優權值和閾值，提高光伏輸出功率的預測精度。AFSA-BP 預測模型的算法流程如圖2所示，其具體步驟如下：

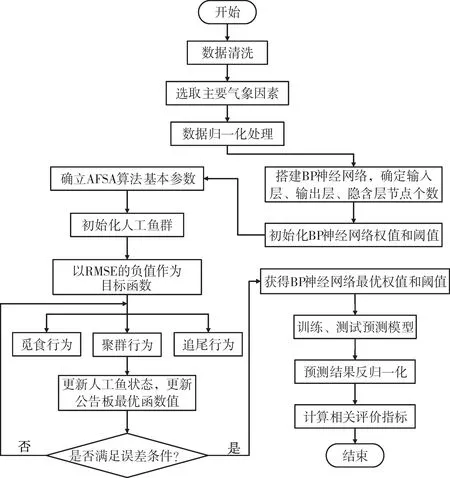
圖2 AFSA-BP預測模型算法流程

1）對搜集數據進行清洗。首先根據3σ準則對數據進行異常值的識別與剔除；其次計算各氣象因素與光伏輸出功率之間的Pearson相關系數，選取影響光伏出力的主要氣象因素；最后對數據進行歸一化處理。

2）初始化BP 神經網絡。構建BP 神經網絡，確定輸入層、輸出層和隱含層節點個數，其中隱含層節點數s由式（10）確定，初始化BP 神經網絡的權值和閾值。

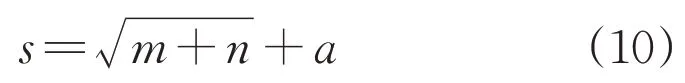
式中：n和m分別為神經網絡輸入層和輸出層的節點數；a為0～10的常數。

3）初始化人工魚群。確立人工魚群基本參數并初始化，將預測模型的輸出值與實際數值的RMSE負值作為人工魚的目標函數。

4）執行人工魚群優化算法。人工魚判斷當前狀態，執行覓食行為、聚群行為或追尾行為，從而更新BP神經網絡權值和閾值。計算當前人工魚目標函數值并與最優值進行對比，更新當前最優函數值。

5）判斷退出迭代條件。將當前最優值與誤差條件對比，若滿足誤差條件，則執行步驟6）；若不滿足誤差條件，則返回步驟4）。

6）訓練BP神經網絡預測模型。得到滿足誤差條件的最優權值和閾值，將其與訓練數據集代入神經網絡進行訓練，得到預測模型。

7）預測結果輸出。將測試集代入訓練好的預測模型，對得到的預測結果進行反歸一化處理，得到與原始數據量綱單位一致的數據，輸出結果并計算相關評價指標。

3 仿真分析

為驗證所提方法的優越性，本文采用2018 年某光伏電站10—12 月數據進行仿真分析，經清洗后的數據集包括每15 min采樣的氣溫、總輻照度、法向直射輻照度、水平面散射輻照度數據以及對應的光伏場站輸出功率數據。

圖3為各氣象數據與對應的光伏輸出功率數據散點圖。由圖3可見，總輻照度與光伏輸出功率相關性最大，法向直射輻照度次之，氣溫相關性最小，符合表1計算結果。

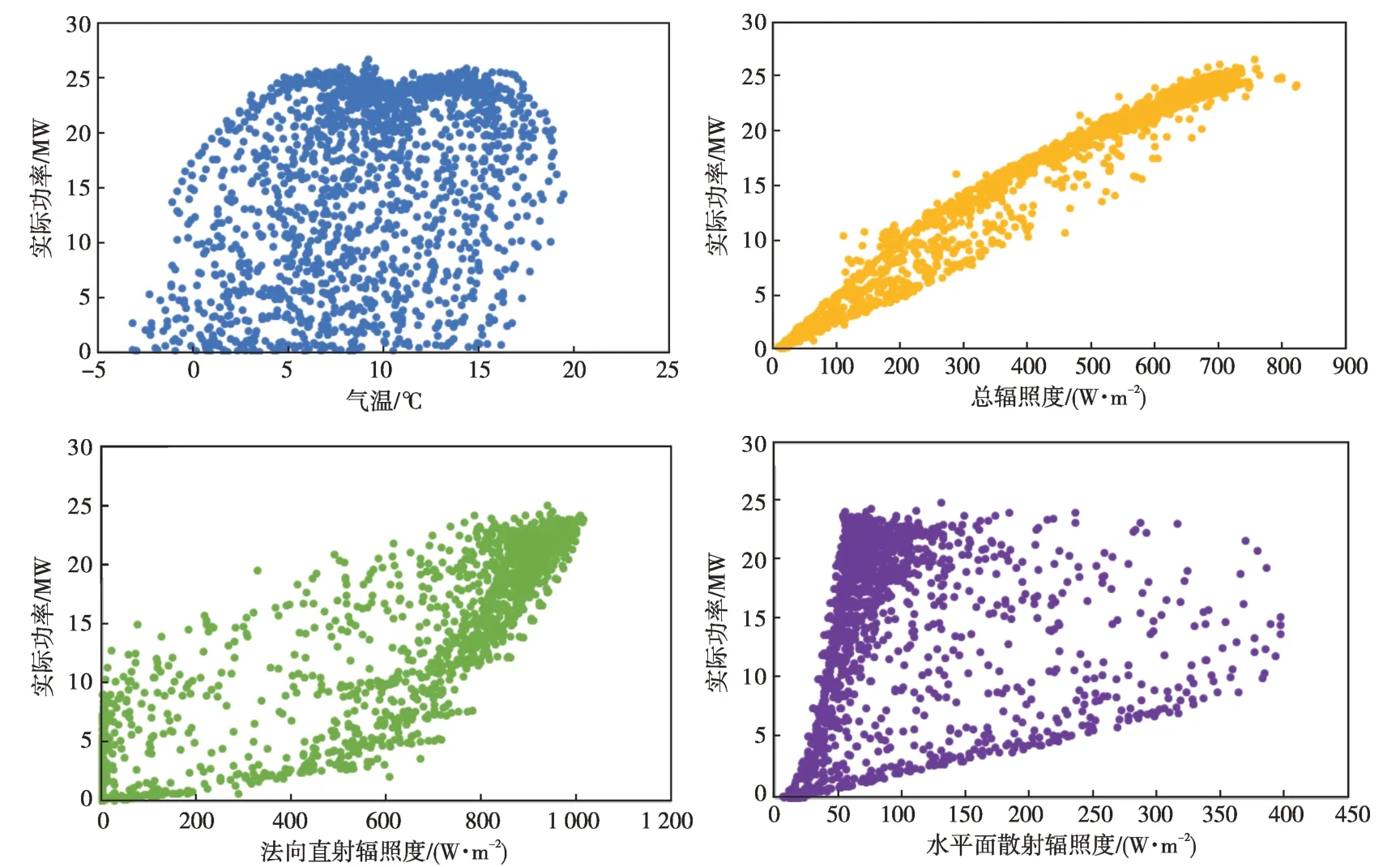
圖3 氣象與功率數據散點圖

3.1 評價指標

在衡量預測模型的預測精度時，常用的評價指標包括RMSE、MAE（平均絕對誤差）、MSE（均方誤差）和MAPE（平均絕對百分比誤差）。RMSE計算公式見式（5），其余指標計算公式如下：

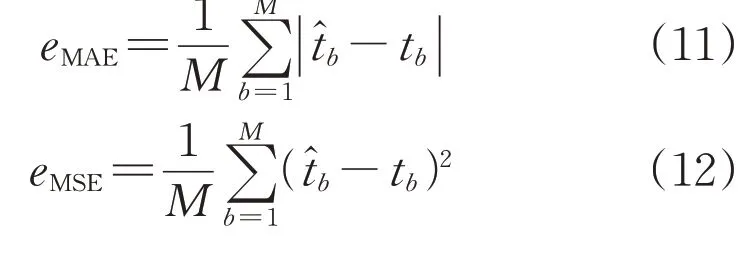
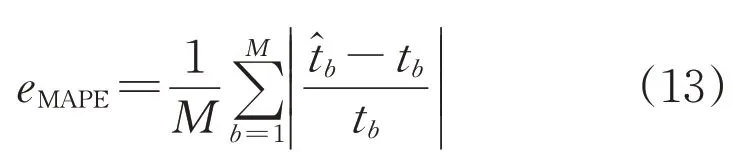
式中：eMAE、eMSE、eMAPE分別為MAE、MSE、MAPE的值。

3.2 仿真結果

文獻［20-22］中指出，運用GA（遺傳算法）優化神經網絡和PSO（粒子群優化）算法優化神經網絡，相較于直接運用BP神經網絡進行預測的結果更優，因此本文引入GA-BP 和PSO-BP 方法作為對照。將清洗后的數據集劃分為訓練集和測試集，其中前90%的數據作為訓練集，剩下10%的數據作為測試集，分別利用僅BP神經網絡、GABP、PSO-BP、AFSA-BP這4種方法進行建模預測，仿真軟件為MATLAB R2020b。相關參數設置見表4和表5。圖4為4種方法的預測結果。

表4 GA-BP參數設置

表5 PSO-BP參數設置

對4 種方法的預測結果分別計算RMSE、MAE、MSE、MAPE，見表6。

由圖4、表6可知，GA-BP、PSO-BP 和AFSA-BP 方法在預測精度上相較于僅BP 神經網絡均有提升，其中AFSA-BP 預測精度最高，與原始數據曲線擬合程度最優，相關誤差評價指標最低。特別是在預測結果中段，可能由于云層遮擋、陣雨等天氣原因，導致輸出功率出現了大幅波動，AFSA-BP 方法仍有較優的預測效果。此外，PSO-BP比GA-BP具有更高的預測精度，與文獻［21-22］中相關結論相符。

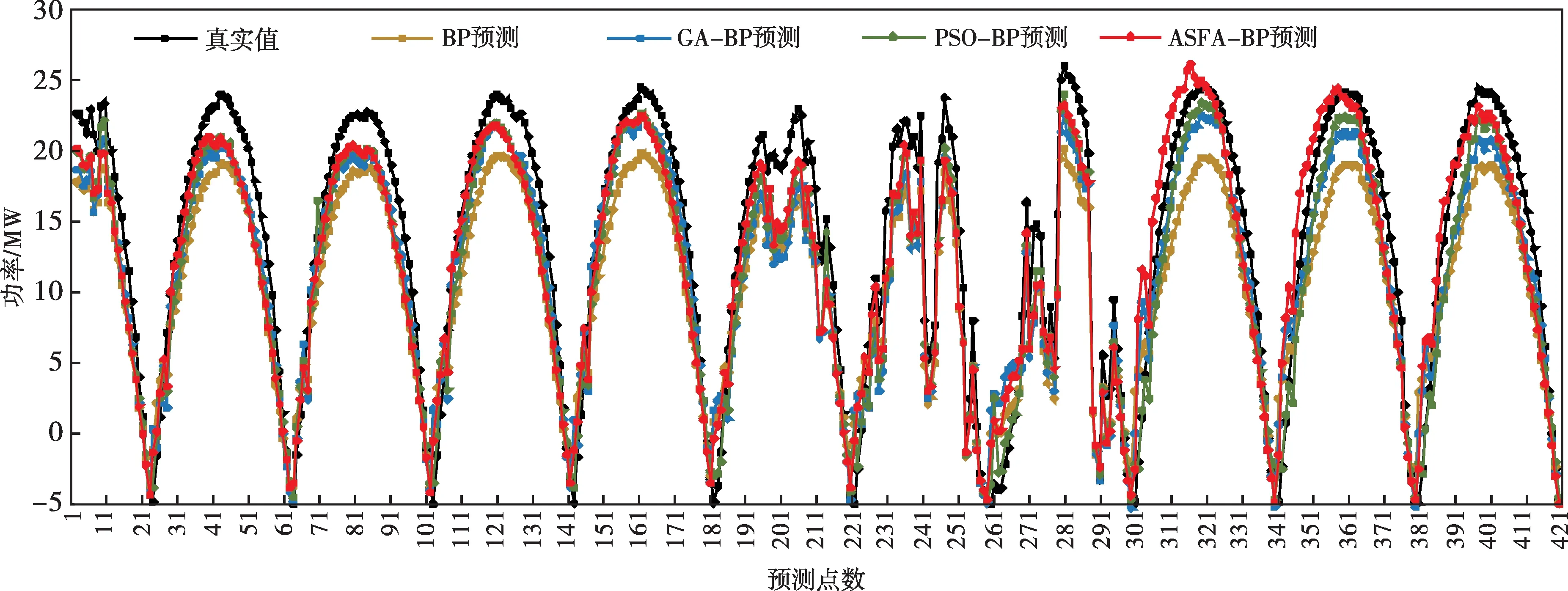
圖4 4種方法預測結果

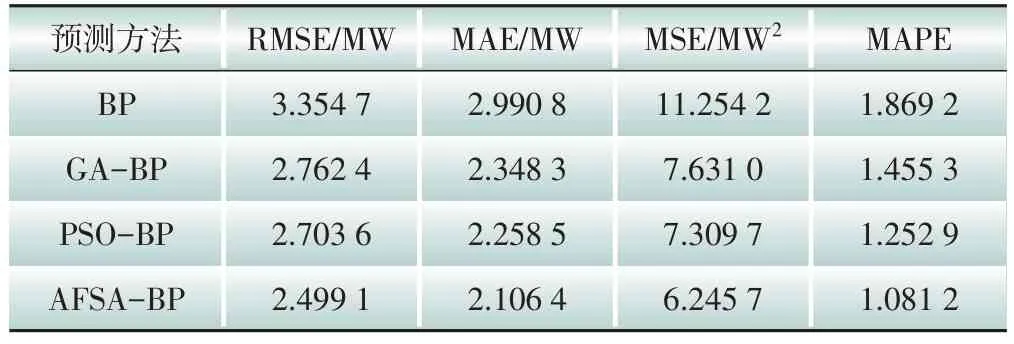
表6 4種方法誤差對比

對4 種預測方法的訓練耗時進行比較，結果見表7。可以看出，對BP 神經網絡的權值和閾值進行優化明顯增加了訓練耗時。相較于GA 與PSO算法，利用AFSA對BP神經網絡的權值和閾值進行優化，訓練耗時較短。由此可見，使用AFSA優化BP神經網絡的權值和閾值能有效提高光伏輸出功率的預測精度，同時訓練耗時較短，在光伏功率預測方面具有較高的優越性。

表7 4種方法訓練耗時對比

4 結語

為提高光伏輸出功率的預測精度，本文提出了一種基于AFSA-BP神經網絡的功率預測方法，結果表明：

1）通過對所測數據的清洗及篩選，能有效降低氣象數據的維度，提高數據質量，從而提高了計算速度，為后文模型的精度提升奠定基礎。

2）與僅使用BP 神經網絡、GA-BP、PSOBP 等方法相比，AFSA-BP 方法具有更高的預測精度，與原始數據曲線擬合程度更優，誤差評價指標更低。

3）利用AFSA-BP 方法的模型訓練耗時相對較短。

本文提出的優化模型在光伏輸出功率預測方面具有一定的應用推廣價值，有助于促進光伏的有效消納，助力“雙碳”目標的實現；同時，可在電力系統調度、儲能等相關方面發揮作用，提高電力系統的穩定性。