基于MSSST和強化輕量級卷積神經網絡的有載分接開關運行工況識別

魏 敏，王劉旺

（1.國網浙江省電力有限公司嘉興供電公司，浙江 嘉興 314033；2.國網浙江省電力有限公司電力科學研究院，杭州 310014）

0 引言

作為大型變壓器中的關鍵部件組成，有載分接開關承擔著無功調節和穩定功率的重要功能，由于實際工程現場分接開關切換十分頻繁，其故障發生率一直居高不下。異常工況下的分接開關對于變壓器穩定運行形成了巨大的安全隱患，若不及時甄別處理，很容易引發電網連鎖事故，因此有載分接開關工況識別對于保障整個電力系統安全可靠運行具有重要意義［1-2］。

近些年，相關領域學者圍繞著有載分接開關工況甄別開展了大量研究工作，相繼提出了油液溶解氣體分析［3］、電弧監測［4］、聲學分析［5］、溫度分析［6］等一系列工況識別策略。有載分接開關切換過程屬于瞬態觸發動作，機構各部件間的摩擦碰撞將導致非平穩非線性振動，所拾取的振動信號中包含豐富的狀態信息，因此振動分析已成為分接開關狀態監測的重要技術手段［7-8］。

不同運行工況下，分接開關切換過程產生的時域振動信號差異性較小、可區分性較差，相比于單一時域特征，通過合理的時頻分析手段將原始時域特征轉化為物理意義更為明確的二維時頻特征，可放大信號特征間的差異，便于后續狀態分類辨識。現有文獻報道中，STFT（短時傅里葉變換）、CWT（連續小波變換）、WVD（魏格納威爾分布）是常用的變換域特征處理手段，但存在時頻聚焦性不足、分析靈活性欠佳的弊端。最近，相關學者提出一種MSSST（多重同步壓縮S變換）理論［9］，其本質是在ST（S 變換）基礎上進行多重同步壓縮處理，從而獲取能量更為集中、表達更為清晰的二維時頻特征。本文從描述振動信號時頻特征角度出發，將MSSST理論引入電氣設備狀態監測診斷領域，用于提升信號特征表達維度，充分挖掘分接開關振動信號中蘊含的特征信息。

近些年，深度學習理論在生物特征識別、大數據信息挖掘等領域迅速普及，作為深度學習理論中最具代表性的網絡結構框架，CNN（卷積神經網絡）在電力設備狀態監測診斷領域也得以成功應用［10］。經典的CNN 運算量及模型參數數量較大，對計算機硬件水平及存儲空間要求較高，而實際工程現場設備的計算能力及存儲空間有限，因此CNN 的固有缺陷限制了其在工程現場的普及應用［11］。為了彌補這一缺陷，Howard［12］通過一種新穎的分離卷積操作替換標準的卷積運算，在傳統CNN 模型基礎上開發出MobileNetv1 輕量級CNN模型，可有效縮減模型參數數量及訓練時間，但是存在輸入層內核數量固定的瓶頸。最近，Sandler 等人［13］提出一種MobileNetv2 輕量級CNN模型，其最大亮點是能夠在保證計算精度前提下大幅提升訓練效率，因此本文嘗試將其引入電氣設備狀態監測診斷領域，并在該模型基礎上融合Adaboost 自適應提升機制，提出一種分類能力更為優良的RLCNN（強化輕量級卷積神經網絡）模型。

基于以上闡述，本文利用MSSST將一維時域振動波形轉換為二維時頻域圖像，擴充特征表達維度后，通過RLCNN 模型對圖像進行層次化的解析及分類，提出一種新穎的變壓器有載分接開關多工況識別方法。該方法充分發揮了MSSST算法在信號時頻特征刻畫上的優勢以及RLCNN 模型在多狀態分類方面的強大性能，有望實現變壓器有載分接開關運行工況的準確判定。

1 MSSST

1.1 MSSST基本原理

對于一個給定信號x(τ)，其ST表達式為［9］：

由式（1）可知，ST 的窗函數比較靈活，其寬度可根據分析頻率ω的變化而變化，在低頻區域窗寬較大而在高頻區域窗寬較窄，但ST的時頻聚焦性仍不夠理想，存在一定提升空間。為此，相關學者借鑒多重同步壓縮變換的思想，在ST基礎上進行多重同步壓縮處理，提出了MSSST 算法，具體表達式為：

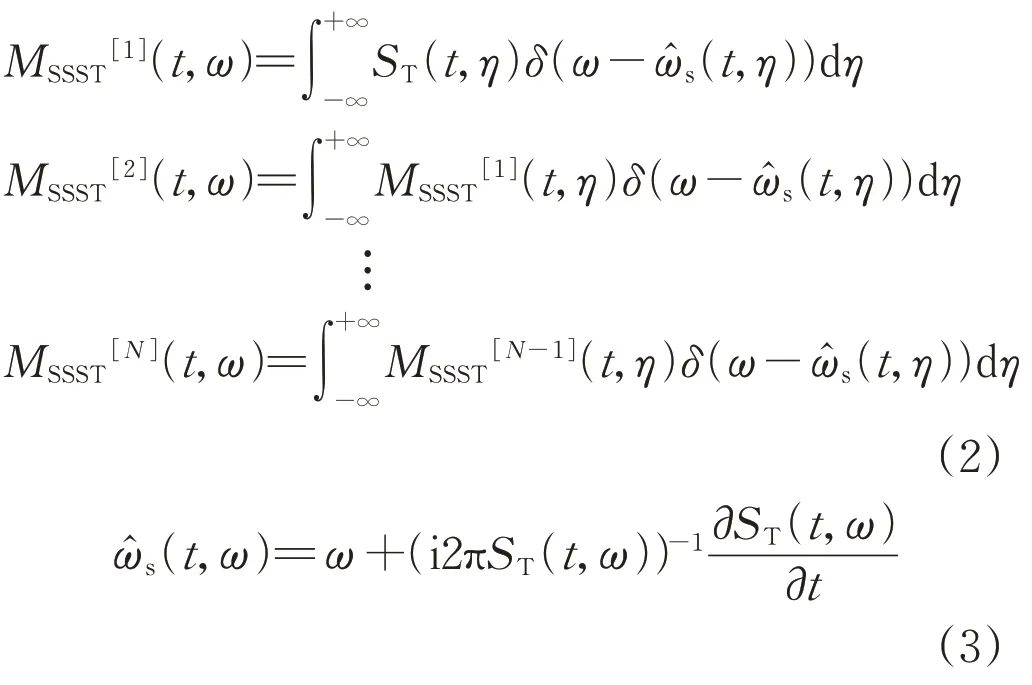
式中：δ(·)為狄拉克函數；η為表達式變換中間變量；MSSST[N](t，ω)為通過同步壓縮算子迭代N次所得結果；(t，η)為瞬時頻率估計值。將MSSST[1](t，η)代入MSSST[2](t，η)可得：

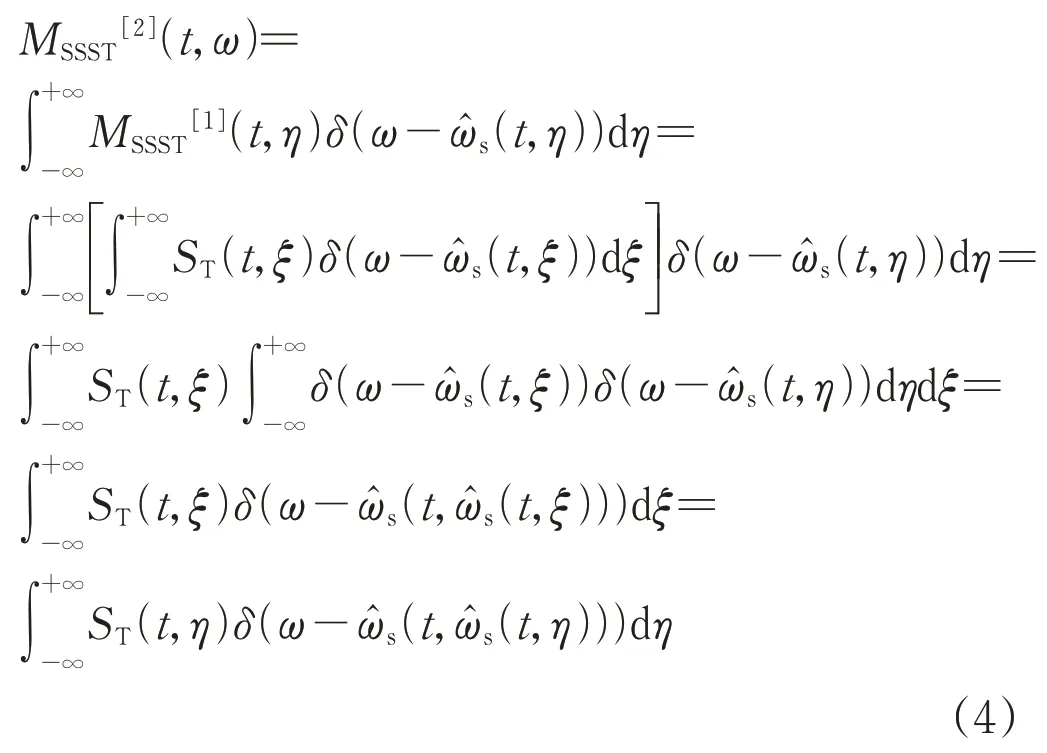
式中：ξ為表達式變換中間變量。

與上述過程相似，利用同步壓縮算子迭代N次后，時頻能量重分配結果可表示為：

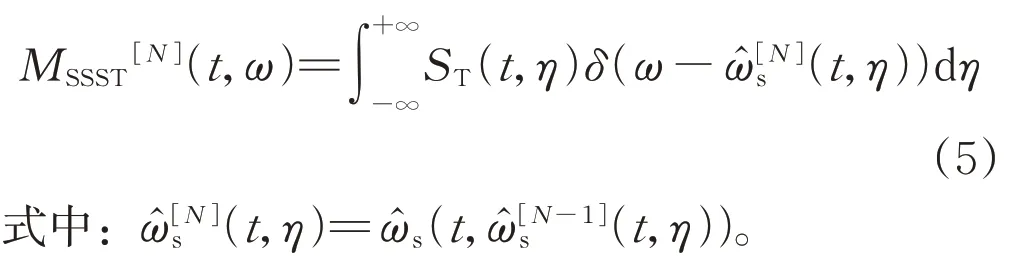
每一次迭代運算，MSSST通過構造一個新的瞬時頻率估計值來實現模糊ST 能量的重排分布，經過多次迭代運算，所得瞬時頻率估計值逐漸接近原始信號的真實頻率，從而有效提高二維圖像的時頻聚焦性。與STFT、CWT、WVD 等時頻分析方法類似，利用MSSST算法對一個給定信號進行分析處理，所得二維圖像MSSST[N](t，ω)反映了在任意時間點t及頻率點ω處信號的能量強度。

1.2 MSSST時頻分析能力驗證

為驗證MSSST算法的時頻分析能力，模擬生成一個多分量瞬態沖擊響應信號m（t）：

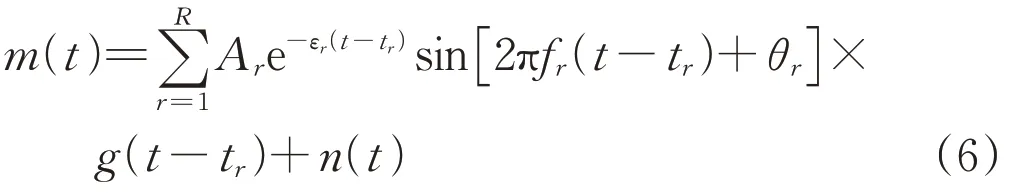
式中：R為瞬態沖擊響應分量個數；g（t）為階躍響應函數；Ar、εr、fr、tr、θr分別為第r個響應分量的振動幅值、阻尼系數、振動頻率、發生時刻、初始相位；n（t）為添加的高斯白噪聲。

設置m（t）的數據點數Ns=1 800，采樣頻率fs=6 000 Hz，信號時長為0.3 s，所添加高斯白噪聲n（t）均值為0、標準差為0.05。本文利用3 個瞬態沖擊響應分量來構造模擬信號m（t），即R=3，這3個分量的相關參數設置如表1所示。為了增大信號時頻特征分辨刻畫的難度，設置這3個瞬態沖擊響應分量在時域上相互交疊，均產生于0.1 s時刻。

表1 模擬信號參數設置

模擬信號波形及頻譜如圖1所示：時域波形呈現為能量逐漸衰減狀態，較為簡單；頻域分析中出現了3個明顯的譜峰，分別對應模擬信號中包含的300 Hz、1 100 Hz、1 600 Hz頻率成分。

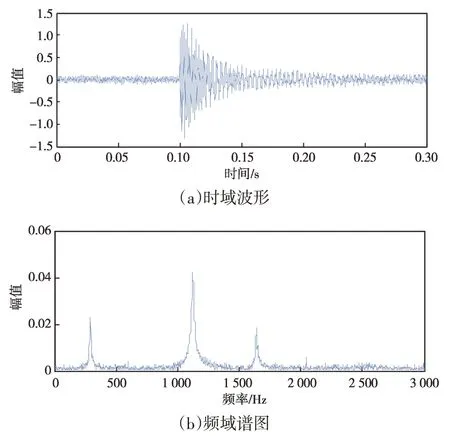
圖1 模擬信號波形及頻譜

分別利用MSSST、ST、MSST（多重同步壓縮變換）、STFT、CWT、WVD 等時頻分析方法對該模擬信號進行分析處理，用于對比驗證MSSST算法在時頻特征刻畫方面的優勢，結果如圖2所示，為了更為清晰地對比分析，僅展示了時間軸0.08～0.18 s、頻率軸0～2 000 Hz范圍內的時頻特征。通過觀察可以發現：MSSST算法所得分析結果時頻聚焦性最佳、分辨率最高，模擬信號中包含的3個頻率成分均被清晰準確表達，并且沒有多余背景干擾成分；MSST和CWT算法雖然也能夠分辨出模擬信號中時域相互交疊的3個頻率成分，但是分析效果與MSSST 相比存在一定差距；ST、STFT、WVD 算法所得分析結果則不夠理想，聚焦性差、頻率成分交叉等因素導致未能準確表達原始信號的時頻特征。

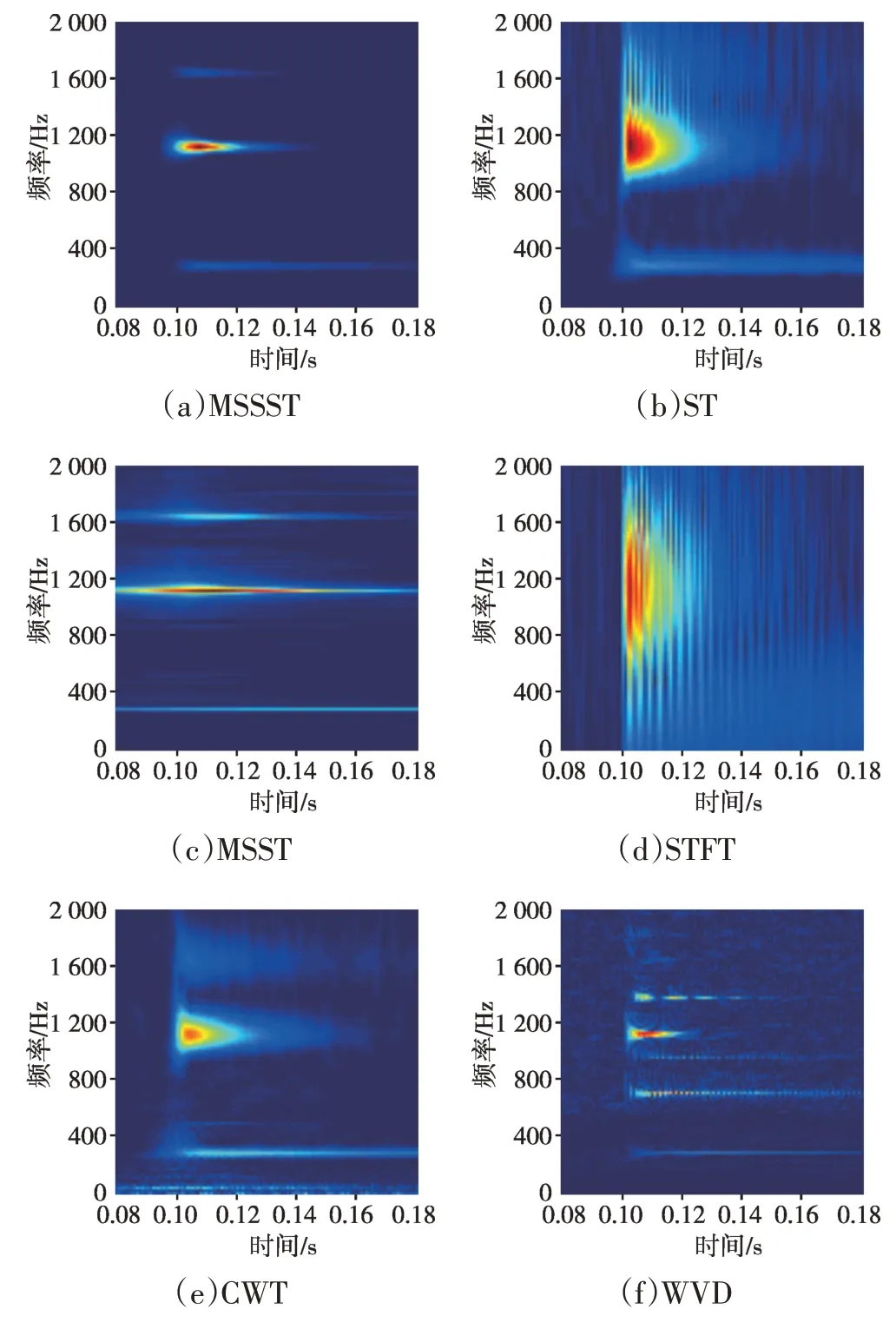
圖2 模擬信號不同時頻分析方法處理結果

為進一步定量評價MSSST算法的性能，本文利用Rényi熵指標對不同時頻分析方法所得結果進行量化計算對比。Rényi熵指標是信息評價標準中衡量二維圖像復雜度的最佳通用指標，對于任意一個二維圖像，如果所得熵值越小，表明圖像混亂程度越低，能量聚焦性越好；反之熵值越大，表明圖像混亂程度較高，能量聚焦性較差。Rényi熵Ra的計算表達式為［14］：

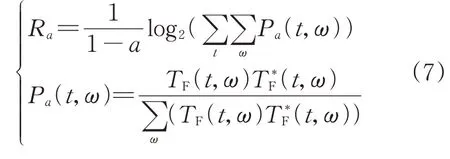
式中：a為Rényi 熵的階次；Pa(t，ω)為單位能量信號的概率分布函數；TF(t，ω)為時頻分布系數，(t，ω)為TF(t，ω)的共軛。

借助式（7）分別計算圖2 中各個二維時頻圖像對應的Rényi 熵值，本文取Rényi 熵階次a=3，所得結果如圖3 所示。圖3 中，MSSST 算法所得時頻分析結果對應的熵值明顯小于其他對比方法，表明通過MSSST所得時頻分析結果能量聚焦特性最佳，能夠更清晰、準確地表達信號時頻特征。

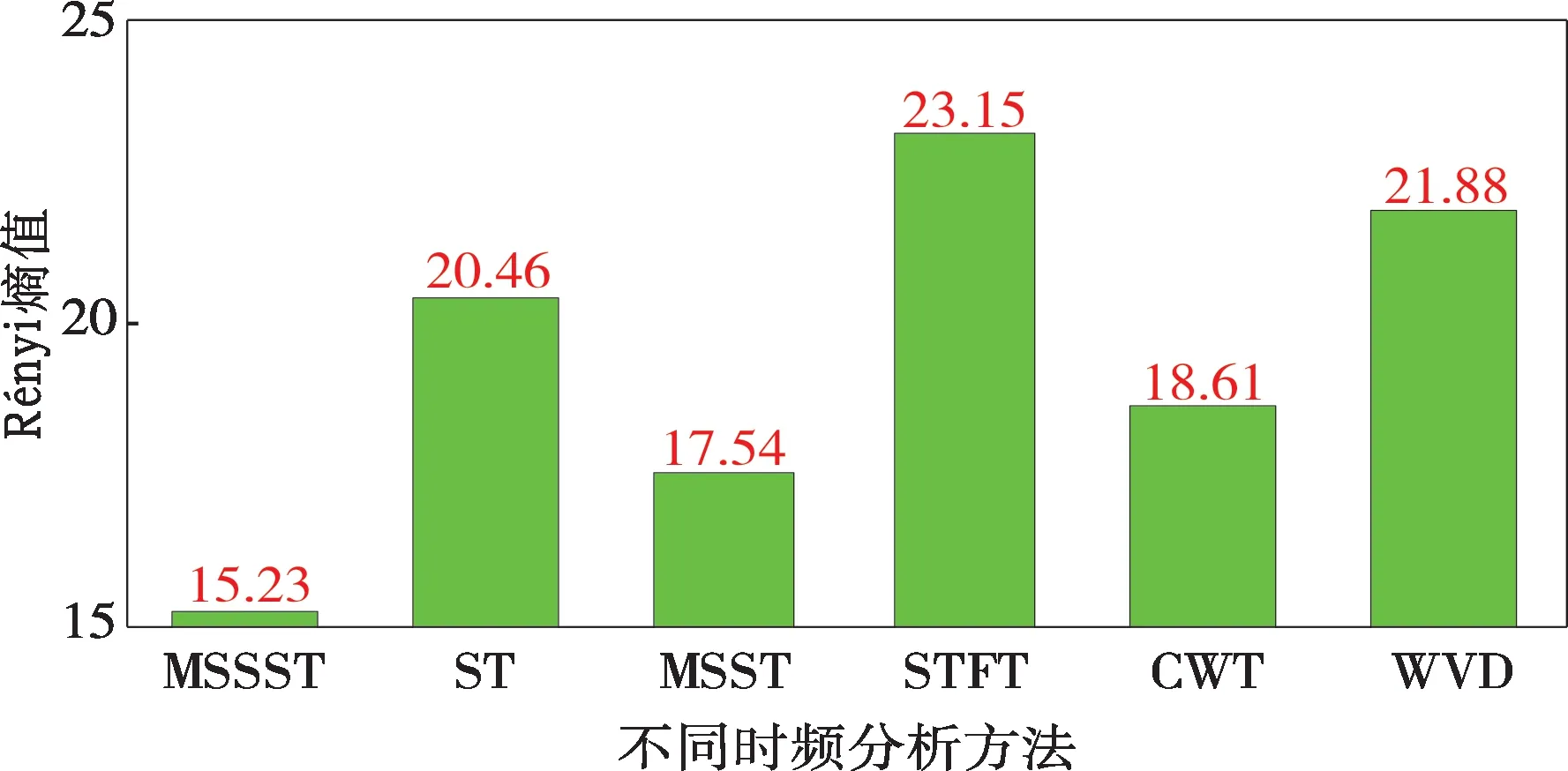
圖3 不同時頻分析方法Rényi熵值

2 RLCNN

2.1 MobileNetv2輕量級CNN

作為一種代表性深度學習框架，CNN 模型通過構造多個卷積核并結合稀疏連接、權重共享、時空域降采樣，對輸入樣本進行逐層卷積運算及池化處理，從而實現樣本隱含拓撲結構特征的逐級提取。CNN 模型主要由圖4 所示輸入層、卷積層、池化層、扁平層和全連接層構成。卷積層由多個卷積核組成，每個卷積核中元素分別對應一個權重值和一個偏差量，對輸入樣本進行卷積運算能夠快速挖掘其隱含特征；經由卷積層所挖掘的樣本特征被輸送到池化層實現參量縮減，處理方式包括最大池化、平均池化等；池化層處理后的數據被進一步輸送到扁平層，實現多維至一維向量的轉換；最后，通過全連接層獲取最終所需結果［15］。

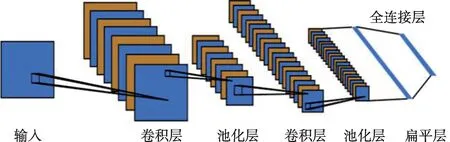
圖4 CNN模型

傳統CNN模型參數數量及運算量龐大，所需存儲空間較大，對硬件配置要求較高，不利于工程現場普及應用。而MobileNetv2 輕量級CNN 模型在卷積運算時采用一種具有線性瓶頸單元的逆向殘差結構（如圖5所示），相較于分離卷積操作運算量更小、準確率更高，該模型能夠在計算速度和識別準確率之間尋求最佳平衡，有利于其在工程現場計算平臺中推廣應用。

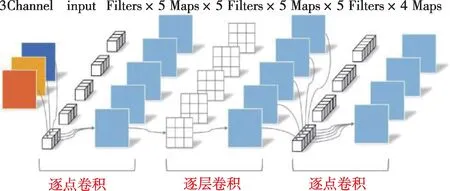
圖5 MobileNetv2模型卷積運算

2.2 Adaboost自適應提升機制

Adaboost 自適應提升機制的核心思想是在訓練樣本集中生成一系列權重系數，在此基礎上對訓練樣本集進行調整以生成多種假設條件，通過增大前一個網絡模型錯分樣本的權重來提高下一個網絡模型的識別準確率，因此該機制能夠充分利用有限訓練樣本集獲得更好的識別效果［16］。Adaboost 在迭代運算過程中，利用多分類指數損失函數的階段性加法建模，并依據訓練樣本集加權誤差最小化原則不斷更新權重系數。隨著迭代過程不斷推進，正確識別的樣本集權重逐漸減小，而被誤識別的樣本集則被賦予更大權重。其實現步驟概述如下：

步驟1，假設訓練集樣本類別k=1，2，…，K，樣本數為V，初始化訓練集權重ωi=1/v（v=1，2，…，V）。

步驟2，設置最大迭代次數為M，執行m=1～M的迭代運算過程。

1）利用權重為ωi的訓練集訓練網絡模型Tm(·)。

2）計算識別誤差err，m：

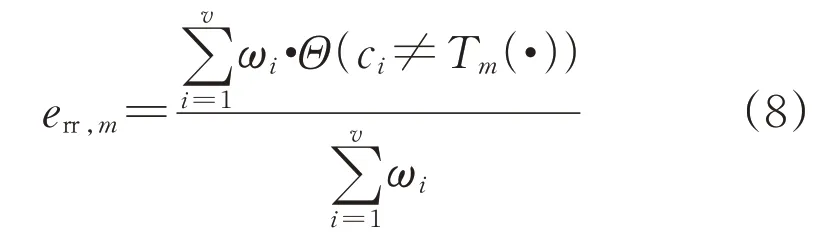
式中：ci為實際類別標簽；i代表標簽序號；v代表樣本序號；Θ(·)為指示函數，括號中內容為真時取值為1，反之指示函數取值為0。

3）根據所得識別誤差重新計算權重系數：

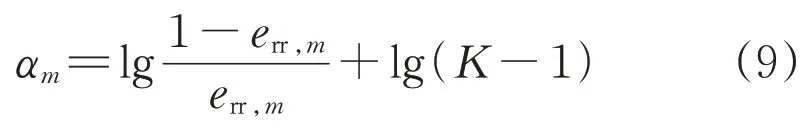
式中：αm為權重系數。

4）更新權重：

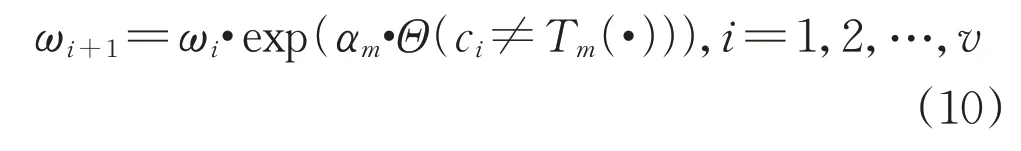
5）對權重進行歸一化處理。

步驟3，獲得最終識別結果C：

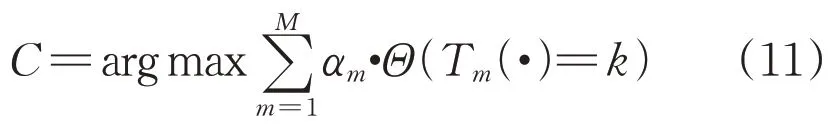
2.3 基于MobileNetv2-Adaboost 的RLCNN模型

實際工程中，神經網絡模型的訓練效果通常受數據集樣本大小、維度及總量的影響，為了在有限訓練樣本集條件下獲得最佳識別效果，提高變壓器有載分接開關不同運行工況的辨識準確率，本文結合Adaboost 自適應提升機制在集成學習方面的能力，以及MobileNetv2 輕量級CNN 在圖像識別領域的優勢，提出一種基于MobileNetv2-Adaboost 的RLCNN 模型，該模型通過Adaboost自適應提升機制對多個MobileNetv2網絡進行強化學習訓練，并將所有網絡輸出結果按不同權重進行組合，從而獲得更高的識別準確率，RLCNN實現流程如圖6所示。

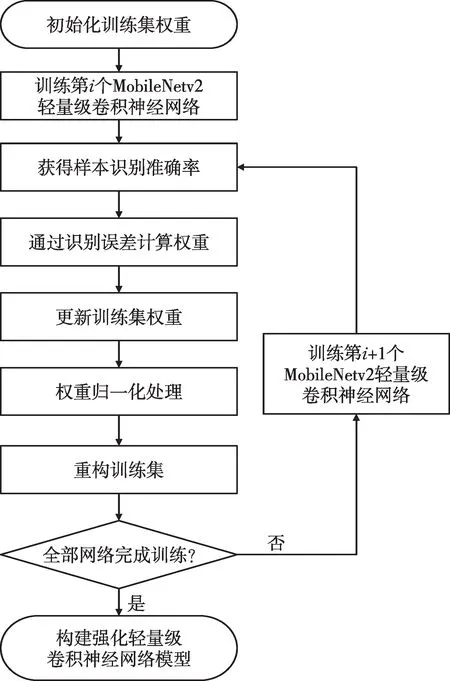
圖6 RLCNN模型實現流程

3 實驗驗證

3.1 數據采集

為了驗證本文所提識別方法的有效性，在CM型110 kV 有載分接開關工況模擬實驗臺上開展實驗研究。實驗臺結構如圖7（a）所示，主要包含油箱、齒輪盒、電動機構、絕緣筒、分接選擇器、切換開關。分別設置分接開關正常運行、主彈簧松動、主觸頭磨損和傳動機構卡澀4種類型的運行工況。振動傳感器采用東華1A110E型壓電式加速度傳感器，該傳感器具有分辨率高、抗干擾能力強的優點。采用粘合安裝方式將壓電加速度傳感器布置在分接開關頂端及側壁位置，如圖7（b）所示，用于采集開關切換動作產生的振動信號，設置采樣頻率為20 kHz，利用NI9234 采集卡實現模/數轉換后輸入到計算機中進行數據存儲及后續分析處理。實驗過程中，將分接開關置于充滿油液的油箱中，模擬分接開關在變壓器油箱中的運行環境，使振動信號更接近實際工程環境。

圖7 有載分接開關實驗臺

整個實驗過程中，通過加速度傳感器分別采集分接開關正常工況及3種故障工況產生的振動信號，每種工況取500組樣本信號，每組樣本信號包含10 000個數據點，整個數據集共包含2 000組樣本。從中隨機抽取80%樣本作為訓練集用于訓練RLCNN 模型參數，剩余20%樣本作為測試集用于評估本文所提方法的識別能力，因此構造的訓練集樣本為1 600 組，測試集樣本為400 組。圖8為分接開關不同工況下測取的樣本信號時域波形及頻域譜圖，其中g為重力加速度。通過對比可以發現，分接開關傳動機構卡澀樣本波形與其他運行工況下的波形存在一定差異，而正常工況與主彈簧松動、主觸頭磨損工況下切換動作所產生的樣本信號波形及譜圖的差異不明顯。尤其是正常工況和主觸頭磨損工況相比，二者的樣本信號波形及譜圖極為相似，究其原因主要由于觸頭磨損對于分接開關整體動態特性所造成的影響不明顯。總體來看，僅憑借時域波形及頻域譜圖觀察難以進行特征捕捉，無法快速有效地區分出有載分接開關的不同運行工況。

3.2 分接開關工況辨識

下面利用本文提出的方法對變壓器有載分接開關運行工況進行自動辨識。首先，利用MSSST時頻分析算法對樣本信號進行處理，將一維時域波形轉換為二維時頻圖像，實現特征增維，便于后續RLCNN模型的訓練及測試。以圖8中分接開關不同工況樣本信號為例，經MSSST處理后所得結果如圖9所示，為了表達更為清晰，僅展示時間軸0.05～0.3 s、頻率軸0～8 000 Hz 范圍內的時頻特征。對比后可發現：有載分接開關正常工況下切換動作所產生的振動信號能量主要分布在0～2 000 Hz及4 000～6 000 Hz范圍內；主彈簧松動狀態下機構剛度有所下降，振動信號能量分布稍有偏移，主要分布在0～2 000 Hz 及4 500～7 000 Hz 范圍內；分接開關主觸頭磨損狀態對于機構整體動態特性影響較小，其時頻分析結果與正常工況下所得結果十分相似；傳動機構卡澀狀態下，分接開關完成整個切換動作所需時間有所延遲，能量分布主要集中在3 500～6 500 Hz 范圍內，不同工況樣本所呈現的二維時頻圖差異性更大，可區分性有所提升。

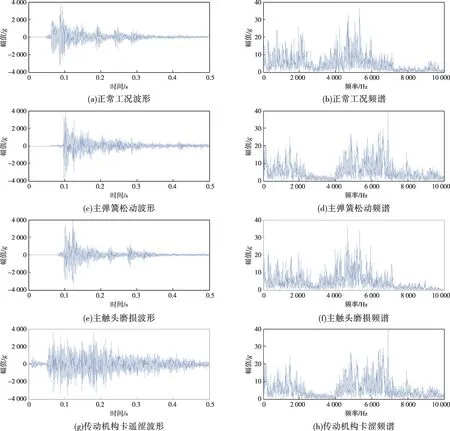
圖8 不同工況樣本波形及頻譜

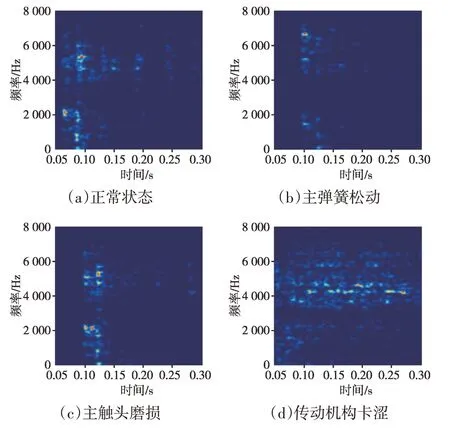
圖9 不同工況樣本MSSST處理結果

利用Python 編程語言在Windows 平臺上搭建RLCNN 模型，相應的計算機硬件水平為Intel Core i7-8700k 處理器、32 GB 內存環境、Nvidia GTX 1080Ti GPU。參考文獻［11］對單一Mobile?Netv2網絡結構參數進行設置，具體參數設置情況如表2 所示。其中擴展因子可調整輸入圖像尺寸，除第一層外其他層步長均設置為1，空間卷積運算均使用3×3卷積核。

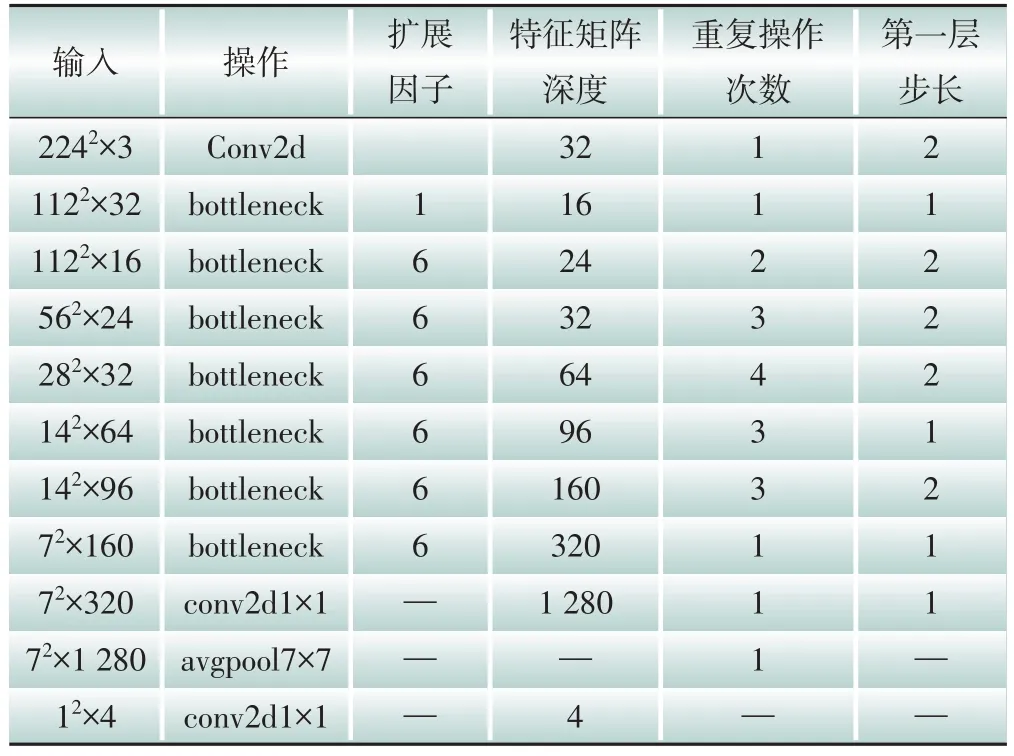
表2 MobileNetv2網絡結構參數

全面考慮訓練集樣本數量、類別及長度、網絡結構復雜度、計算機內存大小、處理器性能等諸多影響因素，本文對網絡模型超參數設置情況如下：在不爆顯存條件下，應該盡可能地選用較大的批數據尺寸，在此設置單一MobileNetv2網絡批數據大小為32；學習率的選取則參考文獻［13］，直接設置為0.000 1；在訓練過程中利用Model?Checkpoint函數在每個迭代周期后檢查模型識別準確率是否提升來保存最佳模型，最終設置迭代輪次為40，可防止因迭代次數過多而造成的過擬合現象；由于樣本集包含了分接開關4種不同狀態樣本，因此樣本類別數為4；損失函數選取為交叉熵。

構建RLCNN 模型時，需要通過Adaboost 自適應提升機制集成多個MobileNetv2網絡，由于目前缺少理論借鑒及相關文獻報道參考，本文通過多次實驗來確定網絡數量。對比發現，當MobileNetv2網絡數量為5時，所構建RLCNN模型的識別準確率達到穩定狀態，之后隨著網絡數量增大，準確率不再出現明顯提升。因此，綜合考慮模型的可靠性及運算負擔，本文利用5 個單一MobileNetv2網絡進行集成來構建RLCNN 模型。在Adaboost迭代運算過程中，通過訓練樣本集加權誤差最小化原則來不斷更新各個單一MobileNetv2網絡的權重系數，訓練結束后各個網絡可自動獲得其最佳權重配比，從而使得所構建的RLCNN 模型具有良好的整體識別性能。

利用MSSST算法處理所得樣本信號獲取二維時頻圖像后，將其輸入到RLCNN 模型中進行訓練及測試。為了保障識別結果的可靠性，在網絡參數相同條件下識別30 次，并計算識別結果的平均值，最終測試集樣本的平均識別準確率高達99.32%。為驗證基于Adaboost自適應提升機制的RLCNN 模型的優勢，繪制出單一MobileNetv2 網絡在訓練集和測試集上的識別準確率及損失值，如圖10和圖11所示。從圖中可以看到，隨著輪次的增加，訓練集和測試集樣本的識別準確率均逐漸增大，到第25輪時識別準確率接近95%后不再提升，而訓練集和測試集樣本的損失值也在第25輪時處于收斂狀態，下降至0.1后不再變化。就呈現結果來看，單一MobileNetv2網絡的識別效果仍存在一定提升空間，而通過Adaboost 自適應提升機制將多個輕量級CNN 進行融合，所構建的RLCNN模型則優勢更加明顯。

圖10 單一MobileNetv2網絡訓練及測試準確率

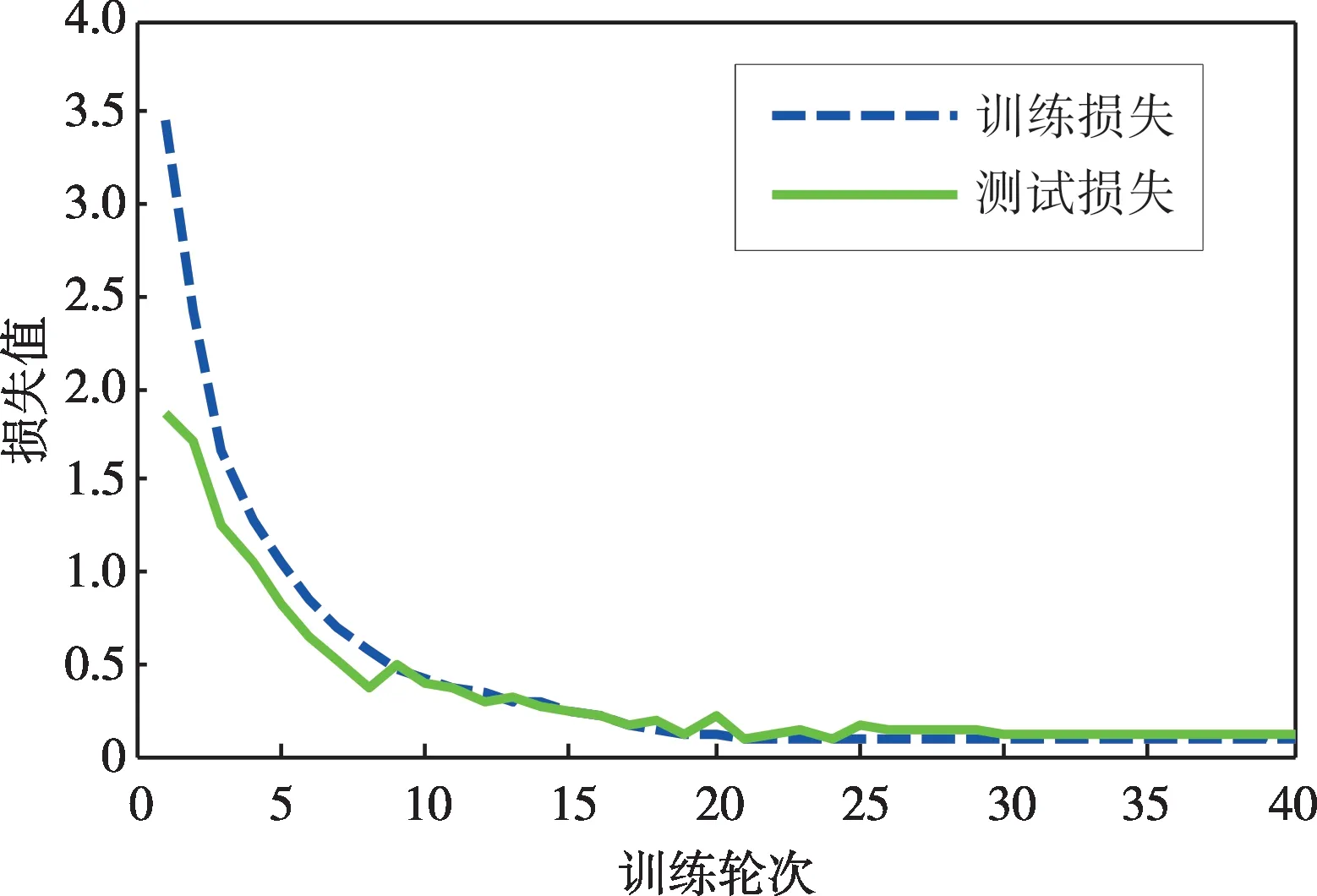
圖11 單一MobileNetv2網絡訓練及測試損失值

3.3 方法對比研究

為了驗證MSSST算法在分接開關振動信號時頻特征提取方面的優勢，分別利用MSSST、MSST、CWT、ST、STFT 和WVD 等時頻分析方法對分接開關正常及故障運行工況下拾取的樣本信號進行處理，并將所得時頻圖像輸入到RLCNN模型中進行測試。在參數相同條件下識別30 次來保障對比結果的準確性，所得結果如圖12及表3所示。其中利用MSSST算法提取樣本時頻特征后，RLCNN模型的平均識別準確率最高，達到99.32%，比MSST、CWT、ST、STFT、WVD算法分別高6.81%、12.18%、19.55%、22.93%、34.64%。此外，利用MSSST 算法進行時頻特征提取，RLCNN 模型30 次識別結果的標準差僅為0.359，均小于其他時頻分析算法識別結果的標準差，由此表明MSSST算法提取出的時頻特征更加穩定、魯棒性更佳。

表3 不同時頻分析方法準確率對比

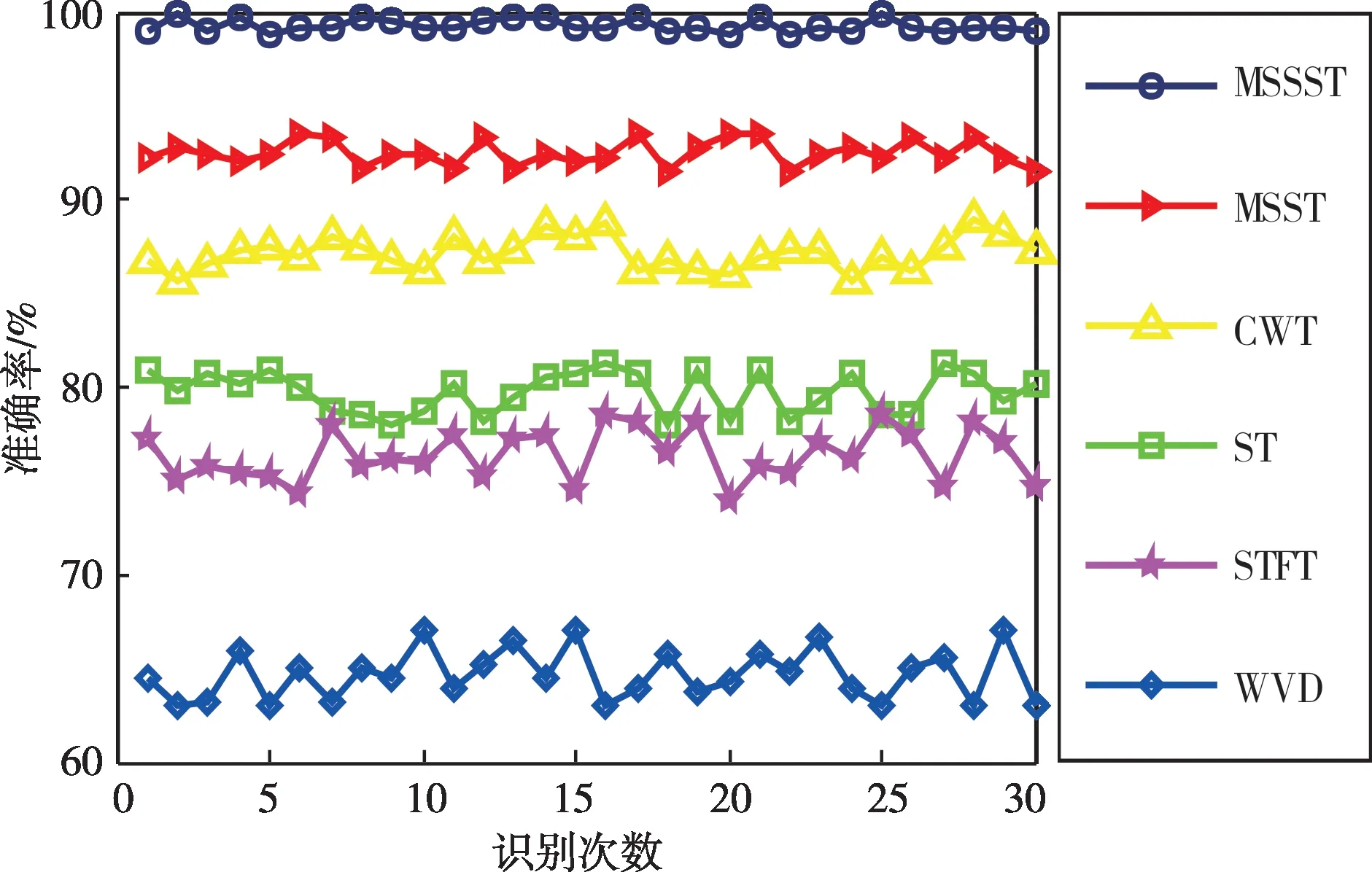
圖12 不同識別次數準確率對比

為了驗證本文所提有載分接開關工況識別方法的優越性，分別利用單一MobileNetv2 模型、CNN模型、ELM（極限學習機）［17］、SVM（支持向量機）［18］、BP（反向傳播）神經網絡［19］來識別分接開關的運行工況，設置5種對比方法與本文所提出的識別方法進行比較，見表4。與RLCNN模型相同，單一MobileNetv2 模型以及CNN 模型均可以直接從二維時頻圖像中自動提取特征信息，因此可將MSSST處理所得結果直接作為模型輸入，而傳統的ELM、SVM、BP 分類器則無法像深度學習網絡模型一樣自動讀取并捕捉二維時頻圖像的特征，需要人為干預構造合理的特征向量作為輸入才能夠對其進行訓練。在現有文獻報道中，多尺度熵算法已被大量用于描述信號動態特征，在電力設備狀態監測診斷領域具有諸多成功應用案例，并獲得了廣泛認可，因此本文計算有載分接開關不同運行工況下樣本信號的MPE（多尺度排列熵值）［20］作為ELM、SVM 和BP 模型的特征向量輸入。

表4 6種識別方法比較

在訓練集/測試集數量比為4∶1 條件下，即訓練集樣本1 600 個、測試集樣本400 個，分別利用6 種方法識別30 次并計算準確率均值，最終結果圖14所示。從圖中可以看出，本文提出的方法（方法1）識別準確率最高，達到99.35%，而方法2—6的識別準確率均值分別為94.76%、95.21%、89.34%、88.27%、84.63%，均低于本文所提方法。在訓練速度方面，RLCNN、MobileNetv2、CNN 深度學習模型內部包含大量的網絡參數，因此相比于傳統的ELM、SVM、BP 機器學習模型所需訓練時間明顯增多。需要指出的是，傳統CNN深度學習模型參數大小為550 MB，單一Mo?bileNetv2網絡模型參數大小僅為13.5 MB，而由5個單一MobileNetv2網絡所構造的RLCNN 模型參數大小也僅為67.5 MB，與傳統CNN 深度學習模型相比，在保證識別精度的前提下網絡規模明顯減小。當圖14 中的不同方法完成訓練后，應用于測試樣本識別時所需時間相差不大，以任意一個隨機樣本為例，分別利用方法1—6 對其工況進行識別，計算耗時分別為0.75 s、0.64 s、0.88 s、0.21 s、0.27 s、0.39 s，均能夠滿足實際工程現場需求，但是本文所提方法能夠獲得最高的識別精度。因此，綜合對比分析，本文提出的方法具有明顯優勢。

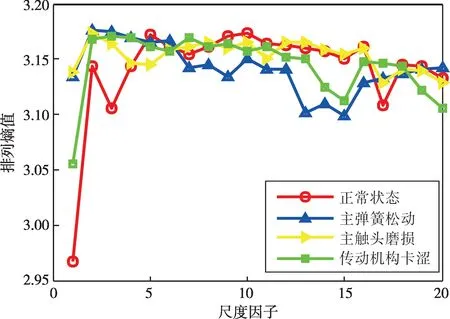
圖13 不同工況樣本MPE曲線

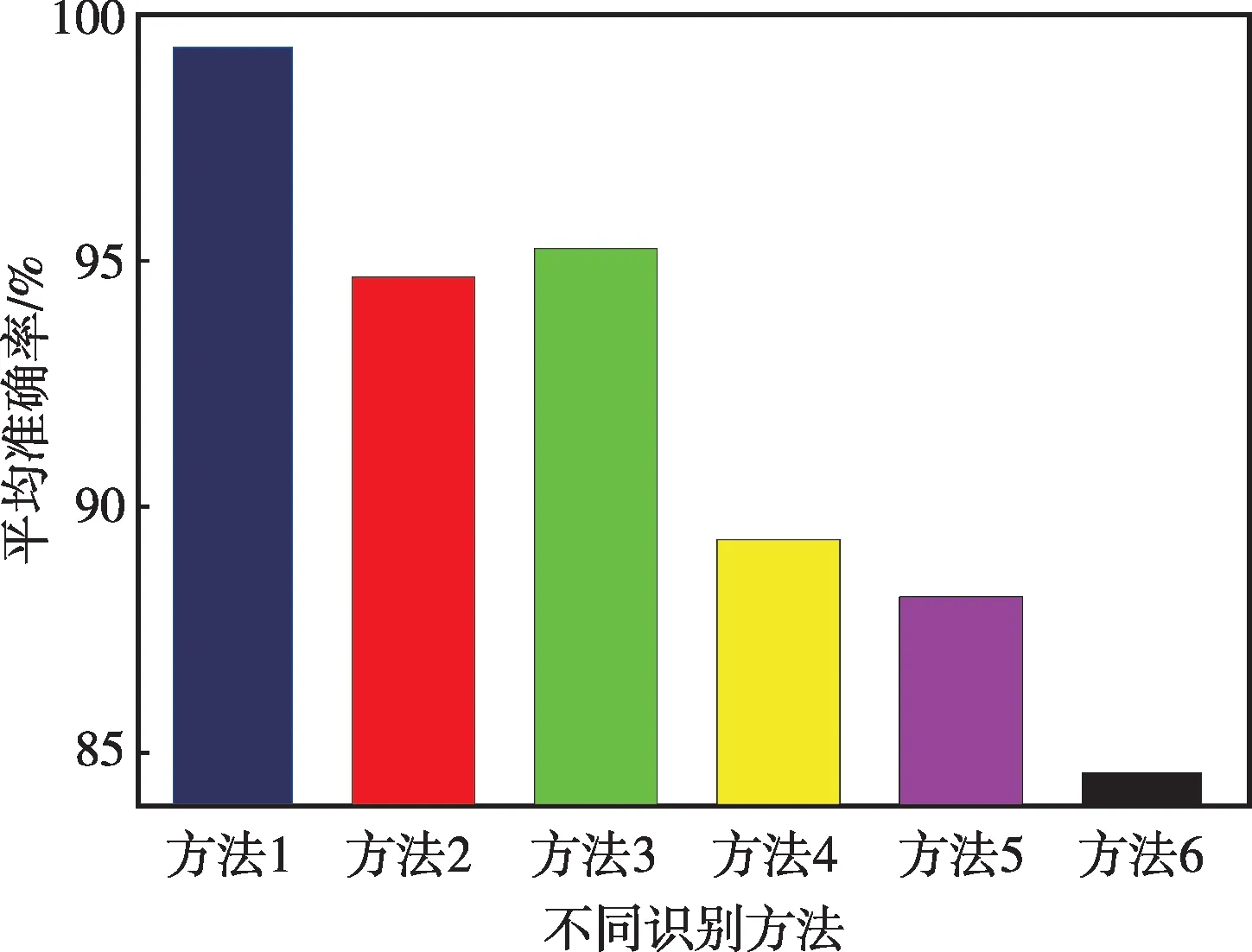
圖14 不同識別方法平均準確率

為了進一步驗證本文所提識別方法的穩定性，從2 000個樣本集中隨機抽取出不同數量的訓練樣本，針對分接開關4種運行工況狀態，分別組成數量比為3∶1、2∶1、1∶1、1∶2 的訓練集和測試集，如表5所示。利用表5中不同比例條件下的樣本集對圖14 中的6 種識別方法進行訓練及測試，所得平均準確率統計結果如表6所示。整體來看，無論在何種比例條件下，本文方法的識別準確率均優于其他對比方法。由表6的比較結果可以進一步看出，隨著訓練集樣本的減少，所有識別方法的平均識別準確率均有所下將，但本文方法的識別準確率并未像其他對比方法一樣出現顯著下降。即使在訓練集樣本數明顯小于測試集樣本數時（數量比為1∶2），本文方法的平均識別準確率仍能達到91.76%，而其他方法的平均準確率分別為82.38%、83.69%、76.51%、73.27%、61.87%，表明利用本文方法進行分接開關運行工況識別時，穩定性較好。究其主要原因在于以下兩個方面：MSSST時頻分析方法可以從原始振動信號中捕捉到敏感的差異性時頻特征，為后續模型的工況識別奠定了良好基礎；在MobileNetv2 網絡中引入了Ada?boost 自適應提升機制，該機制通過逐步構造更為困難的學習問題，能夠在少量有限數據集條件下有效實現模型的強化訓練，從而獲得更為強大的分類能力。

表5 不同比例的訓練集、測試集組成

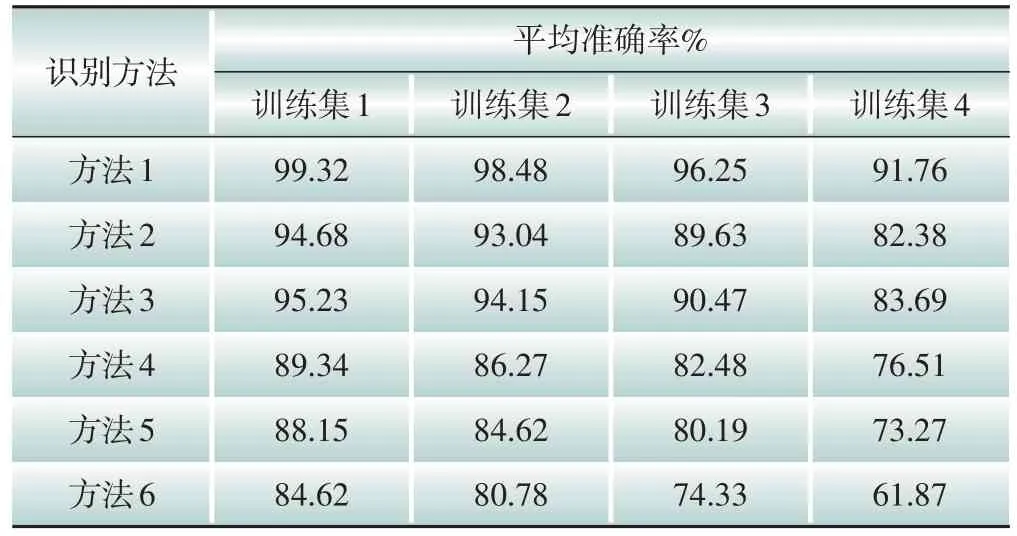
表6 不同識別方法下各訓練集平均準確率

4 結語

針對有載分接開關運行工況識別問題，本文提出一種基于MSSST和RLCNN的識別方法，所得結論如下：

1）利用MSSST算法對分接開關振動信號進行處理，能夠獲得比傳統時頻分析方法更為精細的時頻特征表達，有效提升樣本的特征維度，有利于實現分接開關運行工況的準確判定。

2）以多個MobileNetv2 輕量級CNN 作為基分類器，通過Adaboost 自適應提升機制對其進行強化學習訓練，并按不同權重進行組合，可構造出性能更為優越的RLCNN。

3）實驗結果表明，本文所提方法可自動實現分接開關多工況的準確辨識，與其他方法相比，識別準確率更高，穩定性更好，優勢更為明顯，具有一定的實際工程應用價值。

由于有載分接開關故障類型較多，在后續研究中將不斷積累構建其典型多樣性故障數據庫，用于強化完善本文所提方法的識別能力，提高變壓器有載分接開關的運行可靠性。