情景-應對模式下考慮軟時間窗的高鐵應急資源調度優化*

湯兆平，聶 欣，王振宇，孫劍萍

(華東交通大學 交通運輸工程學院，江西 南昌 330013)

0 引言

近年來，高速鐵路迅速發展，運輸里程占鐵路總里程的25.3%，客運量占鐵路總量64.4%[1]。高速鐵路具有運行速度快、運行密度大及長大隧道和高架多等特點，外加大量自主研發的新設備、新技術投入運用，使得高鐵突發事件呈現種類多、影響大的特征，給應急救援帶來新的挑戰。因此,研究應急資源快速、高效調配是提升高速鐵路應急處置水平的關鍵。

部分學者針對突發事件應急資源的調配優化進行研究，并取得一定成果。耗時最少是指整個配送任務的時間最短，是應急資源調度考慮的核心因素。在考慮救援時間最優條件下，還應考慮出動規模及救援成本等其他因素，因此學者將最小費用[2]、救援公平性[3-4]等影響因素納入考慮范圍，構成多目標決策模型，以解決最優化應急調度問題，提升應急資源調度能力。

突發事件的不可預測性、突發性,以及信息獲取的缺失性和多變性，導致應急管理決策主體缺乏足夠準確的信息來制定救援方案，使鐵路應急救援過程中參數(如各事故點資源需求量、資源調度時間、救援成本等)存在不確定性。學者從需求不確定性、災情動態變化、災情情景分析等方面對資源調度進行研究：Liu等[5]針對需求和運輸時間的不確定性，考慮山區災后抗震救災過程中特殊環境條件，提出災后抗震救災物流隨機模型；湯兆平等[6]針對鐵路突發事件發生后應急資源的不確定性，通過比較模糊評價和熵權的灰色關聯理想法，得出受災點的救援優先級；王飛躍等[7]引入區間數描述物資需求量和物資運輸時間的不確定性，并以應急物資分配的經濟性、時效性和公平性為目標，建立多目標線性區間規劃模型；Sun等[8]為研究救援效率最高和事故損失最小，考慮需求的不確定性，提出救援決策響應時間最優的雙目標魯棒優化模型；任斌等[9]運用前景理論研究需求不確定性問題，構建應急物資需求動態調整模型，以保障應急資源需求預測的合理性。

現有文獻大多針對公共突發事件的應急資源調度優化問題進行研究，部分針對鐵路突發事件應急資源調度優化問題進行討論，卻忽略高鐵運行環境特點、突發事件特點及應急情景的分析。本文考慮高速鐵路突發事件發生后應急資源需求的不確定性，以“情景-應對”模式為基礎，通過對事故情景集進行分析計算，預測得到應急資源需求量，引入“軟時間窗”概念，構建以超時懲罰成本、資源運輸成本和救援點固定出動成本3者之和最小化為優化目標的應急資源調度模型，為高鐵應急救援部門的科學、高效決策提供理論依據。

1 高鐵突發事件情景分析

情景分析是基于未來事件的不確定性無法避免，但未來事件的某些方面是可預測的[10]。在應急管理領域，情景分析可作為評估應急資源需求以及確定應急資源配置和調度的基礎。

1.1 “情景-應對”模式下高鐵應急處置流程

“情景-應對”模式的思路是通過改變情景集中的要素值實現情景變化，根據突發事件具體情景信息進行相似度計算，為優化決策提供重要參數。具體應急處置過程包括事件報告、情景要素分析、相似度計算、情景應對學習、資源調度優化以及應急終止，如圖1所示。

圖1 “情景-應對”模式下的高鐵應急處置流程Fig.1 High-speed rail emergency response process under the “scenario-response” model

1.2 高鐵突發事件情景要素提取與分析

情景要素作為“情景-應對”模式研究的重要基礎，合適與否直接關系情景集的實用價值。高速鐵路特征主要表現為客運列車運行密集、列車速度快和高架線路及長大隧道多，需要重點分析乘客要素、天氣環境和地理環境要素。此外，需要對設備的相關要素進行提取。本文根據高鐵突發事件特點和發生機理，將情景集要素分為2級，1級要素包括事件、乘客、設備等7種類型；2級要素包括事件名稱、事故類型、受傷人數等26種具體指標。

情景集表示采用三元組表達式進行描述，如式(1)所示：

Scenario(F，M，U)

(1)

式中：F表示情景集的2級情景要素；M表示應急解決方案情景要素；U表示執行解決方案后的效果情景要素。

1.3 突發事件情景要素相似度計算

目標情景與當前情景相似度主要考慮情景要素的局部相似度和情景的全局相似度2方面。其中，局部相似度利用不同算法對所包含的枚舉型、數值型、區間型、字符型和模糊型要素進行相似度計算；全局相似度考慮要素值完全和要素值不完全2種情況。

1)枚舉型要素。包括事件類型、事件原因、事故響應等級、列車種類、天氣、事故地點、資源類型等2級要素，當2個要素值相同時取其相似度為1，反之為0，如式(2)所示：

(2)

式中：Tf為目標情景第f個2級要素的值；Cmf為第m個情景中第f個2級要素的值。

2)數值型要素。包含事件時間、經濟損失、受影響乘客數量、脫軌車廂數、列車脫軌最遠距離等2級要素，此類要素采用基于海明距離公式[10]計算屬性間的相似度，如式(3)所示：

(3)

式中：δ，λ分別為情景集中要素f取值范圍的最大值和最小值。

3)字符型要素。包括事件名稱、救援方案、存儲位置等通過字符串進行描述的要素。假設Ωf={ε1,ε2,…,εu}，Ωmf={γ1,γ2,…,γv}為2個不同情景要素的集合表示，則Ωf與Ωmf之間的相似度定義如式(4)所示：

(4)

4)區間型要素。高鐵突發事件發生后，受災點的旅客傷亡人數、車輛脫軌數等受災信息無法得到準確數值，只能得到1個區間值，用式(5)計算數值和區間數之間的相似度：

(5)

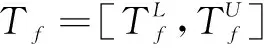
5)模糊型要素。利用三角模糊數表示模糊型要素，并采用Wasserstein距離式演化的方法[11]計算相似度，如式(6)所示：

(6)

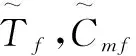
6)情景全局相似度計算。情景全局相似度計算建立在局部相似度計算基礎之上。根據數據類型多樣、部分數據缺失等實際問題，需要先通過比較情景之間所包含的情景要素，對其結構相似度進行計算。情景T與Cm之間結構相似度計算主要包括以下4個步驟：①情景T與Cm的所有非空集合分別記為ΩT和ΩCm。②ΩT和ΩCm的交集為Ω1=ΩT∩ΩCm和并集為Ω2=ΩT∪ΩCm。③將各要素權重值累加計算得到交集Ω1和并集Ω2所有要素的權重之和分別為WΩ1和WΩ2。④情景T與Cm的結構相似度計算如式(7)所示：

(7)

計算2個情景之間的全局相似度，需要綜合考慮2者之間的結構與要素相似度，借鑒結構相似度算法[12]得到全局相似度計算公式，如式(8)所示：

(8)

式中：sim(T,Cm)為情景集中的情景T與目情景Cm的總體相似度值；?c為第c個1級要素的權重；sim(Tf,Ccf)為目標情景T的1級要素c下第f個2級要素與情景集中C情景的1級要素c下第f個2級要素的局部相似度；?cf為1級要素c下第f個2級要素指標權重；N為1級要素的個數；Mc為1級要素c下2級要素個數。

1.4 情景-應對下資源需求量的預測

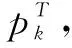
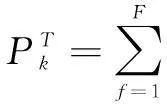
(9)

式中：Xk為源情景中k類資源的需求量；sim(Tf,Cf)為情景T與源情景第f個元素相似度。

2 情景-應對模式下應急調度模型構建

2.1 模型假設

情景-應對模式下應急調度模型構建需要作如下3個假設：

1)已知突發事件的受災點位置、備選救援點位置及資源存儲量。

2)假設最佳救援時間為90 min內。

3)救援點出動時間為30 min，救援列車按規定速度勻速行駛至受災點。

2.2 模型基礎

模型中{S1,S2,…,Si}為備選救援點集合，i∈I；E為受災點；K為救援點應急資源類型集合，k∈K。模型參數及其定義見表1。

表1 模型參數及其定義Table 1 Parameters and definitions of model

2.3 模型建立

高鐵突發事件發生后，時間成為應急救援的關鍵因素。在以往研究中，學者引用“硬時間窗”對時間進行約束，即一定要在規定時間內到達，否則視為無效救援。但在實際救援中，應急資源的送達可能會超過預測時間窗限制。為解決“硬時間窗”的不足，本文引入“軟時間窗”表達救援超時的懲罰成本。

“軟時間窗”指因超出規定服務時間會產生相應的懲罰，但依然需要對客戶進行服務，懲罰成本為遲到時間與懲罰系數之積[13]。選用升半柯西函數作為“軟時間窗”的懲罰函數，如式(10)所示：

(10)

式中：α、β均為懲罰函數系數。

在實際救援中，應急資源不受限制的配置和調度會造成浪費[14]。為研究應急調度中時間和效益的問題，構建超時懲罰成本、資源運輸成本和救援點固定出動成本3者之和最小化模型，如式(11)～(18)所示：

(11)

(12)

(13)

(14)

(15)

(16)

Δti≥0i∈I

(17)

(18)

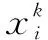
3 算例驗證

以某高鐵列車事故為例，事故造成現場線路中斷，列車和線路設備遭到破壞，需要調度應急物資進行緊急救援及搶修。C={C1,C2,C3,C4,C5}為情景集中已知的5個源情景。源情景數據通過國內外歷年鐵路運營事故數據，并篩選國內外高鐵客運事故案例得到，個別事故源情景選取與高鐵運行環境相似的鐵路旅客列車運行事故。當前事件為情景T，通過對事故現場基本信息進行總結分析，選取權重相對最高的16個2級要素作為決策參考，見表2。

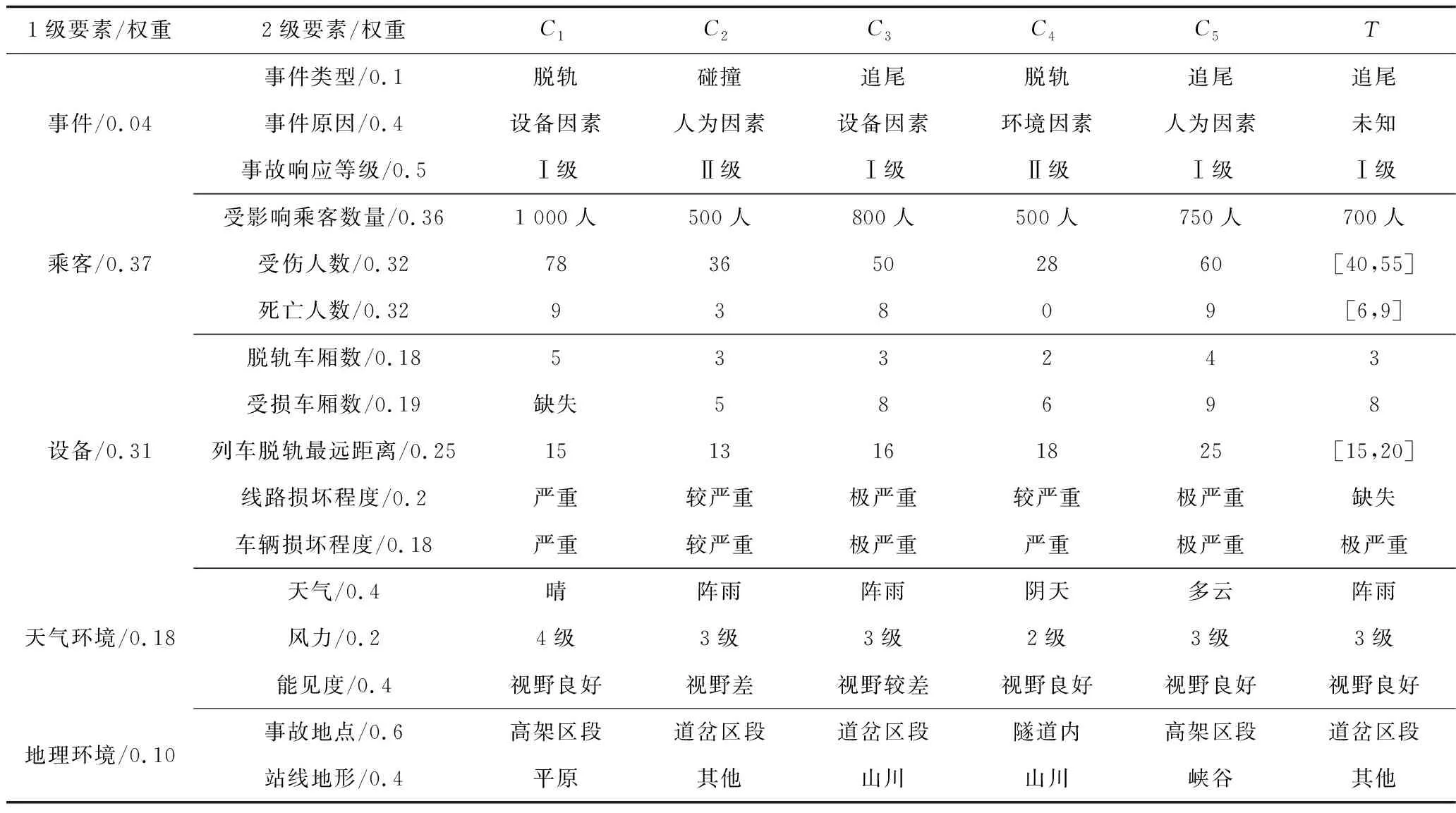
表2 情景要素取值Table 2 Scenario elements value table

利用層次分析法計算情景要素權重。參考相關文獻[11,14]以及通過專家座談會確定的各級情景要素，選取事故情景的5個1級要素即事件、乘客、設備、天氣環境及地理環境，對各要素進行兩兩比較打分。邀請20名具有10 a以上相關工作經歷的中級以上職稱專家，及相關高校的專業技術人員對以上各情景要素進行權重值評價。5個1級要素的權重見表3，同理求得各2級要素權重。

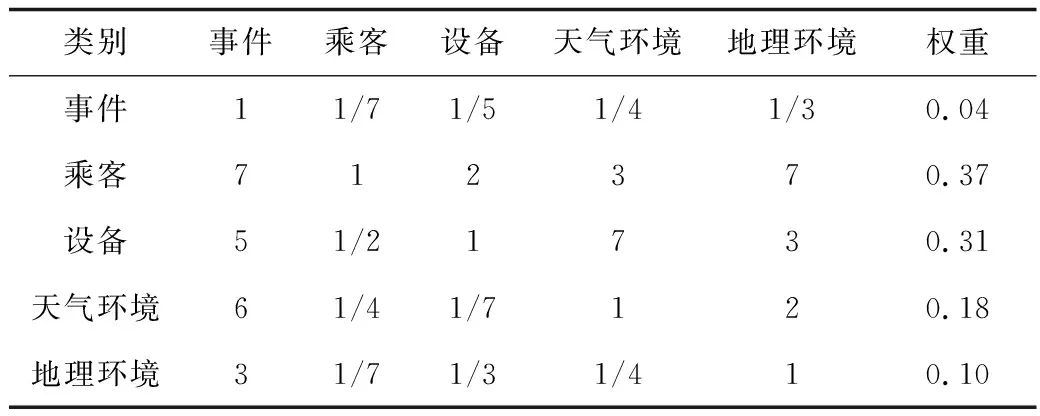
表3 情景要素判斷矩陣Table 3 Situational elements judgment matrix

建立情景要素判斷矩陣，求得最大特征根λmax=5.43。將λmax=5.43、r=5和RI=1.12代入式(19)中計算，求得判斷矩陣一致性比率CR=0.097<0.1，判斷矩陣滿足一致性檢驗：

(19)

式中：λmax為判斷矩陣的最大特征根；r為矩陣階數；RI為隨機一致性指標，r=5時，查表得RI=1.12。

根據式(1)～(6)，計算得到目標情景與情景集中各情景之間2級要素相似度，通過式(7)～(8)計算情景全局相似度見表4。

表4 T與情景集C的全局相似度Table 4 Global similarity between T and situation set C

由表4可知，C3與目標情景的相似度最高為0.87。因此，根據C3中的應急資源類型和數量對情景T的應急資源量進行預測。為驗證情景預測方法的可行性，獲取目標情景T的實際應急資源類型及數量，將實際使用量與各情景預測量對比。情景預測值在目標情景中的對比見表5。由表5可知，情景C3的應急資源使用量預測值更接近當前情景T的實際使用量(與其他情景的需求預測的平均誤差比值相比分別降低了12.10%、10.66%、16.75%、10.30%)，能夠更準確預測出當前情景的應急資源需求，可為后續應急資源調度提供支撐。

表5 情景預測值在目標情景中的對比值Table 5 The ratio of the scenario predicted value in the target scenario

根據情景提取，受災點所需的應急資源為軌道起重機、復軌器、食物飲用水、發電機組和急救車5種。救援點S1，S2，S3，S4，S5為受災點提供應急資源，其中S1為1級救援點，其他為2級救援點。表6～9為情景T的具體信息。

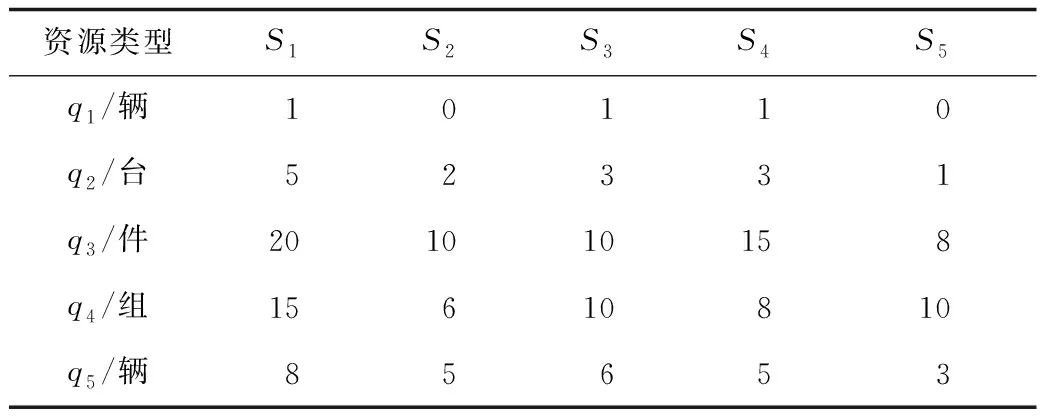
表6 救援點Si的物資擁有量Table 6 Material possession of rescue point Si

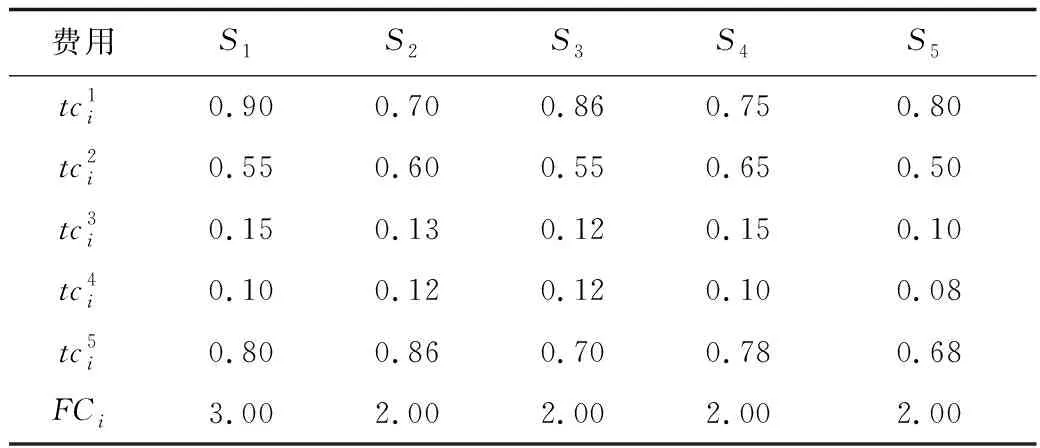
表7 救援點Si到受災點E的救援費用Table 7 Rescue cost table from rescue point Si to demand point E 萬元

表8 受災點E的物資需求Table 8 Material requirements table for disaster-affected point E

表9 救援點Si到受災點E的距離Table 9 Distance and time from rescue point Si to demand point E

設置“軟時間窗”函數中的系數α、β均為2，通過Matlab軟件運用遺傳算法求解模型。經過多次運行實驗比較后，設置初始種群個體數目為30，迭代次數為200，交叉概率為0.7，變異概率為0.02。從結果中選取10組Pareto最優解做進一步分析。

為保證結果分析的有效性，對目標函數參數進行歸一化[15]。采用式(20)對目標函數值進行歸一化處理，得到Pareto最優解目標函數值：

(20)

式中：Z*為歸一化后的目標函數值；Z為歸一化前的目標函數值;Zmax為Pareto解群中的最大值；Zmin為Pareto解群中的最小值。

建立單目標函數的表達式，將歸一化后的函數值通過式(21)計算得到最終優化結果：

(21)

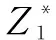
模型中2個子目標體現 “時間”與“效益”的關系，在實際救援中，需要找到2者的相對平衡。根據幾種典型的權重系數對函數值進行計算，結果見表10。

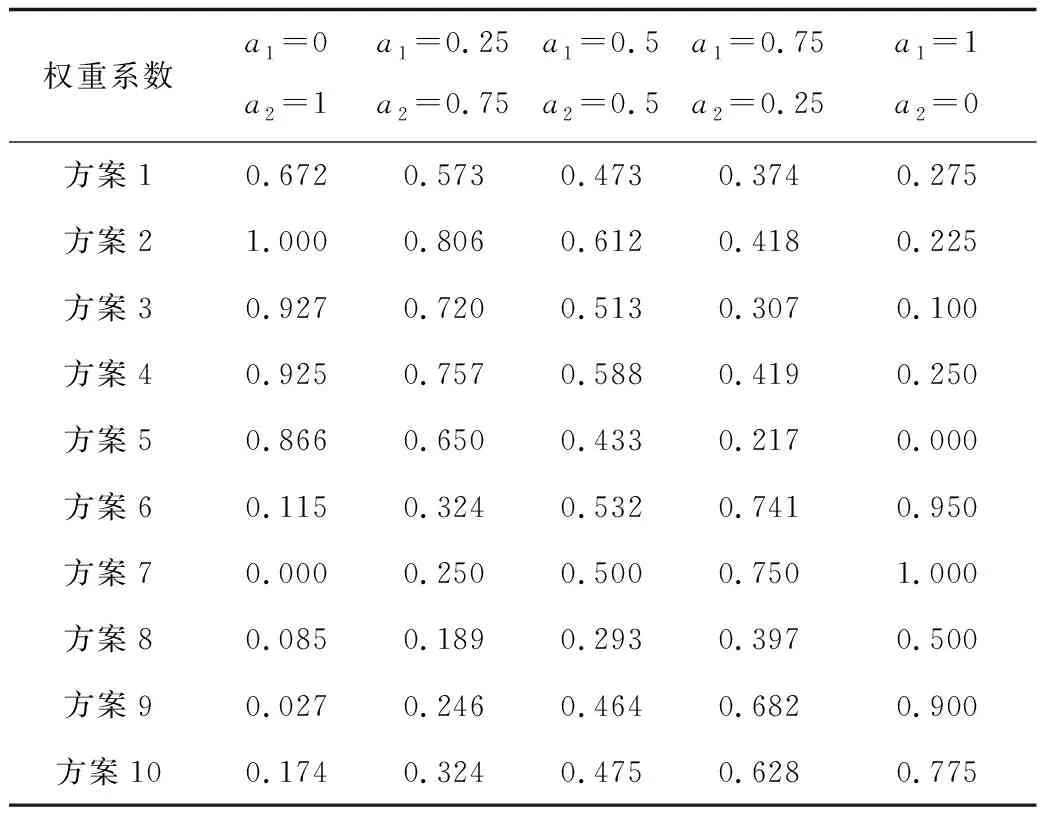
表10 幾種典型權重系數下Pareto最優加權結果Table 10 Pareto optimal weighting results under several typical weighting coefficients

由表10可知，遺傳算法具有很強的魯棒性和全局尋優能力，適合求解復雜的多極值優化問題和組合問題，具有求解速度快、獲得的Pareto最優解不唯一等特點。所得Pareto最優解群可針對不同決策側重點，設置子目標函數參數權重，利用歸一化的方法進行計算分析，選擇最適合的方案，為應急資源調度提供科學的依據。

為驗證方法可靠性，選取a1=0.25，a2=0.75，利用Matlab調用Cplex求解器對模型進行求解比較，Cplex求得結果為34.5萬元，遺傳算法求解得到的Pareto最優解為30.5萬元。結果表明，遺傳算法對非線性優化模型求解效率更高，所得結果節約4萬元，驗證方法的有效性。

4 結論

1)通過建立高鐵突發事件的多級情景要素體系，對高鐵突發事件進行特征要素分析，得到相似度最高的源情景作為參考，從而將不確定的資源需求量轉化為可預測值。實例驗證中情景總相似度最高可達87%，為當前事故情景提供可靠的決策參考。

2)利用“情景-應對”模式預測得到應急資源需求量，確定優化目標并構建調度優化模型，滿足高鐵應急調度的及時性和經濟性。通過改變子目標的權重值適應不同的決策偏好，對高鐵應急救援工作有很強的借鑒意義。

3)由于資料收集限制，情景庫中源情景較少，導致模型精度不高，下一步研究中需要進一步收集事故情景，豐富情景庫數據。