基于反賦權與MBCT-SR多維云模型算法巖爆預測研究*

宋英華，龐昭勝，李墨瀟，江 晨，齊 石

(1.武漢理工大學 中國應急管理研究中心，湖北 武漢 430070；2.武漢理工大學 安全科學與應急管理學院，湖北 武漢 430070)

0 引言

巖爆是堅硬巖石開采和土木建筑中最常見的由連續巖體應力過大引起的破壞之一，其發生總是伴隨著巖塊開裂、剝落、拋擲、巨響等現象[1]。巖爆具有突發性、破壞性強、難控制等特點，極易對現場施工人員及工程設備造成損傷[2]。隨著地下巖體開采深度和挖掘需求的增加，巖爆事故的發生頻率與影響程度也越來越嚴重，巖爆已成為愈發被重視的工程問題。

由于巖爆機理的復雜性，且各指標數據測取具有較大的不穩定性，巖爆分類預測在世界范圍內都一直是迫切需要解決的難題，巖爆烈度等級評價研究主要有3大類[3]：1)第1類是基于巖爆機理判據，如應力強度Russense判據、Barton判據，能量理論中能量比指標判據等直接進行評價；2)第2類則需要對巖爆現場進行實測，諸如微震法、聲發射法等；3)第3類是基于巖爆影響因素的綜合預測方法，是目前巖爆預測研究的熱點。第3類方法又有2種不同的判別方式，一是基于巖爆工程實例數據，如采用XGBoost[4]、神經網絡[5]、隨機森林[6]等機器學習模型進行評判；二是基于巖爆指標判據的預測方法，主要運用模糊綜合評判模型[7]，理想點模型[8]，云模型[9]等進行預測。

針對巖爆的隨機性和模糊性特點，云模型的使用在巖爆預測中成為當下研究熱點，已被證明具有一定的可靠性。Liu等[10]將云模型與粗糙集理論進行結合，根據沖擊地壓標準生成正態云模型，運用粗糙集理論確定權重，最后利用最大隸屬度原理確定巖爆等級；周東良等[11]引進改進的AHP、熵權法、博弈論和模糊熵理論組合賦權法與二維云模型綜合評判；劉曉悅等[12]將指標的權重融合到多維云模型中，生成多指標的等級綜合云進行預測并驗證了模型的可靠性及實用性。目前，云模型在巖爆預測方面的研究中，大多學者都采用正態云模型的正向云發生器算法，而正向云發生器算法的數字特征一般是經驗值，往往具有較強的主觀性。逆向云發生器算法是基于數據生成數字特征，具有較強的客觀性，在巖爆預測研究中的使用較少。由于巖爆災害等級確定受多指標綜合影響，多維云模型也應運而生。多維云模型的權重分配研究目前大多是依靠主觀賦權與客觀賦權相結合的方式，但此類方式往往面臨著主觀權重的精度以及權重結合方法的科學性不足等問題，使問題復雜化。

本文采用逆向云發生器MBCT-SR算法[13]，解決確定云模型數字特征及權重時，由于主觀干擾導致的預測結果與實際情況存在偏差等問題，該算法基于一定數量的樣本實例，計算客觀云數字特征，并結合多維云模型建立動態適應度函數，通過改進的遺傳算法反求最優權重，從而建立完整的巖爆預測云模型，為巖爆預測研究提供更貼合實際案例數據的評價方法，使評價結果更加客觀準確。

1 巖爆預測多維云模型

1.1 多維正態云模型

正態云模型[14](圖1)可實現定性概念與定量表示的相互轉換，反映定性概念的不確定性，其性質通過期望Ex、熵En以及超熵He3個數字特征表示。其中期望Ex為云的重心，最能代表定性概念；熵En表示定性概念的離散程度；超熵He則表示熵的離散程度，是熵的不確定性度量。

圖1 云的數字特征Fig.1 Digital features of cloud model

在一維正態云模型的基礎上，引入精確數值表示的n維集合U={X1,X2,X3,…,Xn}，其中U為n維定量論域，C為U上一定性概念。對于U中任意值X=(x1,x2,x3,…,xn)(X∈U)，都存在X對U有一定約束的隨機數μ(X(x1,x2,x3,…,xn))，稱為確定度。多維正態云模型確定度式[15]為式(1)：

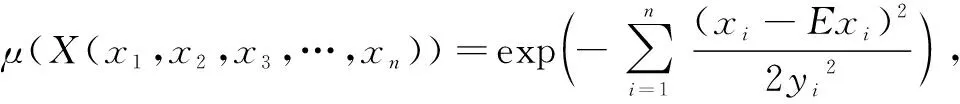
(1)

式中：i表示n維數據中第i維數據(i=1,2,3,…,n)；yi為服從以熵Eni為均值，超熵的平方Hei2為方差的正態分布隨機數；xi滿足以期望Exi為均值；yi為方差的正態分布規律。

多維云模型包含2種云發生器，一種是正向云發生器(CGn)，另一種為逆向云發生器(CGn-1)，2種發生器可進行雙向轉換，如圖2所示。

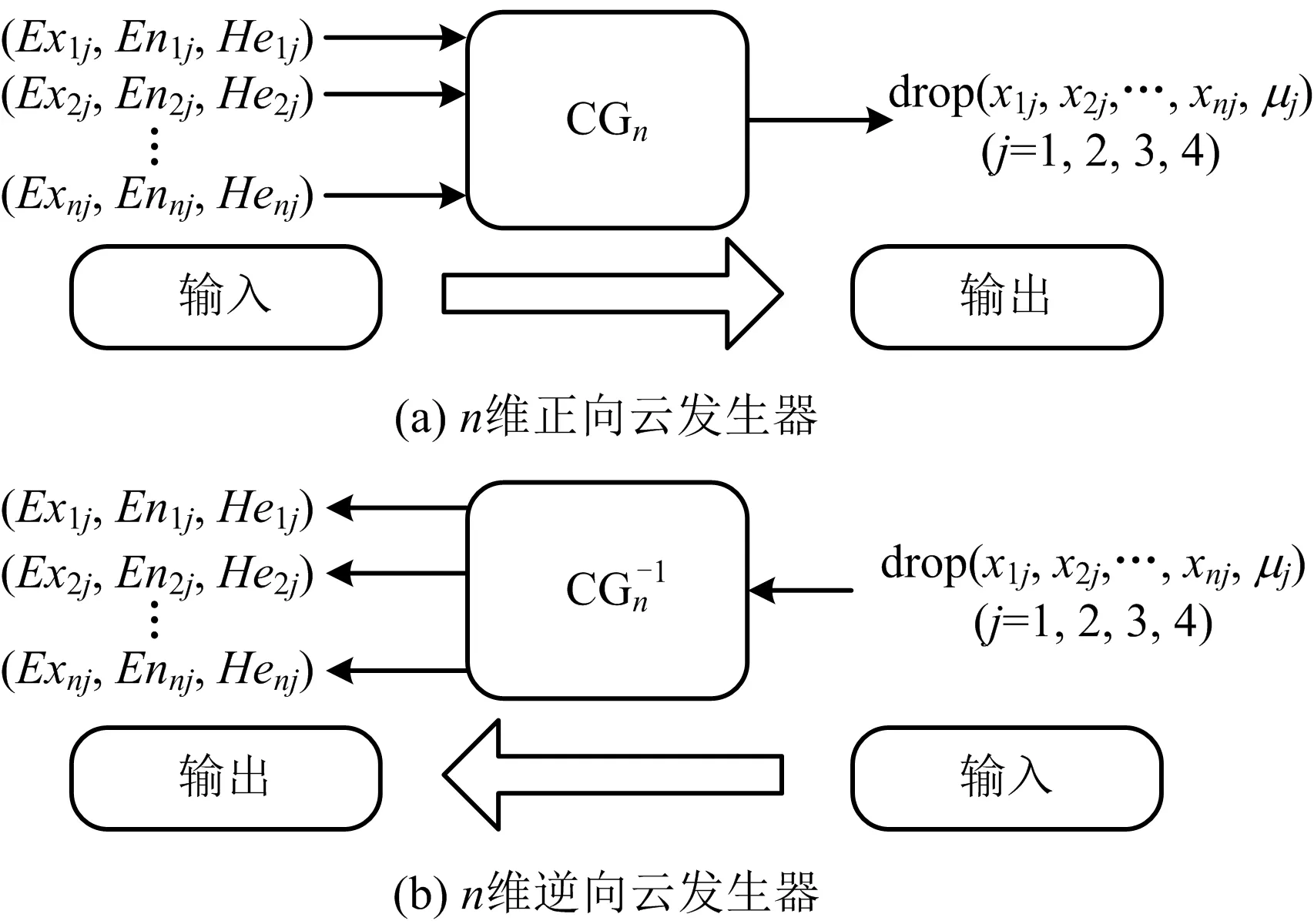
圖2 多維云發生器Fig.2 Multi-dimensional cloud generator

n維正向云發生器是指將定性概念通過n組數字特征N(Exn,Enn,Hen)表示，并生成一定數量的云滴P(X(x1,x2,x3,…,xn))，μj的過程，公式(1)中用j來表示巖爆等級序列(j=1,2,3,4)；逆向云發生器是指基于一定數量的云滴，計算云數字特征的過程，在云滴較少的情況下數字特征一般為估計值。

1.2 MBCT-SR算法及綜合確定度

通過式(1)可知數字特征決定確定度的取值及其波動范圍，傳統云模型數值特征一般采用經驗式[16]進行計算，即式(2)：

(2)

式中：各指標上下限Cmax、Cmin和固定值K均為經驗常數，這使得云模型規避了巖爆預測的模糊性特征，導致主觀性較強。云模型的逆向云發生器算法基于大量云滴數據，客觀計算云模型數字特征，減小經驗常數的主觀性。但傳統的SBCT-1stM逆向算法常伴隨計算結果漂移及不穩定等現象，因此，本文采用多步還原的逆向云變換MBCT-SR算法，提高結果的準確度和穩定性。具體算法步驟如下：

Step 1：輸入m個樣本點xk，k表示m個樣本點中所取樣本序列(k=1,2,3,…,m)。

Step 2：計算樣本均值，得到期望Ex的估計值，即

(3)

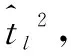
(4)

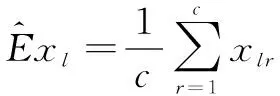
Step 4：將Step 3中的結果代入式(5)計算出En2與He2的估計值，即式(5)：

(5)

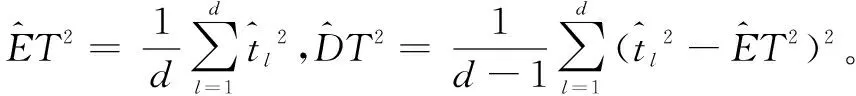
多維模型的建立需結合各指標權重，由式(6)計算綜合確定度Ω[17]，其中i為n維各項數據序列(i=1,2,3,…,n)，最終達到預測的目的。

(6)

2 指標權重反分析

依據文獻收集[3,6,11,12,16-18]的真實樣本數據192組，采用遺傳算法對指標權重進行反分析。設指標權重為未知變量，以最大化滿足樣本數據為結果，通過優化算法求全局最優解。具體流程見圖3。此方法降低權重確定主觀性，其分析步驟為：①確定評價指標；②收集樣本實例并進行數據預處理；③計算數字特征，構建多維云模型；④由式(6)，建立優化適應度函數；⑤利用遺傳算法，尋求全局最優解；⑥回代，驗證完整多維云模型的有效性及可行性。

圖3 指標權重反分析方法流程Fig.3 Flow chart of index weight back analysis method

遺傳算法只能從適應度函數中獲取信息，故步驟④為反求權重的核心內容，在求取適應度函數時，由式(6)可得綜合確定度中的參數yi為服從以熵Eni為均值，超熵的平方Hei2為方差的正態分布隨機數(i=1,2,3,…,n)，故yi需由MBCT-SR算法計算獲得其正態分布均值與方差，再進行隨機取值，最終建立動態適應度函數fitness[18]如式(7)：

(7)

式中：j為巖爆等級序列；i為評價指標序列；k為樣本序號；Ωj為第j個巖爆等級的綜合確定度；n，p，m分別為指標總數、巖爆等級總數和樣本總數；qk與Qk分別是第k個樣本中的預測等級和實際等級。

由式(7)可知，優化算法以預測結果滿足實例結果最大化為目標，規避主觀干擾，建立適應度函數，求出最優權重。求得權重代入式(6)，根據綜合確定度獲得最終評價結果。

3 模型實例驗證

3.1 評價指標選取及數據預處理

巖爆等級受多因素綜合影響，本文基于真實數據分析，規避主觀因素，對數據樣本具有較高的要求，數據精度直接影響預測結果。結合以往研究經驗，通過文獻收集[3,6,11,12,16-21]的方法，最終確定數據樣本較多、影響程度較大的3項指標：應力比Ts=σθ/σt、巖石脆性指數B=σc/σt以及彈性應變儲能指數Wet作為巖爆等級預測評價指標，參考王元漢等[22]的相關研究，巖爆等級依托于各指標分為無巖爆(Ⅰ)、輕微巖爆(Ⅱ)、中等巖爆(Ⅲ)、強巖爆(Ⅳ)4個等級評價。

本文研究數據樣本較全，不存在數據缺失的情況，但數據收集時無法避免存在噪點的情況出現。因此采用偏差分析結合箱線圖進行預處理，采用aσ(a=2或3)規則[23]進行修剪，其中σ表示原始數據方差，a表示以a倍方差為臨界值對離散數據進行截取。最終選取192 組國內外實際案例進行預測，其分布規律如圖4所示。

圖4 原始數據樣本箱線Fig.4 Box line diagram of original data sample

從圖4所知，由于各指標量綱不同，各指標數值差異較大，不利于進行科學計算及綜合分析，故按式(8)對各指標進行歸一化處理，即得

(8)

式中：xik為第i個指標中第k個原始樣本數據；ximin，ximax分別是第i個指標中原始樣本的最小值和最大值。

式(8)中原始數據歸一化后其分布結果如圖5所示。由圖5可得，預測指標巖石脆性指數B=σc/σt依舊存在一定數量的離散點，數據中心偏移較為嚴重，而應力比Ts=σθ/σt以及彈性應變儲能指數Wet分布較為均勻。指標上下四分位數跨度較小，其中Ts下四分位偏低，中位數靠近0.5，無離散點。彈性應變儲能指數Wet上四分位數偏高，中位數稍低，但總體分布比較合理。由歸一化數據分析初步猜測，本數據樣本指標B穩定性較差，權重應最小，這也滿足巖爆各指標權重分配的主觀認知。

圖5 歸一化后樣本箱線Fig.5 Normalized sample box plot

選取29組國內外實例數據做測試集，列舉部分如表1所示，以剩余163組數據為訓練樣本，并與其他云模型預測方法對比，驗證其準確性。

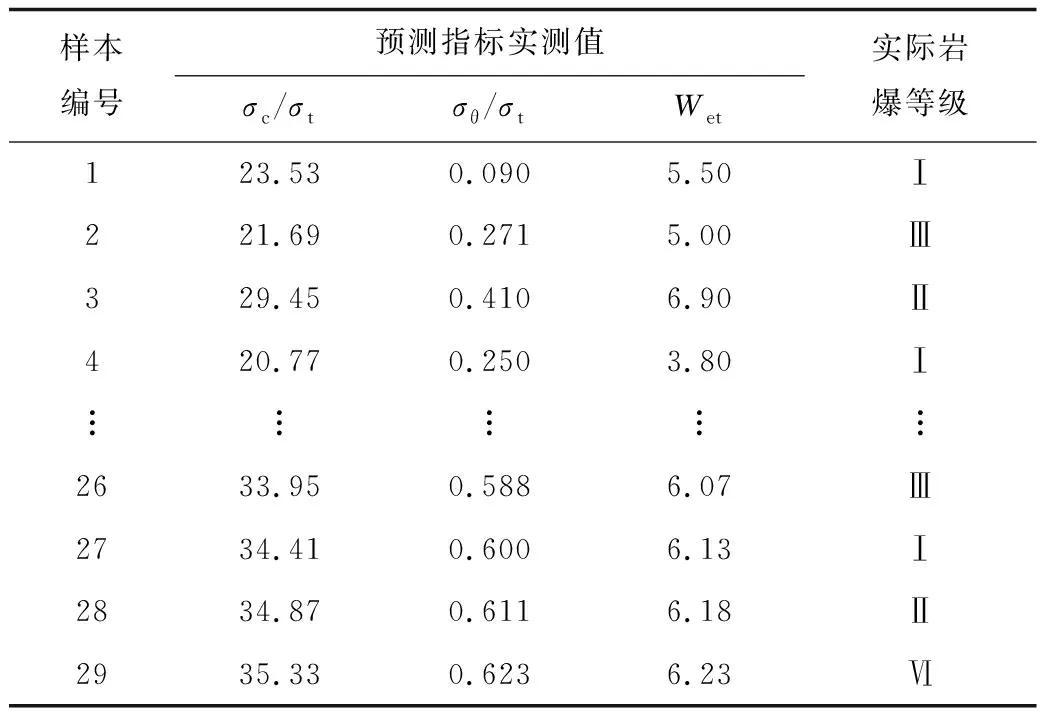
表1 國內外巖爆實例數據Table 1 Data of rock burst cases at home and abroad

3.2 計算數值特征

將163 組巖爆實例數據按級分類，并采用MBCT-SR算法對各級各指標巖爆數據分別計算，由于算法計算結果并不唯一，任選其一組將各數字特征示于表2 。

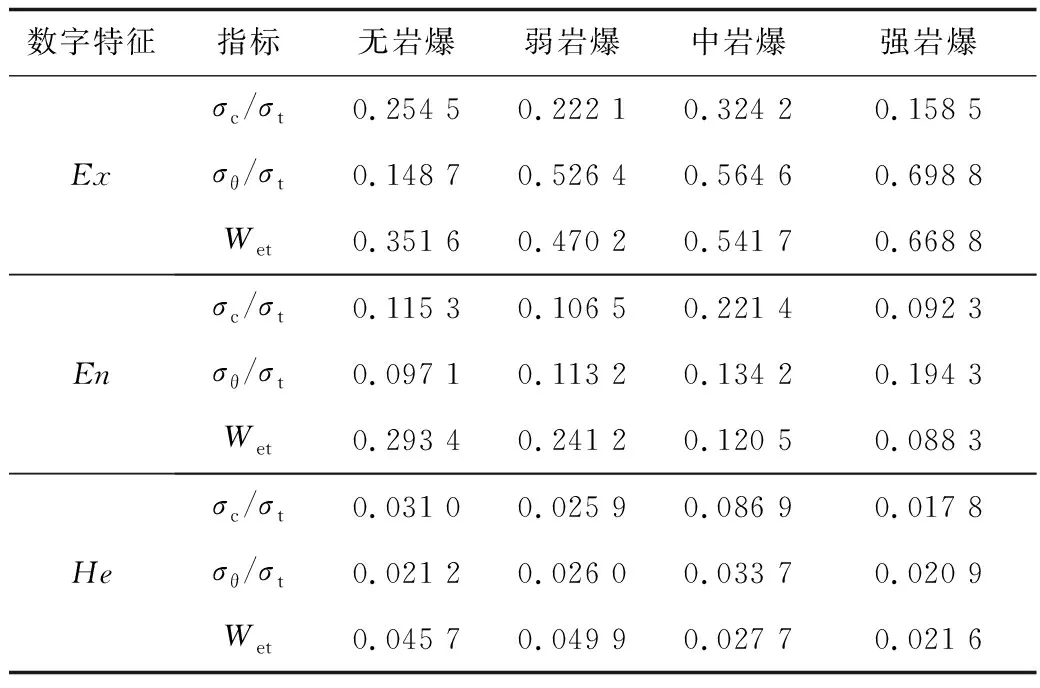
表2 數字特征計算結果Table 2 Digital feature calculation results

根據表2中各數字特征繪制多維云模型，如圖6所示。從圖6所知，“·”描繪數據代表無巖爆(Ⅰ級)，“+”描繪數據點代表弱巖爆(Ⅱ級)，“○”點代表中巖爆(Ⅲ級)，“*”點表示強巖爆(Ⅳ級)。指標Ts與實際巖爆順序相同，相對于其他2個指標分布較為均勻，各等級界限較為明顯。指標Wet的分布順序與巖爆順序也相同，但在無巖爆與弱巖爆中數據跨度較大，其分布特征相比于指標Ts較不穩定。B維度數據點分布順序較亂，跨度較大，很明顯相對于其他2指標規律性較差，最不適用于巖爆評價。此次MBCT-SR算法基于大量樣本數據計算數字特征并生成三維云圖的分析中，對第3.1節中假設進行了初步驗證，并針對圖6 做進一步假設，求得最終權重順序應滿足ωTs>ωWet>ωB。

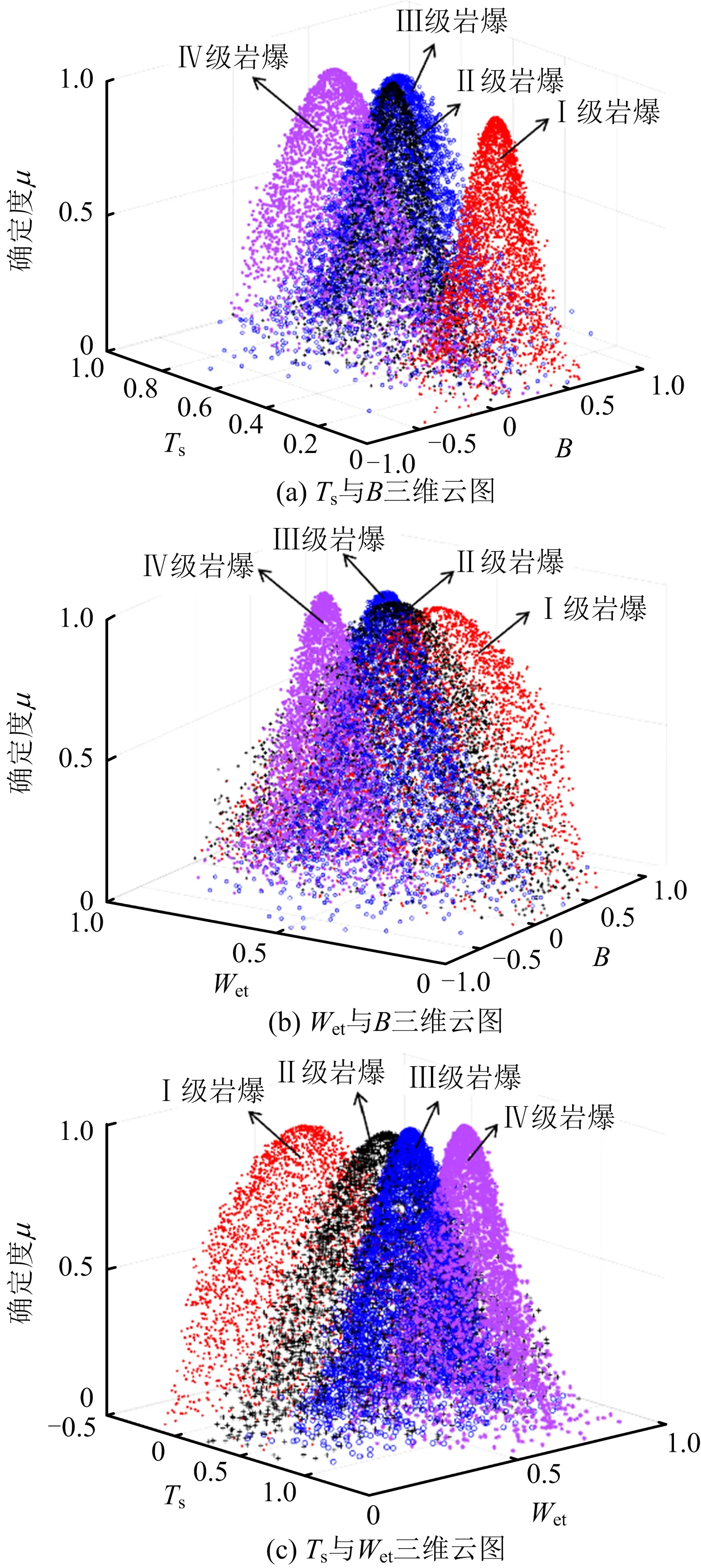
圖6 巖爆實例數據聚類云模型Fig.6 Clustering cloud model of rock burst case data

3.3 求取最優權重

將各數字特征代入式(7)構建適應度函數反求權重，在遺傳算法中，適應度函數的每次使用將重新計算數字特征，確保結果真實性。

常規遺傳算法迭代曲線保留原始樣本最優解，尋求全局最優解，迭代曲線呈現單調上升趨勢。本文由式(7)使用動態適應度函數，同一最優解會出現不同結果，滿足巖爆評價實際情況。為降低時間成本，減少迭代次數，最快獲取較為穩定全局最優解。本文增加種群數量，設置初始化種群數量N=1 000，迭代次數f=100，采用錦標賽選擇和精英保留方法，增加圖3中4個權重約束條件進行約束，運行Matlab最終獲得迭代曲線如圖7所示。

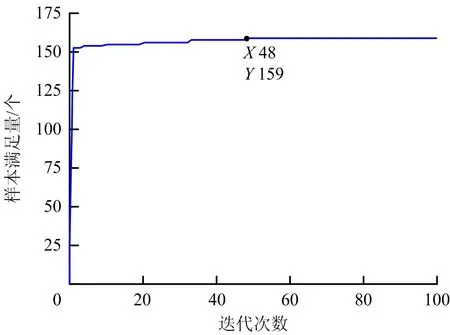
圖7 迭代曲線Fig.7 Iteration curve

由圖7得迭代48 次后滿足條件樣本數量保持穩定，此時各指標最優權重為ωTs=0.632 1、ωWet=0.257 7和ωB=0.110 2，最優權重與假設權重比例相符，滿足樣本實例。

3.4 實例驗證與對比

將所求結果通過前文表1中未參與反求權重的29組實例樣本進行評價。由于巖爆事故本身具有較強隨機性，應將評價結果的合理波動考慮進來，增大預測范圍，分析評價結果更多的可能性。本文對樣本數據進行客觀評價，采取保守預測方法，將確定度差值不足0.1的巖爆等級進行傾向性預測，其預測結果進行跨區間表示，例如：Ⅱ～Ⅲ級巖爆，此方法滿足實際巖爆預測要求，使預測更加嚴謹，并與其他云模型評價方法進行結果對比，進一步驗證本文方法的可靠性與有效性，具體情況見表3。

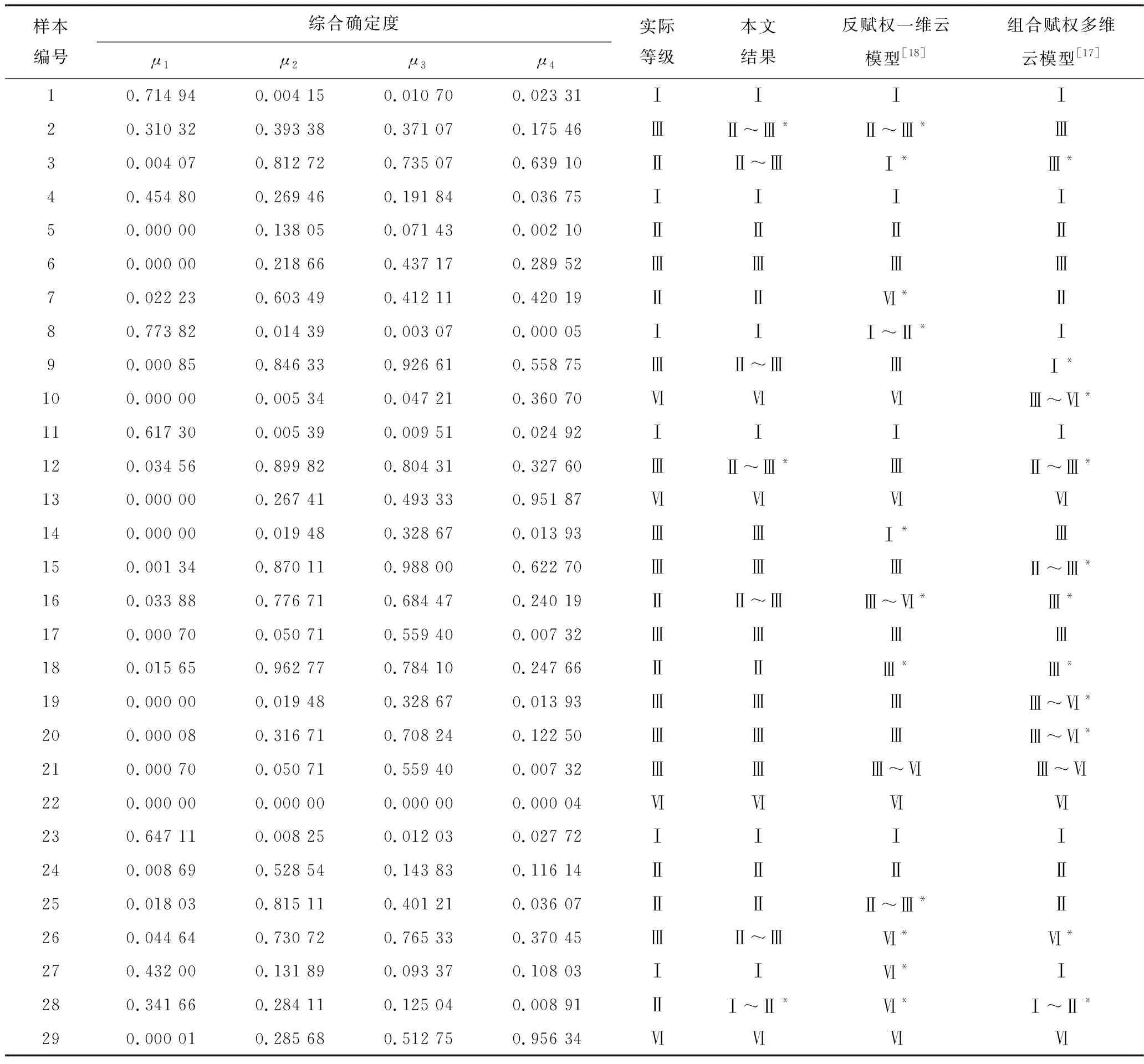
表3 巖爆傾向性評價結果Table 3 Evaluation index judgment interval

結果顯示，預測結果與實際基本相符，與其他模型的預測結果基本吻合。本文與反賦權一維云模型權重確定方法相同。由表3得，反賦權一維云模型傾向性預測準確率為72%。組合賦權多維云模型預測結果準確率為86%，比一維正向云發生器的準確率更高。在逆向云發生器中，MBCT-SR算法與優化算法結合評價精準預測準確率可達89%，傾向性預測準確率可達100%。預測結果對比表明，本文評價模型更加合理且有效，算法充分考慮實際巖爆的隨機性與模糊性，更貼合實際情況。

4 結論

1)結合當前機器學習的熱門方向，依據國內外192 組巖爆實例數據，選取應力比Ts=σθ/σt、巖石脆性指數B=σc/σt以及彈性應變儲能指數Wet作為評價指標，將逆向云發生器與優化算法相結合建立綜合評價模型。本模型引進MBCT-SR算法，規避常規正向云發生器主觀性過強、絕對性較大的缺點，建立更加客觀的多維巖爆預測云模型。

2)指標權重優化結果來自于真實數據與多維云模型。本文依據圖5、6中的數據可視化分析，對權重分布規律進行了滿足ωTs>ωWet>ωB的初步假設，并由最終計算結果求得最優權重為ωTs=0.632 1、ωWet=0.257 7和ωB=0.110 2，對假設進行了科學驗證。使得本指標權重確定方法更加準確嚴謹，最終結果與主觀認知相符。

3)相比其他預測模型可得，本模型最大化降低主觀因素干擾，在選取應力比Ts=σθ/σt、巖石脆性指數B=σc/σt以及彈性應變儲能指數Wet作為評價指標進行預測時，精準預測率達89%，傾向性預測結果準確率可達到100%，其評價結果更加準確、真實。