基于時間序列的網絡失效模型*

嚴玉為 蔣沅 楊松青 余榮斌 洪成

(南昌航空大學信息工程學院,南昌 330063)

隨著網絡科學的發展,靜態網絡已不能清晰刻畫網絡的動態過程.在現實網絡中,個體之間的交互隨時間而快速演化.這種網絡模式將時間與交互過程緊密聯系,能夠清晰刻畫節點的動態過程.因此,如何更好地基于時間序列刻畫網絡行為變化是現有級聯失效研究的重要問題.為了更好地研究該問題,本文提出一種基于時間序列的失效模型.通過隨機攻擊某時刻的節點,分析了時間、激活比例、連邊數、連接概率4 個參數對失效的影響并發現網絡相變現象.同時為驗證該模型的有效性與科學性,采用真實網絡進行研究.實驗表明,該模型兼顧時序以及傳播動力學,具有較好的可行性,為解釋現實動態網絡的級聯傳播提供了參考.

1 引言

隨著網絡科學的進步,網絡已成為分析人類活動與自然現象的有力工具[1?3].隨機網絡模型、小世界網絡模型和以偏好連接的無標度網絡模型都是靜態網絡模型.這些靜態網絡模型適合捕捉網絡中的基本特征,但前提網絡節點之間的連接是長期存在的[4].然而,在現實生活中,個體之間的連接快速演變,例如交通網絡、社交網絡、通信網絡.有必要利用一種有效模型來描述這些動態過程.Perra等[5]首次通過定義活動勢構建活動驅動模型.Liao等[6]基于動態網絡提出節點重要度排序方法.Wang等[7]發現動態網絡在整個網絡過程中所需的能量以及軌跡數量少.目前時序網絡是新興方向,但是研究意義重大,與靜態網絡相比,時序網絡從時間角度考慮節點間的交互,更加精準反映交互過程.因此基于時序網絡的研究已然成為復雜網絡科學的重要研究部分.而網絡健壯性[8?15]也是網絡安全的核心課題之一.級聯故障是現實生活中的常見現象,例如電網崩潰、交通網絡的中斷以及疾病傳播.級聯失效的原因是由于網絡中的故障節點通過滲流作用將失效傳遞到周圍節點從而造成大規模破壞.因此,研究級聯失效能更好理解網絡失效,進而更好地控制級聯失效.

在過去的一段時間,研究者們提出多種級聯失效模型.Motter 等[16]提出線性容量模型(ML 模型),通過模擬連鎖故障對網絡連通性進行評估.實驗結果表明,通過移除較高負載的節點可以造成網絡全局級聯失效.Dou 等[17]針對ML 模型提出一種更為靈活的非線性負載容量模型,進而研究網絡成本與魯棒性之間的關系.實驗表明此模型更加符合現實生活中負載與容量之間的關系.Wang[18]將邊的初始負載定義為節點度的函數,當一條邊的負載超過其自身容量時,邊不會從網絡中移除,而是將自身額外的負載向周圍邊進行傳遞.Li 等[19]將節點或邊的負載定義為節點或邊的最短路徑數量.Wang 等[20]構建一種負載局部重分配的級聯失效模型,并考察無標度網絡的級聯失效.Liu 等[21]提出一種基于多變負載的負載分配策略.通過將節點剩余容量充分利用從而減少網絡級聯失效.唐亮等[22]構建一種故障概率傳播的級聯失效模型,節點故障概率隨故障次數的增加而減少,網絡失效規模減少.Duan 等[23]提出全局分配策略的級聯失效模型.Hao 等[24]提出過載級聯失效模型,并指出網絡節點超出一定容量后并不會失效而是處于過載狀態.

綜上所述,現有級聯失效的研究停留在靜態網絡,而在現實生活中,事件的發生與時間緊密聯系,無論是社交網絡還是交通網絡,這些網絡中節點的接觸都是不斷變化.基于此,本文構建具有時間戳的網絡結構,并以此探討時間參數T、激活比例pactive、連接邊數M、連接概率pcon對網絡的影響,此模型更加符合現實網絡中失效情況,對進一步研究級聯失效具有很強的實用性和現實意義.

2 時序網絡的失效模型

2.1 時序網絡建模

探討時序網絡下級聯失效的前提是對時序網絡進行建模.我們僅考慮網絡中邊的增加與移除,并不考慮節點的出現與消失,也就是說在時序網絡中節點數目不變,連邊隨時間的推移而動態變化.將其表示為G=(vi,vj,t),其中vi和vj分別表示網絡源節點與目標節點,t表示兩個節點之間的接觸時刻.將網絡各個接觸時刻當成一個快照,即快照反映某一時刻發生的所有事件.在此基礎上,通過聚合所有快照進而得到時間聚合圖.其時序網絡快照以及時間聚合圖如圖1 所示.從圖1 可以看出,節點在不同時刻產生的交互次數以及交互對象不同.在時刻T=1 時(見圖1(a)),節點(vA,vB),(vA,vD),(vB,vD),(vD,vC)之間產生連邊.而在時刻T=2 時,節點vA不在與節點vB,vD產生交互,而當時刻T=3 時,節點(vB,vD)之間不在交互,取而代之的則是(vB,vC)之間的交互.以此類推直到時間結束.

圖1 時序網絡圖 (a)T=1;(b) T=2;(c) T=3;(d) T=4;(e) T=5;(f) T=6;(g) T=AllFig.1.Sequential network:(a) T=1;(b) T=2;(c) T=3;(d) T=4;(e) T=5;(f) T=6;(g) T=All.

在時序網絡初始階段中,首先選取部分節點作為初始傳播節點.在時刻1 中(見圖2(a)),每個活躍節點以一定概率隨機向M個節點進行連接.隨后從時刻1 中激活的節點再次選取一定比例的節點作為第2 時刻的初始活躍節點(見圖2(b)).以此進行迭代,直到網絡達到時間最大值或網絡中沒有后繼節點進行傳播,其時序傳播示意如圖2 所示.

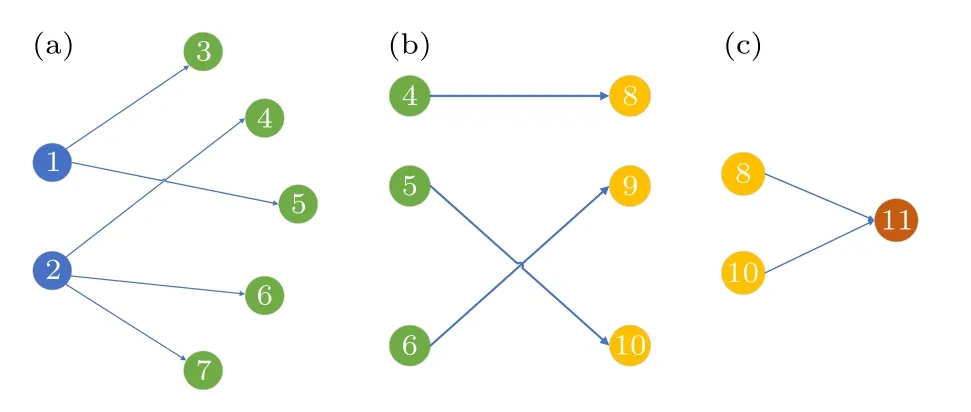
圖2 時序網絡傳播示意圖 (數字表示節點編號) (a) T=1;(b) T=2;(c) T=3Fig.2.Propagation of sequential network (number indicates the node number):(a) T=1;(b) T=2;(c) T=3.

2.2 時序網絡級聯失效

級聯失效是指失效節點引發其他節點失效的一種級聯現象,常見于電力網絡、交通網絡等.為此在本文時序網絡中,通過隨機攻擊某時刻的節點,來觀察時序網絡的失效情況.同時,本文分別給出靜態圖和時序圖的級聯失效,以此顯示靜態圖與時序圖級聯失效差異,從而更好地說明研究時序下級聯失效的必要性.圖3(a)表示靜態網絡,在靜態網絡中,當某節點失效時,失效節點會將自身周圍邊進行無差別斷開.例如當節點vc遭受損壞時,節點vc會將自身邊進行無差別斷開,其網絡拓撲如圖3(b)所示.而在時序圖中網絡被賦予了時間概念,不僅要考慮節點失效,而且還要考慮節點的失效時刻.例如在圖3(c)中節點vA經歷的時刻T=2,4,6 如果節點vA在時刻T=6 失效,那么只會影響節點vB,不影響節點vC,而當節點vA在時刻T=2 失效,其節點vA在T≥2 時都會傳輸錯誤信息進而影響對應時刻的節點.在靜態圖中,規定節點失效條件為受到攻擊或者脫離巨連通網絡,如圖3(b)所示,當節點vC受到攻擊時,網絡破碎成3 個簇結構(A,B),(D,E),(F,G),通過選擇節點數最多的簇作為巨連通網絡(如果簇大小相同則隨機選擇),其他節點失效.而在時序圖中,節點并不會移除與增加,當一個節點在某一時刻受攻擊時,該節點只會對以后時刻產生影響而不會影響之前時刻.同時,注意到在時序網絡中一個節點vI在某一時刻會同時接收一定數量的錯誤信息NTfail與正確信息NTcorrect,如圖3(c)所示,假設節點vC在時刻3 受到攻擊,則節點vG在時刻5 分別收到節點vF,vC,vE傳來的信息.其中節點vE受到節點vC的影響導致節點vE在時刻5 傳輸錯誤信息,而節點vF則不受節點vC影響,其傳輸正確信息.因此節點vG在時刻5 接受了1 個正確信息,2 個錯誤信息.其在時刻5 失效概率為pfail=0.64.因此,利用一個概率函數p進行模擬節點容錯能力:

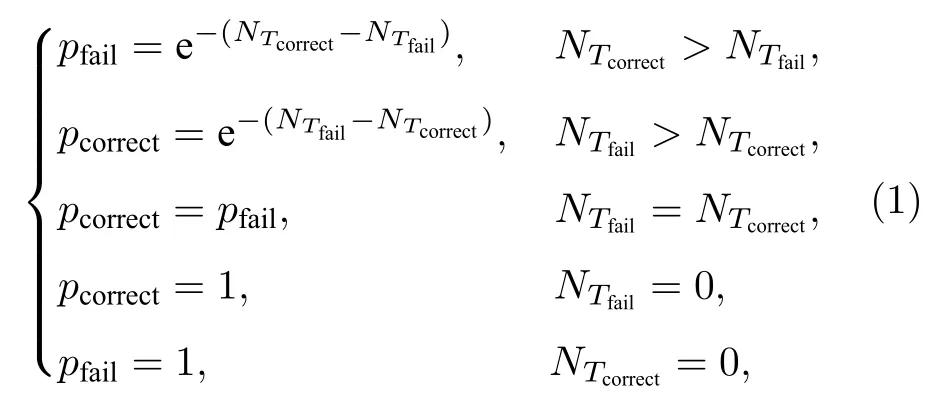
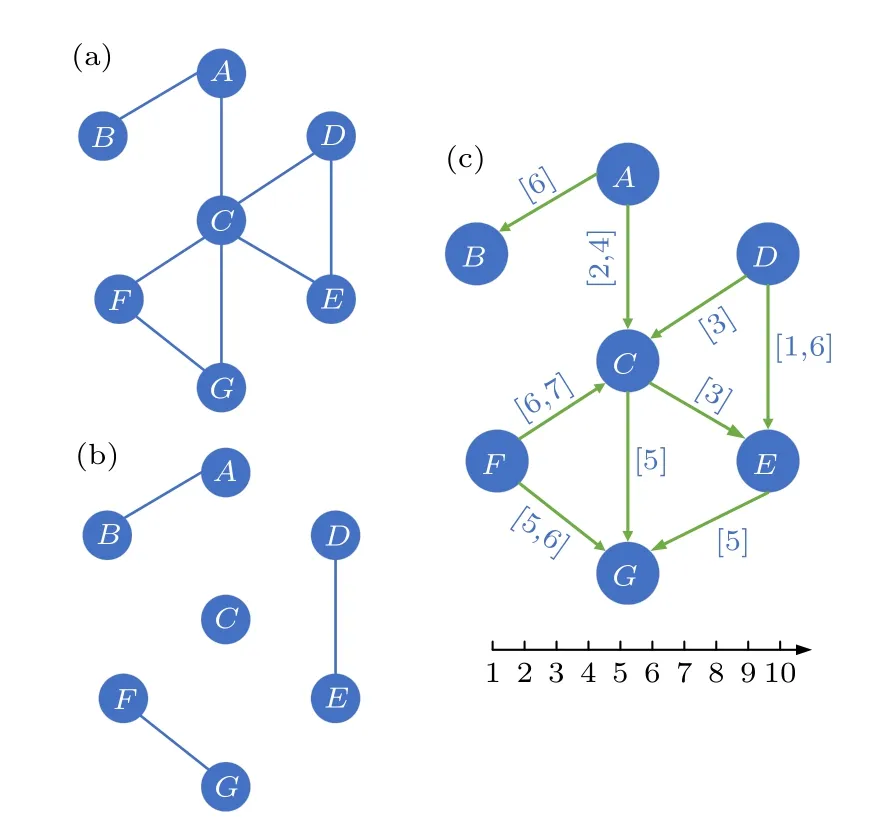
圖3 靜態圖與時序網絡圖 (a) 靜態圖;(b) 靜態網絡失效圖;(c) 時序圖Fig.3.Static diagram and sequential network diagram:(a) Static diagram;(b) static network failure diagram;(c) sequential network.

其中,NTcorrect表示節點在T時刻接受的正確信息數量;NTfail表示節點在T時刻接受的錯誤信息數量.

2.3 時序網絡抗級聯失效魯棒性測試

本文將網絡魯棒性度量指標設為節點在受到攻擊以后執行的交互次數N′與時間聚合窗口內節點進行的交互總數N之比.即G=N′/N.其中G值越大說明網絡損壞程度越大,說明此時網絡的魯棒性越差.

3 仿真結果及分析

首先構建時序網絡:在初始時刻,選取一定比例的初始節點,以連接概率隨機激活M個節點,隨后從上一階段激活的節點中選取一定比例的節點作為傳播節點進行下一時刻的傳遞,直到時間結束或者沒有后繼節點.本文設網絡具有200 節點,通過對網絡進行隨機攻擊來觀察網絡的失效程度,為了避免實驗的隨機性,所有結果均運行500 次并取平均值.

3.1 激活參數pactive 對網絡的影響

為了探索激活參數對時序網絡的影響,令連邊概率pcon=0.3,時間T=5,連邊數M=5,攻擊比例p從0 開始,以此來觀察網絡魯棒性的變化.取pactive=0.1,0.2,0.3,0.5,0.6,1.0 時的仿真結果如圖4 所示.

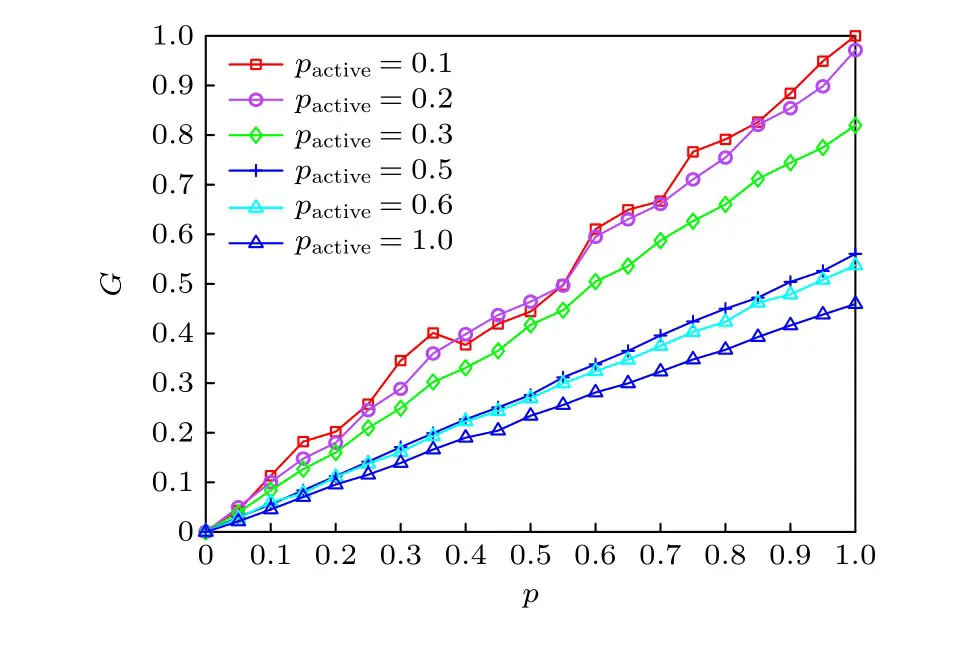
圖4 不同激活參數的網絡魯棒性Fig.4.Robustness of networks under different activation parameters.

從圖4 可以看出,網絡失效程度隨激活參數的增大而減小.在時序網絡中,激活參數影響每次迭代時間步內節點活躍度.節點活躍度高的節點會向下激活節點活躍度低的節點.當網絡中節點活躍度高的數目較高時,信息衰減率就更低,節點交互數目變大.從圖4 中得知,雖然網絡魯棒性隨著活躍參數的增大而增大,但是抗毀性的變化卻不是線性的.其中pactive從0.2 到0.5 變化時,網絡抗毀行性提升最多,此后抗毀性提升在逐漸變小.在實際生活中,信息傳播是不斷衰減的,通過信息論可知,現實中信息衰減率較高.因此,信息衰減的減少能夠帶來網絡抗毀性的提高.同時為了更加直觀地展示激活參數在網絡中的作用,給出不同激活參數下的網絡結構特征(見表1),其中n為節點總數,m為網絡連邊總數,〈kin/out〉 分別為平均入度和平均出度,其網絡拓撲圖如圖5 所示.

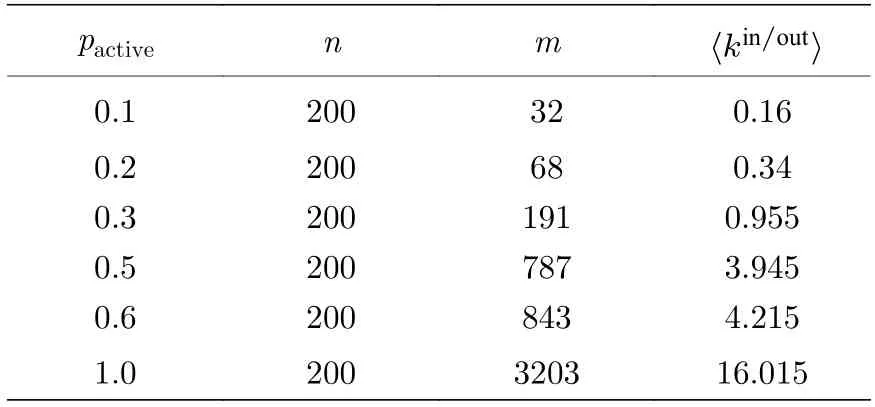
表1 激活參數下的網絡特征Table 1.Statistical characteristics of the networks under activation parameters.

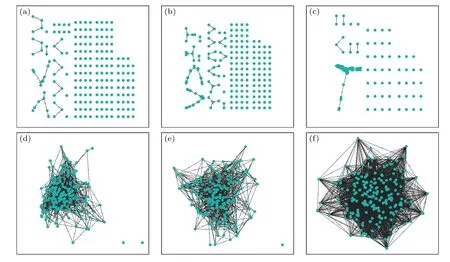
圖5 不同激活參數下的網絡生成圖 (a) pactive=0.1;(b) pactive=0.2;(c) pactive=0.3;(d) pactive=0.5;(e) pactive=0.6;(f) pactive=1.0Fig.5.Network diagram with different activation parameters:(a) pactive=0.1;(b) pactive=0.2;(c) pactive=0.3;(d) pactive=0.5;(e) pactive=0.6;(f) pactive=1.0.

3.2 連邊數M 和連接概率 pcon 對網絡的影響

分別設置pactive=0.3,pcon=0.3,T=5,M=1,2,5,8,10 以及pactive=0.3,時間T=5,連邊數M=5,連接概率pcon=0.1,0.2,0.5,0.6,1.0.在隨機攻擊策略下,分析連邊數以及連接概率對網絡魯棒性的影響.其仿真結果如圖6 所示.

從圖6(a)可以看出,網絡魯棒性隨著連接數目以及連接概率的增加而提升.從圖中可以清晰看出:連邊條數的增加對于網絡魯棒性的提升是有限的.網絡連邊表示的是節點自身的影響力.當一個節點連接數越大,那么該節點就會與更多節點產生接觸,也就表示一個節點在某一個時刻可以同時接受多個節點的連邊,節點受到錯誤信息的影響變小.這與現實生活中謊言傳播極為相似,當某個人同時接收相同數量的錯誤信息和正確信息后,那么這個人就會面臨二選一情況,而當另外一個人提供了正確信息后,那么就大大增加選對概率.而連接概率表示的是節點連接效率,即產生有效接觸數.如圖6(b)所示,隨著連接概率的增加,網絡魯棒性有限提高.因此,連接數以及連接概率對網絡魯棒性的影響相輔相成,兩者之間存在著關聯.其連邊參數下的網絡生成圖如圖7 所示.表2 表示不同連邊條數以及連接概率下的網絡結構特征,其中n為節點總數,m為連邊總數,〈kin/out〉 分別為平均入度和平均出度.

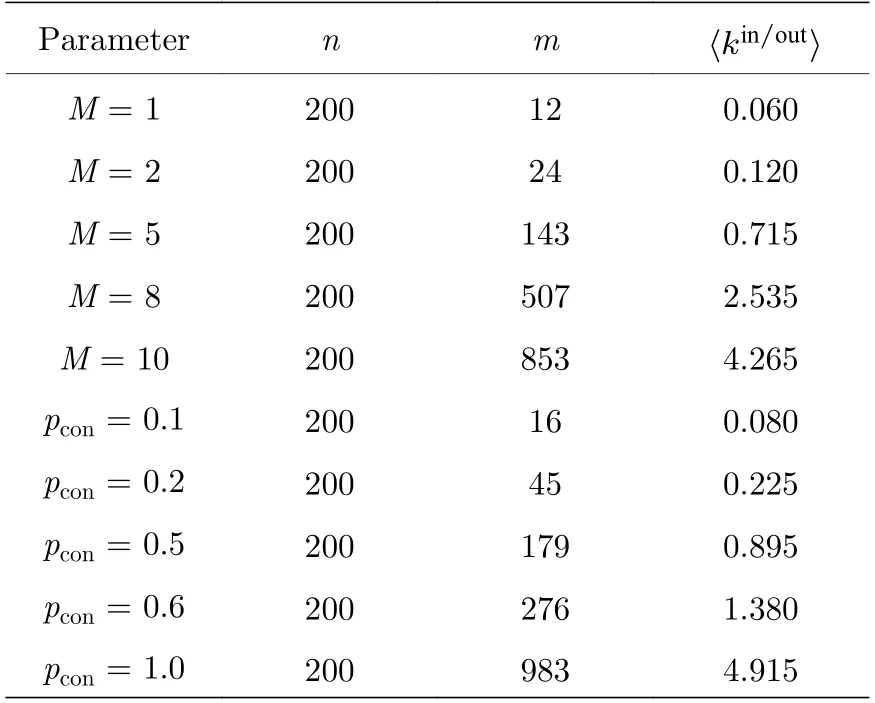
表2 不同連接數以及連接概率下的網絡特征Table 2.Statistical characteristics of the networks under different connection numbers and connection probabilities.

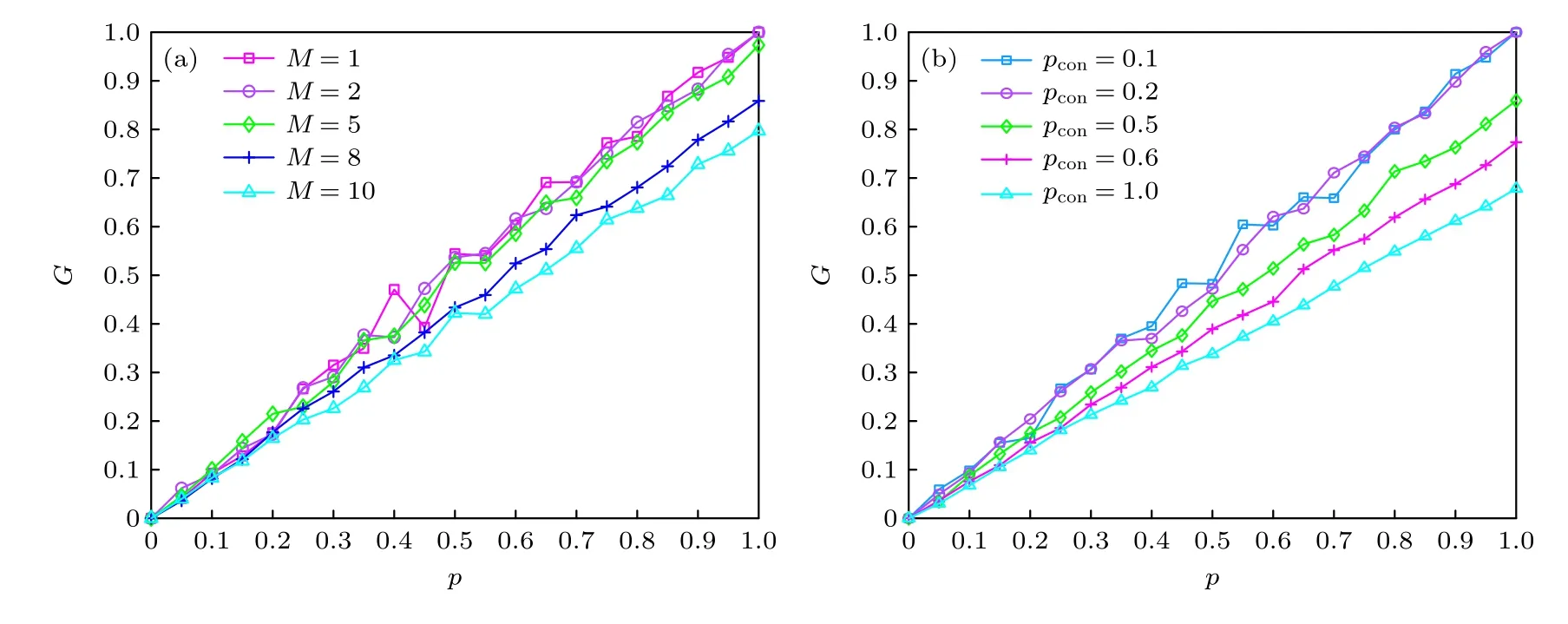
圖6 不同邊數以及連接概率下的網絡魯棒性 (a)不同連邊數;(b)不同連接概率Fig.6.Network robustness under different connection numbers and connection probabilities:(a) Different edge numbers;(b) different connection probabilities.

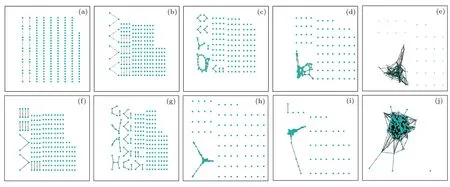
圖7 不同連接數以及連接概率下的網絡生成圖 (a) M=1;(b) M=2;(c) M=5;(d) M=8;(e) M=10;(f) pcon=0.1;(g) pcon=0.2;(h) pcon=0.5;(i) pcon=0.6;(j) pcon=1Fig.7.Network diagram with different connection numbers and connection Probability:(a)M=1;(b)M=2;(c) M=5;(d) M=8;(e) M=10;(f) pcon=0.1;(g) pcon=0.2;(h) pcon=0.5;(i) pcon=0.6;(j) pcon=1.

3.3 連邊數M 與激活參數pactive 對網絡的影響

分別設置pcon=0.3,T=5,M=2,3,4,5,6,并讓pactive從0.05 開始變化以此來觀察網絡魯棒性.其仿真結果如圖8 所示.

從圖8 可以看出,網絡魯棒性在連邊數以及激活參數的影響下表現并不均衡.當pactive=0.45時,網絡魯棒性發生了相變現象,并且隨著連邊數M的不同,網絡魯棒性表現也不同.其中網絡魯棒性在M=2,3,4,5,6 時分別提高了11.36%,17.8%,22.8%,24.9%,30.4%.同時從圖8 可以看出當pactive<0.45,網絡魯棒性在區間M=4—5提升最多.而當pactive>0.45 時,網絡魯棒性在區間M=2—3 提升最多,這一發現為解釋和保護現實網絡提供了重要參考.

圖8 網絡魯棒性Fig.8.Network robustness.

3.4 時間參數T 對網絡的影響

為了探索時間參數T對時序網絡的影響,令pactive=0.3,M=5,pcon=0.3,攻擊比例p從0開始,以此來觀察網絡魯棒性的變化.取T=2,5,10,20,30 時的仿真結果如圖9 所示.

圖9 不同時間下的網絡魯棒性Fig.9.Network robustness under different time.

從圖9 可以看出,網絡魯棒性隨著時間T的延長并沒有明顯變化.在時序網絡中,時間T表示網絡中節點與節點可接觸的最大時間.隨著時間T的延長,節點與節點可接觸的時刻變多,網絡也愈加復雜.當網絡中一個節點因失效而發送錯誤信息時,由于錯誤信息會受到正確信息的限制,時間越大,這種限制越強.這與現實生活是極為類似的.然而圖9 結果卻不相同.通過分析發現是由于激活參數以及連接概率相對較小造成的.表3 表示不同時間下的網絡結構特征.同時,為了更加直觀地觀察,其網絡結構圖如圖10 所示.

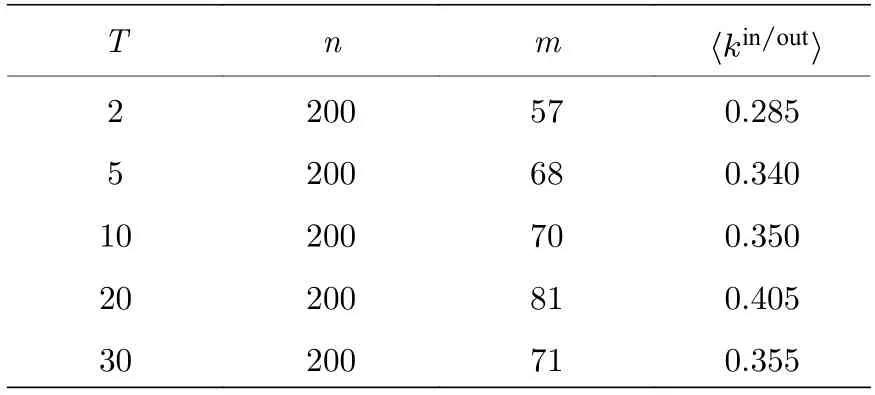
表3 不同時間下的網絡特征Table 3.Statistical characteristics of the networks under different time.

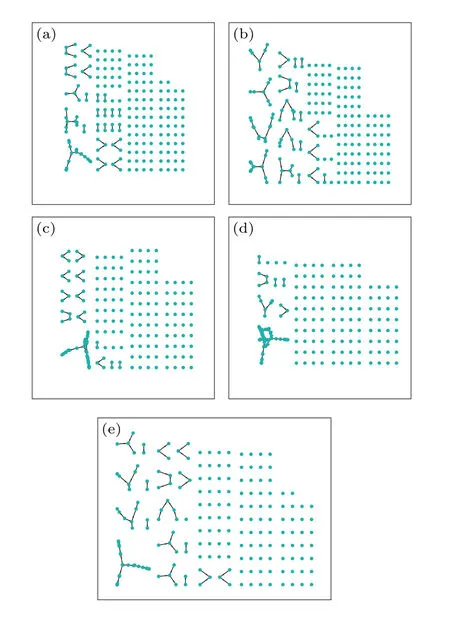
圖10 不同時間下的網絡生成圖 (a) T=2;(b) T=5;(c) T=10;(d) T=20;(e) T=30Fig.10.Network diagram under different times:(a) T=2;(b) T=5;(c) T=10;(d) T=20;(e) T=30.

從圖10 可以看出,網絡中節點之間并沒有生成連通圖,而是幾個簇.因此將設參數pactive=0.6,連邊數M=5,連接概率pcon=0.6.其網絡失效如圖11 所示.

由圖11 可以看到,網絡魯棒性隨著時間參數的增大而增強.此時再觀察網絡結構圖,其如圖12所示.同時,網絡特征如表4 所示.

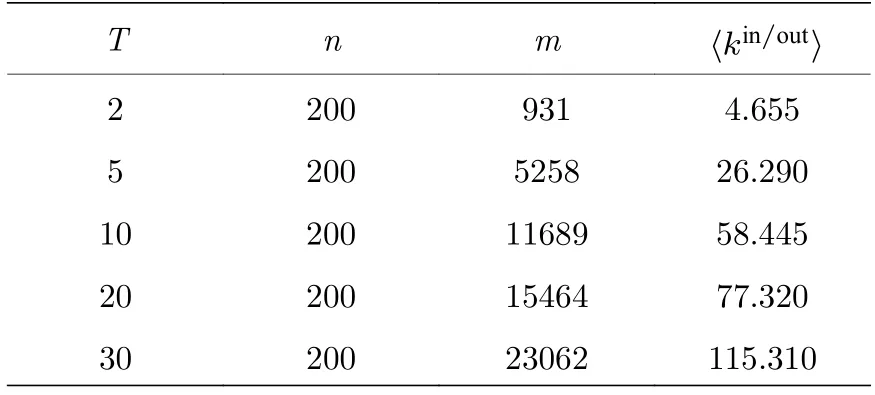
表4 不同時間下的網絡特征Table 4.Statistical characteristics of the networks under different times.

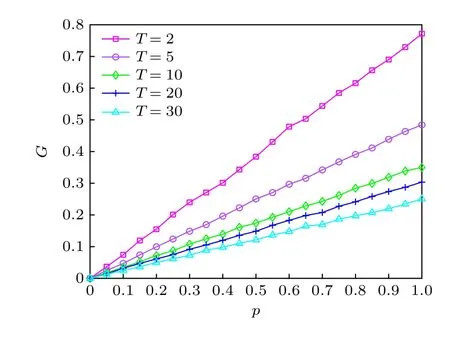
圖11 不同時間參數的網絡魯棒性Fig.11.Network robustness under different time.

通過圖12 可以看出,在激活參數以及連邊概率參數增大后,網絡在時刻T=5 時變為連通圖.隨著T的增大,網絡愈加復雜,網絡抗毀性得到進一步增強.同時,為了更好地與實際相結合,以美國小型社交網絡為例分別仿真了靜態網絡的級聯失效以及時間序列的級聯失效.該數據集描述的是35 個人在間隔1 h 的接觸情況,其網絡失效圖以及接觸情況如圖13 和表5 所示,美國小型社交網絡的結構特征n=35,m=118,〈kin/out〉=3.3714.

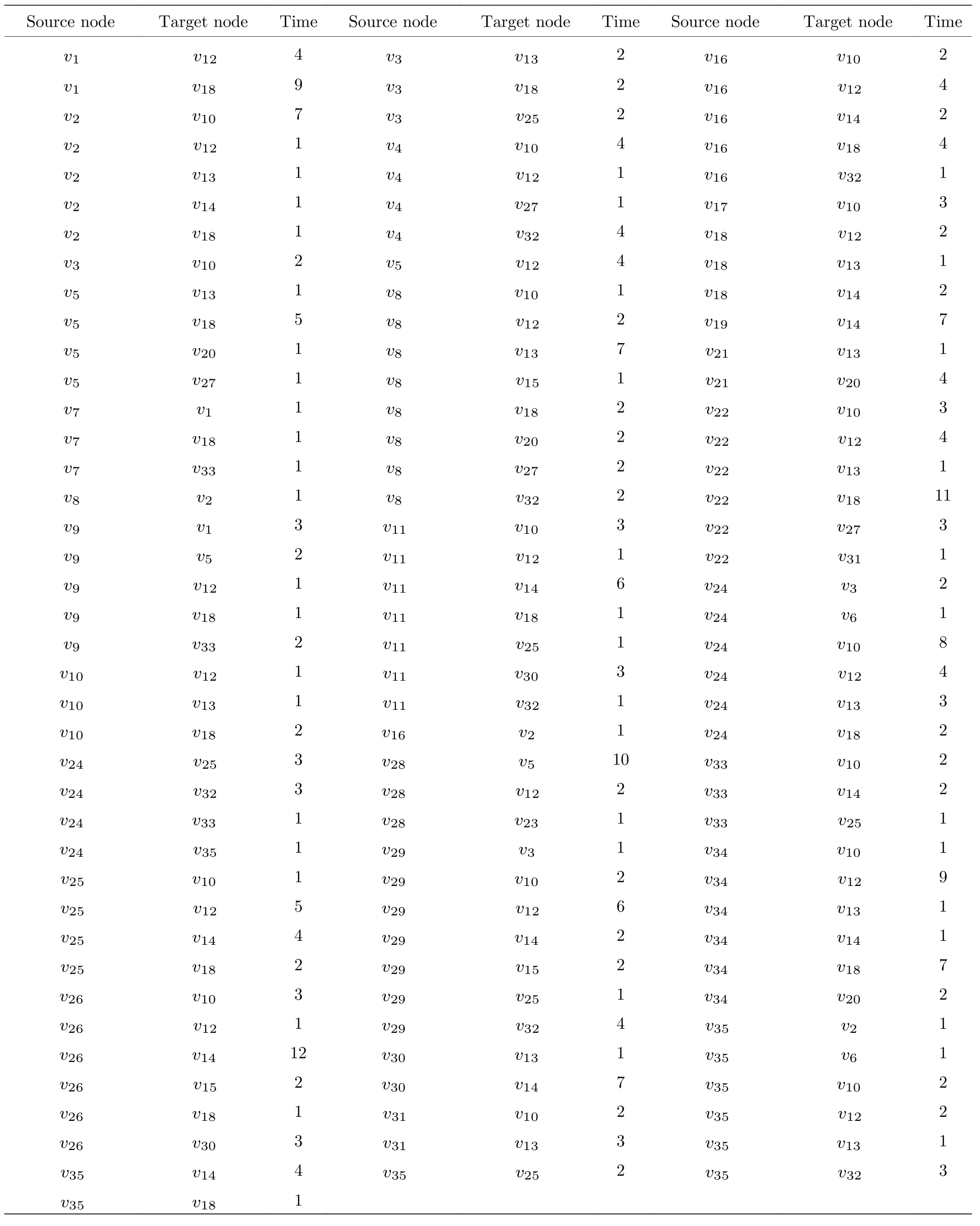
表5 美國小型社交網絡的接觸時刻Table 5.Contact time of small social networks in the United States.

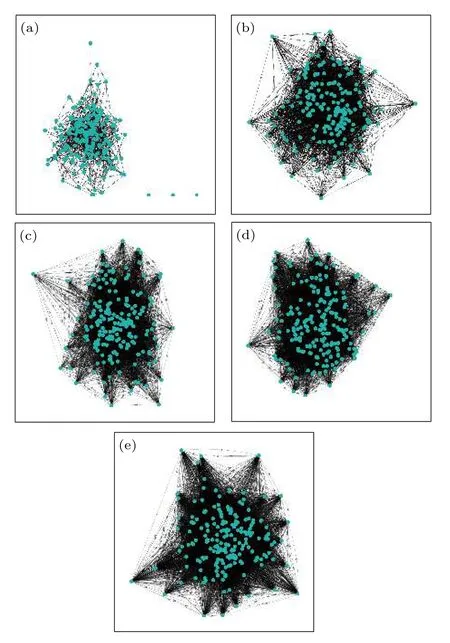
圖12 不同時間下的網絡圖 (a) T=2;(b) T=5;(c) T=10;(d) T=20;(e) T=30Fig.12.Network diagram under different times:(a) T=2;(b) T=5;(c) T=10;(d) T=20;(e) T=30.

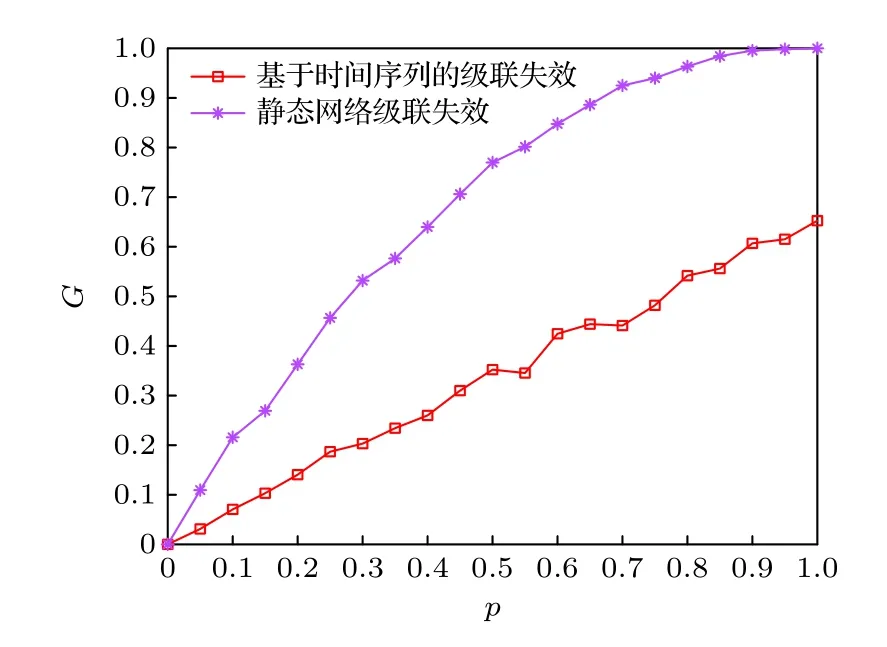
圖13 美國小型社交網絡級聯傳遞規模圖Fig.13.Scale of transmission through small social networks in the United States.

通過本文的級聯傳播理論,其失效規模的傳遞規模如圖13 所示.從圖13 可以看到,即使在初始階段中受影響人群規模達到100%,但是由于人群所處的時刻不一樣,失效信息的傳遞隨著拓撲結構的變化而變化.其傳遞只會影響發生時刻之后的時間,因此,網絡抗毀性提高.與之對比,靜態網絡在遭受攻擊以后會出現大規模節點永久性失效,如圖3(b)所示,當節點vc失效時,其節點以及自身連邊會無差別永久性失效,同時造成其他節點脫離巨連通網絡失效,以此網絡出現大規模失效.而在本文所提模型中,傳播過程中遵循一定的方向性、時間性.因此,面對攻擊,靜態網絡相對于時間序列的網絡是極其脆弱的,這一方面從圖13 可以得出.

4 結論

隨著網絡科學的發展,靜態網絡已不能清晰刻畫網絡的動態過程.為了突破現有研究的局限性,提出了時序網絡下的級聯失效,此模型將網絡交互賦予了時間概念,相對于傳統的級聯失效模型不僅考慮網絡的拓撲結構還考慮節點接觸時刻.通過對節點的某時刻進行隨機攻擊,有效地分析了動態網絡下級聯反應行為.同時,發現激活參數、連邊數、時間、連邊概率對時序網絡的抗毀性起著重要作用,更為重要的是發現了時序網絡的相變現象.

最后,為了驗證該模型的有效性與可行性,引入真實網絡進行分析.實驗顯示,本文提出的模型能更好地從時間角度進行描述與分析級聯失效,為研究級聯失效提供了重要參考.未來將進一步考慮將所提模型應用到實際中,例如電網、交通網等.