主動隨機送風條件下大口徑離軸三反光學系統的計算機輔助裝調

羅 敬，王金鑫，2，鞠國浩，尤晨旭，劉奕辰，徐天曉，2，李成浩，姜成強，馬銘澤，2，何 煦，張曉輝，董吉洪，徐抒巖*

（1.中國科學院 長春光學精密機械與物理研究所，吉林 長春130033；2.中國科學院大學，北京100049）

1 引 言

三反消像散光學系統具備寬光譜、大視場、高成像分辨率、易控制雜散光等特性，在對地遙感、天文觀測中得到了廣泛的應用［1］。JWST［2］、CSST［3-4］、Euclid［5］、HabEx［6］和WFIRST-A［7］等均屬于三反消像散光學系統。離軸三反光學系統因孔徑離軸或視場離軸實現了無中心遮攔，這有利于提高系統的光通量和點擴散函數（Point Spread Function，PSF）質量。然而，離軸系統的非旋轉對稱性卻增加了裝調難度，傳統的定心裝調方法不再適用，因此，光學裝調成為研制離軸三反光學系統的主要難點之一［8-11］。

隨著科學技術的發展，成像觀測精度的要求越來越高，進而迫使高分辨率光學系統朝大口徑、長焦距方向發展。哈勃望遠鏡主鏡口徑2.4 m，系統焦距達到57.6 m［12］，其繼任者JWST的口徑更是達到6.5 m，系統焦距為131.4 m［2］。不斷增大的口徑和焦距進一步增加了光學系統的裝調難度。一方面，隨著口徑的增大和像質的提高，光學系統中各個鏡體的裝調公差要求更為嚴格；另一方面，目前大多數計算機輔助裝調方案均將系統波像差作為主要的輸入信息，其檢測精度直接決定了系統裝調的效率和質量［13］。然而，大口徑、長焦距光路中氣流擾動成為決定系統波前檢測精度的關鍵因素，這會對光學裝調造成重要影響。因此，抑制光學檢測中的氣流擾動具有重要意義。

Shi［14］和陳華等［15］理論分析了氣流擾動對折射率空間分布的影響機理，建立了相應的數學模型，并計算了不同狀態下氣流對波前像差的影響。姜自波等［16］結合理論分析和實驗測量，深入研究了氣流擾動對單鏡面形檢測結果的影響。徐抒巖等［17］針對氣流擾動下大口徑光學系統在實驗室環境下裝調困難的難點，提出通過主動送風來抑制氣流擾動對波前檢測的影響，取得了較好的效果。本文在此基礎上，進一步提出結合主動隨機送風和動態干涉儀多次平均累加的裝調方案，降低了對風扇陣列的要求，提高了方案的可靠性和可實施性。通過Fluent軟件仿真和多次實驗迭代，優化了風扇數量、位置、朝向和風速等風場設置，最終較好地抑制了氣流擾動對大口徑、長焦距光學系統波前檢測的影響。最后，在主動隨機送風條件下完成了一個0.5 m口徑、6 m焦距離軸三反光學系統的裝調，取得了良好的收斂效果和系統像質。

2 基本原理

基于靈敏度矩陣的計算機輔助裝調是目前應用最廣泛的裝調方法，其基本原理是：小失調范圍內系統各個視場的Zernike系數變化量與失調量之間近似滿足線性關系［13］。其數學模型可以表示為：

其中：ΔX為系統各個維度的失調量；A為靈敏度矩陣；ΔF為各項波像差的變化量，通常用各個視場波像差的Zernike多項式擬合系數來表示。若靈敏度矩陣A為滿秩矩陣，則式（1）存在唯一解，有：

即通過靈敏度矩陣的逆與各視場Zernike系數變化量的乘積便可得到失調量。然而，在離軸三反消像散光學系統中，次鏡和三鏡各個維度對系統波像差的影響并不是相互獨立的。比如，次鏡沿Y軸的偏心與次鏡和三鏡繞X軸的傾斜均存在補償。這表明靈敏度矩陣A的各個列向量不是線性無關的，不能通過線性組合表示出同等維度空間內的任意列向量ΔF。因此，靈敏度矩陣A不是滿秩，屬于奇異矩陣，不存在嚴格的逆［18］。綜 上，式（1）是 矛 盾 方 程 組，不 存 在 解析解。

在許多實際問題中，線性方程組往往都是不相容的，即方程組沒有嚴格意義的解。在這種情況下，人們追求的目標是得到不相容方程組的最優解，即最小二乘解。對于一個失調的光學系統，輸入更多的像差信息可以更加真實地反映出系統的失調情況，從而更有利于找到方程組的最優解。因此，通常的做法是增加方程的數目，即矩陣A的行數。這導致矩陣A不再是方陣，其行數大于列數。此時，式（1）變為一個超定方程。根據多元函數的極值理論及矩陣運算和求導規則，該超定方程的最小二乘解為［13，18］：

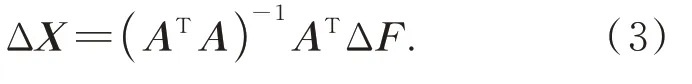
式（3）也被稱為法方程或者正則方程。然而，該正則方程的求解依然存在缺陷，即其條件數通常很大。這是因為離軸三反消像散光學系統中失調維度多，且波像差與失調參數之間的函數關系十分復雜，次鏡和三鏡各個維度失調量之間存在較為嚴重的互相關［13，19］。若系統的靈敏度矩陣A與測量結果ΔF均不存在誤差，通過式（2）可以解算得到正確的失調量。然而，在測量時不可避免地會存在測量誤差，大條件數會導致解算結果極易受到測量誤差的影響而出現大范圍波動，使得解算的失調量失真［20］。

建立線性方程組：

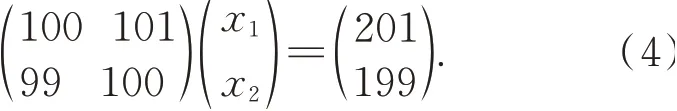
顯然，該方程的精確解為X=(1 1)T。若右側矢量存在微小的擾動，即：

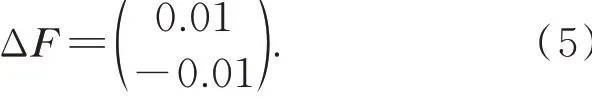
則式（4）變為：

其解變為X=(3.01-0.99)T。盡管右側矢量的擾動量很小，擾動前后方程的解卻差異很大，若將擾動后的解作為最終結果會導致結果嚴重失真。

3 Zernike系數測量誤差對計算機輔助裝調的影響

輸入參數測量誤差會導致大條件數靈敏度矩陣的解出現大偏差。為了抑制大條件數靈敏度矩陣失調量解算結果隨Zernike系數測量誤差波動性大的問題，阻尼最小二乘法被提出［21］。盡管通過添加阻尼因子，可以有效減小靈敏度矩陣的條件數，避免失調量解算結果失真。然而，大的Zernike系數測量誤差還是會降低裝調結果的收斂效率，裝調結果會隨Zernike系數誤差在一定范圍內波動，導致次鏡和三鏡各個維度存在較大的裝調殘差。本文將基于一個0.5 m口徑、6 m焦距的離軸三反光學系統，通過數值仿真來說明Zernike系數測量誤差對計算機輔助裝調的影響。

圖1為離軸三反消像散系統光路，系統包含主鏡、次鏡和三鏡，它們均為二次曲面。該系統焦距為6 m，入瞳直徑為0.5 m，有效視場為1°×1°，各視場設計平均波像差RMS為0.05λ。本文分別計算了無Zernike系數誤差、Zernike系數標準差σ=0.005以及σ=0.05三種情況下，次鏡和三鏡各個維度失調后經計算機輔助裝調的收斂情況，每種情況下進行10組蒙特卡洛仿真計算。需要特別指出的是，三種情況下光學系統的初始失調量是以相同標準差隨機生成的。當無Zernike系數測量誤差時，裝調前后系統各個視場的波像差如圖2所示（彩圖見期刊電子版）。顯然，經計算機輔助裝調后，各個視場的波像差回到了設計水平。次鏡和三鏡各個維度的裝調殘差均為0，如圖3所示。

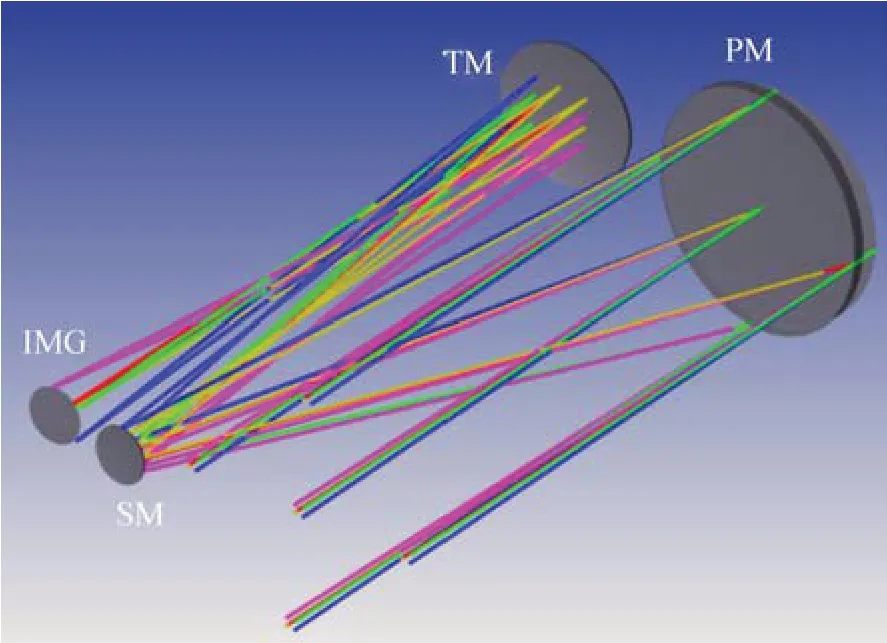
圖1 離軸三反系統光路Fig.1 Optical layout of off-axis three-mirror anastigmat telescope

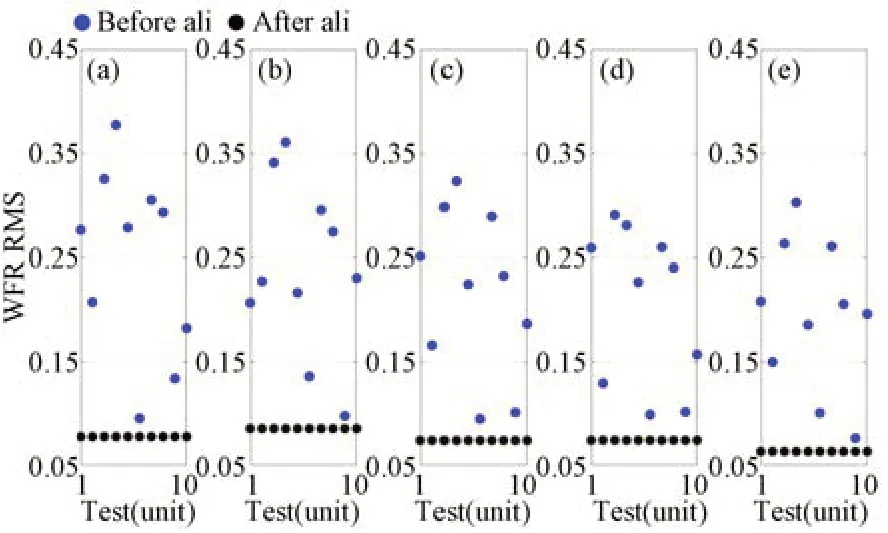
圖2 無Zernike系數測量誤差時裝調前后光學系統各個視場的波像差RMSFig.2 Wavefront errors of optical system at different FOVs without measurement errors of Zernike coefficients

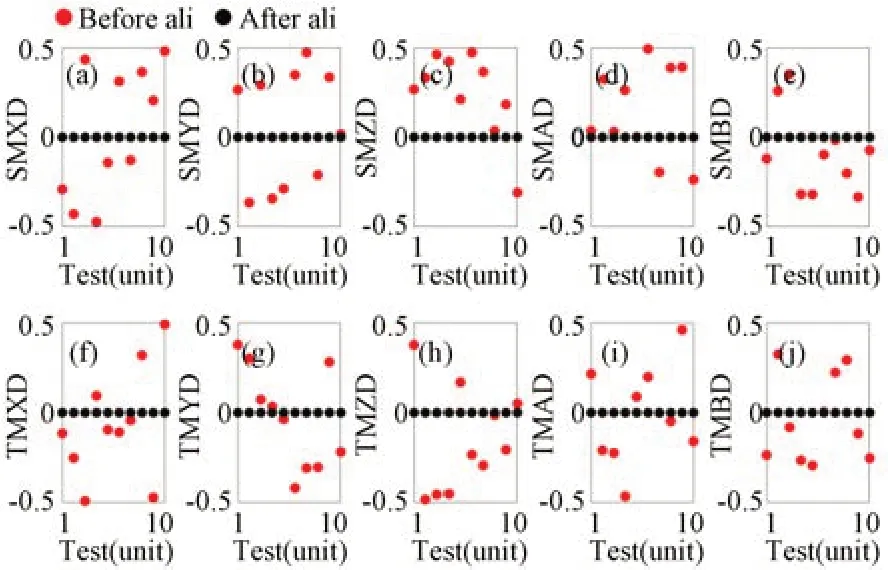
圖3 無Zernike系數測量誤差時裝調前后次鏡和三鏡各個維度的殘余失調量Fig.3 Misalignments of SM and TM without measurement errors of Zernike coefficients

當存在標準差σ=0.005的Zernike系數測量誤差時，系統波像差和各維度失調量裝調結果分別如圖4和圖5所示。可以看出，系統各個視場的波像差基本可以收斂到設計狀態，但是相比較于圖2，存在一定波動。次鏡和三鏡各個維度存在一定的裝調殘差，如圖5所示，尤其是三鏡沿Y軸偏心和繞X軸傾斜。將Zernike系數測量誤差進一步增大，使其標準差σ=0.05，結果分別如圖6和圖7所示。顯然，各個視場的波像差已很難收斂到設計狀態，次鏡和三鏡的裝調殘差也明顯變大。

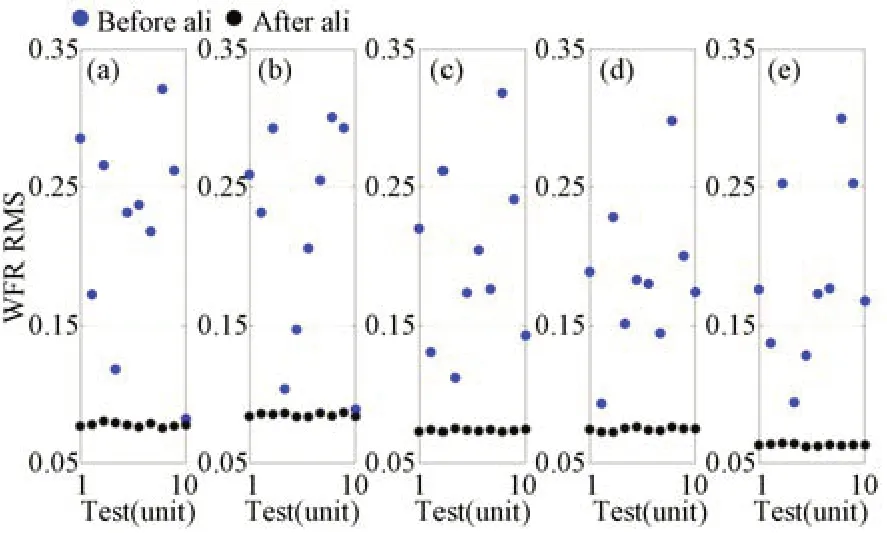
圖4 Zernike系數測量誤差σ=0.005時裝調前后光學系統各個視場的波像差RMSFig.4 Wavefront errors of optical system at different FOVs with measurement errors of Zernike coefficients with standard deviationσ=0.005

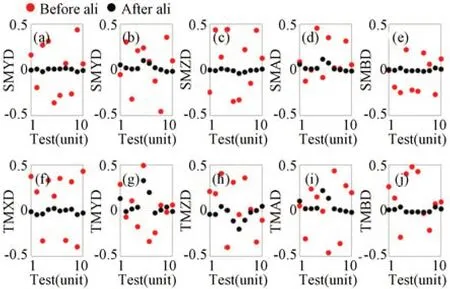
圖5 Zernike系數測量誤差σ=0.005時裝調前后次鏡和三鏡各個維度的殘余失調量Fig.5 Misalignments of SM and TM with measurement errors of Zernike coefficients with standard deviationσ=0.005

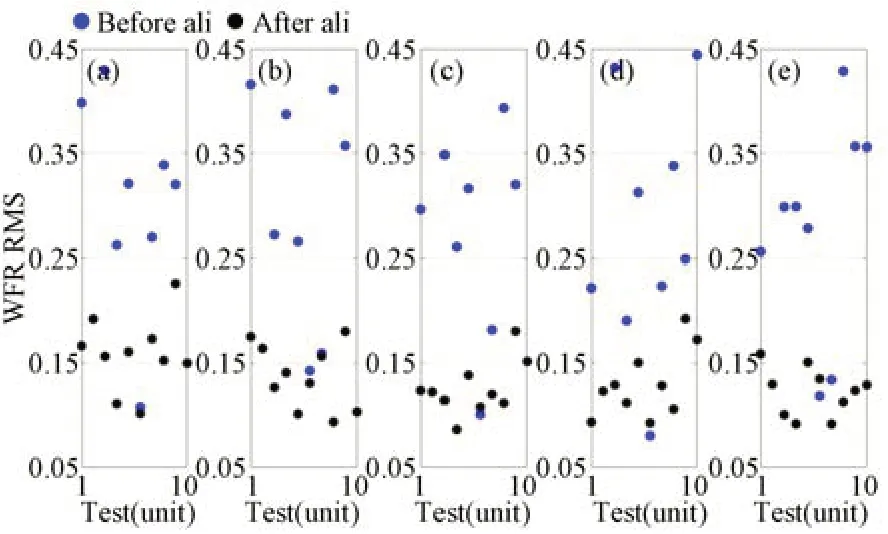
圖6 Zernike系數測量誤差σ=0.05時裝調前后光學系統各個視場的波像差RMSFig.6 Wavefront errors of optical system at different FOVs with measurement errors of Zernike coefficients with standard deviationσ=0.05

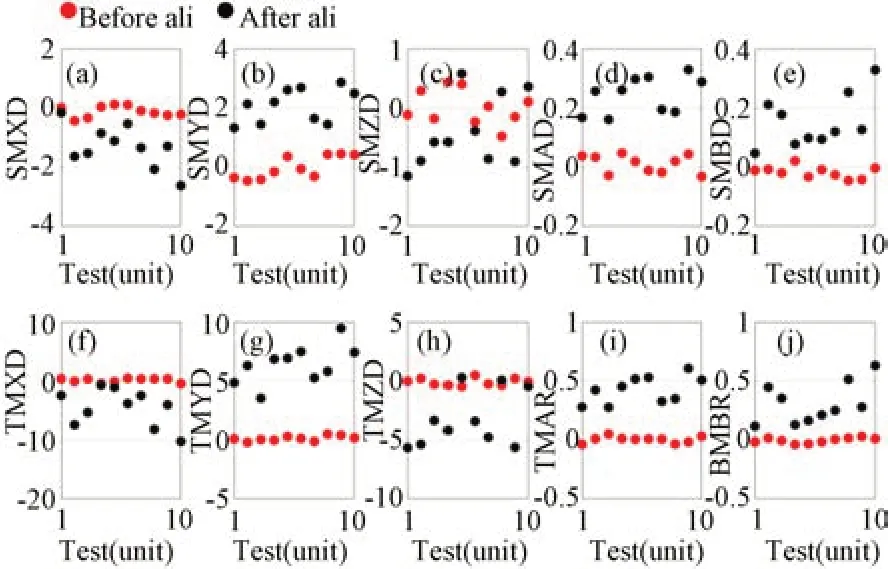
圖7 Zernike系數測量誤差σ=0.05時裝調前后次鏡和三鏡各個維度的殘余失調量Fig.7 Misalignments of the SM and TM with measurement errors of Zernike coefficients with standard deviationσ=0.05

上述仿真結果表明，基于波前檢測的計算機輔助裝調結果會受到Zernike系數測量誤差的顯著影響。Zernike系數測量誤差過大，會導致離軸三反光學系統中次鏡和三鏡各個維度的裝調殘差增大，系統波像差的波動性變大，甚至無法收斂。

增大通光口徑是光學系統提高成像分辨率的主要手段。隨著口徑的增大，氣流擾動成為影響系統波前檢測精度，進而影響系統裝調效率和質量的關鍵因素。目前，不管是實驗室極限溫控，還是使用大型真空罐，均需要付出極大的經濟和時間成本。針對上述問題，本文在基于主動送風的大型光學系統波前檢測氣流擾動抑制方案［17］的基礎上，結合理論仿真和實驗迭代，進一步優化了風場設置，將各個風扇的朝向隨機化，徹底擾亂干涉檢測光路中的折射率場，使它變成隨機分布，并通過動態數字干涉儀的快速多次累加，得到了穩定的干涉檢測結果。

4 主動隨機送風條件下的Zernike系數測量

實驗系統如圖8所示，由一個6 m焦距、0.5 m有效通光口徑的離軸三反消像散光學系統、兩個六足調整臺、自準直平面反射鏡、干涉儀和風扇等組成。結合前期Fluent軟件仿真結果，并經過多次實驗迭代，更改風扇位置，將水平朝向［17］改為置于干涉光路的下方，進而采取由下往上的方式進行主動送風，并優化了風扇到系統光軸的間距。為擾亂整個光路的溫度場和折射率場，需確保風扇陣列充滿整個干涉檢測光路，且所有風扇均搖頭擺動，朝向角度隨機，各個風扇之間的相對位姿也隨機，最終使得干涉檢測光路的氣流隨機分布。

圖8 離軸三反系統自準直干涉檢測光路Fig.8 Optical path for self-collimating interference detection of off-axis three mirror anastigmat telescope

為驗證主動隨機送風條件下大口徑、長焦距光學系統波前檢測數據的穩定性，通過動態干涉儀對光學系統波前進行多次累加測量。保持圖8中所示光路不變，分別在風扇開啟和風扇關閉兩種條件下對系統波前進行測量，每種條件下各測得10組數據，每組數據均包含500次原始數據的累加。在上述兩種條件下，干涉儀的數據采集模式、曝光時長、Mask大小，以及干涉儀、次鏡和三鏡調整臺的位姿等均保持一致，且所有數據均在同一天測得。實驗結果如圖9所示，圖中給出了Z5～Z16在不同環境條件下的穩定性。顯然，圖9（a）數據的穩性明顯好于圖9（b）。對兩種環境條件下的數據進行統計計算，各項條紋Zernike系數的標準差如表1所示。在主動隨機送風條件下，Z6～Z16的標準差在0.003以下，Z5的波動稍大，但也小于0.01。作為比較，關閉風扇后，保持光路其他元件、參數不變，Z5標準差增大了近4倍，達到0.037，其他各階Zernike系數的穩定性也明顯變差。上述數據充分證明，通過主動隨機送風，可以有效抑制大口徑、長焦距干涉檢測光路的氣流擾動，大幅度提高波前檢測的穩定性。

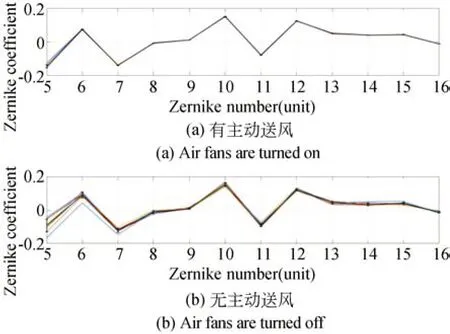
圖9 不同條件下的自準直干涉光路波前檢測結果穩定性Fig.9 Stability of wavefront measurement results of selfcollimating inteference optical system in different conditions

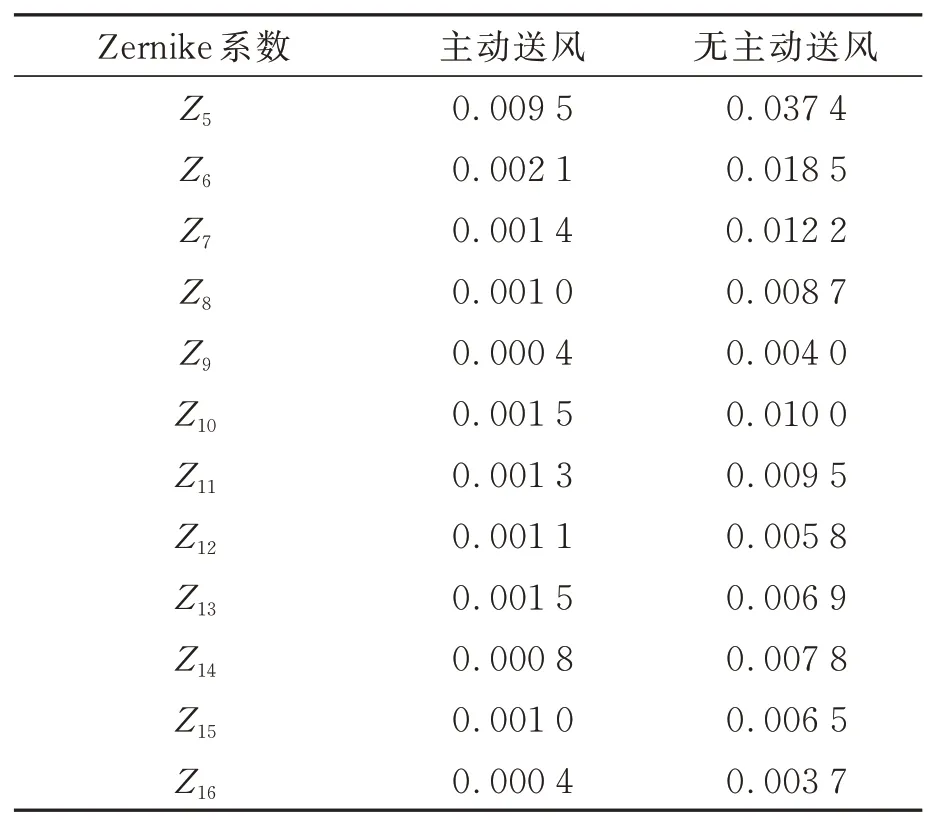
表1 不同測試條件下的條紋Zernike系數標準差Tab.1 Standard deviations of fringe Zernike coefficients under different measuring conditions

上述測試結果驗證了數據的穩定性，還需要進一步驗證數據的正確性。若上述波前檢測結果是由風扇送風而額外生成的，那么波前數據必然和風扇的設置密切相關，尤其是風扇的位置和朝向。因此，人為地改變光路中的風扇朝向和位置，如圖10所示，風扇陣列處于3種不同的組合狀態。在這3種狀態下，保持光路中其他參數和元件不變，采集系統波前數據，結果如圖11所示。可以發現，盡管風扇陣列的設置發生了很大變化，但是3種情況下波前檢測結果幾乎沒有區別，Z6和Z7的平均值也非常接近，如表2所示。圖12給出了3種不同風扇陣列設置情況下Z5～Z36的變化情況，可以看出，所有的Zernike系數在不同的風扇設置下基本一致。上述實驗結果表明，圖9和表1所示的波前檢測結果不隨風扇設置的不同而變化，能夠表征圖8中自準直干涉檢測光學系統的真實波前。

圖10 干涉檢測光路中三種不同的風扇組合Fig.10 Three different air fan combinations placed in inteference optical path

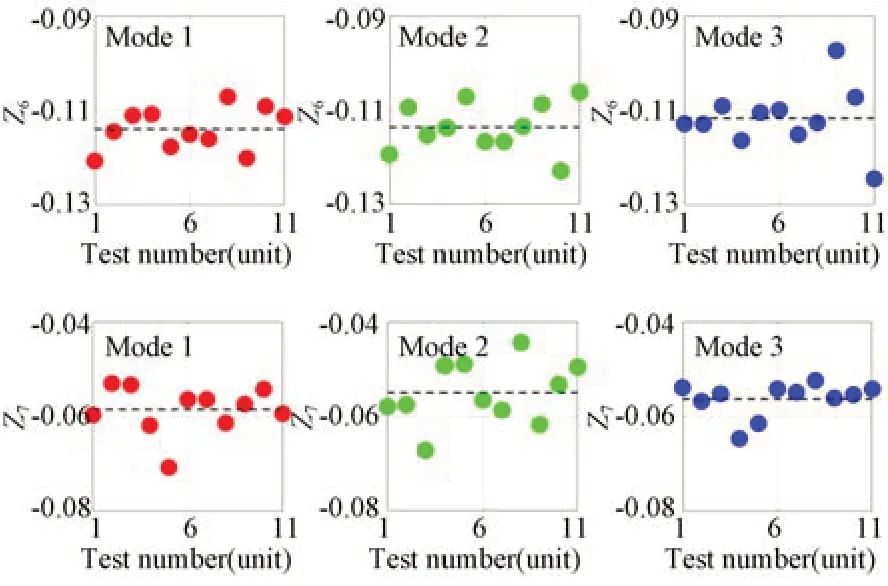
圖11 三種不同風扇組合下Z6和Z7的檢測結果Fig.11 Measured results of Z6 and Z7 under three different air fan combinations

表2 三種不同風扇組合下Z6和Z7的檢測結果平均值Tab.2 Mean values of Z6 and Z 7 with three different air fan combinations

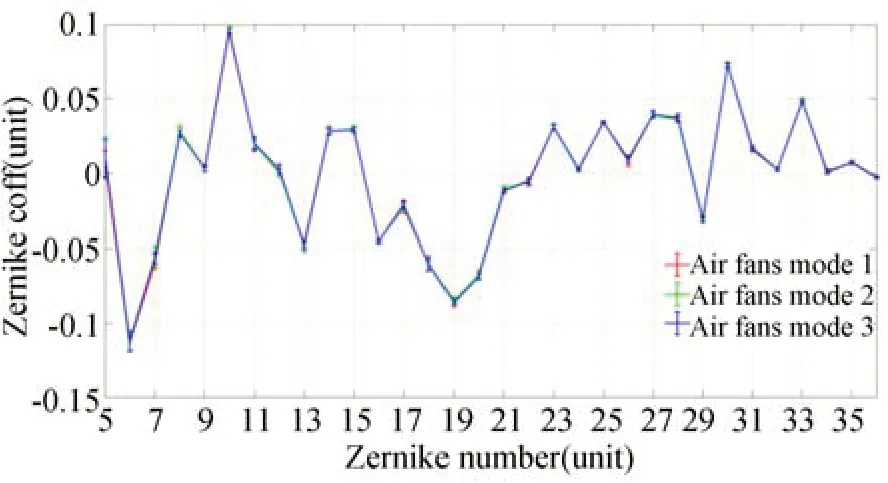
圖12 三種不同風扇組合下Z5～Z 36的檢測結果Fig.12 Measured results of Z5-Z 36 with three different air fan combinations

5 實驗與結果

由實測數據可知，通過主動隨機送風可以提高大口徑、長焦距干涉光路波前檢測結果的穩定性，并得到真實的系統波前結果。下面，我們將首次在主動隨機送風條件下，完成該離軸三反光學系統的計算機輔助裝調。

根據待裝調光學系統的特點，通過經緯儀和激光跟蹤儀完成系統粗裝調。將干涉儀和自準直平面反射鏡調整到位，經過一段時間連續主動隨機送風后，開始采集系統各個視場的波前數據，并保持系統一直處于主動隨機送風狀態。根據待裝調光學系統的視場離軸特點選定5個視場，包括4個邊緣視場和1個中心視場，如圖13所示。測得粗裝調完成后系統各個視場的波像差，如圖14所示。系統各視場波前RMS平均值為0.493λ。

圖13 計算機輔助裝調相關的5個視場Fig.13 Five fields of views used in computer-aided alignment

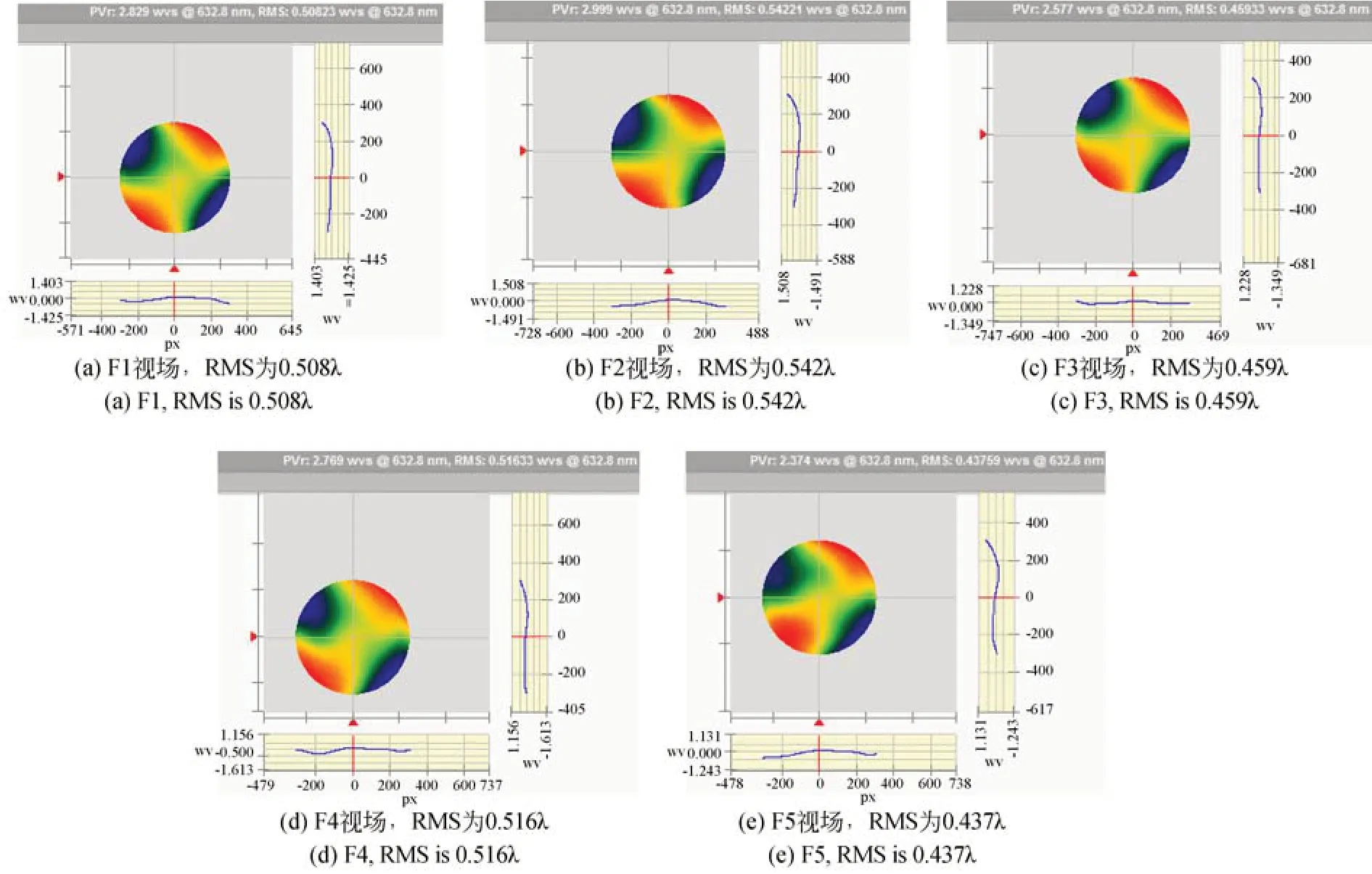
圖14 粗裝調結束后離軸三反光學系統5個視場的波像差檢測結果Fig.14 Measured wavefront errors over five different fields of views of off-axis TMA telescope after initial alignment

通過自編的計算機輔助裝調程序，根據測得的各個視場的Zernike系數，解算得到次鏡和三鏡的失調量，再通過次鏡和三鏡底部的六足臺調整次鏡和三鏡的位姿。調整完成后，再次檢測各個視場的波像差，波前檢測結果如圖15所示。各視場波像差RMS平均值降為0.094λ。顯然，系統各個視場的波像差明顯收斂，表明失調量解算結果正確。根據該輪檢測結果，又解算得到一組次鏡和三鏡的失調量，再次調整后，檢測得到各個視場的波像差如圖16所示，條紋Zernike系數如表3所示。各視場波像差RMS平均值進一步降為0.086λ，達到該系統的裝調指標要求。

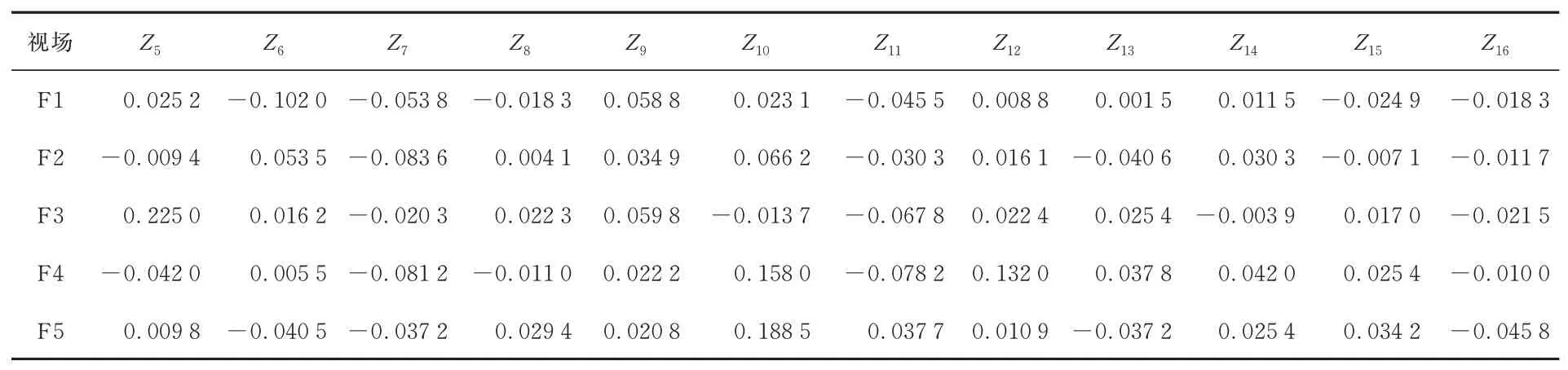
表3 兩輪計算機輔助裝調后系統各個視場條紋Zernike系數Tab.3 Measured fringe Zernike coefficients over five different fields of views of off-axis TMA telescope after second round CAA

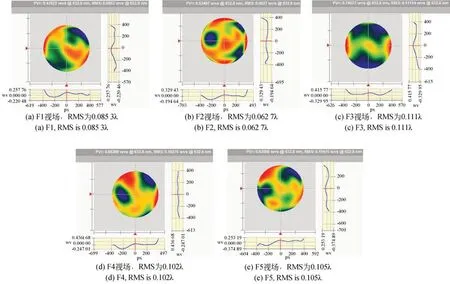
圖15 第一輪計算機輔助裝調后系統5個視場的波像差檢測結果Fig.15 Measured wavefront errors over five different fields of views of off-axis T MA telescope after first round CAA

圖16 第二輪計算機輔助裝調后系統5個視場的波像差檢測結果Fig.16 Measured wavefront errors over five different fields of views of off-axis TMA telescope after second round CAA

6 結 論

本文提出主動隨機送風的方案來抑制氣流擾動對大口徑、長焦距干涉光路波前檢測的影響。結合仿真結果和多次實驗迭代，優化了風扇陣列的數量、位置、朝向和風速等風場設置，使得通過主動隨機送風可以實現對大口徑、長焦距干涉光路溫度場和折射率場的擾動隨機化。測試結果表明，通過主動隨機送風可以顯著提高系統波前檢測結果的穩定性，Zernike系數標準差由0.04降低到0.01以下。最后，在主動隨機送風條件下，對一個6 m焦距、0.5 m通光口徑的離軸三反消像散光學系統進行了裝調。實驗結果顯示，在穩定的Zernike系數檢測結果下，通過一輪計算機輔助裝調，系統各個視場的波像差RMS平均值由0.49λ降低到0.094λ；兩輪裝調后系統各視場波像差RMS平均值達到0.086λ，滿足系統指標要求。由此表明，通過主動隨機送風，可以以極低的成本為大口徑、長焦距光學系統提供穩定、可靠的波前檢測環境，這對于大口徑光學系統的研制及應用具有重要意義。