西西弗斯數學黑洞的分析和研究

王德貴

大家知道宇宙中有一種叫“黑洞”的天體，它是由高密度物質組成，連光線射到這個天體上都能被吸收掉，不能被反射，黑洞的吸引力極其強大，使得視界內的逃逸速度大于光速，所以導致人們也看不見這個天體，所以稱它為黑洞，偷偷告訴大家一個小秘密，在瀏覽器中搜索黑洞詞條會有意想不到的結果，大家可以去試試。

關于“數學黑洞”的研究我們已經發了多篇文章，相信大家對數學黑洞已經有了一個較為深刻的理解，今天繼續用Python和Scratch來分析和研究這個著名的西西弗斯數學黑洞——123。

程序涉及的主要是等級考試4級內容——自定義函數。

一、 創意來源

數學黑洞123，又稱為西西弗斯串。將一個多位數的偶數個數、奇數個數和總個數排列在一起，結果永遠是“123”。其運算過程如下。

我們首先任取一個數，如81872115378，其中偶數個數是4，奇數個數是7，共11位數，這樣可以獲得一個新的數4711。該數有1個偶數，3個奇數，是4位數，又組成新數134。重復以上過程，1個偶數，2個奇數，是3位數，便進入了123這個數學黑洞。這時繼續重復以上程序，結果始終是123，再也逃不出去，像不像陷入了一個黑洞。

為什么把數學黑洞123叫西西弗斯串呢？因為在希臘神話中西西弗斯觸犯了眾神，諸神為了懲罰西西弗斯，便要求他把一塊巨石推上山頂，而由于那巨石太重了，每每未上山頂就又滾下山去，前功盡棄，于是他就不斷重復、永無止境地做這件事，西西弗斯的生命就在這樣一件無效又無望的勞作當中慢慢消耗殆盡，永無休止。這和數學黑洞123非常類似，因此，人們把123黑洞叫作西西弗斯串。

此前，美國賓夕法尼亞大學數學教授米歇爾·埃克先生僅僅對這一現象作過描述介紹，當時未能給出令人滿意的解答和證明。

我們已經知道了這條規則，那么是不是所有的數字這樣運算后都能獲得同樣的結果呢？有沒有例外呢？如何證明？下面我們仔細分析一下這條規則在不同情況下的表現：

（1）當目標是一個一位數時，如是奇數，則k=0，n=1，m=1，組成新數011，有k=1，n=2，m=3，得到新數123;

如是偶數，則k=1，n=0，m=1，組成新數101，又有k=1，n=2，m=3，得到123。

（2）當是一個兩位數時，如是一奇一偶，則k=1，n=1，m=2，組成新數112，則k=1，n=2，m=3，得到123;

如是兩個奇數，則k=0，n=2，m=2，組成022，則k=3，n=0，m=3，得303，則k=1，n=2，m=3，也得123;

如是兩個偶數，則k=2，n=0，m=2，得202，則k=3，n=0，m=3，由前面亦得123。

（3）當是一個三位數時，如三位數是三個偶數字組成，則k=3，n=0，m=3，得303，則k=1，n=2，m=3，得123;

如是三個奇數，則k=0，n=3，m=3，得033，則k=1，n=2，m=3，得123;

如是兩偶一奇，則k=2，n=1，m=3，得213，則k=1，n=2，m=3，得123;

如是一偶兩奇，則k=1，n=2，m=3，立即可得123。

（4）當是一個M（M>3）位數時，則這個數由M個數字組成，其中N個奇數數字，K個偶數數字，M=N+K。

由KNM連接生產一個新數，這個新數的位數要比原數小。重復以上步驟，一定可得一個三位新數knm。

以上僅是對這一現象產生的原因，簡要地進行分析，若采取具體的數學證明，演繹推理步驟還相當繁瑣和不易。直到2010年5月18日，關于“123數學黑洞（西西弗斯串）”現象才由中國回族學者秋屏先生作出嚴格的數學證明，并推廣到六個類似的數學黑洞（“123”、“213”、“312”、“321”、“132”和“231”），有足夠基礎的同學可以查查他的論文《“西西弗斯串（數學黑洞）”現象與其證明》。自此，這一令人著迷的數學之謎已被徹底破解。

二、 設計思路

數學黑洞有一個特點，即每次迭代計算的規則是一樣的，通過這樣簡單地重復一個規則，得到驚人的結果。

通過輸入一個多位正整數，判斷偶數個數、奇數個數和總個數，3個數字重組，形成新的多位正整數，再重復上述過程，最后得到123。因此我們先定義一個計算個數的自定義函數，每次調用即可。

然后再定義一個循環調用計算過程的自定義函數，直到結果為“123”。

三、 Scratch程序設計

想通過Scratch去實現這個程序，需要掌握判斷奇數和偶數的方法，任何數除以2余數為0的是偶數，為1的是奇數。還需要掌握變量、循環、判斷、運算符等。

創建四個變量：奇數個數（統計數字中奇數的個數）、偶數個數（統計數字中偶數的個數）、變量n（統計數字個數）、變量結果（存放每次新產生的數字）。

程序開始運行后用戶向系統輸入任意整數（不論長度和大小），將輸入的數字保存到列表中，并且增加控制循環變量的條件，只有最終得到結果為123時才可跳出循環，否則的話需要將保存在列表中的數字進行規定的變化。

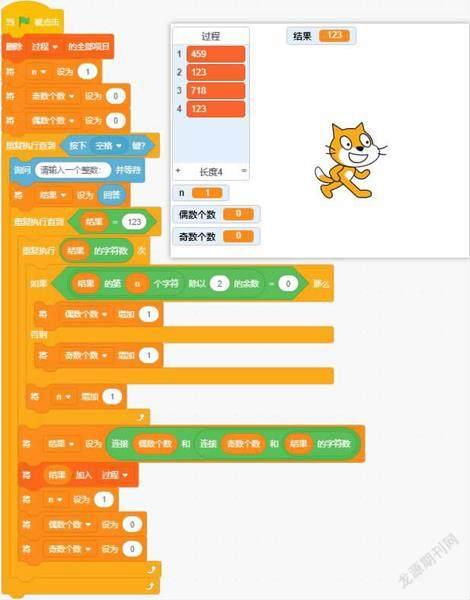
首先通過提取判斷的方法，獲得列表中數字的偶數位、奇數位、總位數的數字，將三個數進行拼接得到一個新的結果，并將其保存入列表中，將新的結果與數字123進行比較查看是否相等，若不相等繼續對新數字做相同的處理，直到最終的結果等于123結束（圖1）。

四、 Python程序設計

有了Scratch的基礎，Python程序設計也不是很難，語句很好理解。一是奇數和偶數的判斷，然后分別添加到相應的列表中，再計算總位數。

然后根據輸入的多位數，調用運算函數，得到新的多位數，再調用運算函數，直到結果為“123”（圖2）。

輸入多位數，驗證結果，均為黑洞“123”（圖3）。

五、測試與改進

其實這個程序也可不用自定義函數，一樣可以完成驗證。

這個黑洞算法的基礎上，我們最后再加一條規則，奇偶個數之差（取絕對值），是不是也會出現數學黑洞，這個黑洞還是“123”嗎？（圖4）

修改上述程序，即可看到，最后重復出現的數是“4044”，我們找到了一個新的數學黑洞（圖5）。

通過運行修改后的程序，發現“4044”是新黑洞。前面是按“偶奇和差”的順序排列，如果按“偶奇差和”排列呢？還會是“4044”嗎？（圖6）

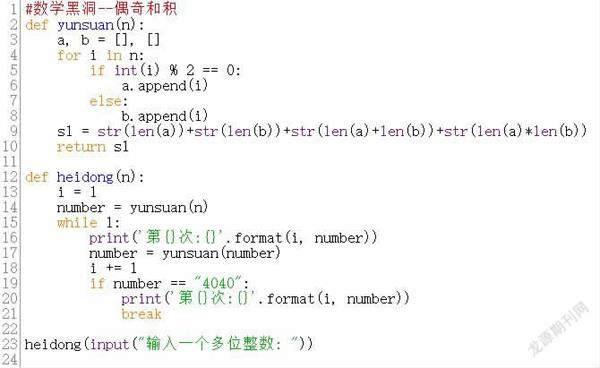
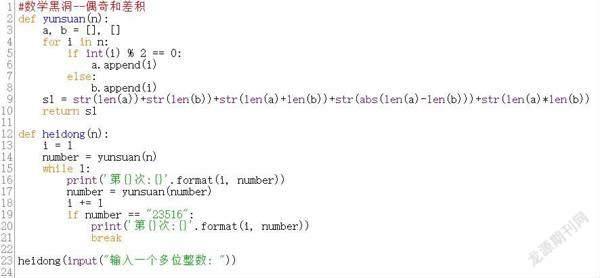
對這個程序有興趣的朋友可以自己去驗證一下。那么按“偶奇和積”排列，或按“偶奇和差積”排列，還有數學黑洞嗎？（圖7、圖8）

這樣看來，一定還有很多數學黑洞沒有被發現……

本文也是我自己的心得，有不妥之處，請各位同仁斧正！