低軌星座系統的可控波束到地功率通量密度研究

黃穎，李偉，簡晨，嚴康

（國家無線電監測中心，北京 100037）

0 引言

近年來，在Google、Amazon和SpaceX等科技巨頭公司的推動和支持下，衛星互聯網行業迅速發展，旨在為全球用戶提供不間斷的寬帶互聯網接入服務，誕生了一批以Starlink、OneWeb和O3b為代表的低軌星座系統[1-2]。低軌星座通信被認為是融合到未來6G之中，實現全球立體泛在覆蓋的重要技術[3]。目前，全球公開發布的低軌通信星座系統計劃有20多個，其中OneWeb公司申請發射約4.8萬顆衛星，SpaceX公司申請發射約4.2萬顆衛星[4]。這些星座系統通常具有衛星規模龐大、軌道高度低、波束寬度窄、波束可控等特征，且使用頻率集中，都計劃使用Ku/Ka/Q/V頻段資源，低軌星座系統之間發生有害干擾的概率極大[5]。同時，在這些頻段運行著大量靜止軌道衛星通信系統，低軌星座系統很有可能會對使用相同頻率的其他空間或地面通信系統造成有害干擾[6-8]。

為保護以同等權利共用頻段的固定業務或移動業務，《無線電規則》第21.16條中規定了空間電臺發射到地球表面的功率通量密度（power flux-density，PFD）的限值[9]。新興的低軌星座系統的星座構型復雜，星座規模從幾十顆到幾百顆甚至上千顆不等，覆蓋特性能夠滿足全球任何地點[10]。這些新興的低軌星座系統采用相控陣天線技術、新型頻率復用技術、星上處理技術、功率控制技術、動態頻譜共享技術等多種關鍵技術[11]，其用戶波束和饋電波束多為可控波束[12]。新興的低軌星座系統衛星到地的PFD計算需要考慮不同可控角的發射功率和天線參數特性，同時低軌星座系統在Ka/Q/V等頻段的PFD限值需考慮星座規模。因此有必要對低軌星座系統可控波束到地PFD計算方法和PFD限值符合性判定方法進行研究。

1 可控波束到地PFD計算方法

《無線電規則》第21.16條中規定，空間電臺到地產生的最大PFD不應超過相應業務及頻段的限值。這個最大PFD是在自由空間傳播條件下獲得的。PFD的定義為單位面積通過的功率，因此計算空間電臺在地球表面產生的最大PFD需要確定與發射功率和傳播距離兩個參數相關的變量，如發射功率譜密度、天線方向圖和不同仰角傳播距離等。空間電臺對地發射示例如圖1所示，空間電臺信號到達地球站所在點的方向與水平面夾角定義為對地到達角θ（即仰角），空間電臺到地球站與空間電臺到地心的夾角定義為半視角φ。設地球半徑為R，衛星與地球站之間的傳播距離L和半視角φ可表示為：

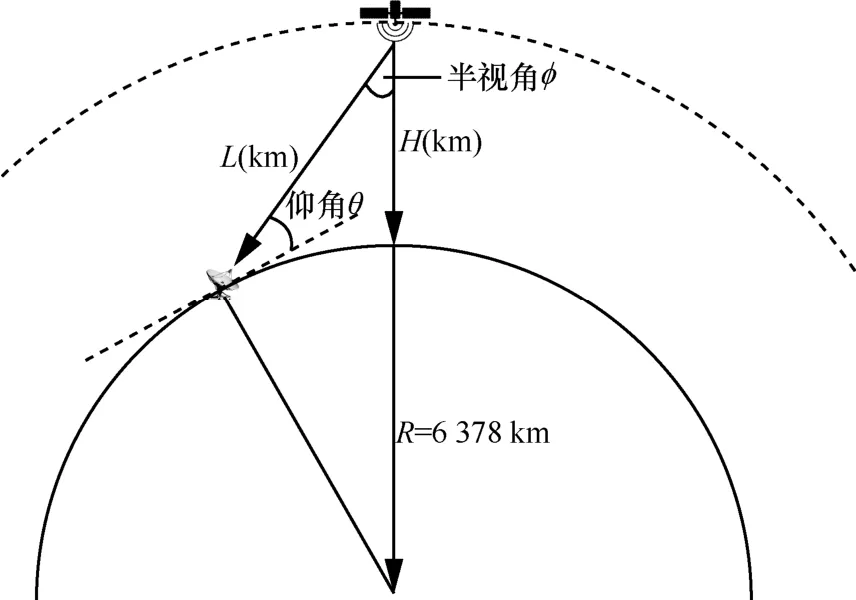
圖1 空間電臺對地發射示例

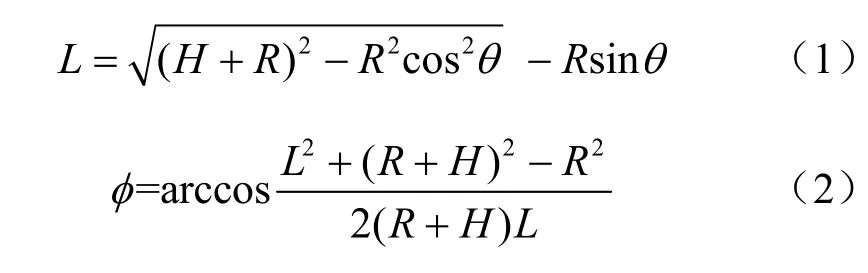
由式（1）、式（2）可知，衛星與地球站之間的傳播距離、半視角均與仰角、衛星軌道高度有關。對于低軌星座系統可控波束，當波束指向觀察點時，衛星天線可控角正好等于半視角。可控波束通過相控陣天線或機械轉動天線實現。若衛星天線為相控陣天線，天線總增益為陣列增益 AG與單元增益 eG之和，陣列增益與單元增益組合形成的相控陣天線方向示意圖如圖2所示[13]，可知不同可控角時天線最大增益Gmaxφ()不同。若衛星天線為機械轉動天線，不同可控角最大增益Gmax相同。可控角為φ時的衛星發射功率譜密度P()φ由衛星系統本身決定。比如，Starlink系統采用相控陣天線，通過功率控制算法實現可控波束在不同對地到達角情形的最大PFD恒定不變[14]，此時發射功率譜密度P()φ主要由天線增益G()φ和星地傳播距離L決定。計算空間電臺可控波束在不同水平面到達角θ時的最大PFD，需要獲取以下參數信息：可控角φ時的最大發射功率譜密度Pmax()φ、可控角φ時水平面到達角θ方向對應發射天線離軸角ψ、與可控角φ和離軸角ψ相關的天線增益G(φ,)ψ、傳輸距離L()θ。可控波束的最大PFD計算式如下：

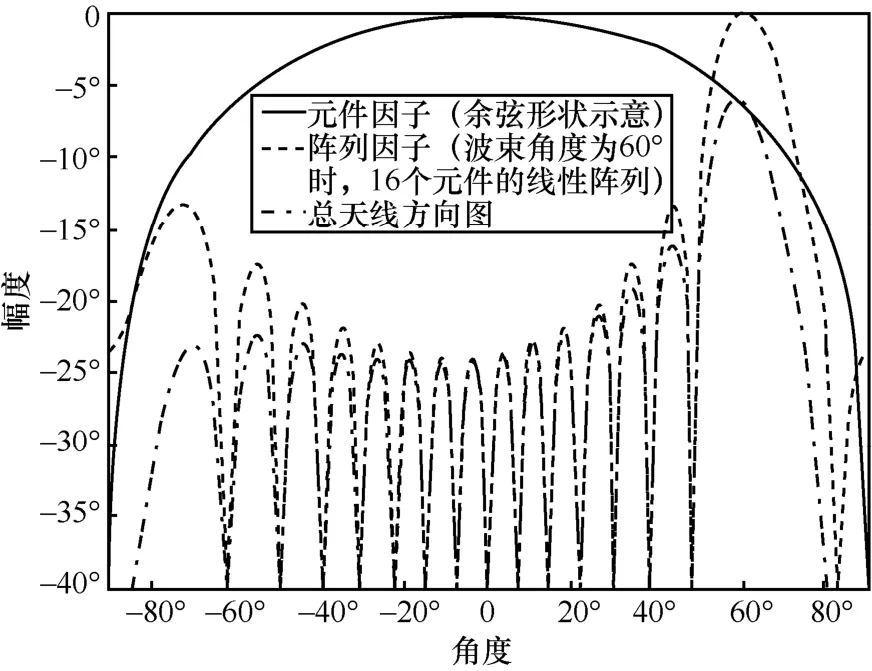
圖2 陣列增益與單元增益組合形成的相控陣天線方向示意圖

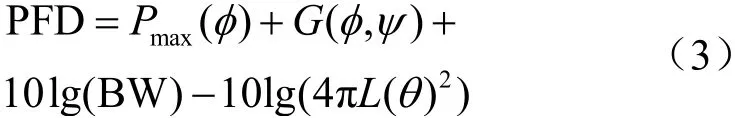
當已知不同可控角φ時對應的最大等效全向輻射功率（equivalent isotropically radiated power，EIRP）譜密度 EIRPmax(φ)，可控波束的最大PFD計算式如下：

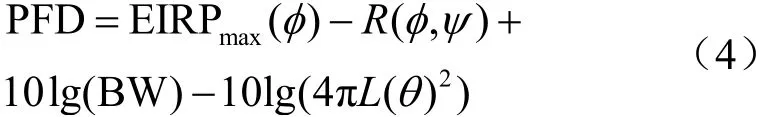
其中，BW通常定義為《無線電規則》第21.16條中限值對應的參考帶寬，即為4 kHz或1 MHz。R(φ,ψ) =G(φ, 0)?G(φ,ψ)為離軸角ψ時相對最大增益的下降量，ψ=0時R(φ,ψ) =0，在半功率波束寬度處時，R(φ,ψ) =3dB 。

下面分析離軸角ψ的取值范圍。不同可控角時到地PFD示意圖如圖3所示，地球站A處觀察點水平面上到達角為θ。衛星可控波束指向地球站A時，此時可控角等于半視角，均為φ1，A處離軸角ψ1為0，觀察點方向上天線增益為衛星最大發射功率譜密度為Pmax(φ1)。衛星可控波束指向地球站B時，可控角為φ2，地球站A處觀察點離軸角為ψ2，觀察點A方向上衛星天線增益為G(φ2,ψ2)，衛星最大發射功率譜密度為Pmax(φ2)。

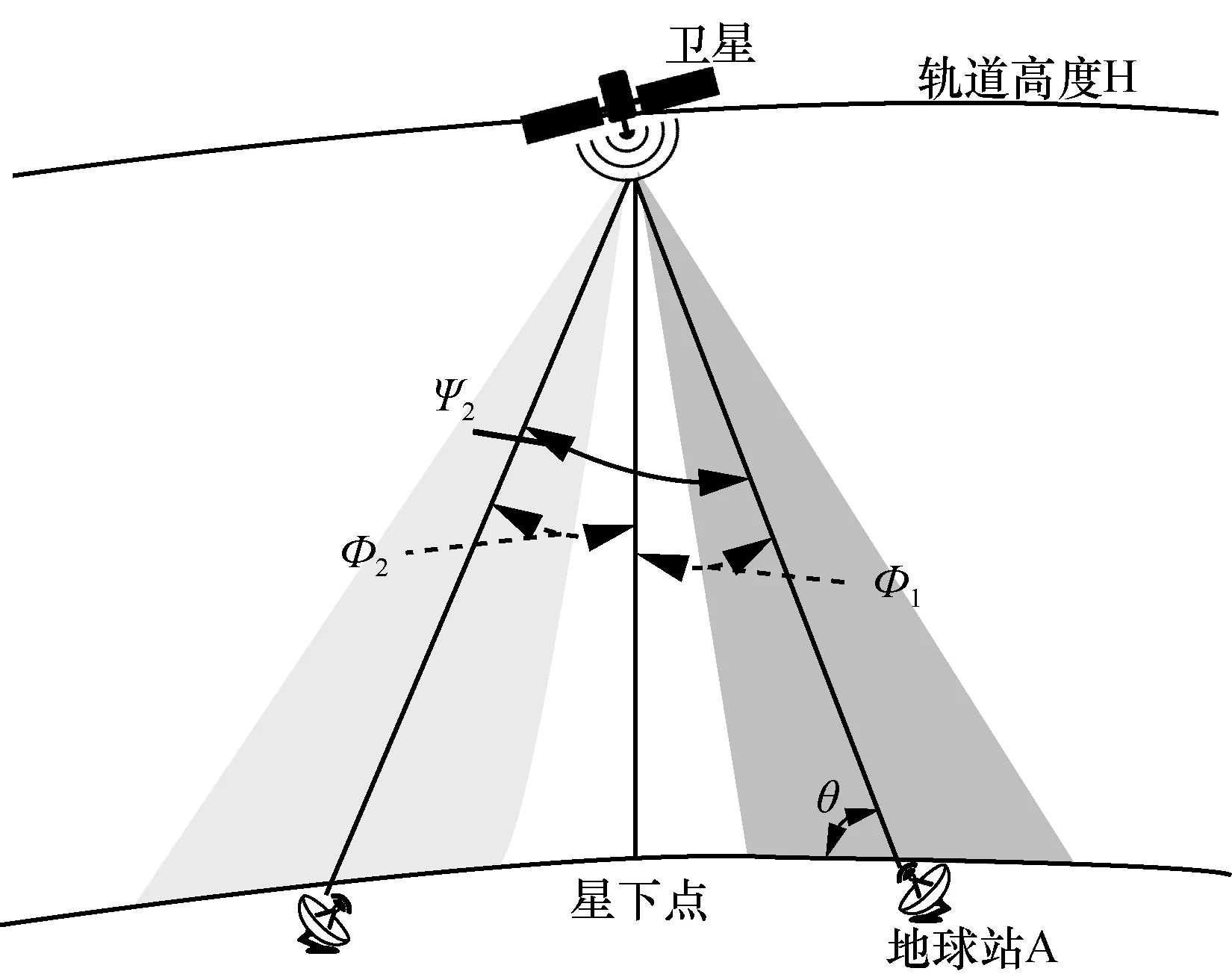
圖3 不同可控角φ時到地PFD示意圖

離軸角ψ2的大小由可控角φ1和φ2共同決定，且 |φ1?φ2|≤ψ2≤φ1+φ2。具體說明如下。

離軸角的取值范圍示意圖如圖4所示，衛星星下點為O，可控角為1φ時，波束中心在地面點的集合為圖4中小圓，此時指向A點。可控角為2φ時波束中心在地面點的集合為圖4中大圓，此時指向B’點，A處觀察點離軸角 2ψ的大小根據B’的位置變化而變化。三角形AOB’中，AO和B’O為固定長度，AB’長度取決于∠B’OA。當B’運動到B點時，AB’最小，對應離軸角ψ2=|φ2?φ1|；當B’運動到B”處時，AB’最大，對應離軸角ψ2=φ2+φ1。因此有 |φ1?φ2|≤ψ2≤φ1+φ2。

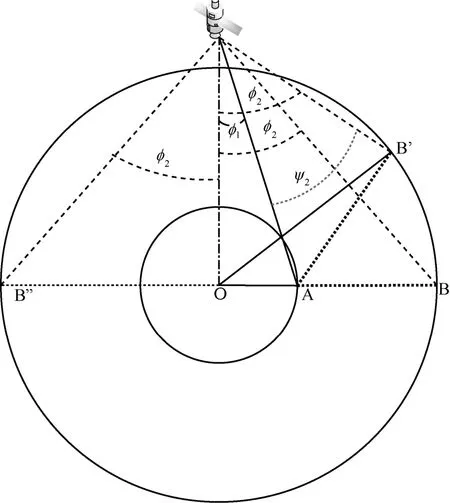
圖4 離軸角的取值范圍示意圖

2 可控波束PFD限值符合性判定方法

通過式（3）或式（4）可計算特定可控波束到地PFD值。按照國際電信聯盟規定，評判特定可控波束到地PFD值是否滿足《無線電規則》第21.16條限值要求，除了分析評估該特定可控波束在覆蓋范圍內是否滿足限值要求之外，還需要同時判斷可控波束覆蓋范圍之外的PFD值是否滿足限值要求。

2.1 特定可控角下可控波束PFD限值符合性判定算法

當衛星天線參數確定后，可控波束最大發射功率譜密度Pmax(φ)或最大 EIRP譜密度EIRPmax(φ)便可確定。可控角固定時到地PFD示意如圖5所示，可控角為φ的可控波束指向觀察點A，判斷該可控波束是否滿足PFD限值要求，應計算此可控波束對任意水平面上到達角θ產生的PFD均能滿足限值要求，具體算法步驟如下。

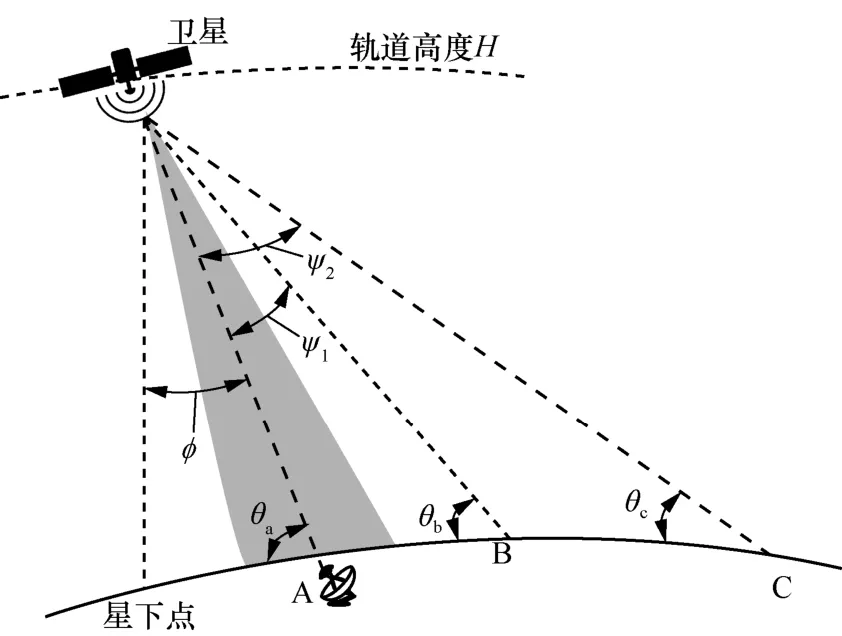
圖5 可控角φ固定時到地PFD示意圖

步驟1?θ∈ (0,90]，利用式（3）或式（4）計算到地PFD(θ)。

步驟2?θ∈ (0,90]，按照《無線電規則》第21.16條要求計算相應業務相應頻段PFD限值PFDLimit(θ)。

步驟3如果?θ∈ (0,90], PFD(θ)> PFDLimit(θ)，則可控角為φ的可控波束不滿足PFD限值的要求；如果?θ∈ (0,90]，均有 PFD(θ) ≤PFDLimit(θ)，則可控角為φ的可控波束 EIRPmax(φ)）滿足限值要求。

可控角為φ的可控波束不滿足PFD限值時，則應減小衛星的發射功率譜密度Pmax(φ)或EIRP譜密度 EIRPmax(φ)，使其滿足?θ∈ (0,90]，均有PFD(θ) ≤PFDLimit(θ)。將式（3）或式（4）代入，則?θ∈ (0,90]，

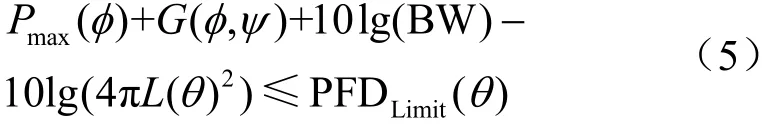
或

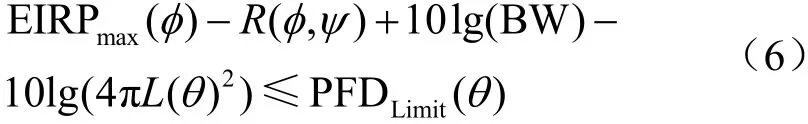
式（5）和式（6）變換后，在可控角為φ時的衛星最大發射功率譜密度Pmax(φ)或最大EIRP譜密度 EIRPmax(φ)，可由式（7）、式（8）確定：

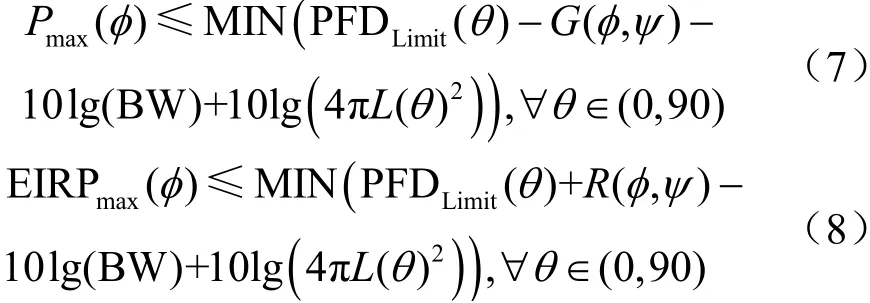
2.2 基于仰角遍歷的可控波束PFD限值符合性判定算法

基于第3.1節給出的特定可控角下的可控波束PFD限值符合性判定方法，遍歷可控波束的可控角φ取值范圍，即可分析可控波束是否滿足PFD限值要求。這種方法思路較為簡單，但需要執行每個可控角下不同仰角PFD的符合性判定，運算復雜度高。本節將給出基于仰角遍歷的可控波束PFD限值符合性判定方法，先在給定仰角下從所有的可控波束找到最大PFD，然后再與限值作比較，無須判定每個特定可控角的可控波束是否滿足PFD限值要求。可控波束不同到地角最大PFD計算流程如圖6所示，具體的算法步驟如下。

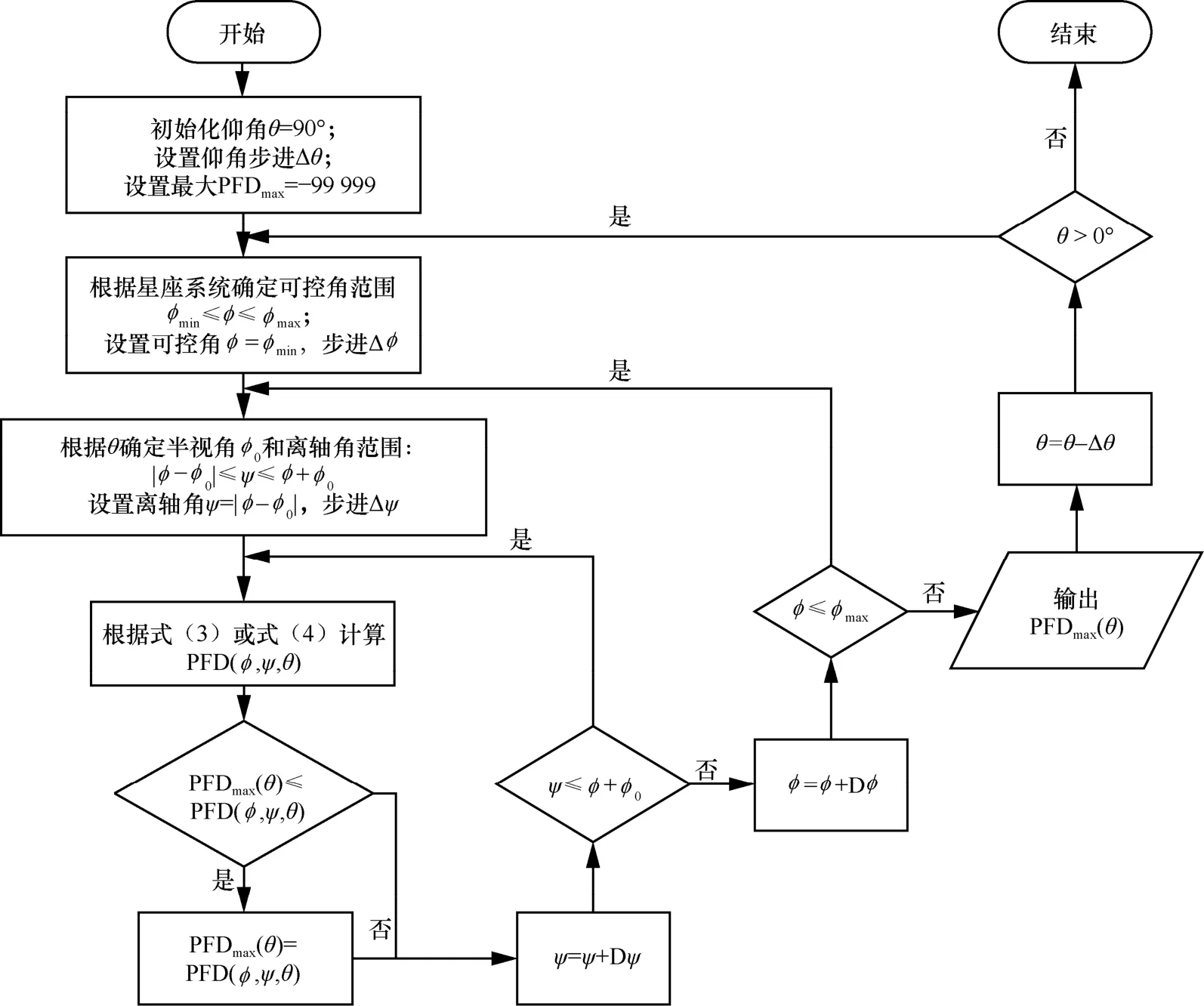
圖6 可控波束不同到地角最大PFD計算流程

步驟1根據低軌星座系統信息獲取不同可控角的功率譜密度Pmax(φ)或EIRP譜密度EIRPmax(φ)、天線方向圖、最大增益和波束可控范圍（根據系統最低通信仰角確定）等信息。

步驟2初始化仰角θ=90°，設置仰角遍歷步進為 Δθ，初始化 PFDmax(θ)=?9 999。

步驟3初始化可控角φ=φmin，設置可控角遍歷步進為 Δφ，根據仰角計算半視角φ0。

步驟4初始化離軸角ψ=|φ?φ0|，設置離軸角遍歷步進為 Δψ。

步驟5利用式（3）或式（4）計算當前仰角、可控角和離軸角下的可控波束到地PFD(φ，ψ，θ)。

步驟6若 PFD (φ，ψ，θ) ≥ PFDmax(θ)，則PFDmax(θ)=PFD(φ，ψ，θ)，否則直接進入下一步。

步驟7離軸角ψ=ψ+ Δψ（不同離軸角對應指向不同但可控角相同的可控波束）。

步驟8若離軸角小于φ+φ0，重復步驟（5）至步驟（7），否則進入步驟（9）。

步驟9可控角φ=φ+ Δφ。

步驟10若可控角φ小于最大值φmax，重復步驟（4）至步驟（9），否則進入步驟（11）。

步驟11輸出 PFDmax(θ)，此時得到仰角為θ時可控波束到地的最大PFD。

步驟12仰角 =θθ?θΔ ；

步驟13若仰角θ大于0°，重復步驟（3）～步驟（12），否則結束。

通過以上步驟，便可確定低軌衛星可控波束在不同對地到達角θ的最大功率通量密度PFDmax(θ)，與相應的限值 PFDLimit(θ)對比后，如果?θ∈ (0,90]， PFDmax(θ)>PFDLimit(θ)，則該可控波束不滿足PFD限值的要求；如果?θ∈ (0,90]，均有 PFDmax(θ) ≤PFDLimit(θ)，則該可控波束滿足限值要求。

2.3 低軌星座系統可控波束最大PFD簡化算法

利用第3.2節的算法求解低軌星座系統可控波束在不同仰角最大PFD需進行離軸角、可控角和半視角三重遍歷循環，運算量仍較大。低軌星座系統使用的頻段較高，其可控波束通常為高增益窄波束，在主瓣外增益迅速下降。一般來講，對某一觀察點，可控波束直射（主瓣作用）產生的PFD比未直射（旁瓣作用）產生的PFD大。若此條件對任意觀察點均成立，則只需要計算波束直射觀察點的PFD便可得到該仰角的最大PFD。下面對兩個可控波束直射觀察點和未直射觀察點產生的PFD進行比較分析。

可控波束覆蓋范圍示意圖如圖7所示，觀察點A處半視角為φ，仰角為Aθ。可控波束指向A時，可控角等于半視角φ，利用式（4）計算該點PFD時，R(φ,ψ)=R(φ, 0)=0。此時PFD為：

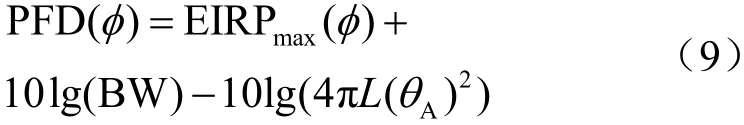
可控波束指向B點時，可控角為1φ，到觀察點A處的離軸角為 1ψ，PFD為：

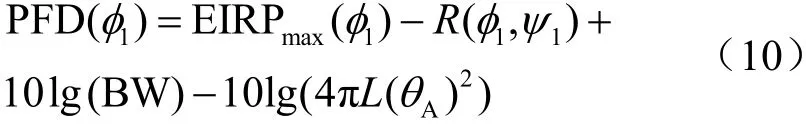
這兩個可控波束在A點產生的PFD的差值為：

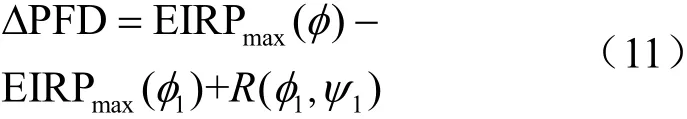
其中， |φ1?φ|≤ψ1≤φ1+φ。若 ?φ1∈ [φmin,φmax]，均 有 ΔP FD ≥0，即 EIRPmax(φ1)?EIRPmax(φ)≤R(φ1,ψ1)，則仰角為θA時對應的最大PFD產生于可控波束直接指向觀察點A。因此，當觀察點位于可控波束可覆蓋范圍內任意一點時，可控波束指向觀察點產生的PFD等于可控波束在對應仰角（該觀察點）產生的最大PFD需滿足的條件為：

其中，φ為任意觀察點處對應的半視角，φ1為任意可控角，ψ1為可控角為φ1的波束到觀察點處的離軸角，|φ1?φ|≤ψ1≤φ1+φ，Δ E IRPmax(φ1→φ)=EIRPmax(φ1)?EIRPmax(φ)，表示任意可控角φ1處的EIRP相對于可控角φ（也是半視角）時的EIRP的增量。

3 低軌星座系統可控波束到地PFD分析與驗證

SpaceX公司在2020年5月向美國聯邦通信委員會（Federal Communications Commission，FCC）提交了Starlink二代星座系統的申請[15]，擬發射30 000顆低軌衛星，申請使用Ku/Ka/E頻段，運行在328.3～614 km等8個不同軌道高度。用戶波束和饋電波束均為可控波束，采用相控陣天線[16]。本節以Starlink二代星座系統為例，分析計算Starlink可控波束PFD并驗證限值的規則符合性。

3.1 Starlink衛星可控波束特性分析

Starlink用戶波束和饋電波束均為可控波束，如圖7所示，地面加粗部分為可控波束覆蓋范圍，根據式（1）、式（2），可通過地面站最低通信仰角θ計算給定高度衛星的波束最大可控角φ。

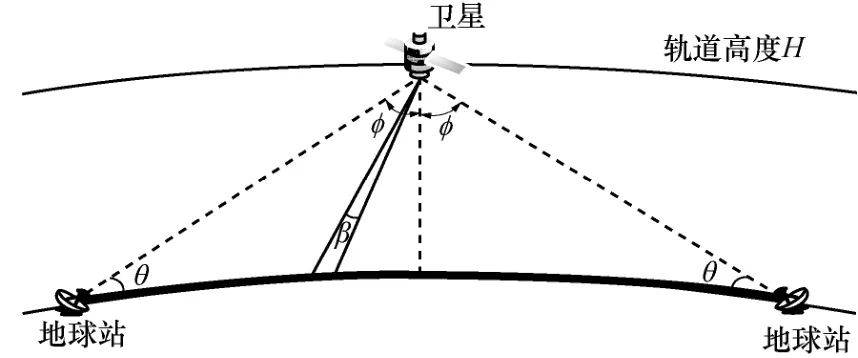
圖7 可控波束覆蓋范圍示意圖

對于360 km和373.2 km高度的衛星，位于高于緯度62°地區（極地地區）的信關站，Ka頻段饋電波束（下行17.8～18.6 GHz/18.8～19.3 GHz）和E頻段饋電波束（下行71～75 GHz）最低通信仰角為5°，緯度低于62°最低通信仰角為25°，其余軌道高度衛星饋電波束對應任何地區信關站最低通信仰角均為25°。不同軌道高度衛星饋電波束對應地球站最低通信仰角見表1。根據式（1）、式（2），360 km高度衛星不同最低仰角θ對應最大半視角φ和通信距離見表2。

表1 Starlink衛星饋電波束對應信關站最低通信仰角

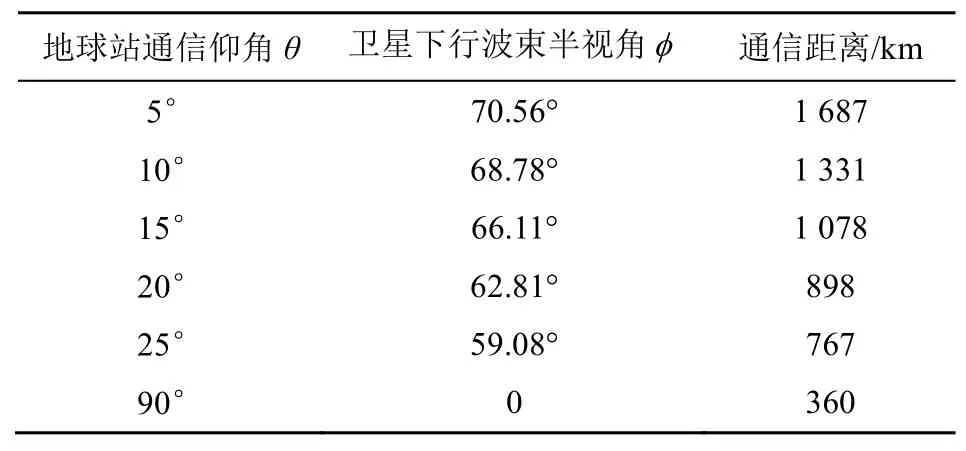
表2 360 km高度Ka/E頻段地球站通信仰角對應半視角

Starlink星座系統通過功率控制，使得可控波束到地PFD恒定不變，在可控角度覆蓋范圍內相同增益的地面站接收載波功率相同。波束可以大范圍轉動，Starlink衛星下行發射功率需根據不同可控角進行調整，以補償路徑損耗和發射天線增益變化引入的衰減變化。從圖8和圖9可知，360 km高度處，Ka頻段和E頻段饋電鏈路Starlink衛星EIRP譜密度隨可控角不斷增大而逐漸增大。在可控角增至約70.56°時，EIRP譜密度驟降。這是因為此時地球站仰角約為5°，剛好低于最低通信仰角。

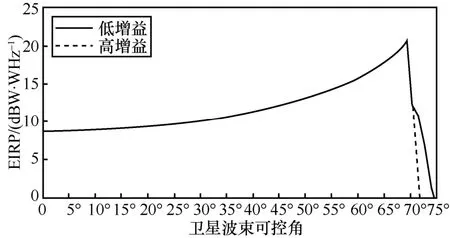
圖8 不同可控角對應的EIRP譜密度（Ka頻段）[13]

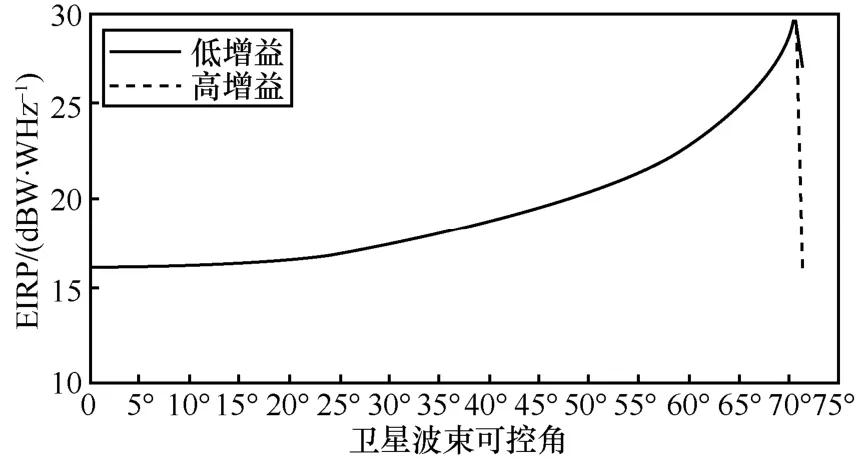
圖9 不同可控角對應的EIRP譜密度（E頻段）[13]

3.2 Starlink衛星可控波束最大PFD簡化算法適用性分析

Starlink可控波束天線為高增益天線，360 km高度Ka頻段衛星用戶波束的天線最大增益為34.5 dB或44.5 dB，E頻段衛星測控波束的天線最大增益為42 dB或52 dB。波束主瓣以外，天線增益迅速降低，R(φ,)ψ隨離軸角ψ增大而迅速變大，半功率波束寬度小于2°，離軸角為1°時，R(φ,ψ) =3 dB ；離 軸 角 為 約 3.5°時，R(φ,ψ) =20 dB[17]；離 軸 角 超 過 3.5°時，R(φ,ψ) >20 dB 。由圖8和圖9結合該波束相控陣天線離軸角ψ相對天線最大增益下降量R(φ1,ψ1)可知：

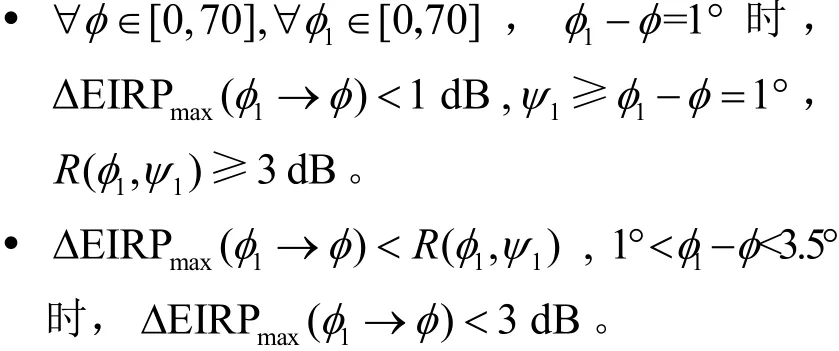
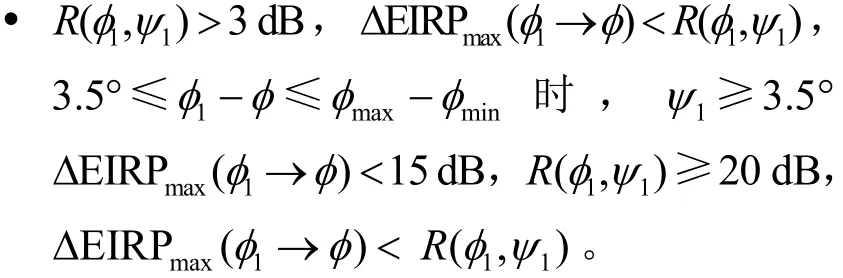
因此對任意觀察點位于可控波束覆蓋范圍內，均能滿足第3.3節中式（12）的要求。

由上述分析可知，針對Starlink星座系統的Ka/E頻段的饋電波束，計算不同仰角下最大PFD只需要分析可控波束指向觀察點時（可控角等于半視角）的情況，無須分析觀察點處于可控波束覆蓋范圍外的情況。

3.3 計算結果與分析

依據第4.2節的結論，分析Starlink衛星可控波束的發射是否滿足第21.16條PFD限值要求，只需要確定可控波束在不同水平面上到達角θ的最大功率通量密度 PFDmax(θ)和對應的限值 PFDLimit(θ)即可。

360km軌道高度處，Ka頻段Starlink衛星發射EIRP譜密度見表3[13]。根據式（1）、式（2）和式（4），可計算不同對地到達角時的最大 PFDmax(θ)，見表4。《無線電規則》第21.16條中17.7~19.3 GHz頻段非靜止軌道（non-geostationary satellite orbit，NGSO）星座系統PFD限值 PFDLimit(dBW/(m2?M Hz)?1)的計算見式（13），可知限值與NGSO星座系統規模有關。Starlink星座系統衛星顆數為30 000顆，因此N取30 000。

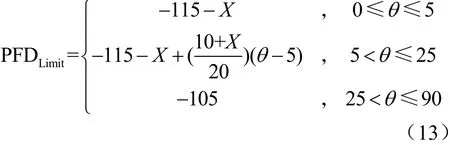
其中，

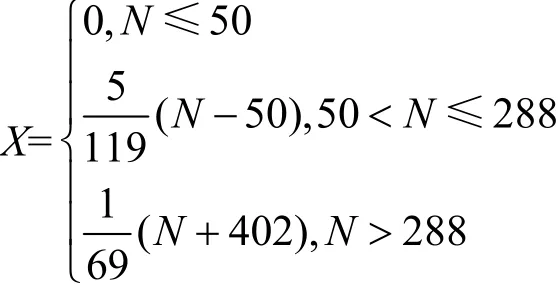
N為星座系統衛星數量。

360 km軌道高度處，E頻段下行波束，根據表2可得到不同地球站仰角的半視角，通過相應半視角在圖9查得相應的可控角對應EIRP譜密度的大約值，Ka頻段與E頻段EIRP譜密度見表3。利用式（4）計算得到最大PFD，與SpaceX核定值[14]均見表4。《無線電規則》第21.16條暫無E頻段的PFD限值。

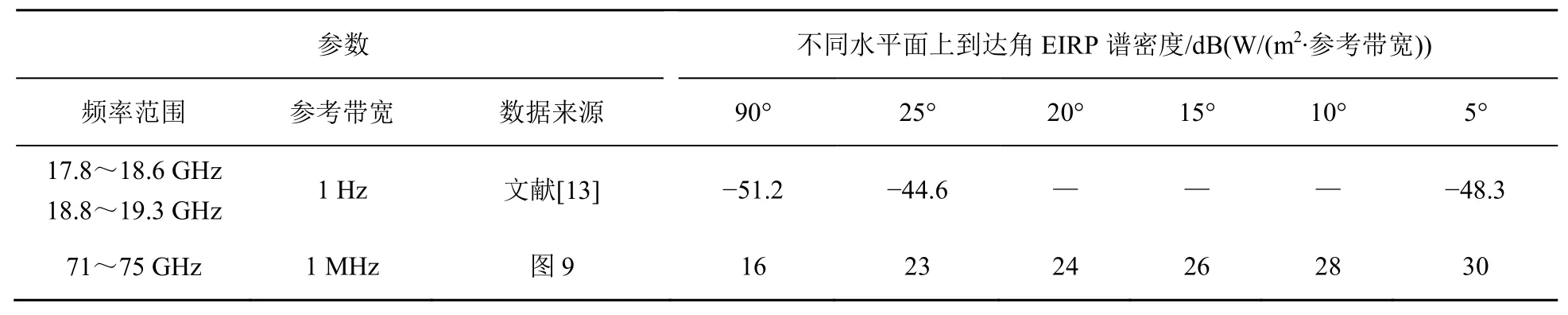
表3 Ka頻段與E頻段EIRP譜密度

根據表4可知如下內容。

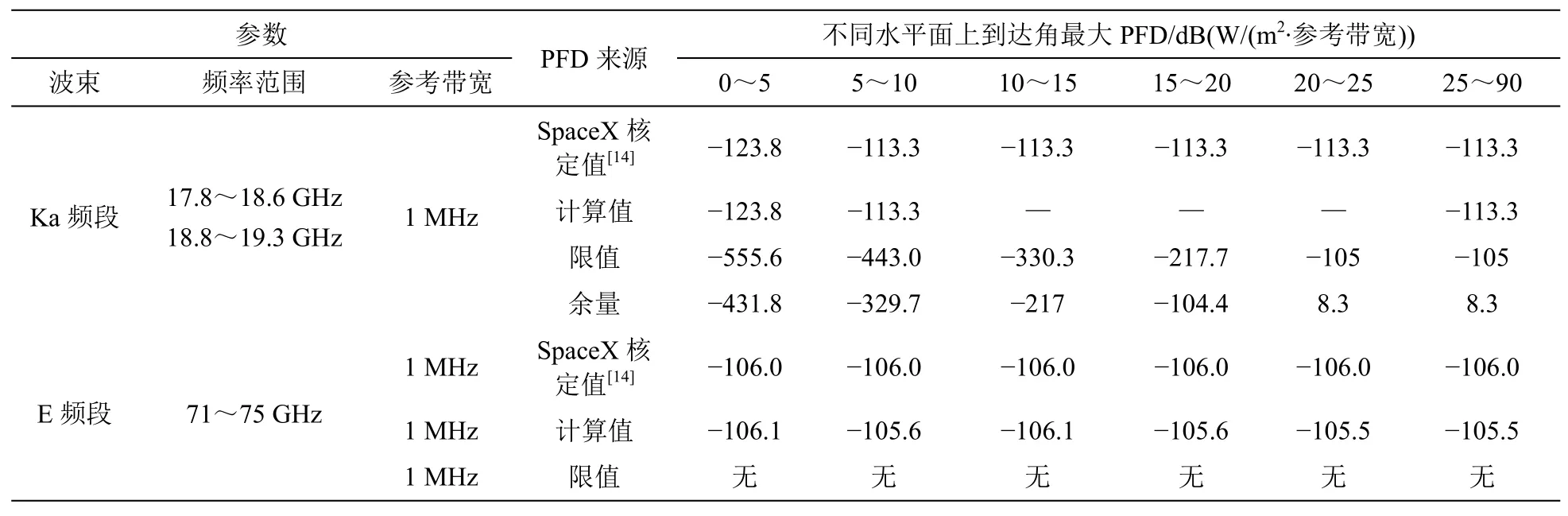
表4 360 km高度Ka/E頻段饋電可控波束水平面上到達角最大PFD與限值

· 在不同對地到達角下，所提方法分析得到的Ka頻段/E頻段可控波束到地最大PFD的計算值與SpaceX公司申請材料提供的計算值是一致的。

· 水平面到達角在20°以下時，Starlink星座系統的Ka頻段可控波束最大PFD遠大于《無線電規則》第21.16條規定的PFD限值，不滿足規則要求。

· 由于《無線電規則》第21.16條暫未規定E頻段的PFD限值，無法判定Starlink星座系統的E頻段測控波束是否會對固定業務系統/移動業務系統產生有害干擾。

對于不滿足限值的情況，SpaceX公司作出如下說明[13]：星座系統衛星數量多達30 000顆，式（13）中N為30 000，導致17.7～19.3 GHz的PFD限值在5°以下水平面上到達角時為?555.6 dB(W/(m2·MHz))，遠小于核定的最大PFD；用于Ka頻段的PFD限值計算方法是在低軌星座系統衛星數量很少時的研究周期制定的。對大型星座系統，這種計算方法大大高估了對地面固定業務系統產生有害干擾的可能性，不適用于衛星數量大于840顆的動態控制波束的低軌星座系統[18]；SpaceX公司申請豁免Ka頻段（17.8～18.6 GHz/18.8～19.3 GHz）的PFD約束[16]。

4 結束語

為保護頻率使用同等地位的固定業務和移動業務，ITU針對空間業務到地PFD提出了明確的限值要求。本文分析了低軌星座系統可控波束的PFD的計算方法，給出了特定可控角可控波束PFD限值符合性判定算法，基于此，提出了一種基于仰角遍歷的可控波束PFD限值符合性判定算法并給出了相應的算法流程。結合低軌星座系統特征，給出了可控波束最大PFD簡化算法。以Starlink星座系統可控波束為分析場景，計算分析了Ka/E頻段饋電波束的PFD。分析結果表明，所提可控波束PFD算法與Starlink系統使用方法得到的分析結果一致，印證了所提算法的有效性。Ka頻段饋電波束到地PFD在仰角低于20°時不滿足限值要求，主要原因在于《無線電規則》第21.16條中PFD限值大小與低軌星座系統衛星規模正相關。由于暫無PFD限值約束，無法判定Starlink系統E頻段饋電波束是否會對地面業務系統產生有害干擾。