均勻異號電荷等大共軸圓板軸線上電場均勻性研究*
周群益
(廣州理工學院通識教育學院 廣東 廣州 510540)
鐘 錚
(贛州市第一中學 江西 贛州 341000)
莫云飛
(長沙學院電子信息與電氣工程學院 湖南 長沙 410022)
侯兆陽
(長安大學理學院 陜西 西安 710064)
1 引言
對于均勻帶電圓形薄板,為了計算軸線上的電場強度,許多教材根據電勢疊加原理首先推導出電勢公式[1~4]

其中,σ是電荷的面密度,ε0是真空介電常數,R是圓板的半徑,x是過中心垂直于盤面的軸線上場點的坐標.再利用場強與電勢的關系推導電場強度

也有教材和習題解答直接利用場強疊加原理推導上式[1~5].不過,這些公式只適合于x>0的情況.本文利用電勢疊加原理計算軸線上的電勢,再利用場強與電勢的關系重新建立了軸線上的場強公式,用圖形說明了電勢和場強的分布規律.
人們通常將一對半徑相等共軸帶均勻異號電荷的薄圓板當作平行板電容器,這并不正確,因為均勻帶電圓板并不是導體.本文專門研究了均勻帶正負電荷的共軸圓板在軸線上的電場強度,發現軸線上的電場并不均勻,中間是極小值,用圖形直觀地顯示電場的分布規律.文本提出了均勻系數的概念,衡量電場的均勻程度.用圖形說明了均勻系數與兩板之間距離的關系.
2 均勻帶電薄圓板在軸線上產生的電勢和場強
均勻帶電薄圓板如圖1所示,其半徑為R,電荷的面密度為σ(σ>0).

圖1 均勻帶電薄圓板在軸線上產生的電勢和場強
在半徑為ρ處取寬為dρ的一個圓環,其面積為

所帶電荷量為

環電荷到軸線上的場點P的距離為

dq在P點產生的電勢為

其中,k是靜電力恒量.取無窮遠處為電勢零點,利用湊積分法,點P的電勢為
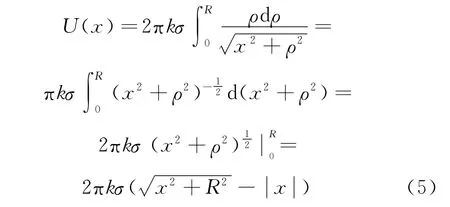
式(5)與式(1)相比,式(5)中出現了絕對值函數.
符號函數定義為


利用絕對值函數的導數的公式,場強為

式(9)與式(2)相比,式(9)中多了絕對值函數和符號函數.筆者曾在文獻[6]中利用絕對值函數表示電勢和場強.在此,對薄圓板軸線上的場強和電勢討論如下:
(1)當R→+∞時,圓板變成無限大平板,在板兩邊產生的場強為


可見:均勻帶電圓形薄板在遠處的電勢和場強接近于點電荷的電勢和場強.
(3)當x=0時,場強為E(0)=0,這是因為圓板內部的場強為零.當x→0+時,sgnx→1,可得圓板正面的場強

當x→0-時,sgnx→-1,可得反面的場強

可見:圓板表面的場強等于無限大均勻帶電平面在空間產生的場強(忽略圓板厚度).
3 場強的無量綱化和可視化
取R為坐標單位,取U0=2πkσR=為電勢單位,則軸線上無量綱的電勢為

點電荷的無量綱電勢為

點電荷的無量綱場強為

利用M ATLAB的函數很容易計算電勢和電場強度,利用作圖指令plot可畫出函數曲線.
如圖2(a)所示,均勻帶電圓形薄板在軸線上的電勢U(x)是偶對稱曲線,在x=0處是一個尖點;當很大時,其電勢接近于點電荷的電勢.如圖2(b)所示,均勻帶電圓形薄板在軸線上的場強E(x)是奇對稱曲線,在x=0處是一個間斷點:E(0+)=E0,E(0-)=-E0,這是薄板兩個表面的場強.由于U(x)在x=0處是一個尖點,其導數并不存在,E(0)=0是補充值,表示薄板內部的場強.當很大時,圓形薄板的場強接近于點電荷的場強.

圖2 均勻帶電圓板在軸線上的電勢和場強
4 均勻等量異號帶電圓板共軸線上的電勢和場強
如圖3所示,兩個圓形薄板共軸,分別帶有面電荷密度為σ的正負電荷,組成一對均勻帶等量異號電荷的薄圓板.設兩板相距為2d(d稱為半距),取x軸為橫軸,則軸線上點P的電勢是兩個圓形薄板電荷產生的電勢之和

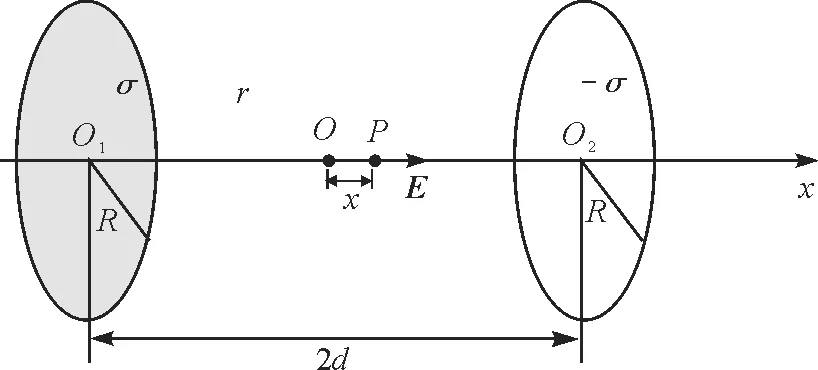
圖3 均勻等量異號帶電圓板共軸線上的場強
點P的電場強度是兩個圓形薄板電荷產生場強的疊加,由于軸線上的場強均沿x軸方向,則總場強

一個均勻帶電圓形薄板的場強E(x)對x的導數為

所以EC(0)在x=0處是駐點.E(x)對x的二階導數為
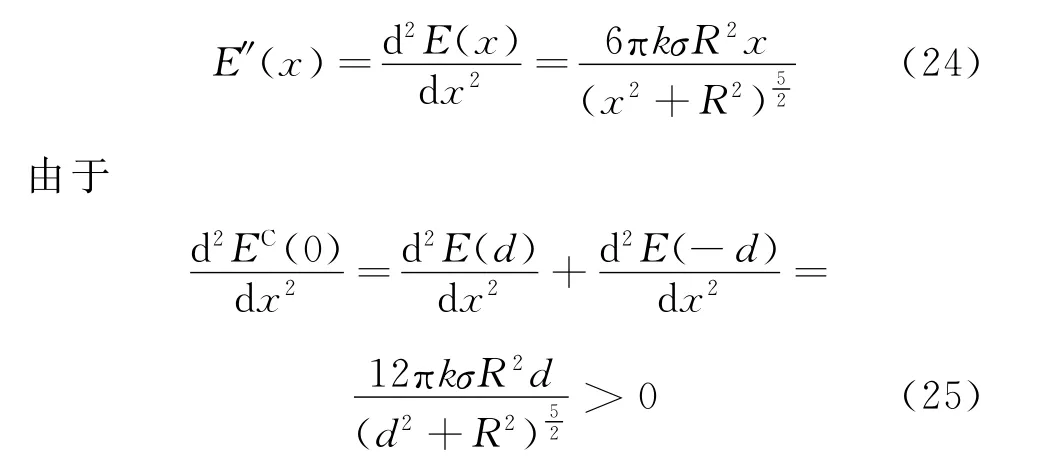
所以EC(x)在x=0處是極小值,說明中心附近的場強并不是均勻的.
在右板的左表面,x=d-,場強為

在左板的右表面,x=-d+,場強為EC(-d+)=EC(d-),即:圓形薄板內表面的場強相等.當d→0時,EC(d-)→4πkσ.
EC(d-)或EC(-d+)與EC(0)之差反映軸線上電場的均勻特性,因此可定義無量綱的均勻系數

將式(21)和式(26)代入上式,可得

均勻系數K取決于半距d.K越大,表示場強越不均勻.
5 均勻等量異號帶電圓板共軸線上場強的可視化
取R為坐標單位,取U0為電勢單位,取E0為場強單位,可以把電勢和場強公式無量綱化,也可以將中心和內邊緣的電場無量綱化.通過圖形可以顯示場強疊加的結果和均勻系數隨距離的變化規律.
如圖4(a)所示,取圓形薄板的半距d=0.2R(大小可以根據需要選取),盡管U+(x)和U-(x)是非奇非偶函數,但是其和UC(x)是奇函數曲線,尖點在x=±d處,兩板之間UC(x)曲線經過原點,幾乎直線下降.如圖4(b)所示,盡管E+(x)和E-(x)是非奇非偶函數,但是其和EC(x)是偶函數曲線,跳躍點在x=±d處;兩板之間的場強EC(x)比較平,在x=0處處微微下凹,是極小值;兩板之外的場強比較小,方向與板內場強的方向相反.當半距d不同時,合電勢UC(x)與合場強EC(x)曲線會發生一些改變,但是大體形狀不變(圖略).

圖4 均勻等量異號帶電圓板共軸線上的電勢和場強
半距d取0.1R到0.25R的值,間隔為0.05R,如圖5(a)所示,不論兩板之間的距離如何,兩板之內的電勢UC(x)都是經過原點的單調下降的曲線,接近于直線;當d不同時,“直線”的斜率稍有不同.如圖5(b)所示,兩板之間的場強EC(x)在x=0是極小值;兩板距離越小,板內的場強EC(x)就越大,也越均勻,板外的場強就越小.當d=0.1R時,板內的場強線又高又平;當d=0.25R時,板內場強線明顯變低且下凹,連中垂線上都不是勻強電場,其他地方就更不是勻強電場了.

圖5 不同距離d的軸線上的電勢和場強
由式(28)可得軸線上場強均勻系數K隨兩板距離d的關系如圖6所示.

圖6 軸線上的場強及場強的均勻系數和分界點
由圖6可知,中心的場強EC(0)和內邊緣的場強EC(d-)或EC(-d+)都隨著半距d的增加而減小,均勻系數K隨著半距d的增加而增加.當K=1%=0.01時,利用M ATLAB可以計算d=0.153 7R.在圖5中,當d=0.1R時,K=0.29%,所以板內場強曲線十分水平;當d=0.2R時,K=2.08%,所以板內場強曲線略顯下凹.可見只有當兩板距離很小時,均勻帶電圓形薄板兩板之間在軸線上的電場才能當作勻強電場,d=0.153 7R是1%均勻性的分界點.
6 結束語
利用M ATLAB可以幫助我們學習和研究電學問題.檢驗公式是否正確的一種簡單方法就是畫出曲線.通過曲線,發現式(1)和式(2)只在x>0的區間才成立.通過慎密演算,就能得到在全部區間都成立的公式.
均勻帶電圓形共軸薄板在軸線上的電場是一個典型問題,比較容易計算,可是,即使在軸線的電場也不是均勻的.電場的均勻性并不是指某一個場強值,而是指電場大小的分布范圍.用均勻系數可以衡量電場的均勻性.均勻帶電的平行薄板在軸線上的場強也可以用同樣的方法研究其軸線上的均勻性.

