Hom-Jordan超代數的構造及超表示的一些結果

黃 楠，楊 宇，陳良云

(東北師范大學 數學與統計學院，長春 130024)

0 引言

20世紀40年代，Pascual Jordan在研究量子力學時，首次提出未命名的Jordan代數，并將其應用于量子力學中[1]。1946年，A.Albert[2]在發表的文章中將它重新命名為Jordan代數，并對一般的Jordan代數進行了更加系統的研究。文獻[2]向我們介紹了Jordan代數的關于右乘算子的基本等式。之后，孟道驥等[3]給我們說明了Jordan代數和結合代數之間存在的某些關系，并介紹了關于Jordan代數結合子的一些性質。更多關于Jordan代數的定義以及性質參見Baklouti等[4]和Baklouti等[5]發表的論文。

Hom-型代數是在原有代數上，將定義代數的等式用一個或幾個線性映射扭曲而成的一類代數，其中這種映射被稱為扭曲映射。當這種扭曲映射是恒等映射時，這個Hom-型代數就變為原來的代數。例如，Harwig和Silvestrov為了更好地描述Witt代數和Virasoro代數，在2006年提出了Hom-李代數的定義[6]，Hom-李代數理論對數學、物理學等的發展起到了十分重要的推動作用。更多關于各類Hom-型代數的內容，可以參考文獻[7-16]。Hom-Jordan代數是Jordan代數的一種形變，近幾年來得到了很多學者的關注。2010年，A.Makhlouf首次在發表的文章中給出了Hom-Jordan代數的定義[12]，他對Hom-Jordan代數進行了介紹并說明了它符合Hom-結合代數的結構，即Hom-Jordan代數可以由Hom-結合代數通過一個加代數誘導出來。2012年，D.Yau對Hom-Jordan代數的一個子類進行了研究[16]，在這種情況下，這類Hom-Jordan代數可以由任意一個Hom-交錯代數產生。近年來，我們在Hom-Jordan代數領域的研究中得出了一些重要性質[10,15]。至于2017年人們才開始研究的Hom-Jordan超代數，是Hom-Jordan代數的一個自然推廣[7]。

本文結構如下。第一部分，給出關于Hom-Jordan超代數的預備知識。第二部分，首先給出構造新的Hom-Jordan超代數的三種方法：用Hom-Jordan超代數的子空間和特征子空間構造它的子代數，兩個Hom-Jordan超代數的直和還是一個Hom-Jordan超代數，Hom-Jordan超代數之間的線性映射是一個態射當且僅當它的圖是一個Hom-子代數。其次得到Hom-Jordan代數的右乘算子和Hom-Jordan超代數的左乘算子的一些重要結果。最后得到了Hom-Jordan超代數的Hom-結合子與Hom-李超代數之間的關系。第三部分，在Hom-Jordan超代數中引入超表示的概念，得到偶的線性映射是超表示的等價條件，并證明左乘映射是超表示。在本文中，總假設所研究的代數是域上特征零的Hom-Jordan超代數。

1 預備知識

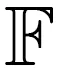
(1)x·y=y·x,

(2)(x2·y)·x=x2·(y·x)，x2=x·x。

定義2[12]183給定一個3元組(V，μ,α)，其中：V是一個線性空間，μ∶V×V是一個可交換的乘法運算，α∶V→V是一個同態。如果對于?x,y∈V，有下面等式成立：

μ(α2(x),μ(y,μ(x,x)))=μ(μ(α(x),y),α(μ(x,x)))，

其中α2=α°α，則稱(V,μ,α)為Hom-Jordan代數。

注1：在定義1中，Hom-Jordan代數還有一個等價定義，見注6。

注2[12]183：因為定義1中Hom-Jordan代數乘法運算是可交換的，所以定義2中的等式也可以寫成

μ(μ(y,μ(x,x)),α2(x))=μ(μ(y,α(x)),α(μ(x,x)))。

注3：當定義2中扭曲映射為一個恒等映射時，我們可以得到Jordan代數的定義。

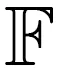
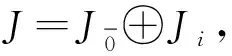
(1)xy=(-1)|x‖y|yx；

(2)(-1)|x‖z|(yx)(zt)+(-1)|x‖y|(yz)(xt)+(-1)|y‖z|(zx)(yt)=(-1)|x‖z|x((yz)t)+

(-1)|x‖y|y((zx)t)+(-1)|y‖z|z((xy)t)。

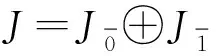
(1)μ(x,y)=(-1)|x‖y|μ(y,x),

(2)(-1)|x‖z|μ(α(μ(x,y)),μ(α(z),t))+(-1)|x‖y|μ(α(μ(y,z)),μ(α(x),t))+

(-1)|y‖z|μ(α(μ(z,x)),μ(α(y),t))=(-1)|x‖z|μ(α2(x),μ(μ(y,z),t))+

(-1)|x‖y|μ(α2(y),μ(μ(z,x),t))+(-1)|y‖z|μ(α2(z),μ(μ(x,y),t)),

則稱(J,μ,α)為Hom-Jordan超代數。

(ii) 稱Hom-Jordan超代數(J,μ,α)是正則的，如果α是一個偶的代數自同構。

(iii) 稱分次子空間W(?J)為Hom-Jordan超代數(J,μ,α)的Hom-子代數，如果α(W)?W且μ(x,y)∈W,對于?x,y∈W。

(iv) 稱分次子空間I(?J)為Hom-Jordan超代數(J,μ,α)的Hom-理想，如果α(I)?I且μ(x,y)∈I,對于?x,y∈I。

注4：在文獻[7]中，作者對Hom-Jordan超代數的一個子類進行了研究，把定義4中的式(2)替換為[7]457：

(-1)|x‖z|μ(α(μ(x,y)),μ(α(z),α(t)))+(-1)|x‖y|μ(α(μ(y,z)),μ(α(x),α(t)))+

(-1)|y‖z|μ(α(μ(z,x)),μ(α(y),α(t)))=(-1)|x‖z|μ(α2(x),μ(μ(y,z),α(t)))+

(-1)|x‖y|μ(α2(y),μ(μ(z,x),α(t)))+(-1)|y‖z|μ(α2(z),μ(μ(x,y),α(t)))。

定義5設(J,μ,α)和(J′,μ′,β)是兩個Hom-Jordan超代數。稱Hom-Jordan超代數間偶的線性映射φ∶J→J′為偶的態射，如果滿足：

(1)φ(μ(x,y))=μ′(φ(x),φ(y)),對于?x,y∈J;

(2)φ°α=β°φ。

定義6[17]Hom-結合超代數是滿足如下條件的一個3元組(V,m,α)，如果對于?x,y,z∈V，有

m(α(x),m(y,z))=m(m(x,y),α(z))，

其中：V是一個超代數，m∶V→V→V是一個偶的雙線性映射，α∶V→V→V是一個偶的同態。

由文獻[3]中環的反同態的定義，我們可以定義Hom-結合超代數的反同態。

定義7設(J,μ,α)和(J′,μ′,β)和是兩個Hom-結合超代數。稱偶的線性映射f∶J→J′為偶的反同態，如果滿足：

(1)f(μ(x,y))=(-1)|x‖y|μ′(f(x)),?x,y∈h(J)

(2)f°α=β°f。

如果f是一個雙射，就稱f是一個偶的反同構。進一步，如果J=J′，就稱f是一個偶的反自同構。

定義8[7]443Hom-李超代數是滿足如下條件的一個3元組(V,[.,.],α)，如果對于?x,y,z∈h(V)，有以下等式成立。

(1) [x,y]=-(-1)|x‖y|[y,x],

(2) (-1)|x‖z|[α(x),(y,z)]+ (-1)|z‖y|[α(z),(x,z)]+ (-1)|y‖x|[α(y),(z,x)]=0,

其中：V是一個超空間，[.,.]∶V×V→V是一個偶的雙線性映射，α∶V→V是一個偶的同態。

注5：當偶同態α為一個恒等映射，(V,[.,.],α)是一個李超代數。

定義9定義一個Hom-Jordan超代數(J,μ,α)的結合子：

設(J,μ,α)是一個Hom-Jordan超代數。對任意非負整數k，用αk表示α的k-次合成。

特別地，α0=id,α1=α。若(J,μ,α)是一個正則的Hom-Jordan超代數，我們用α-k來表示α的逆α-1的k-次合成。

定義10對于任意的非負整數k，我們稱D(∈End(J))為Hom-Jordan超代數(J,μ,α)的αk-導子，如果對于?x∈h(J)，y∈J滿足：

(1)D°α=α°D，

(2)D(μ(x,y))=μ(D(x),αk(y))+(-1)|x‖D|μ(αk(x),D(y))。

對于正則的Hom-Jordan超代數，α-k-導子可用相同方式定義。

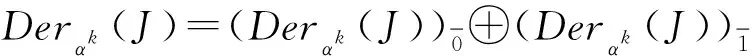
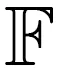
(1)D°α=α°D，

(2)αD(μ(x,y))=bμ(D(x),αk(y))+(-1)|D‖x|cμ(αk(x),D(y))。

對于正則的Hom-Jordan超代數，α-k-(a,b,c)-導子可用相同方式定義。

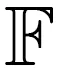
{D∈End(J)|αD(μ(x,y))=bμ(D(x),αk(y))+(-1)|D‖x|cμ(αk(x),D(y)),D°α=α°D}，其中對于?x∈h(J),y∈J。

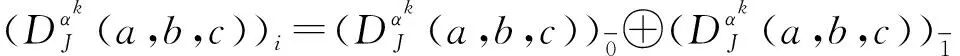
2 Hom-Jordan超代數的構造、左乘算子和Hom-結合子

2.1 Hom-Jordan超代數的構造

性質1設(V,m,α)是一個Hom-結合超代數，那么有下面結論成立。

(1) 定義偶的雙線性映射μ∶V×V→V，

則Hom-超代數(V,μ,α)是一個Hom-Jordan超代數，用V+表示。

(2)定義偶的雙線性映射[.,.]∶V×V→V為

[x,y]=m(x,y)-(-1)|x‖y|m(y,x)),?x,y∈h(V),

則Hom-超代數(V,[.,.],α)是一個Hom-李超代數，用V-表示，

證明(1) 對于?x,y∈h(V)有μ(x,y)=(-1)|x‖y|μ(y,x)。

通過計算，對于?x,y，z,t∈h(V)有

(-1)|x‖z|μ(α(μ(x,y)),μ(α(z),t))=

同理可得，

(-1)|x‖y|μ(α(μ(y,z)),μ(α(x),t))=

(-1)|y‖z|μ(α(μ(z,x)),μ(α(y),t))=

(-1)|x‖z|μ(α2(x),μ(μ(y,z),t))=

(-1)|x‖y|μ(α2(y),μ(μ(z,x),t))=

(-1)|y‖z|μ(α2(z),μ(μ(x,y),t))=

從而

(-1)|x‖z|μ(α(μ(x,y)),μ(α(z),t))+(-1)|x‖y|μ(α(μ(y,z)),μ(α(x),t))+

(-1)|y‖z|μ(α(μ(z,x)),μ(α(y),t))=

(-1)|x‖z|μ(α2(x),μ(μ(y,z),t))+(-1)|x‖y|μ(α2(y),μ(μ(z,x),t))+(-1)|y‖z|μ(α2(z),μ(μ(x,y),t))。

故Hom-超代數(V,μ,α)是一個Hom-Jordan超代數。

(2) 證明方法同(1)。

性質2設(J,μ,α)是一個Hom-Jordan超代數，如下定義End(J)的子空間W：

W={w∈End(J)|wα=αw},

且σ∶W→W,w→αw。如下定義偶的雙線性映射v∶W×W→W,

v(w1,w2)=w1w2+(-1)|w1‖w2|w2w1,?w1,w2∈h(W)，

則(W,v,σ)是一個Hom-Jordan超代數。

證明對于?w1,w2∈h(W)有v(w1,w2)=(-1)|w1‖w2|v(w2,w1)。通過計算得到

(-1)|w1‖w3|v(σ(v(w1,w2)),v(σ(w3),w4))=

(-1)|w1‖w3|α2w1w2w3w4+(-1)|w1‖w4|+|w2‖w3|+|w2‖w4|α2w3w4w1w2+(-1)|w1‖w3|+|w3‖w4|α2w1w2w4w3+

(-1)|w1‖w4|+|w2‖w3|+|w2‖w4|+|w3‖w4|w4α2w3w4w1w2+(-1)|w1‖w2|+|w1‖w3|α2w2w1w3w4+

(-1)|w1‖w4|+|w2‖w3|+|w2‖w4|+|w1‖w2|α2w3w4w2w1+(-1)|w1‖w3|+|w1‖w2|+|w3‖w4|α2w2w1w4w3+

(-1)|w1‖w4|+|w2‖w3|+|w2‖w4|+|w1‖w2|+|w3‖w4|w4α2w3w2w1。

同理可得

(-1)|w1‖w3|v(σ(v(w1,w2)),v(σ(w3),w4))+(-1)|w1‖w2|v(σ(v(w2,w3)),v(σ(w1),w4))+

(-1)|w2‖w3|v(σ(v(w3,w1)),v(σ(w2),w4))=

(-1)|w1‖w3|v(σ2(w1),v(v(w2,w3),w4))+(-1)|w1‖w2|v(σ2(w2),v(v(w3,w1),w4))+

(-1)|w2‖w3|v(σ2(w3),v(v(w1,w2),w4))。

故(W,v,σ)是一個Hom-Jordan超代數。

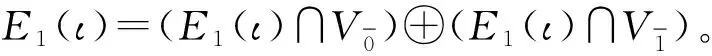
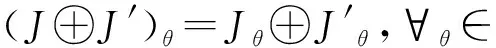
偶的同態(α+β):J⊕J′→J⊕J′定義為

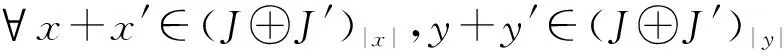
μ″(x+x′,y+y′)=μ(x,y)+μ′(x′,y′)=(-1)|x‖y|μ″(y+y′,x+x′)。

由(J,μ,α)和(J′,μ′,β)是Hom-Jordan超代數，對于?x+x′，y+y′,z+z′,t+t′∈h(J⊕J′)有

|x|=|x′|,|y|=|y′|,|z|=|z′|,|t|=|t′|，

(-1)|x‖z|μ(α(μ(x+y)),μ(α(z),t))+(-1)|x‖y|μ(α(μ(y,z)),μ(α(x),t))+

(-1)|y‖z|μ(α(μ(z,x)),μ(α(y),t))=

(-1)|x′‖z′|μ(α2(x′),μ(μ(y′,z′),t′))+(-1)|x′‖y′|μ(α2(y′),μ(μ(z′,x′),t′))+

(-1)|y′‖z′|μ(α2(z′),μ(μ(x′,y′),t′))。

通過運算得到

(-1)|x‖z|μ″((α+β)(μ″(x+x′,y+y′)),μ″((α+β)(z+z′,t+t′)))+

(-1)|x‖y|μ″((α+β)(μ″(y+y′,z+z′)),μ″((α+β)(x+x′,t+t′)))+

(-1)|y‖z|μ″((α+β)(μ″(z+z′,x+x′)),μ″((α+β)(y+y′,t+t′)))=

(-1)|x‖z|μ″((α+β)2(x+x′),μ″(μ″(y+y′,z+z′,t+t′)))+

(-1)|x‖y|μ″((α+β)2(y+y′),μ″(μ″(z+z′,x+x′,t+t′)))+

(-1)|y‖z|μ″((α+β)2(z+z′),μ″(μ″(x+x′,y+y′,t+t′)))。

故(J⊕J′,μ″,α+β)是一個Hom-Jordan超代數。

性質5設(J,μ,α)和(J′,μ′,β)是兩個Hom-Jordan超代數，且θφ?J⊕J′是偶的線性變換φ∶J→J′的圖。則映射φ是Hom-Jordan超代數間的一個偶的態射當且僅當圖θφ?J⊕J′是性質4中構造的Hom-Jordan超代數(J⊕J′,μ″,α+β)的一個Hom-子代數。

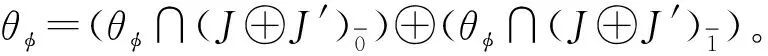
對于?x+φ(x)∈θφ，由于J是一個超空間，故有

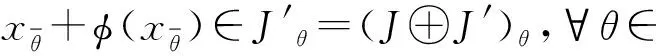
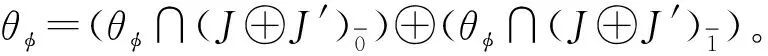
若φ∶J→J′是Hom-Jordan超代數間的一個偶的態射，對?x,y∈J有

μ″(x+φ(x),y+φ(y))=μ(x,y)+μ′(φ(x),φ(y))=μ(x,y)+φ(μ(x,y))∈θφ,

故圖θφ在乘法μ″的運算下是封閉的。此外，由定義5可以得到

(α+β)(x+φ(x))=α(x)+β°φ(x)=α(x)+φ°α(x)，

說明(α+β)(θφ)?θφ。故θφ是Hom-Jordan超代數(J⊕J′,μ″,α+β)的Hom-子代數。

反之，若圖θφ?J⊕J′是Hom-Jordan超代數(J⊕J′,μ″,α+β)的Hom-子代數，有

φ(μ(x+y))=μ′(φ(x),φ(y))。

此外，(α+β)(θφ)?θφ說明

(α+β)(x+φ(x))=α(x)+β°φ(x)∈θφ,

這相當于條件β°φ(x)=φ(x)°α。故φ是Hom-Jordan超代數間的一個態射。

2.2 Hom-Jordan超代數的左乘算子

Hom-Jordan代數的右乘算子Rx與左乘算子Lx是等價的，Rx(y)=Lx(y)，而Hom-Jordan超代數的右乘算子與左乘算子不等價，Rx(y)=(-1)=|x‖y|Lx(y)。所以在這一部分，我們首先介紹Hom-Jordan代數的右乘算子。

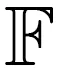
Rx(y)=R(x)(y)=μ(x,y)(?x,y∈V),

為了方便，記R(μ(x,y))=R(xy)。則對于?x,y,z∈V，有以下等式成立：

(1)Rα2(x)Rx2=Rα2(x)Rα(x),

(2)Rα2(x)Rzy+Rα2(y)Rxz+Rα2(z)Rxy=Rα(zy)Rα(x)+Rα(xz)Rα(y)+Rα(xy)Rα(z),

(3)Rx(yz)°α2+Rα2(y)RxRz+Rα2(z)RxRy=Rα(yz)Rx°α+Rxα(z)°α°Ry+Rxα(y)°α°Rz，

(4)R(xy)z°α2+Rα2(y)RzRx+Rα2(x)RzRy=Rα(xy)Rz°α+Rzα(x)°α°Ry+Rzα(y)°α°Rx。

證明Hom-Jordan代數(V，μ,α)中定義的等式為

μ(x,y)=μ(y,x),

μ(α2(x),μ(y,μ(x,x)))=μ(μ(α(x),y),α(μ(x,x))),

可以分別寫成

Rx=Lx,Rα2(x)Rx2=Rα(x2)Rα(x)。

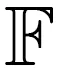
S=R(α2(x+λy))R(x2+2λxy+λ2y2)-R(α(x2+2λxy+λ2y2))R(α(x+λy))=0。

運用R(x)的線性性質可以將上式寫成S=S0+λS1+λ2S2+λ3S3，其中：

S0=R(α2(x))R(x2)-R(α(x2))R(α(x))=0,

S3=R(α2(y))R(y2)-R(α(y2))R(α(y))=0。

故有S1+λS2=0,?λ≠0。

2(Rα2(x)Rxy-Rα(xy)Rα(x))+Rα2(y)Rx2-Rα(x2)Rα(y)=0,

交換上式中的x和y可以得到S2=0。

接下來我們將等式

R(α2(x+λy))R(x2+2λxy+λ2y2)-R(α(x2+2λxy+λ2y2))R(α(x+λy))=0

2[R(α2(x+tz))R(xy+tzy)-R(α(xy+tzy)R(α(x+tz))]+

R(α2(y))R(x2+2txz+t2y2)-R(α(x2++2txz+t2z2)R(α(y))=T0+2tT1+t2T2=0,

T0=2[R(α2(x))R(xy)-R(α(xy))R(α(x))]+[R(α2(y))R(x2)-R(α(x2))R(α(y))]=0,

T2=2[R(α2(z))R(zy)-R(α(zy))R(α(z))]+[R(α2(y))R(z2)-R(α(z2))R(α(y))]=0。

我們可以從以上式子中得到T1=0。然后計算T1就得到定理1中的式(2)，注意到上式暗含著定理1中式(1)。右乘形式的式(2)可以作用于w∈V，故有

μ(μ(w,μ(z,y)),α2(x))+μ(μ(w,μ(x,z)),α2(y))+μ(μ(w,μ(x,y)),α2(z))=

μ(μ(w,α(x)),α(μ(z,y)))+μ(μ(w,α(y)),α(μ(x,z)))+μ(μ(w,α(z)),α(μ(x,y)))。

交換上式中w和x得到

μ(μ(x,μ(z,y)),α2(w))+μ(μ(x,μ(w,z)),α2(y))μ(μ(x,μ(w,y)),α2(z))=

μ(μ(x,α(w)),α(μ(z,y)))+μ(μ(x,α(y)),α(μ(w,z)))+μ(μ(x,α(z)),α(μ(w,y)))。

從而可以得到定理1中的式(3)。在式(3)中，交換x和z可以得到定理1中的式(4)。

至此，我們證明了定理1中4個等式是成立的。

注6：從定理1的等式(2)中，可以得到Hom-Jordan代數的如下等價定義。

給定一個3元組(V,μ,α)，其中：V是一個線性空間，μ∶V×V→V是一個可交換的乘法運算，α∶V→V是一個同態。對于?x,y,z,w∈V，若有下面等式成立：

μ(α2(x),μ(x,μ(y,z)))+μ(α2(y),μ(w,μ(z,x)))+μ(α2(z),μ(w,μ(x,y)))=

μ(μ(α(x),w),α(μ(y,z)))+μ(μ(α(y),w),α(μ(z,x)))+μ(μ(α(z),w),α(μ(x,y)))，

則稱(V,μ,α)是一個Hom-Jordan代數。

接下來，我們研究Hom-Jordan超代數的左乘算子。

定理2設(J,μ,α)是一個Hom-Jordan超代數，令Lx(∈End(J))表示x∈J的左乘算子(即Lx(y)=μ(x,y),?y∈J)。為了方便，記Lμ(x,y)=Lxy。則在Hom-Jordan超代數(J,μ,α)中，對于?x,y,z∈h(J)，有以下等式成立：

(2)Lα(xz)Ly°α+(-1)|y‖z|Lα(x)y°α°Lz+(-1)|x‖y|+|x‖z|Lα(z)y°α°Lx=

L(xz)y°α2+(-1)|y‖z|Lα2(x)LyLz+(-1)|x‖y|+|x‖z|Lα2(z)LyLx,

(3)Lα(xy)Lz°α+(-1)|y‖z|Lα(x)z°α°Ly+(-1)|x‖y|+|x‖z|Lα(y)z°α°Lx=

L(xy)z°α2+(-1)|y‖z|Lα2(x)LzLy+(-1)|x‖y|+|x‖z|Lα2(y)LzLx。

證明由定義4(i)中的式(2)，容易得到所證定理2的第一個結論(1)成立。在定義4(i)的式(2)中，交換y和t得到

(-1)|x‖z|μ(α(μ(x,t)),μ(α(z),y))+(-1)|x‖t|μ(α(μ(t,z)),μ(α(x),y))+

(-1)|t‖z|μ(α(μ(z,x)),μ(α(t),y))=

(-1)|x‖z|μ(α2(x),μ(μ(t,z),y))+(-1)|x‖t|μ(α2(t),μ(μ(z,x),y))+

(-1)|t‖z|μ(α2(z),μ(μ(x,t),y)),

故有

(-1)|x‖z|+(|z|+|y|)(|x|+|t|)Lα(z)y°α°Lx+(-1)|x‖t|+(|x|+|y|)(|z|+|t|)+|z‖t|Lα(x)y°α°Lz+

(-1)|t‖z|+|y‖t|Lα(zx)Ly°α=(-1)|x‖z|+|y|(|z|+|t|)+|z‖t|Lα2(x)LyLz+

(-1)|x‖t|+(|z|+|x|+|y|)|t|L(zx)y°α2+(-1)|t‖z|+|y|(|x|+|t|)Lα2(z)LyLx。

通過計算可以得到所證定理2的第二個結論(2)成立。交換上面等式中的y和z可以得到所證定理2的第三個結論(3)成立。

2.3 Hom-Jordan超代數的Hom-結合子

證明對于?x,y,z∈h(V)有

4μ(μ(x,y),α(z))=m(m(x,y),α(z))+(-1)|z|(|x|+|y|)m(α(z),m(x,y))+

(-1)|x‖y|m(m(y,x),α(z))+(-1)|x‖z|+|y‖z|+|x‖y|m(α(z),m(y,x))。

同理可得

4μ(α(x),μ(y,z))=m(α(x),m(y,z))+(-1)|x|(|y|+|z|)m(m(y,z),α(x))+

(-1)|x‖y|m(α(x),m(z,y))+(-1)|y‖z|+|x‖y|+|x‖z|m(m(z,y),α(x))。

故有

(-1)|x‖y|+|x‖z|m(m(y,z),α(x))-(-1)|y‖z|m(α(x),m(z,y))。

(-1)|x‖y|[α(y),[x,z]]=(-1)|x‖y|m(m(y,x),α(z))+(-1)|x‖z|+|y‖z|m(α(z),m(x,y))-

(-1)|z‖y|m(α(x),m(z,y))-(-1)|x‖z|+|x‖y|m(m(y,z)，α(x))。

最后可以得到

3 Hom-Jordan超代數的超表示

3.1 基本概念

定義12[4]設J1是一個Jordan代數，V是一個線性空間，π∶J1→End(V)是一個線性映射。對于任意x,y∈J1;v,w∈V，定義線性空間J=J1⊕V上的乘法為

(x+v)(y+w)=xy+π(x)w+π(y)v,

如果J是一個Jordan代數，那么我們稱(π,V)為Jordan代數J1在V上的一個表示。

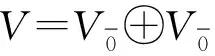
μ′(x,v,y+w)=μ(x,y)+ψ(x)(w)+(-1)|v‖y|ψ(y)(v),

μ′(x+v,y+w)=μ(x,y)+ψ(x)(w)+(-1)|v‖y|ψ(y)(v),

再定義偶的線性映射α+A∶J⊕V→J⊕V為

(α+A)(x+v)=α(x)+A(v),

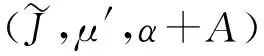
3.2 主要結果

(1)(-1)(|x|+|y|)|z|ψ(μ(α(x),z))°A°ψ(y)+(-1)(|x‖y|ψ(μ(α(y),z))°A°ψ(x)+

(-1)|x‖z|ψ(α(μ(x,y)))ψ(z)°A=(-1)(|x|+|y|)|z|ψ(α(x))ψ(z)ψ(y)+

(-1)|x‖y|ψ(α2(y))ψ(z)ψ(x)+(-1)|x‖z|ψ(μ(μ(x,y),z))°A2,

證明若ψ∶J→End(V)是J在V上的Hom-Jordan超表示，由定義14可知(J⊕V，μ′,α+A)是Hom-Jordan超代數，故有

μ′(x,y)=(-1)|x‖y|μ′(y,x),

(-1)|x‖z|μ′(α(μ′(x,y)),μ′(α(z),t)+(-1)|x‖y|μ′(α(μ′(y,z)),μ′(α(x),t))+

(-1)|y‖z|μ′(α(μ′(z,x)),μ′(α(y),t))=(-1)|x‖z|μ′(α2(x),(μ′(y,z),t))+

(-1)|x‖y|μ′(α2(y),(μ′(z,x),t))+(-1)|y‖z|μ′(α2(z),(μ′(μ′(x,y),t))。

首先，對于所證定理4中ψ滿足第一個等式(1)，若x,y∈J，有μ(x,y)=(-1)|x‖y|μ(y,x)恒成立。若x,y∈V，有0=0恒成立。若x,y有1個在J中，有1個在V中，則有ψ(x)(y)=ψ(x)(y)，恒成立。

其次，對于所證定理4中ψ滿足第二個等式(2)，若x,y,z,t中有2個以上在V中，則乘積為0。若x,y,z,t中有1個在V中，另外3個在J中，則有下面的情況：

第一，若x∈V，則ψ所滿足的第二個等式(2)等價于

(-1)|y|(|x|+|z|)+|t|(|x|+|y|ψ(μ(α(z),t))°A°ψ(y)(x)+(-1)|x|(|y|+|t|))ψ(α(μ(y,z)))ψ(t)°A(x)+

(-1)|x‖y|+|t|(|x|+|z|)ψ(μ(α(y),t))°A°ψ(z)(x)=(-1)|x|(|y|+|t|)ψ(μ(μ(y,z),t))°A2(x)+

(-1)|x‖y|+|t|(|x|+|z|)ψ(α2(y))ψ(t)ψ(z)(x)+(-1)|y|(|x|+|z|)+|t|(|x|+|y|)ψ(α2(z)ψ(t)ψ(y)(x),

(-1)|y‖z|ψ(μ(α(z),t))°A°ψ(y)+(-1)|y‖t|ψ(α(μ(y,z)))ψ(t)°A+

(-1)|t|(|y|+|z|)ψ(μ(α(y),t))°A°ψ(z)=(-1)|y‖t|ψ(μ(μ(y,z),t))°A2+

(-1)|t|(|y|+|z|)ψ(α2(y)))ψ(t)ψ(z)+(-1)|y‖z|ψ(α2(z)ψ(t)ψ(y)。

第二，當y∈V或z∈V時的情況，同理可證，我們也能得到相同的等式。

第三，若t∈V，則所證定理4中ψ所滿足的第二個等式(2)等價于

(-1)|x‖z|ψ(α(μ(x,y)))ψ(α(z))(t)+(-1)|x‖y|ψ(α(μ(y,z)))ψ(α(x))(t)+

(-1)|y‖z|ψ(α(μ(z,x)))ψ(α(y))(t)=(-1)|x‖z|ψ(α2(x))ψ(μ(y,z))(t)+

(-1)|x‖y|ψ(α2(y))ψ(μ(z,x))(t)+(-1)|y‖z|ψ(α2(z))ψ(μ(x,y))(t)，

直接計算得到

故ψ是J在V上的Hom-Jordan超表示當且僅當ψ滿足定理所給條件(1)和(2)。

推論5 設(J,μ,α)是一個Hom-Jordan超代數，則J的左乘映射L∶J→End(J)(滿足：條件L(x)=Lx,?x∈h(J))是J的一個超表示。

證明由定理4可知，L是一個超表示只需驗證下面兩個等式：

(-1)(|x|+|y|)|z|Lα(x)z°α°Ly+(-1)|x‖y|Lα(y)z°α°Lx+(-1)|x‖z|Lα(xy)Lz°α=

(-1)(|x|+|y|)|z|Lα2(x)LzLy+(-1)|x‖y|Lα2(y)LzLx+(-1)|x‖z|L(xy)z°α2，

由定理2中的式(3)和式(1)可得上面兩個等式成立。故L是J的一個超表示。