一類分數階偽拋物方程解的存在性和唯一性
楊階慧,蔣 敏
(貴州民族大學 數據科學與信息工程學院,貴陽 550025 )
0 引言
本研究需要考慮的一類分數階偽拋物方程的初邊值問題為
(1)
其中:ut表示u關于t的偏導數,Ω∈RN(N∈+))是具有光滑邊界?Ω的有界區域,0 分數階拉普拉斯算子最初是在物理學中觀察Levy平穩擴散過程時被提出的,后來也被用于描述等離子體異常擴散、隨機分析和流體動力學等現象[1-2]。分數階微分方程因其在金融學、物理學、流體動力學、種群動力學、最小表面和博弈論等學科研究領域得到廣泛的應用而獲得了重要的地位。分數階微分方程比經典微分方程能更好地描述實際問題。有一些自然現象具有記憶效應,不能用經典偏微分方程來建模,但是可以使用分數階偏微分方程來解決這個問題。因此分數階微分方程引起了廣大數學家和物理學家的關注,也有了重大發展[3-5]。 值得指出的是,Liu等[6]研究了如下具有對數非線性的分數階偽拋線方程 “百善孝為先,難得啊,難得!如此兵亂,你們長官還記得孝悌,就憑這點,見了你們趙長官我就想請他喝一杯。這樣吧,這一帶地形我們熟悉,加上昨天剛從龍游過江,對鬼子布防也比較清楚,我們負責把你們護送到峽口、杜澤、蓮花鎮一線,只要穿越鬼子防線再往西,應該就能看見衢州城。 ut+(-Δ)su+(-Δ)sut=ulog|u|, (2) 依托校企共建生產性實訓基地,開展校企產教融合。結合專業實訓基地條件,與通信企業對接,在真實的工作環境和生產性項目中,實現“教、學、產、研”一體的生產性實訓,進一步提高人才培養的技能水平和職業素養。由企業工程師、專任教師擔任實訓指導教師,將企業工程案例融入課程內容,指導學生分析項目、實施項目、驗收項目等內容,實現學校教學環境和企業真實工作環境的對接。利用基地先進的設備和軟件、優秀的師資團隊通過企業承擔實際工程項目,選拔優秀學生共同參與,讓學生將課堂環境與企業真實工作環境一致,真正做到學校教學內容與工作內容的零距離結合。 在2020年,Ding 和 Zhou[7]研究了如下的基爾霍夫擴散模型 (3) 引理1[11]設X是Banach空間,u∈Lp([0,T];X),ut∈Lp([0,T];X),1≤p≤∞,那么有 受上述工作的啟發,本研究對問題(1)進行了討論,利用Galerkin近似法和壓縮映射原理,得到了該問題解的局部存在性和唯一性。 20世紀70年代日本豐田公司因杜絕生產浪費的系列管理被世界關注,英文單詞LEAN(譯指精實的、去除虛胖的),此前多見于外資企業管理的“精益”,于2013年,在國內首次與醫療行業相結合——這年6月,恩澤集團與美國UL建立合作關系,成為中國“首家精益實踐醫院”,正式開啟恩澤集團的精益醫療之旅。 為了更便捷地陳述結果,下面介紹一些符號、基本定義和引理。 定義L2(Ω)中的內積和范數為 且u(x,0)=u0(x)。 回顧分數階索伯列夫空間的一些必要條件和性質,更多細節可以參見文獻[8-9]。固定s∈(0,1),對任意p∈[1,∞),定義分數階索伯列夫空間Ws,p(RN): 關注p=2時的情況,即Ws,2(RN) ,通常用Hs(RN)來表示。令 X0(Ω)={u∈Hs(RN)|u=0 a.e.在RNΩ內}, 由文獻[10]知X0(Ω)是Banach空間[10],其范數為 具有內積 現將問題(1)的弱解和最大存在時間定義如下。 定義1稱函數u(x,t)是方程(1)的一個弱解,如果對任意T>0,u∈L∞(0,T;X0(Ω)),ut∈L2(0,T;X0(Ω)),?v∈X0(Ω),?t∈[0,T),滿足 (7) 在訴訟中,中國并沒有追究美國商務部是否有權向非市場經濟國家征收反補貼稅,而是直接指出了美國商務部的“非市場經濟方法”造成了雙重救濟從而違反了相關WTO法規。在對反補貼法措施合法性進行分析時,中美雙方爭論的焦點在于中國的國有企業以及商業銀行是否屬于《反補貼協議》中規定的“公共機構”。如果答案是否定的,那么美國商務部反補貼調查中認定的補貼則不應存在,作為結果美國也就不應該向中國征收反補貼稅。 定義2設u(x,t)是方程(1)的一個弱解,定義u(x,t)的最大存在時間Tmax如下: 其中c>0。則由式(14)和式(15)知 綜上所述,本文提出了一種全新的電力運輸方法,就是在雙有源橋拓撲的線路直流潮流控制器。該新方法的提出,在與傳統研究對比時,此類新型電力運輸方式具有無徐額外再次配比電源節能源、有效實現更具靈活性的雙向控制線路直流潮流的優勢。 其中CT(>0)是有界且不依賴于h的常數。因此可得 綜上可知,如今在教育改革以及素質教育逐漸深化以及完善的背景之下實施探究教學,能夠對學生的自主探索、獨立思考這些能力加以培養,可以對教學要求及學生需求進行滿足。數學教師在實施探究教學期間,需要合理設計探究任務,準確把握任務難度及知識寬度,并且合理設置探究情境,積極引導學生探究,不斷增強師生交流互動,一同探究有關問題,這樣才能促使教學效果進行提高。 u∈C([0,T];X)。 本節主要利用Galerkin近似法和壓縮映射原理研究問題(1)的解的局部存在性和唯一性。 定理1對任意T>0,u∈H和u0∈X0(Ω),則存在滿足如下條件的唯一的v使得 v∈C([0,T],X0(Ω))∩C1([0,T],L2(Ω)),vt∈L2([0,T],X0(Ω)) (8) 是如下非線性問題的解 現代文學區別于古典文學的本質特征之一,是知識話語的生產體系不同,無論是文學場域,還是生產主體,都發生了根本性的變革。現代教育在中國的落地生根,是詞學研究學院化和學科化的體制基礎。陳水云認為“直到1917年春蔡元培出任北京大學校長,在國文學門首設‘詞曲’課程,并聘請吳梅、劉毓盤這樣的詞曲專家出任教授,中國詞學現代化局面才算是打開了”⑩,詞學作為一門專業的學科正式進入現代教育的體制中。《詞學季刊》創刊號簡要列舉了20世紀30年代在高等學校任教的詞學教授,如中央大學的吳梅、汪東、王易,中山大學的陳洵等,均在大學講堂傳道授業,培養了大批詞學研究學者,推動了現代詞學的學院化進程。 (9) 證明利用Galerkin方法。設Wh=Span{ω1,…,ωh},h≥1,{ωj}(j=1,2,…,h)是X0(Ω)中的一組基函數,‖ωj‖X0(Ω)=1,‖ωj‖2=1,{ωj}在L2(Ω)和X0(Ω)中是正交且完備的,{λj}表示相關的特征值,令 (11) 是如下問題的近似解 (12) 其中:η∈Wh,t>0。對于j=1,…,h,在式(12)中取η=ωj,可得 (13) (2)融資方式單一。根據調查結果發現,大學生創業選擇融資方式時最先考慮的是融資成功率。由于大學生缺乏社會經驗及較低的信用條件的現狀,銀行貸款“惜貸”使其門檻高而難,獲得天使投資機會的概率又小,因此中國大學生創業者中大部分只能通過親情融資、合伙融資的方式籌集創業基金。因此,為了提高大學生創業成功的概率,激發大學生創新創業的潛能,大學生應在選擇融資渠道上,更加多元化、創新化。 MRI與CT對淋巴結性質的判斷主要是以大小為主,并且將10mm以下作為評價標準。按照此次研究結果顯示,MRI診斷淋巴結轉移敏感度為38.46%,CT診斷淋巴結轉移敏感度為28%。使用小型超順磁性氧化鐵離子作為對比機,能夠對淋巴結轉移情況進行診斷。該種檢查機制主要是注射超順磁性氧化鐵離子之后,鐵離子會被巨噬細胞吞噬,借助磁化反應能夠降低MRI信號。 由u∈H可知‖u‖X0(Ω)和‖u‖2是有界的,因此只需估計式(14)的右邊,采用H?lder不等式和Young不等式有 通過引入一族勢井及其相應的集合,并結合勢井理論構造了解的存在性與初值u(x,0)之間的關系。然后利用Galerkin近似法和勢井族的性質,推導出了問題(2)在次臨界和臨界情況下解的全局存在性和無限時間的爆破性,并給出了全局解的能量泛函的衰減估計值。 (i)如果u(x,t)在0≤t<∞存在,那么有Tmax=+∞; 對于任意T>0,考慮對空間H=C([0,T,X0(Ω))賦予范數 vh→v在L∞(0,∞;X0(Ω))中弱*收斂。 進一步通過在問題(12)中取極限就得到問題(9)的弱解。 競爭中立制度追求的是自由競爭和公平競爭的目標,具體的實施模式在國有企業和私營企業之間通過一系列中立的政策建構競爭環境。而競爭中立最主要針對的對象其實是國有企業。而我國國企的強勢地位是建構競爭中立制度的一大難題,雖然我國在確立市場經濟體制之初就明確了國有企業要建立現代化治理制度,但我國國企特別是如石油、天然氣、電信等公用企業產生的優勢地位已極大影響了市場競爭。我國競爭中立制度若想充分實現其自由競爭和公平競爭的目的,就必須克服國有企業的強勢、優勢地位這一重大障礙。?我國改革國企面臨著極大壓力。改革國企要將其合理地類型化,而非一律進行市場化的轉變,同時還需完善預算和資產管理制度。 如果v和ω是問題(9)的兩個解,那么它們具有相同的初值,通過得到的兩個方程相減可得 整理可得 因此v=ω,故定理得證。 定理2對任意u0∈X0(Ω),T>0,那么問題(1)在[0,T]上存在唯一解。 1.1一般資料2015年5月至2017年5月我院對重癥銀屑病患者48例進行了研究分析,將患肢分成甲乙兩組,均為24例患者。患者最小22歲,最大53歲,(38.11±2.21)歲,共有27例男性,22例女性,兩組普通資料不存在統計學差異性,對結果不產生影響。 由定理1可知,對任意u∈DT,可以定義v=Φ(u)是問題(9)的唯一解。接下來利用壓縮映射原理證明結論u=Φ(u)。 首先,證明Φ是DT到DT的映射,即證Φ(DT)?DT。取u∈DT,那么必存在一個相應的解v=Φ(u),滿足 用類似式(15)的方法估計式(17)可得 大陸村在打造旅游地產之初,就對大陸村的農宅進行整體改造,使之美觀大方,獨具田園特色。大陸村后期整體改造農宅150戶,村民把平頂屋改為坡頂屋,并在屋頂上蓋上小藍瓦,并把墻體粉刷成白色,添加女兒墻、飄檐等,每戶院落的整體設計都不一樣,做到整體風格大致相同,又一戶一景獨具特色。 接下來證明Φ是壓縮映射。取ω1,ω2∈DT,對應地存在v1=Φ(ω1),v2=Φ(ω3),令v=v1-v2,可得 《中華人民共和國印花稅暫行條例施行細則》[9]中明確規定:國家指定的收購部門與村民委員會、農民個人書立的農副產品收購合同免納印花稅。 因此根據壓縮映射原理,得到問題(1)在[0,T]上存在一個唯一的弱解。 分數階拋物方程在科學研究和工程實踐中發揮著重要的作用,許多現象都可以用分數階拋物方程作為數學模型并通過模型、數學方法及相關理論來解決實際問題。分數階導數是一個非局部算子,具有良好的記憶性和遺傳性,而由于一些自然現象具有記憶效應,因此,分數階微分方程比經典微分方程能更好地描述實際問題,使得許多不能用經典偏微分方程來建模的問題,都可以使用分數階偏微分方程來解決。本研究利用Galerkin近似法構造問題的近似解,通過一些常用的不等式手段,得到了本研究所討論的一類分數階拋物方程解的局部存在性定理,再利用壓縮映射原理得到了局部解的唯一性定理。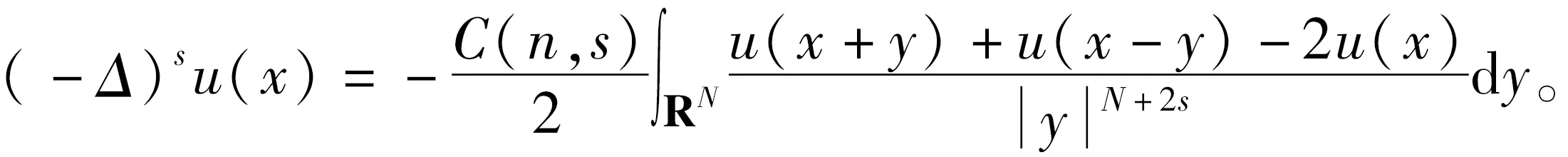
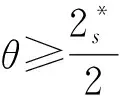
1 預備知識
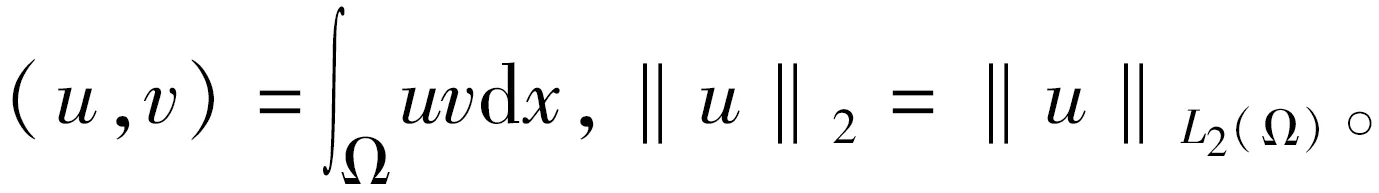
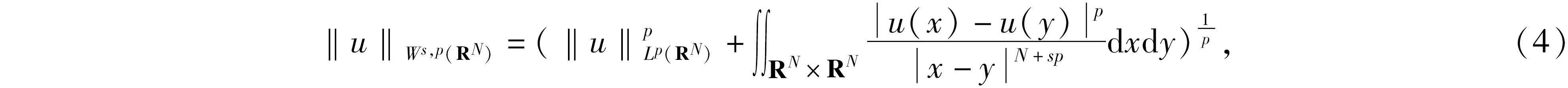
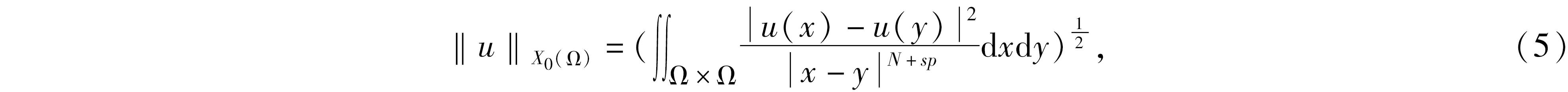
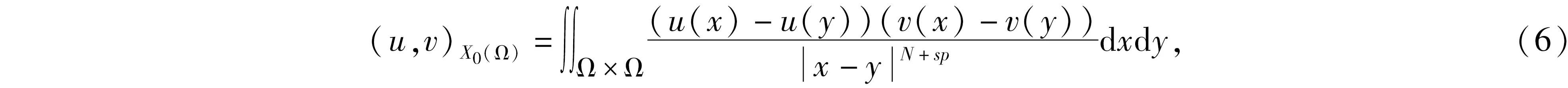
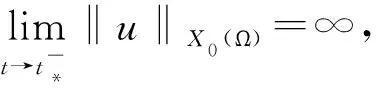
2 主要結果
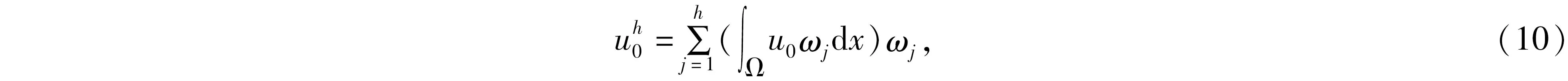

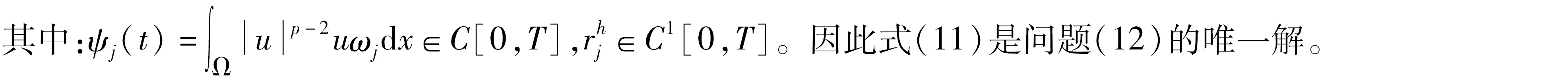
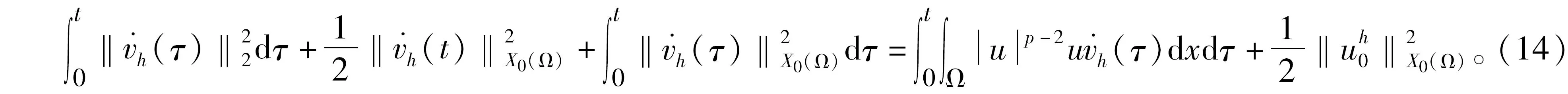
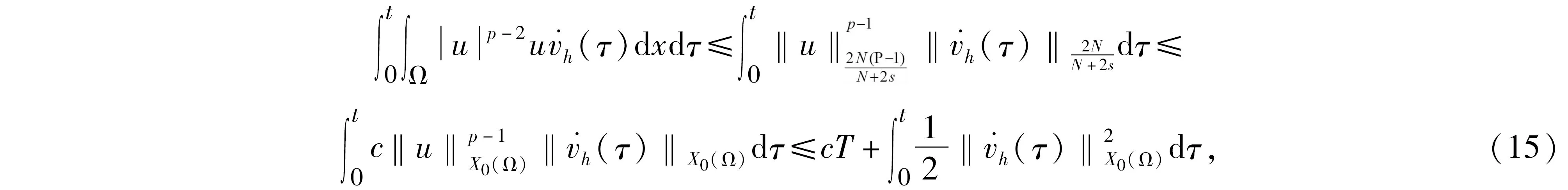
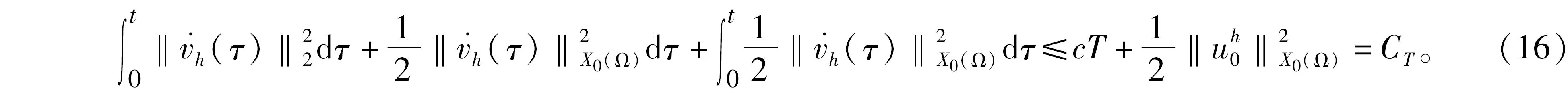


3 結論

