帶屬性偏好的模糊序決策信息系統的分配約簡

徐偉華，李澤峰，黃旭東

(西南大學 人工智能學院，重慶 400715)

0 引言

1982年波蘭數學家Z.Pawlak[1-2]發表經典論文Rough sets，標志著粗糙集理論的誕生。粗糙集已經逐漸成為人工智能中的一個重要分支[3]。近年來粗糙集理論廣泛應用于各個領域，如計算機網絡[4]、圖像處理[5]、數據挖掘[6]和醫學科學[7]等。由于經典的Pawlak粗糙集理論需要嚴格的等價關系，因此只能挖掘具有分類屬性的信息系統中的知識。為了處理其他屬性的信息系統，研究人員將鄰域關系、模糊等價關系、優勢關系和相似關系引入到了Pawlak粗糙集中，建立了鄰域粗糙集[8]、模糊粗糙集[9]、基于優勢關系的粗糙集模型[10]和基于相似關系的粗糙集模型[11]。這些廣義粗糙集模型已廣泛應用于屬性約簡[12-14]、規則提取[15]、決策理論[16-17]、增量學習[18]等。

屬性約簡是粗糙集理論中一個重要的研究范疇[3,19-20]。屬性約簡的原則是在不削弱分類器的分類能力的情況下，刪去不重要的屬性。通過刪去不重要的屬性，可以減少數據的計算量，提高運算效率。目前，很多學者提出了一些新的屬性約簡算法，例如Hu等[21-22]提出的基于鄰域粗糙集模型的屬性約簡算法和基于模糊決策系統可分性的快速魯棒屬性約簡，Chen等[23]提出的區間值決策信息系統下的屬性約簡算法等。

在實際生活中，許多復雜問題都是基于模糊序關系的，甚至是不協調的。信息系統的序關系不同于等價關系的劃分，其結果往往對對象形成的是覆蓋而不是劃分。另外，不協調系統是指基于條件屬性和決策屬性所做出的樣本分類不一致的系統。因此，從這些復雜的信息系統中提取有效的確定性命題，屬性約簡是非常有必要的。在屬性約簡的過程中，人們往往對于部分關鍵屬性有所偏好。為了深入刻畫這一概念，本文在模糊序關系的基礎上，提出了屬性權重向量的概念，并利用屬性權重向量對關鍵屬性值的影響力進行加強，研究了這一復雜信息的分配約簡，所獲結果進一步豐富了粗糙集理論。

1 基于模糊序關系的決策信息系統

決策信息系統是由若干個條件屬性和若干個決策屬性組成的一種特殊的信息系統，其所研究的主要問題即為條件屬性和決策屬性之間的關系。下面將給出一些基本概念。

定義1[19]設I=(U,AT,DT,F,G)是一個5元決策屬性系統；(U,AT,F)為3元信息系統。其中：稱AT為有限條件屬性集AT={a1,a2,…,an}，DT為目標屬性集DT={d1,d2,…,dm}，U是有限對象集U={x1,x2,…,x|U|}，F是U與AT的關系集,F={fk;U→Vk|k≤n}，Vk是ak的有限值域；G是U與DT的關系集，G={gi;U→Vi|i≤m}}；Vi是di的有限值域。

定義2[24]設I={U,AT,DT,F,G}為決策信息系統，如果對任意f∈F,g∈G,a∈AT,以及?d∈DT,x∈U都有

f(x,a)=μa(x)，

g(x,d)∈R(R為實數集)，

其中，μa∶U→[0,1]稱為x∈U在條件屬性a下的隸屬度。則稱滿足上述條件的I為模糊決策信息系統，用I+={U,AT∪DT,F,G}表示。

定義3設WT={w1,…wn}為對應的條件屬性a(∈AT)所對應的權重，其中：對于?wt∈Wt,有wt≥0,并且須滿足w1+w2+…+wn=1。下面給出A(?AT)的得分函數KA(x)的定義為

其中：J=|A|表示集合A中的元素個數，μt=f(x,a),a∈A。

當一個條件屬性越重要時，它所對應的權重值也就越大；反之，它所對應的權重值也就越小。

定義4[19]設I+={U,AT∪DT,F,G}是一個模糊決策信息系統，對于?g∈G,?a∈AT,?d∈DT,?xi,xj∈U，都有

f(xi,a)≥f(xj,a)?Ka(xi)≥Ka(xj)，

g(xi,d)≥g(xj,d)，

則稱該系統為模糊序決策信息系統。

在條件屬性a的值域中可能存在遞增的偏序關系，也可能存在遞減的偏序關系。如果在某一個條件屬性的值域中存在遞增或遞減的偏序關系，則稱此條件屬性為模糊決策信息系統的一個準則。全部的準則構成的集合稱之為準則集。

下文中，只討論由遞增偏序關系構成的優勢關系。

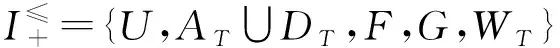
下面在帶有屬性偏好的模糊序決策信息系統中給出的優勢關系為

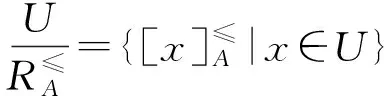
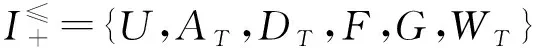
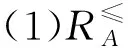
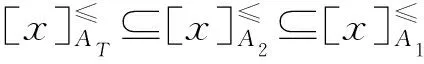
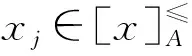
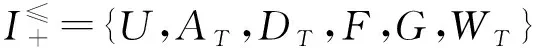
例1表1給出了一個帶有屬性偏好的模糊決策信息系統。U={x1,x2,…,x6},AT={a1,a2,a3},DT=g0gggggg,WT={w1,w2,w3},其中：w1=0.5,w2=0.3,w3=0.2。

根據帶有屬性偏好的模糊優勢關系的定義可以得到：

2 不協調的帶有屬性偏好的模糊序信息系統的分配約簡

下面給出帶有屬性偏好模糊序決策信息系統的分配函數的定義。

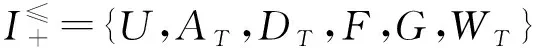
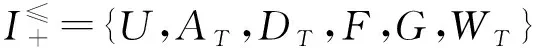
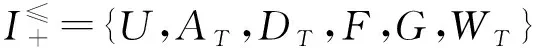
例2根據表1給出的帶有屬性偏好的信息系統計算分配約簡，記：

則有：

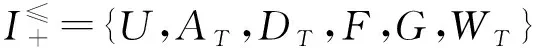
證明必要性：反證法。

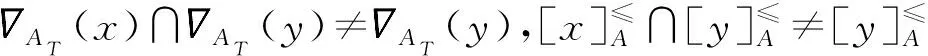
3 不協調的帶有屬性偏好的模糊序信息系統的分配可辨識矩陣

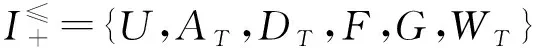
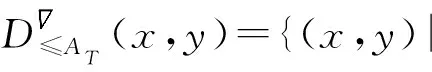
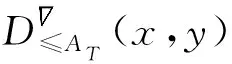
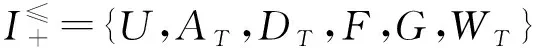
證明必要性：

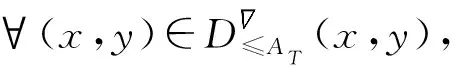
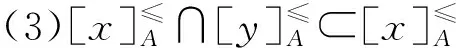
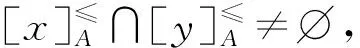
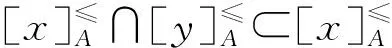
充分性：

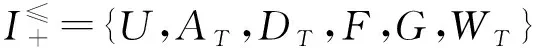
由上面定理3和定義8有下面結論。

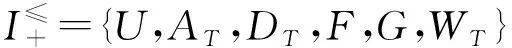
例3對于表1給出的帶有偏好的模糊決策信息系統，接下來計算其分配辨識矩陣(見表2)。

由定理4可得

由以上公式可知該系統的分配約簡與例2中的結果是一致的。

4結論

現實生活中,決策者對系統的每個屬性可能具有不同重視程度。為此，本文在模糊序決策信息系統中結合權重向量的概念，對每個屬性賦予合適的權值，建立了一種新的權重函數。進一步，提出模糊序決策信息系統的分配約簡，并給出其判定定理和求解方法。最后，通過實例驗證了該方法的有效性。然而在具體的應用中，主要的分配約簡方法還是依靠專家系統的數據和決策者自身經驗給出屬性的重要程度。如何科學的給出屬性的權重向量將是下一步研究的主要課題。