雙機器人協同控制研究綜述①

陳 陽,鄭甲紅,王 婧

(陜西科技大學 機電工程學院,西安 710021)

20世紀,隨著機器人技術的飛速發展和日漸成熟,機器人被廣泛應用在各領域中,為工業生產需求提供了很多便利.由于工業生產愈加復雜的工況要求,單機器人已經很難滿足作業要求,眾多科研工作者對雙、多機器人系統展開了深入研究[1–3].同時需要注意的是雙機器人與雙臂機器人并不相同,雖然兩者同樣是使用兩機械臂協同作業,但雙臂機器人只需一套控制系統和一套坐標系,而雙機器人需要兩套控制系統和兩套坐標系.本文針對的是雙機器人協同控制.與單機器人作業相比,雙機器人作業可被用于很多工況復雜環境場合,具有更大的靈活性和負載能力[4–7],也具有更高的可靠性.然而,雙機器人協同作業在具有更多優點的同時,也在研究過程中面臨更復雜的問題.本文針對雙機器人系統涉及的動力學模型建立、軌跡規劃問題[8,9]以及雙機器人作業中的協同控制問題等3 方面研究工作的內容,分析雙機器人系統目前存在的技術漏洞和技術難點,指出未來發展的方向.

1 雙機器人協調系統分類

1.1 機器人特性分類

按照機器人運動特性來分類,機器人可分為以下3 類.

(1)底座固定機器人.此類機器人最大的特點是基座常用鉚釘等物理約束固定在地面上,例如文獻[10–12]提到的機器人.即機器人的基坐標位置固定,且在整個作業過程中都不會發生變化,因此使用此機器人避免了各機器人基座坐標系的坐標轉換,更易獲得各機器人的相對位置.

(2)移動機器人.與基座固定機器人相比,移動機器人的工作場所更廣闊,但同時移動機器人的動力學特性和各機器人之間的坐標關系也更復雜,如文獻[13–15]均對此作了詳細分析和論述.然而由于雙機器人協調系統的應用場合限制,所以常采用固定機器人,本文以基座固定機器人為論述重點.

(3)空間機器人.空間機器人是在空間環境中活動的,代替人類完成工作的機器人.空間機器人可以分為遙操作機器人、自主機器人兩種.例如,空間機器人可以用于代替人類在高空中完成一些地面機器人無法滿足的工作.而空間環境和地面環境差別很大,空間機器人工作在微重力環境中,空間機器人與地面機器人的要求也必然不相同,有它自身的特點.

1.2 雙機器人作業應用分類

與單機器人作業相比,雙機器人作業可被用于更為復雜的應用場合,常用的雙機器人協作被用到軸孔裝配、復雜路徑焊接、搬運大型物體或重型物體等場合,具有更大的靈活性[16]和負載能力[17],也具有更高的魯棒性[18].

(1)軸孔裝配[19–21].在人力勞動密集的裝配中,可采用雙機器人代替雙手進行統一簡單的裝配.例如使用雙機器人進行螺栓螺母裝配,一個機器人精準定位到軸孔位置,將螺栓安裝在對應位置,另一機器人根據螺栓位置,持有螺母,到達相應位置,兩機器人相互配合擰緊螺母,完成裝配.這類應用需要機器人具有極高的定位能力和極強的柔順性,才能完成螺栓螺母裝配的取、放、擰緊這一系列需求,如圖1所示.

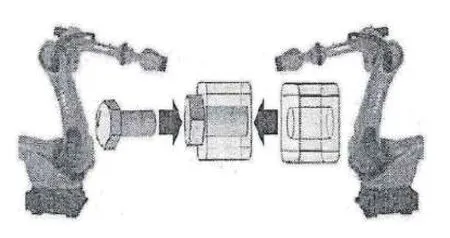
圖1 雙機器人軸孔裝配

(2)復雜路徑焊接[22–24].使用雙機器人進行較為復雜需求的路徑焊接,即一個機器人搬運抬起被操作物體,根據復雜焊縫的最佳起始焊點規劃此機器人運動位置及位姿,另一機器人為焊接機器人,對復雜焊縫進行焊接,如圖2所示.

圖2 雙機器人復雜路徑焊接

(3)搬運物體[25–27].采用雙機器人協作搬運的物體,一般多是尺寸較大或質量較大的物體.根據作業任務需求雙機器人共同完成對被操作對象的抬起、運動、放下等.較為常見的雙機器人搬運,是在雙機器人將需求抬起被操作物體到相應位置后,由其他的焊接機器人對其進行焊接,如圖3所示.

圖3 雙機器人搬運物體

1.3 雙機器人應用耦合分類

雙機器人協同系統的應用大致可以分為兩類:

(1)緊協調任務[28],例如雙機器人對大型重型物體的搬運過程,各機器人與工件間均無相對運動,且保持位姿和速度的嚴格同步,此類任務中各機器人均與被操作物體直接接觸,且末端執行器有力的產生,則對于此類任務各機器人末端位姿滿足:

其中,x1和x2分別表示兩搬運機器人末端位置矩陣,U為兩搬運機器人間的齊次變換矩陣.

(2)松協調任務[29],例如對搬運機器人所搬運的工件使用焊接機器人焊接等,則對于此類任務各機器人末端位姿滿足:

與式(1)中緊協調關系不同的是,松協調表示焊接機器人和搬運機器人間可能存在著一定的相對位移α (t),α(t)為時變向量.

由于松協調任務中各機器人有獨立的操作對象且不構成統一的閉鏈機構,所以解決緊協調形勢下的雙機器人協調運動控制問題更困難,由于各機器人在消除位置誤差時,末端執行器會產生一些力的作用,一部分力用來調整機器人位置,另一部分力會在機器人與被操作物體之間形成內力.如果誤差較大,則會在閉鏈系統中產生巨大的內力,導致被操作物體或搬運機器人扭曲或損壞.

2 雙機器人協同系統數學模型

要想協調好雙機器人系統作業時的運動必須要建立一個能精確描述包含被操作物體在內的系統整體數學模型.要建立數學模型,首先要對其幾何模型進行分析,得出其運動規律生成其物理模型,通過對物體模型中各參數變量之間的關系,確定系統的狀態方程和輸出方程,得出其動力學特性,即可搭建數學模型.而這個模型既要反映機器人的動力學特性又要包括操作對象的動力學特性.搭建數學模型的過程如圖4所示.

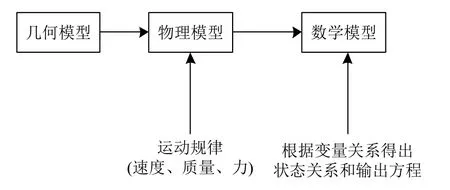
圖4 數學模型搭建過程

2.1 機器人運動學關系與動力學特性

對于雙機器人協同控制,常采用6 自由度垂直型關節機器人.建立單個機器人系統的動力學特性,是建立雙機器人協同系統的基礎.目前的研究對單個機器人的動力學特性,已經取得了較為統一的標識,如文獻[30–34]均采用了如下形式的動力學方程:

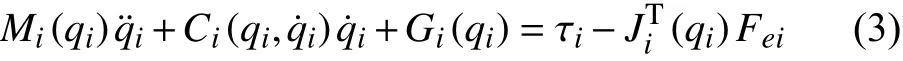
其中,qi,,分別為機器人的關節位置、關節速度和關節加速度;Mi(qi)∈Rn×n為對稱正定慣性矩陣;Ci(qi,q˙i)∈Rn×n為哥氏力與向心力矩陣,Gi(qi)∈Rn為重力作用矩陣;τi為機器人各關節的驅動力矩;Ji(qi)∈Rn×n為雅克比矩陣.雅克比矩陣是反映機器人關節速度到末端執行器運動速度變換關系的矩陣;Fei∈Rn為機器人末端的輸出作用力.對于一般的工業機器人而言,n=6.

考慮一個含有2 個6 自由度機器人機器人協同系統,由式(6)可得出雙機器人數學模型為:

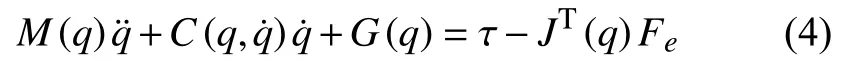
其中,

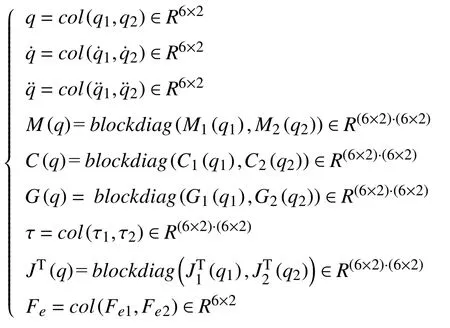
在現實環境中應用時,式(4)的許多參數,如慣性、哥氏力與向心力等大多采用估算的方法,難以獲得精確數據.由于機器人動力學方程是機器人控制的基礎,動力學特性不精確,這就導致機器人在作業過程中有可能出現一些磨損、干擾和噪音,從而影響機器人工作性能或造成一定的破壞.

針對此問題,許多研究者作出了改進,如文獻[35]中,顧新興等基于式(3)的動力學方程引入了一個有界的不確定項di(qi,q˙i,t)∈R6,它表示非精確動力學特性下隨時間所受的干擾.利用滑模誤差得出其相對各參數的補償修正量,使整個系統在一定限制條件下具有較好的魯棒性和動態性能.

另外還有一些研究者通過在控制過程中補償各參數,如文獻[36],Huang 等設計了自適應控制器,用以適應機器人工作空間,可以緩解各參數的不確定性.研究動力學方程是為了更精確的控制機器人,從控制效果來看文獻[36]較傳統方法會更好,也會更精確方便.

2.2 被操作物體動力學特性

目前,大多數雙機器人協同控制只考慮了機器人動力學特性,而忽略了被操作物體的動力學特性.為使雙機器人協同系統動力學模型更加精確,需對被操作物體進行運動學分析,建立他的動力學模型.工業生產中,常用的被操作對象多為剛性物體,其動力學模型類似于機器人動力學模型,例如文獻[37,38].

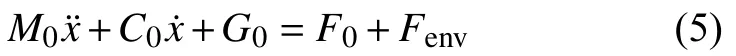
其中,x∈R6為被操作對象的質心在世界坐標系的位姿;M0,C0,G0與式(3)中的對應項含義相同;F0為各機器人在被操作物體上的接觸力矢量,Fenv為環境在被操作物體上的接觸力矢量.

當被操作對象在受到外力無形變發生時,式(5)中的動力學模型成立.但對于一些具有柔性特征的物體[1],例如布料、書籍等,式(5)不滿足其動力學特性,需重新考慮.本文主要針對剛性被操作物體進行分析.

上述式(4)和式(5)分別為機器人動力學模型和被操作物體動力學模型,將兩者結合即是整個協同系統的數學模型.

3 雙機器人軌跡規劃問題

機器人的軌跡,是指操作臂在運動過程中的位移、速度和加速度.軌跡規劃是根據作業任務的要求,計算出預期的運動軌跡.軌跡規劃問題的目的是在無碰撞、無奇點條件下,尋找從起始位置到達目標位置的最優路徑.路徑的優劣取決于規劃算法的優劣.依據算法原理,機器人路徑規劃算法大致分為:傳統算法(如Dijkstra算法、LPA*算法、A*算法等)、智能算法(如粒子群優化算法、遺傳算法等)和其他算法[39].由于軌跡規劃方法具有通用性,即下述單機器人或多機器人軌跡規劃方法同時可用于雙機器人軌跡規劃問題做參考.

3.1 傳統算法

早在1959年,Dijkstra 就提出了Dijkstra (迪杰斯特拉)算法[40].該算法采用貪心模式,其目的是解決單個節點到另一節點最短路徑問題,其主要特點是每次迭代時選擇的下一節點是當前節點最近的子節點,即每一次迭代行進的路徑最短,在每一次迭代過程中,都要對所有節點之前的最短路徑進行更新.近年來,有些學者通過對Dijkstra 算法改進,得出了更優化軌跡.李勁等[41]提出了利用鏈接圖法建立規劃環境模型,該論文將規劃分為兩個層次:用Dijkstra 算法求鏈接圖的最短路徑,得到初始路徑點;用競選算法來調整各個初始路徑點,得到最優的或近似最優的移動路徑點.分析結果表明該方法是有效的.

A*算法是一種啟發式搜索算法,即在搜索過程中建立啟發式搜索規則,來衡量實時位置與目標位置的距離關系,使搜索方向優先指向目標位置,從而提高搜索效率.

LPA* (life planning A*)算法[42]是Koening 等在2004年提出的.該算法是基于A*算法的增量啟發式搜索算法.張汝波等[43]針對復雜不確定的作業環境,將基于動態權值LPA*算法與基于威脅的變步長滾動時域預測策略相結合,提出一種規劃修復方法.該方法解決了水下機器人在航行過程中遇到突發威脅時規劃修復的問題.

3.2 智能算法

粒子群優化算法[44]是由Eberhart 博士和Kennedy博士發明,是通過模擬鳥群覓食行為而發展起來的一種基于群體協作的隨機搜索算法.通常認為它是群集智能 (swarm intelligence,SI)的一種.粒子群優化算法由于其簡單容易實現,目前已經被廣泛應用.

段晉軍[45]提出了一種基于面向被操作對象的分層規劃算法,采用粒子群優化算法求解被操作對象被操作對象的參考坐標系在世界坐標系的相對位姿,然后根據實際應用規劃被操作對象的軌跡.根據被操作對象與機器人末端的約束關系,解出各機器人的運動軌跡.最終得到的軌跡滿足焊接機器人船形焊的要求.

與段晉軍文章有共通之處的是,潘建龍等[46]提出了使用遺傳算法尋找焊接工件的最優焊接位置,計算出焊接的運動軌跡,根據焊接工件與機器人的運動關系,計算出機器人的運動軌跡.二者都是通過規劃被操作對象運動軌跡去規劃機器人軌跡.而不同點在于一個采用了粒子群優化算法,另一個采用了遺傳算法,兩相對比,遺傳算法中以前的知識隨種群而變化,而粒子群優化算法保存所有好的解的粒子,沒有交叉和變異工作,因此粒子群優化算法原理更加簡單,參數更少,更易于實現.

Nazarahari 等[47]基于傳統遺傳算法的基礎上,提出了采用5 個定值的交叉和變異碰撞算子來改進遺傳算法,從而改進路徑.

人工勢場法是路徑規劃常用方法之一,是由Khatib提出的一種虛擬力法[48].它的基本思想是將環境視為一個人造引力場,機器人的運動視為引力場中的運動,定義目標點對機器人有引力作用,障礙物對機器人有排斥力[49],最后通過兩者力結合來控制機器人的運動.因為人工勢場法規劃軌跡同時保證了避障問題,所以大多軌跡都比較平滑安全,但此方法存在局部最小問題(“死鎖”).為克服這一缺點,許多研究者通過將人工勢場法與其他算法結合來改善這個問題.

王維[50]針對機器人路徑規劃中的勢場法的的局部最小問題,提出了結合行為策略的人工勢場法和勢場法結合的綜合算法,這可以實現優勢互補,同時針對多機器人沖突問題,提出了基于勢函數的防碰撞方法.用以質點模型的智能體對改進算法進行實驗驗證,對比傳統勢場法,驗證其有效性和實用性.

Hassan 等[51]提出基于能量逼近的人工勢場法.由簡化勢函數建立三維勢圖,使用虛擬障礙法處理局部極小值,生成地圖并實現全局離線路徑規劃.

王麗[52]在環境已知的情況下前提下,提出了基于遺傳算法的軌跡規劃方法,利用遺傳性算法精確檢測率了沖突距離,并做了改進.在環境未知的情況下,提出了人工勢場法與多種沖突解決方案.仿真結果表明此方法的有效性.

3.3 其他算法

李尤[53]根據移動多機器人系統的結構和面臨柔性的需求,提出了多機器人的軌跡規劃問題實際可以落腳在任務合理分配問題和防碰撞算法設計問題.在任務分配問題中,對比傳統單屬性指派規則,采用了多屬性指派規則,通過使用FCFS、M-FCFS、NAF、M-NAF、DWD、MDWD-R 算法進行實驗對比,得出MDWD-R算法的綜合性能最好,且在運行過程中穩定性好,有較強的魯棒性.在防碰撞算法設計問題中,設計了基于資源申請和釋放的防撞算法,對不同情況下算法對應的局限性提出了等待先行的優化策略、針對地圖設計的優化策略,針對死鎖的優化策略.將優化策略與基于資源申請和釋放的防撞算法結合,就有了改進后的防撞算法,并通過實驗驗證了其可靠性.

歐陽帆[54]為解決雙機器人防碰撞問題,先提出了一種基于八叉樹結構的層級式碰撞檢測球體模型,用于檢測雙機器人的碰撞距離計算和碰撞狀態判斷問題.再提出了使用SAT-SDPD 算法更精確的計算兩機器人末端之間發生碰撞和分離的時間,最短分離距離等.最后提出了一種改進型速度排斥場模型,相較于常用的人工勢場法不需要力矩驅動,但此方法在避障軌跡規劃中容易出現穿透和陷入局部最小問題.

4 雙機器人協同控制系統模型

目前針對雙機器人位置/力協調控制的模式大致可以分為4 種,主從控制、位置/混合控制、阻抗控制、同步控制.下面對這4 種控制方式一一介紹.

4.1 主從控制

主從控制可以分為兩類,一類是leader-follower 主從控制,另一類是master-slaver 主從控制.如圖5所示.leader-follower 主從控制是采用純位置控制.而masterslaver 主從控制其控制思路是定義master 機器人為主機器人,slaver為從機器人,主從之間滿足一定的約束關系.Master 機器人采用基于位置的控制方式,slaver機器人采用力反饋的控制方式,從機器人通過六維力/力矩傳感器簡介獲知主機器人的運動趨勢實現對主機器人的跟隨運動.由于leader-follower 主從控制方法忽略了對機器人間力控制問題的研究,容易造成機器人損壞,或接觸工件破壞.因而常用master-slaver 主從控制對雙機器人進行協同控制,如文獻[55]采用masterslaver 主從協調策略來實現對物體的搬運,并提出力控制在協調過程中的重要性.但是這種控制方式需要從機器人具有較強柔性,能夠快速地做出響應,否則可能會導致系統不穩定.

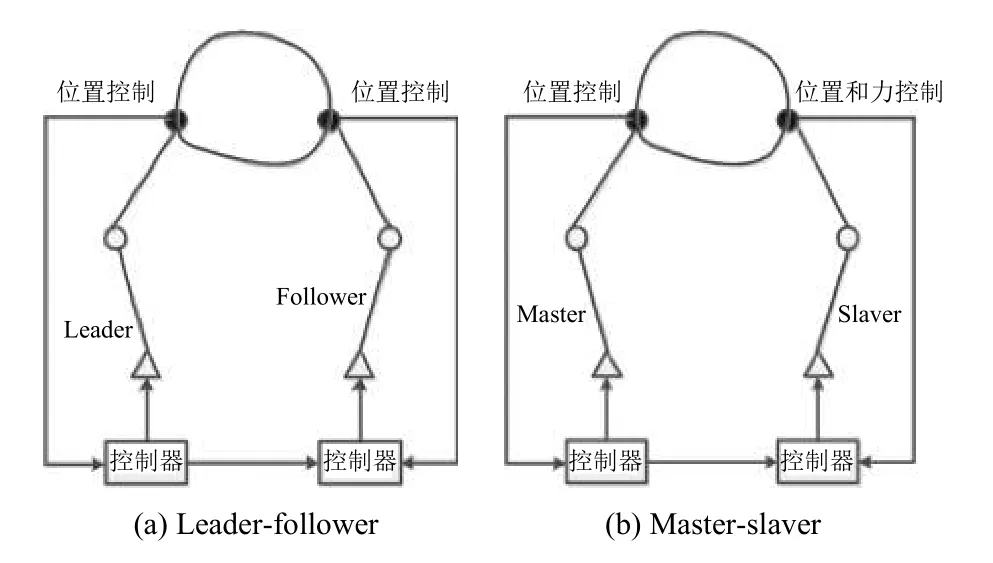
圖5 主從控制方式

4.2 位置/力混合控制

位置/力混合控制,其控制思想是雙機器人控制角色相同,沒有主從之分.在雙機器人位置/力混合控制中,將各機器人末端的運動進行分解,通過選擇矩陣來實現空間的劃分,在自由空間采用位置控制,可以實現對期望位置的跟蹤.在約束空間采用力控制,可以實現對期望力的跟蹤[56–58],對接觸力與期望值的偏差進行補償.如圖6為位置/力混合控制原理圖,在位置/力混合控制結構中,系統是位置、力控制的雙輸入雙輸出,通過選擇矩陣S來決定控制方式,S為6×6的對角矩陣,矩陣元素只能為0 或1,I是6×6的單位矩陣,I–S則為力子空間選擇矩陣,輸入Xd為期望位置,Fd為期望力,輸出q為機械臂旋轉角度,h為實際接觸力.雖然該控制模式既有位置跟蹤又有力的控制,但該控制模也有其缺點.如文獻[56,57]采用位置/力混合控制,導致在自由空間向約束空間過渡不能保證系統的柔順性.另外該控制方式適用于力矩接口控制的機器人,而大部分商用的工業機器人并沒有提供力矩接口,因此使用該控制系統有很大的局限性.

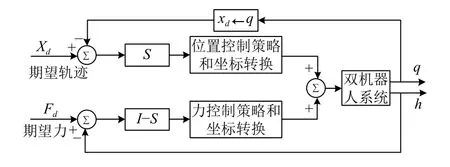
圖6 位置/力混合控制結構圖

4.3 阻抗控制

1985年,Hogan 提出了阻抗控制[59],它是由剛度控制和阻尼控制相結合的一種控制方法.在實際應用中,導納特性與阻抗特性是不可分割的.導納控制是輸入力輸出位置,阻抗控制是輸入位置輸出力.其轉換關系如圖7.其中,z表示阻抗大小,1/H表示導納大小,Xd為期望位置,X表示實際位置,?X表示期望位置與實際位置之間的位置誤差,Fext表示機器人末端與環境的接觸力.

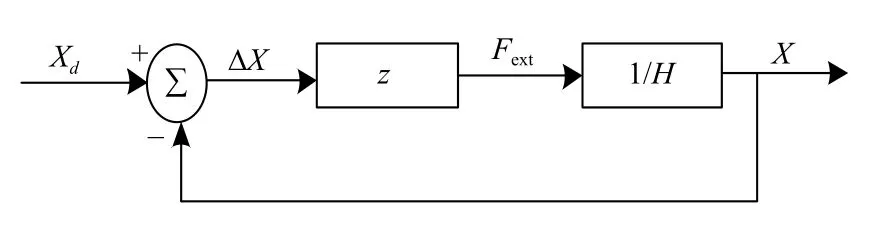
圖7 阻抗控制和導納控制的關系圖

由于其簡單易實現的優越性,許多學者對此進行了深入研究,擴展出了多種更優化方法.按控制量的不同,阻抗控制可以分為基于力矩的阻抗控制方法和基于位置的阻抗控制方法.

基于力矩的阻抗控制方法,是建立關節空間和笛卡爾空間的力/位置轉換關系:

根據式(4)的機器人動力學模型,采用如下的控制律:

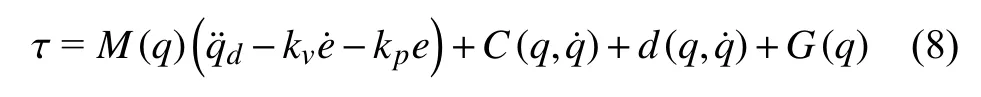
其中,e表示關節位置誤差(e=q?qd),kp表示比例系數,kv表示微分系數,J(q)為雅克比矩陣.基于力矩的阻抗控制需要有一個完整且精確的動力學模型才能實現,而環境參數大多未知,且難以精確獲得,因此在實際控制中很少使用此種方法.

基于位置的阻抗控制實際上是一種間接力控制方法,是以阻抗模型為基礎,通過調整機器人位置誤差間接調整機器人末端力,實現力控制,其控制原理如圖8所示.

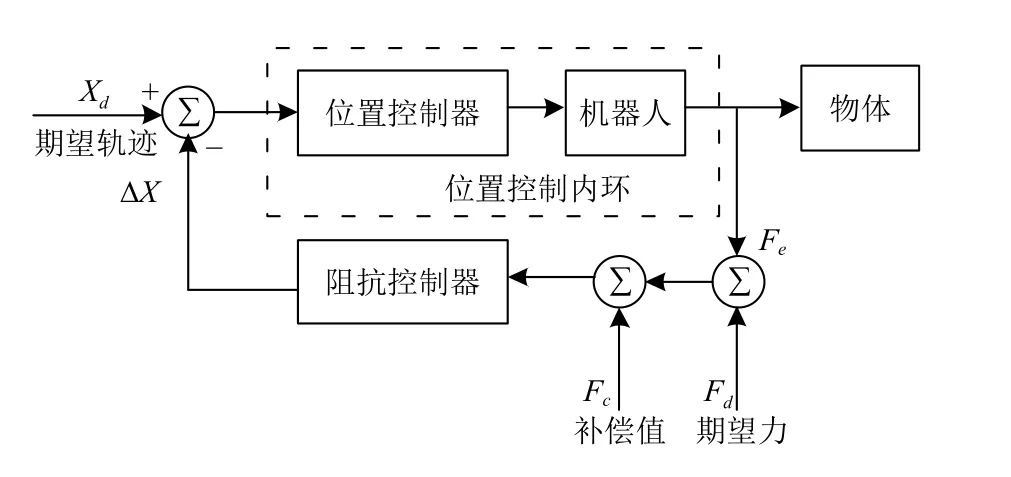
圖8 基于位置的阻抗控制結構圖

由于基于力矩的阻抗控制方法依賴于精確的機器人動力學模型,相比而言,基于位置的阻抗控制方法的使用更廣泛,也更易于實現.

4.4 同步控制

同步控制,是一種基于模型的控制方法,主要針對期望軌跡跟蹤.如文獻[60]在使用同步運動的模式的基礎上,采用自適應的控制策略,對每個單機器人做軌跡跟蹤控制,使兩機器人在同一時刻的位置誤差為0.然而同步控制模式主要做機器人的軌跡跟蹤,對力控制問題有所忽視,因此此控制模式很少被應用.

4.5 雙機器人協同控制方法

常用的雙機器人協同控制方法有PID 控制,模糊控制,遺傳算法,強化學習等.在工業生產應用中,與單機器人控制相比,雙機器人協同控制較為復雜,需要處理各機器人之間的約束關系和內力分配等問題.而單一控制模式和控制方法很難實現對其控制.因此,雙機器人協同控制多是采用多種控制模式與多種控制方法的控制律相結合的方式完成作業任務.

如Bonitz 等 [61]提出了面向被操作對象的協調策略,并對作用于物體的合力進行力分解.Caccavale 等[62]在文獻[49]基礎上提出了面向被操作對象的內外阻抗控制策略.

歐陽帆[54]針對雙機器人搬運作業中的內力控制問題,提出基于遺傳算法的阻尼比例微分控制方法.仿真結果顯示使用遺傳算法優化PD 參數后的控制效果相比純剛度控制最優的控制效果要更好一些.

周揚[63]提出面向物體的多空間阻抗控制策略,實現物體阻抗和機器人阻抗融合,為避免機器人對物體的作用力和物體對環境的作用力過大,提出自適應阻抗控制方法.機器人自適應地調整了物體的阻抗參數,補償了環境不確定性,提高了控制精確度.賀軍[64]提出了變負載的雙臂協作機器人雙環自適應阻抗控制方面的研究,設計了基于模型的非線性控制系統.雖然上述研究考慮了雙臂對物體的內力和外力控制,但是大多都采用定阻抗的控制策略,并沒有考慮存在外部干擾和內力約束下的影響.

田獻軍[65]提出了基于模糊控制原理與BP 神經網絡結合的軌跡跟蹤控制方法,模糊控制不依賴于精確地數學模型,能夠克服操作對象不確定性的影響,但模糊規則的建立和更改都比較有難度,而BP 神經網絡的自學習能力可以模擬模糊推理,并且在實際應用中可以不斷進行修正.實驗結果也驗證了,雖然剛開始會有一定的超調,但相應速度很快,實際位置會迅速逼近期望位置.

丁楠[66]針對多機械臂抓取被操作物體,提出了一種基于滑模補償的力/位混合控制方式,后因滑膜控制常有的抖震問題,提出了基于模糊增益自適應調整的滑模控制,使控制過程更加穩定,達到了更好的控制效果.

潘建龍等[46]提出了在雙機器人搬運工件時采用主從控制模式,主機器人采用位置控制,從機器人采用基于自適應阻抗控制的方法,實現從機器人末端位置誤差與力之間的關系的轉換,進行位置和力的控制.

段晉軍[45]提出了對稱式自適應變阻抗的位置力控制算法,視雙機器人與被操作對象為一個閉鏈系統,根據其約束關系,將機器人末端劉維力矩傳感器測得力,分解為外力和內力.外力用來平衡被操作物體動力學以及環境施加在物體上的接觸力,即外力是用來進行軌跡跟蹤的.內力不會產生任何的運動,用來表述機器人與物體之間的內力,即內力是用來進行力跟蹤,保證內力不會對機器人與被操作物體造成損傷和破壞.在內外力進行分配的同時,設定雙機器人在x、y軸使用位置控制,在z軸使用力控制,即對雙機器人使用混合力位控制的同時,使用力分解阻抗控制.通過實驗驗證,機器人在無干擾情況下可以按照期望軌跡運動,在有干擾時,會有一定誤差,干擾消失后,可以迅速調整回到期望軌跡,表明了其控制極大的柔順性.

蘇越[67]在雙機器人協同中,提出了主從式雙臂力位混合控制的控制方法,主機器人采用基于位置的阻抗控制,從機器人采用力位混合控制.最后搭建了實驗平臺,對雙機器人搬運和雙機器人擰瓶蓋分別進行了實驗,驗證結果表明該控制方法的有效性.

Perrusquia 等[68]提出了基于強化學習的阻抗控制方法,利用阻抗控制生成機器人搬運作業中的期望力,在使用強化學習得出最優期望力,進行位置力控制.實驗結果表明Q(λ)算法的學習迭代次數更少,且位置力跟蹤效果最好.

除上述之外,還有一些智能控制策略[69,70]也被用到了協同控制中.這種控制方式依賴于動力學模型,由于存在動力學建模難、控制過程過于復雜、強耦合、非線性等難題,還未應用在現有的控制系統中.

5 研究展望

目前,雙機器人協同控制的研究才剛興起,在動力學分析和控制分析等方面還存在很多問題.通過以上雙機器人協同控制的研究綜述可以看出,目前的控制方法雖能實現一些簡單的作業需求,但仍存在精度不夠或協同性能差的問題.為使雙機器人協同能更好的實現更復雜任務,本文認為以下問題值得更深入研究.

(1)被操作物體動力學特性統一化.被操作物體是整個系統很主要的一部分,數學模型是實現控制的基礎,建立具有普遍性、合理性的被操作物體動力學模型至關重要.

(2)雙機器人與被操作物體之間的約束關系分析.與單機器人相比,雙機器人協同系統最大的難點在于各個之間的運動約束關系,然而這在目前的研究中都有所忽略,或太過簡化.這就導致現在的協同無法實現在時間上同步,在空間上約束.因此,雙機器人與被操作物體的約束關系將是以后的研究重點和研究基礎.

(3)控制方法的性能評價.目前的控制方法多種多樣,許多研究者將各種方法結合對機器人進行控制,雖然通過仿真結果可看出均可實現軌跡跟蹤,但控制策略的正確性與合理性缺少評價標準.控制方法的性能評價,對控制策略提供了評價準則,為實際應用提供了保障,具有重要意義.

(4)智能控制的應用.智能控制是未來機器人控制的一個大趨勢.由于雙機器人作業環境的易變性和不可預見性,為實現機器人智能決策能力,應從傳統的機器學習,邁向深度學習和強化學習,通過多次學習尋求最優行動.機器人在學習過程,對不好的行動及時報警提示,對優化的行動保存并繼續執行,實現機器人的自適應性和安全保障.

隨著雙機器人協同技術的不斷發展,在未來一定會有更廣闊的市場應用.