基于時空特征區域神經網絡的施工隧道沉降量預測①

林廣東,何 軍,申小軍,徐龍飛,徐衛獎

1(中交一公局集團有限公司,北京 100024)

2(中交隧道工程局有限公司,北京 100102)

3(長安大學 公路學院,西安 710064)

當前,國內隧道建設進程處于高速發展階段,且正由東部轉站中西部.在復雜山區地形下,隧道施工存在高風險、管理難、施工方式落后等諸多問題.通過各類傳感器可以輔助監測隧道的施工及安全狀態,并為管理和施工者提供合理決策.針對實時監測量僅能反映出隧道當前的各項安全指標,對于未來可能出現的潛在風險并沒有前瞻性的不足,國內外諸多學者開展了針對隧道地表下沉量、拱頂下沉量和周邊收斂量等預測研究,并取得了一定的研究成果.總體而言,對于隧道變形預測的方法主要有經驗法、回歸分析法、灰色系統理論模型、人工神經網絡等.對于經驗法,因為存在較大的主觀性,現已采用較少,多為輔助使用,回歸分析法介于只適用于一些靜態數據的處理,因此很難用于隧道沉降這種動態的模型分析,灰色理論法,該法于1982年由鄧聚龍教授提出[1],最早被用于農業和經濟領域,隨著經濟建設的發展,逐步被運用于土木工程領域,并在建筑物的沉降、邊坡的長期變形預測、混凝土長期強度的變化的預測等方面取得一定成果,如胡亮等[2]對高速公路隧道進行灰色理論模型預測,賈承輝等[3]基于激光斷面儀運用灰色理論對隧道進行變形預測,胡達[4]、張錦等[5]基于改進灰色理論模型對隧道圍巖變形進行監測,并取得較好的監測效果.但隨著實際工程應用的增多以及對該理論研究的深入,諸多學者發現,灰色理論對數據的要求較高,要求數據具備指數遞增或單調性,在很大程度上限制了它在具有非線性變形特點的隧道上的應用.

基于數字技術的發展,人們對神經網絡的研究越來越深入,目前,各類人工智能算法已經得到突飛猛進的進步,包括經典的BP 神經網絡以及新型的諸如長短期記憶人工神經網絡(LSTM)等深度學習算法在計算機視覺、語音識別、文本分類等領域都得到了廣泛的應用并取得了良好的效果.在隧道監測領域也有部分應用,例如,廖小輝等[6]基于BP 神經網絡分析預測了混凝土的抗壓強度變化,趙摯南等[7–9]結合數值分析軟件研究了基于BP 神經網絡鄰近地鐵基坑土體參數反演規律的變化,且取得了較好的分析結果.武鐵路[10]以廣州地鐵7 號線為例,采用深度學習方法對破碎帶盾構施工沉降進行預測分析,并分析了預測結果與實測值來驗證預測模型的有效性.曾學宏等[11]將LSTM網絡應用于地鐵隧道的沉降變形分析,并取得了較高的預測精度.孫鈞等[12–15]將人工神經網絡和智能模糊邏輯應用于施工變形預測,且已經在上海沿江通道中得到階段性試驗應用.

然而,相較于回歸分析、支持向量機等經典方法,人工神經網絡在隧道施工安全狀態監測領域應用的研究仍較為欠缺[16–18].目前人工神經網絡在隧道施工安全狀態監測領域應用已經得到驗證,但是目前的研究主要是將人工神經網絡運用在參數明確、機械化程度高的盾構隧道工程中,對爆破等施工因素引起的隧道地表下沉預測研究較少;且現有監測方法多為基于時間序列的指標預測,鮮有文獻將隧道指標的監測特征區域作為人工神經網絡的分析、擬合和預測對象.

鑒于此,本文提出了一種基于特征區域(feature region,FR)神經網絡的隧道地表沉降狀態預測模型.通過采集白家莊隧道欒川端的地表觀測數據對所提方法的預測性能進行算例分析,以此檢驗基于時空特征區域神經網絡的施工隧道沉降量預測方法的準確性和可靠性.

1 基于FR 神經網絡的構建

1.1 建模思想

在隧道領域,基于神經網絡構建的模型越來越多,總結來說主要有對圍巖的變形預測、隧道地表沉降的預測、隧道巖體位移的預測、隧道支護形式的穩定性的評價等,更具體的來說,以往對隧道的變形方面的預測都是基于時間特性的預測,但傳統的基于時間序列的隧道地表沉降量預測方法多數只考慮了時間特性,而在時空特征等方面卻很少有考慮,而實際隧道的變形卻是一個隨時空變化的動態變形過程,這種過程不僅融合了時間特性,更是與周邊環境氣候等多因素相關,因此,為準確預測隧道的沉降量,預測模型的關注量融合了隧道時空特征的監測狀態,而非單一時間序列下的指標.經典預測算法的技術路線和基于FR的技術路線對比圖如圖1所示.

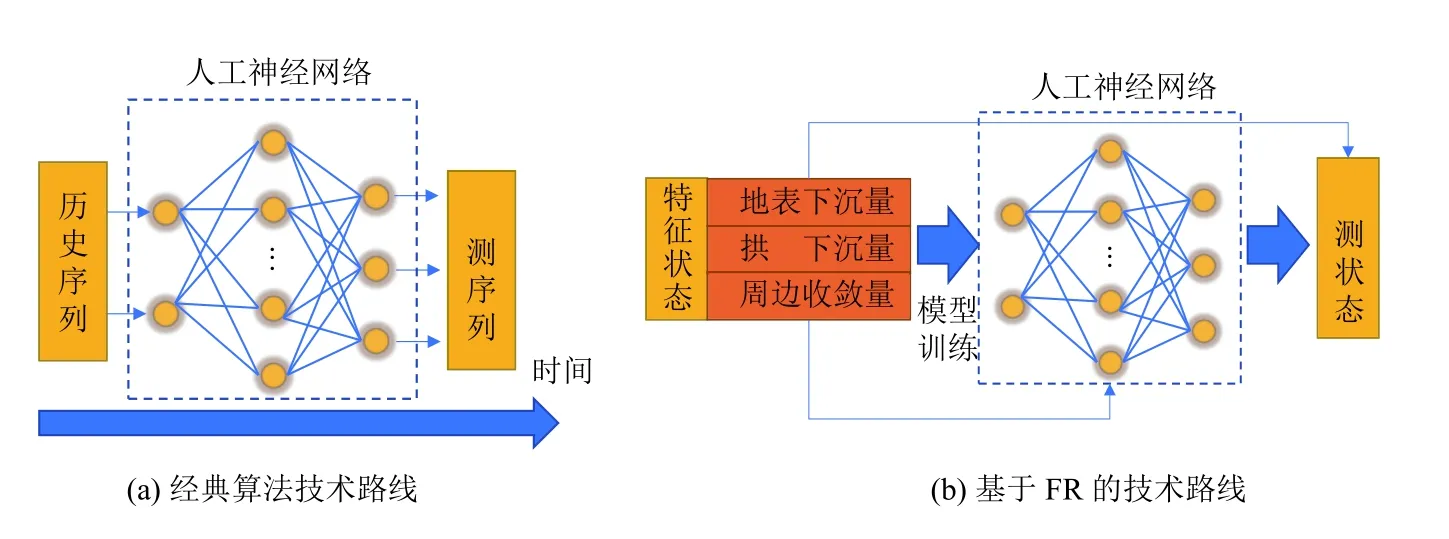
圖1 技術路線對比

基于FR的人工神經網絡隧道特性狀態預測步驟為:首先,基于大量實測隧道監測歷史數據篩選能夠代表隧道施工狀態的特征變量,并借助多源數據融合提取關鍵變量;其次,通過人工神經網絡(BP 神經網絡、LSTM神經網絡)訓練學習諸如地表下沉量、拱頂下沉量和周邊收斂量等隧道特性數據的典型演化趨勢;最后,依據訓練后的神經網絡做出空間特征度量的狀態預測,為隧道監測即施工管理規劃提供合理建議與參考.

需要說明,上述隧道特征量的篩選主要用到K-means聚類方法:首先,隨機選取k個聚類中心,并計算各特征點與聚類中心的多維空間距離;其次,依據計算結果為各特征點分配簇,并計算簇心;隨后,迭代計算特征點群的空間距離,確定相應的簇及簇心,直至滿足終止條件;最后,當各特征點距離簇心的全局誤差平方和滿足設定要求后,終止迭代計算.特征區域可以反映出沉降量、收斂量等的平均演化特征,減小神經網絡的計算復雜度.

1.2 空間特征度量

為衡量個體特征點之間的相關性,常采用如下兩種距離計算方法,即切比雪夫距離和曼哈頓距離.個體特征點在多維空間中的無量綱距離越遠就表明個體差異性越大.

(1)切比雪夫距離(CD)

CD的具體計算公式如式(1)所示:

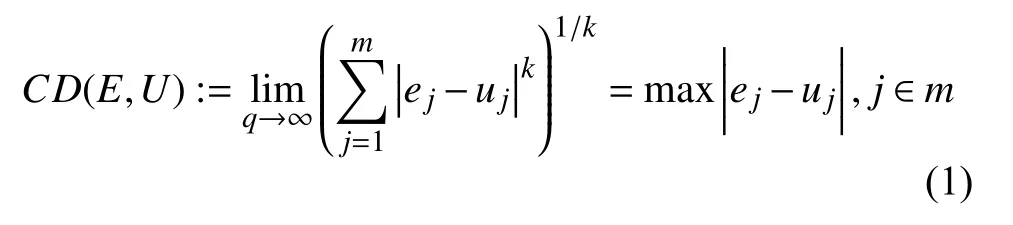
(2)曼哈頓距離(MD)

MD的具體計算公式如式(2)所示:

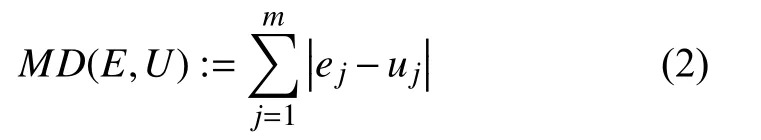
1.3 網絡架構

網絡架構圖如圖2所示,網絡隱藏層選用tansig函數,輸出層選用purelin 函數.對于BP 神經網絡,隱藏層神經網絡的個數選擇如經驗公式(3).

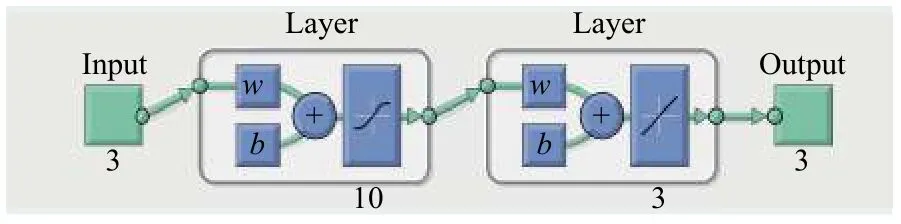
圖2 神經網絡架構圖

其中,L為網絡隱藏層節點數,I為輸入層數,O為輸出層數,δ為經驗選取值,一般取值在1–10 之間.

定義網絡傳播誤差為:

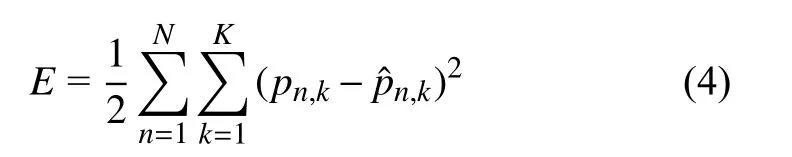
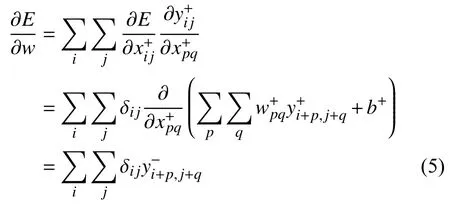
圖2所示神經網絡的輸入為隧道地表下沉量的觀測平均值、相對變化值和累計變化值經聚類后的監測量.隱藏層依據經驗公式(3)選擇神經元個數為10.輸出層的輸出量分別為沉降量的觀測平均值、相對變化值和累計變化值的預測值.

2 工程實例

2.1 數據來源

此工程采用的數據均來源于河南省鄭西高速欒雙段白家莊隧道欒川端的左線和右線地表實時觀測數據,隧道左線樁號ZK104+214–ZK105+526,全長1 312 m;右線樁號K104+116–K105+416,全長1 300 m,為河南省鄭西高速欒雙段在建隧道群中最長隧道,隧道地處于華北陸塊南緣與秦嶺構造帶的結合部位,大部分位于昆侖–秦嶺構造帶東段,在該段巖片北邊界附近常見古生代輝長閃長巖及斜長花崗巖侵入體成帶分布,它們是二郎坪群火山活動晚期的同源巖漿侵入活動產物,Ⅳ、Ⅴ級圍巖居多,且巖體性質較不穩定,在隧道開挖過程中,常伴有圍巖脫落等情況,容易造成超挖等現象,被工程建設稱為“最難啃的骨頭”,因此,隧道采用臺階法開挖,并嚴格遵守短進尺、弱爆破原則.

為防止隧道因爆破等施工因素引起隧道較大的變形沉降,提出了基于特征區域神經網絡的隧道地表沉降狀態預測模型進行案例分析,以準確對隧道開挖過程中可能出現的變形進行準確及時預測.數據采集時段為2019年8月25日–2019年9月14日,每日觀測3 次,最終的監測數據取為3 次觀測的平均值.數據分別采集自樁號K104+116-2.1、K104+126-1.2和K104+126-1.3.

2.2 隧道地表下沉量監測量

(1)樁號K104+116-2.1 傳感器

表1為隧道右線欒川端樁號K104+116-2.1 傳感器的地表下沉量監測數據.施工狀態的監測數據可以反映出隧道當前的安全狀態,若超出預警值則需要及時停止施工,重新評估設計方案及施工.但傳感器的監測數據是實時反映隧道當前安全指標,并不具備前瞻性和預測性.

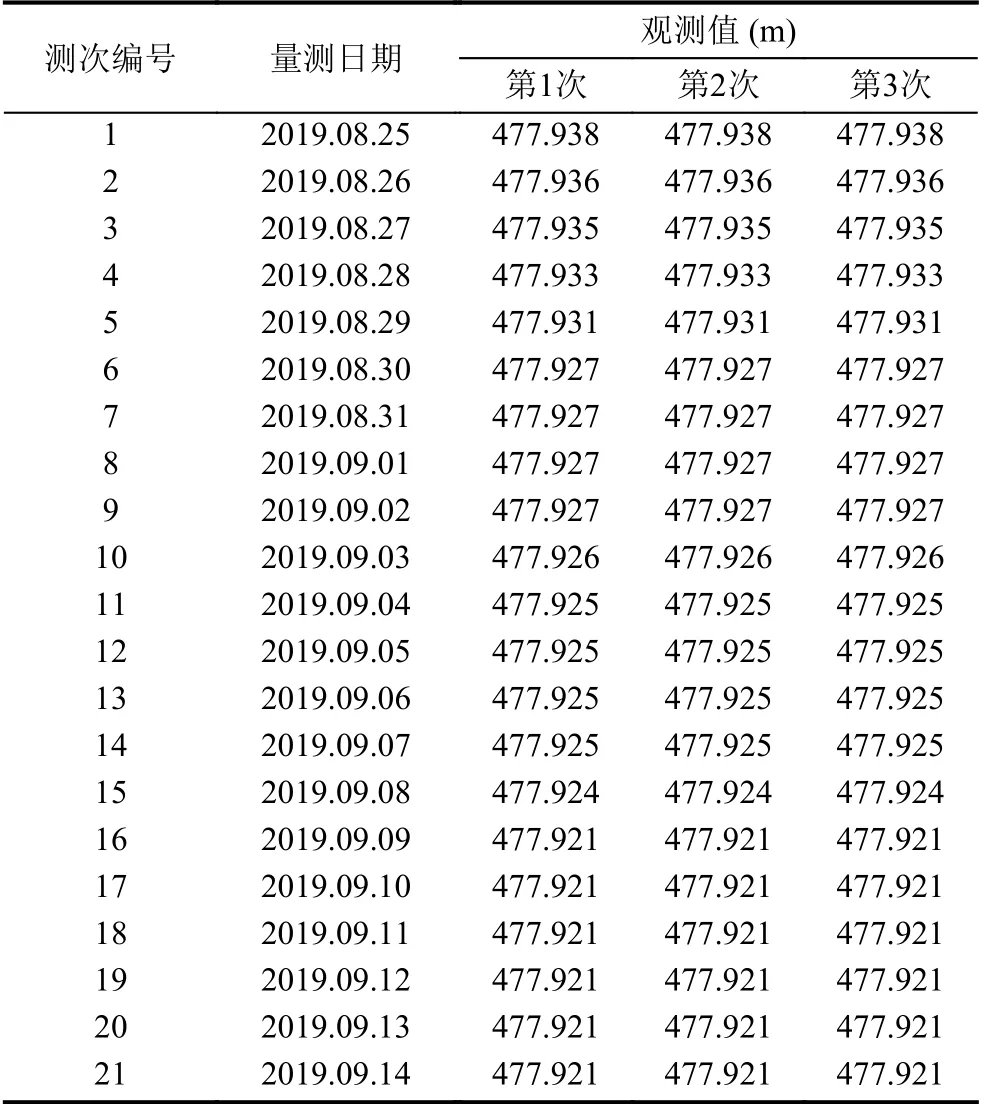
表1 隧道右線欒川端地表下沉量測記錄表(樁號K104+116-2.1)

(2)樁號K104+126-1.2 傳感器

表2為隧道右線欒川端樁號K104+126-1.2 傳感器的地表下沉量監測數據.在實際隧道施工中,傳感器需在各受力關鍵部位多點安放,來綜合反映出隧道總體情況.因此文中另選取同一隧道的不同部位傳感器進行監測分析.

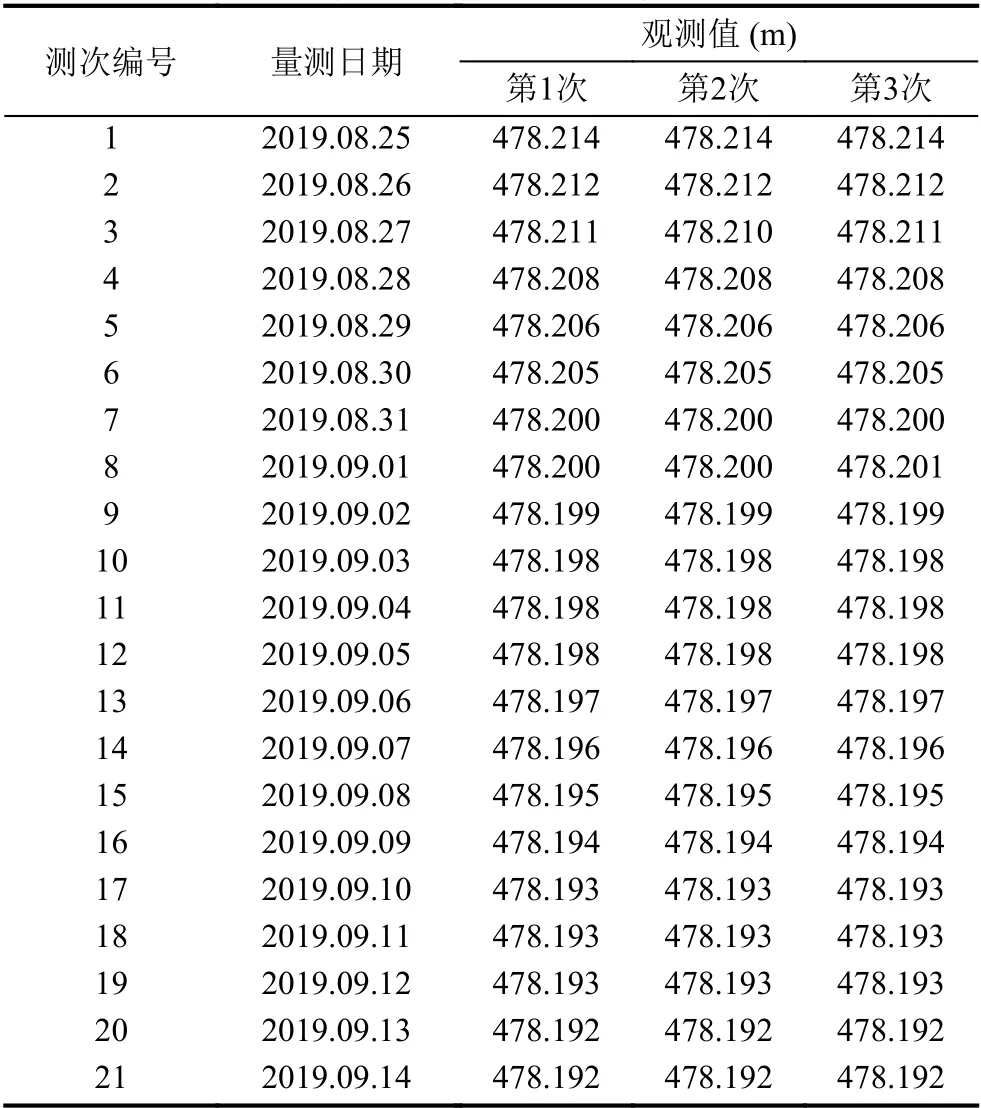
表2 隧道右線欒川端地表下沉量測記錄表(樁號K104+126-1.2)

(3)樁號K104+126-1.3 傳感器

表3為隧道右線欒川端樁號K104+126-1.3 傳感器的地表下沉量監測數據.為防止預測算法僅適用于特定傳感器數據,而不具有普適性,即出現過擬合現象.加設樁號K104+126-1.3 傳感器為預測結果進行驗證分析.

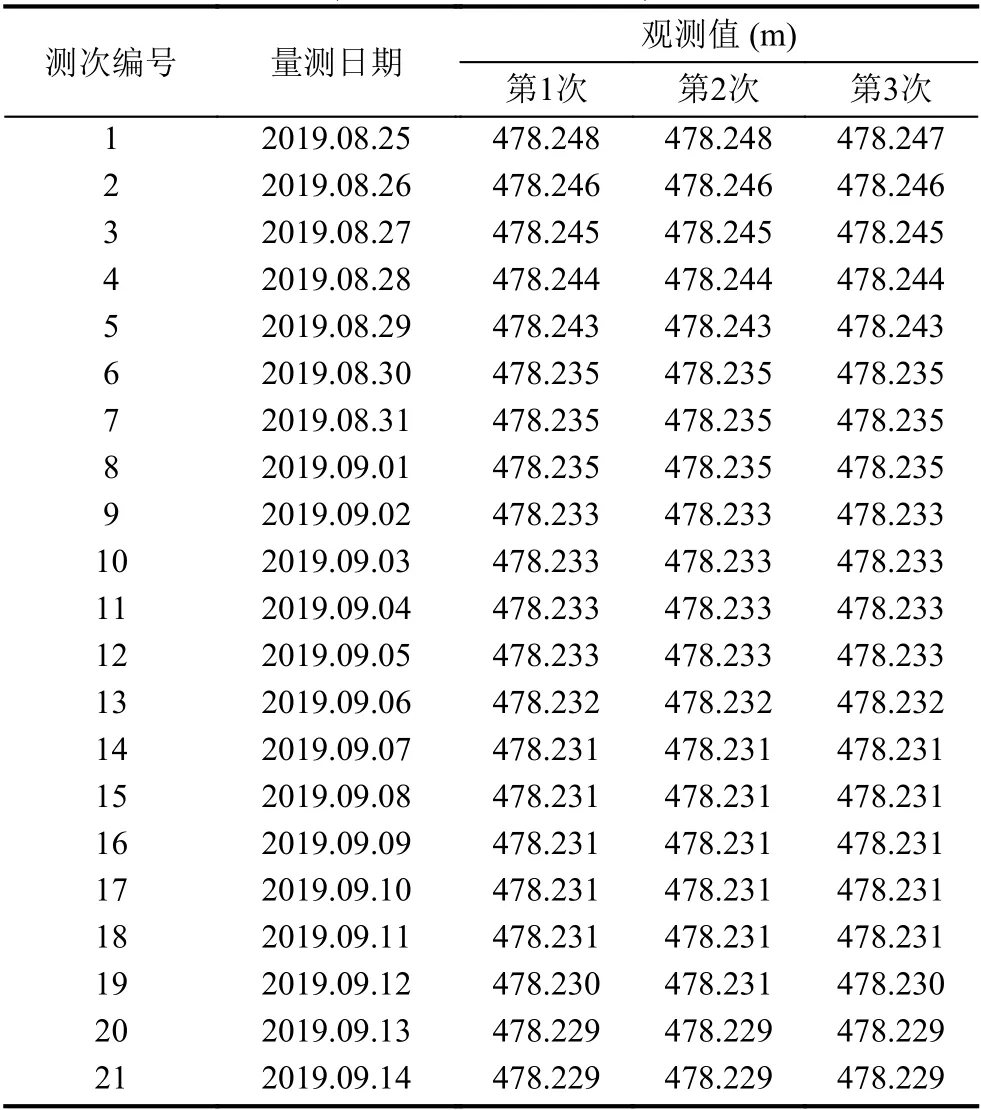
表3 隧道右線欒川端地表下沉量測記錄表(樁號K104+126-1.3)

3 結果與分析

圖3顯示了樁號K104+116-2.1 傳感器數據采用與預測結果.圖3(a) 分別對比了沉降量的觀測平均值、相對變化值與累計變化值的觀測量和相應的預測量.實線代表每天的實際觀測量,虛線代表依據歷史觀測數據預測到的沉降及其變化量.圖3(b)顯示神經網絡訓練曲線、最優訓練結果和目標,結果顯示在105 代達到了最優訓練表現,即0.009 510 5.圖3(c)顯示了神經網絡的訓練狀態,在105 代即結束代的梯度和學習率分別為0.017 479和1.678 3.圖3(d)為網絡回歸分析,結果顯示擬合數據與訓練數據間的相關度為0.971 5,即具有較高的相關性.

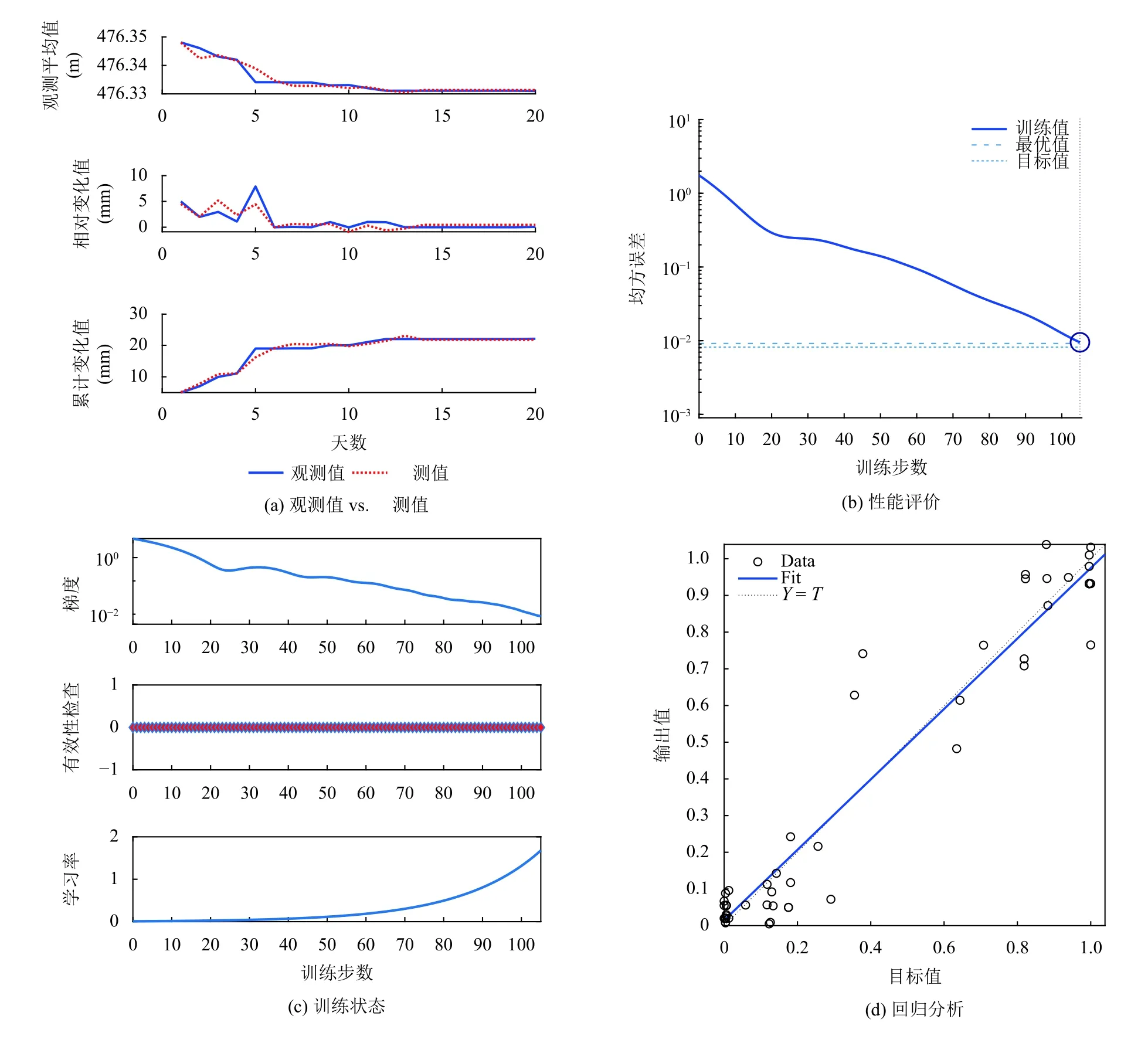
圖3 樁號K104+116-2.1 傳感器數據預測結果

為了確保所提預測模型的可靠性,另選擇樁號K104+126-1.2 傳感器數據進行驗證分析.圖4顯示了樁號K104+126-1.2 傳感器數據采用與預測結果.圖4(a)分別對比了沉降量的觀測平均值、相對變化值與累計變化值的觀測量和相應的預測量.實線代表每天的實際觀測量,虛線代表依據歷史觀測數據預測到的沉降及其變化量.圖4(b)顯示神經網絡訓練曲線、最優訓練結果和目標,結果顯示在122 代達到了最優訓練表現,相比于圖3的結果迭代次數有所延長.最優訓練結果為0.009 827 5,相比于圖3所示結果0.009 510 5,性能有輕微降低.圖4(c) 顯示了神經網絡的訓練狀態,在122 代即結束代的梯度和學習率分別為0.009 592 4和3.846 8,可以看出學習率相比于圖3(c)步長較長,可能在優化過程中產生了振蕩.圖4(d)為網絡回歸分析,結果顯示擬合數據與訓練數據間的相關度為0.950 24,總體來說仍具有較高的相關性.

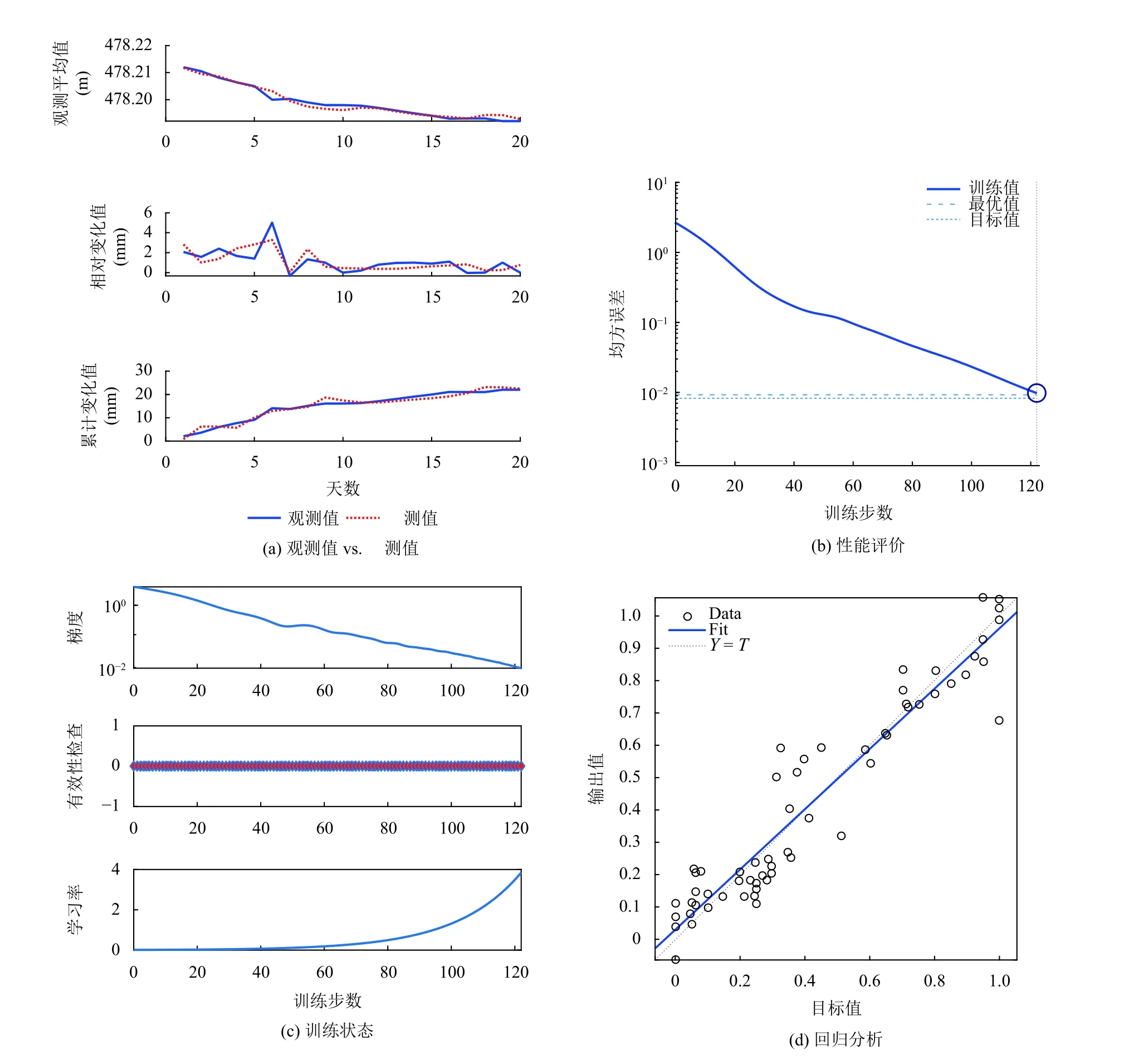
圖4 樁號K104+126-1.2 傳感器數據預測結果

同理,選擇樁號K104+126-1.3 傳感器數據進行驗證分析.圖5顯示了樁號K104+126-1.3 傳感器數據采用與預測結果.圖5(a)分別對比了沉降量的觀測平均值、相對變化值與累計變化值的觀測量和相應的預測量.實線代表每天的實際觀測量,虛線代表依據歷史觀測數據預測到的沉降及其變化量.圖5(b)顯示神經網絡訓練曲線、最優訓練結果和目標,結果顯示在333 代達到了最優訓練表現,訓練迭代次數均超出圖3和圖4所示結果.最優訓練結果為0.009 927 9.圖5(c)顯示了神經網絡的訓練狀態,在122 代即結束代的梯度和學習率分別為0.005 818 2和3.694 4,可以看出學習率相比于圖3(c)步長較長,可能在優化過程中產生了振蕩.圖5(d)為網絡回歸分析,結果顯示擬合數據與訓練數據間的相關度為0.961 93,相關性介于圖3與圖4之間,預測的魯棒性基本穩定.

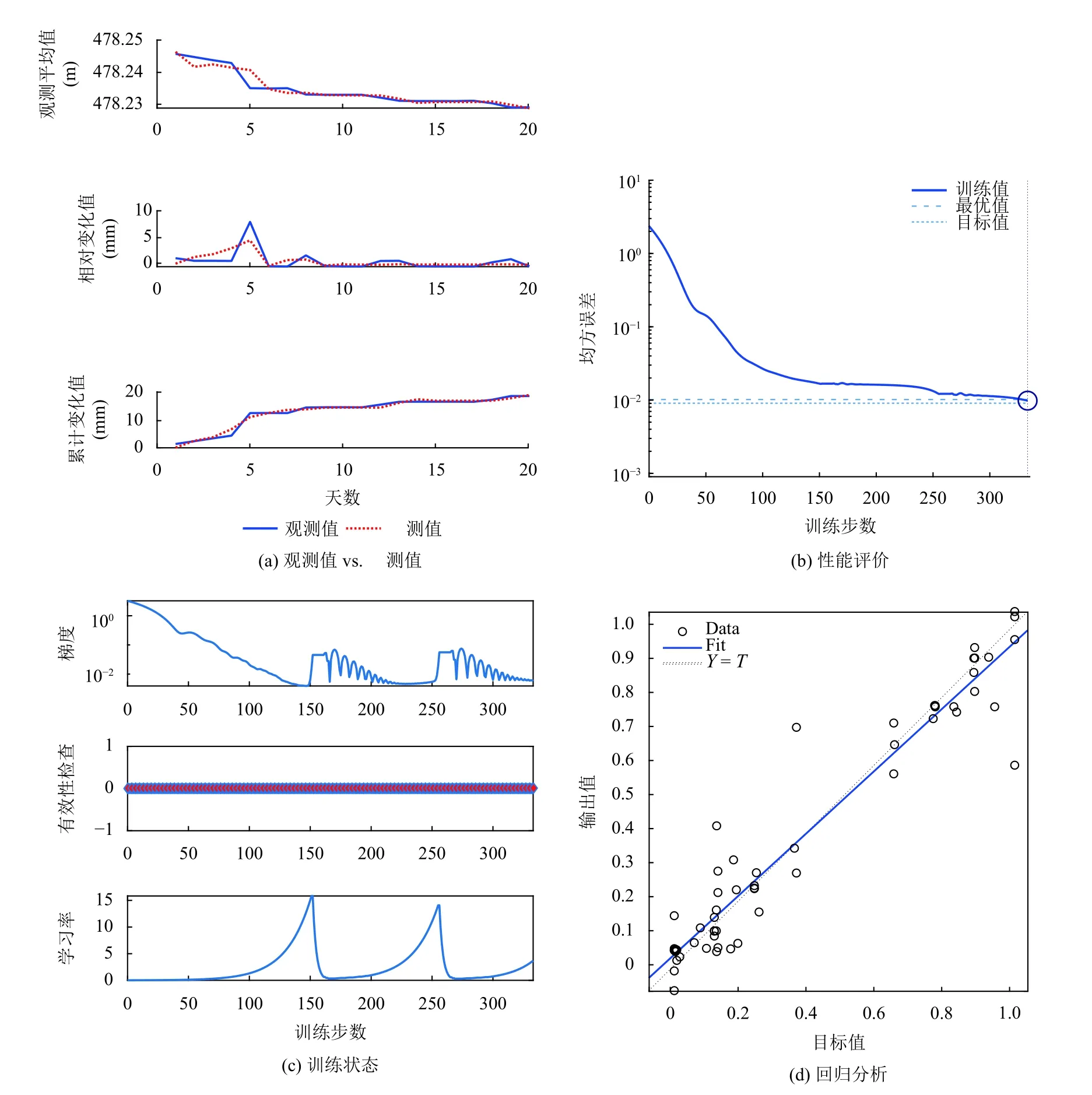
圖5 樁號K104+126-1.3 傳感器數據預測結果

綜上所述,針對樁號K104+116-2.1、樁號K104+126-1.2和K104+126-1.3的隧道地表沉降量傳感數據均有較準確的預測效果,且預測結果也具有一定的魯棒性,未出現過擬合情況,可應用于實際隧道施工的監測管理過程.

4 結論與展望

本文對時空特征區域神經網絡在施工隧道沉降量預測中的應用展開了深入的研究和分析,并以此提出了一種基于特征區域的神經網絡隧道狀態監測模型,且依據白家莊隧道實例地表下沉量對未來的演化趨勢做出合理預測,得出以下幾點結論.

(1)基于特征區域的神經網絡模型能夠有效融合多維空間特征量,預測結果具有精準性和魯棒性的特點,并能解決傳統神經網絡易出現過擬合的現象.

(2)基于特征區域的神經網絡模型相比于經典技術路線能更合理準確地預測出隧道地表下沉量,在隧道管理施工領域有一定應用價值.