太陽能電池鈣鈦礦材料模擬計算研究①
李達耀, 金成國, 黃偉新
(1.北部灣大學,廣西 欽州 535011; 2.廣西科技大學,廣西 柳州 545000)
太陽能具有無污染、分布廣泛、清潔等優點。 目前,較為常見的太陽能電池材料有無機硅金屬、鈣鈦礦等。 鈣鈦礦材料的結構式為ABX3,其中A、B、X分別為有機陽離子、金屬離子、鹵素基團。 鈣鈦礦材料具有促進太陽能利用的物理和化學特性,比如吸光性、電催化性等[1]。 鈣鈦礦太陽能電池有望引領未來太陽能電池的發展方向[2]。 但鈣鈦礦太陽能電池存在穩定性差、電池效率低等缺點,采用全無機鈣鈦礦摻雜結構是提高鈣鈦礦太陽電池材料性能的重要途徑。 本文從以下2個方面探討了不同類型摻雜對全無機鈣鈦礦光電性能和熱穩定性的影響:①鹵素摻雜結構對能帶和結構穩定性的影響;②B 位摻雜結構的光電性能分析,及其對材料缺陷形成的影響。 在此基礎上采用計算機模擬計算為合成具有高穩定性的晶體結構和高光電轉換效率的新型鈣鈦礦材料提供理論指導。
1 模擬計算理論
模擬計算相比傳統實驗而言,具有效率、準確度高等巨大優勢。 首先,模擬計算結果可以通過模型展示使研究人員對材料特性、材料各組分相關作用和材料在化學反應中的原理等有更好認識;其次,通過模擬計算可以減少實驗次數、節省時間,降低科研成本。
在模擬計算過程中采用第一性原理方法,只要知道普朗克常量、電荷量、光速、玻爾茲曼常數、電子質量就可以應用量子力學原理計算出體系的性質。 但由于計算機本身計算能力有限,模擬計算也有一個缺點,即對計算量的要求不能太高。 因此,計算時選用的材料對應的原子數目應相對較小。 BO 近似以及密度泛函理論等在電子與電子相互作用的相關效應和交換計算中十分常見。
1.1 BO 近似
處理分子或其他系統時考慮其在量子力學中的條件,系統的波函數需要通過解薛定諤方程或其他類似的偏微分方程來獲取。 根據Born-Oppenheimer 近似,考慮到電子與原子核之間質量存在巨大差距(通常原子核質量比電子大3 ~4個數量級)[3],電子的哈密頓量可根據BO 近似推斷為:H=T+U+V,其中T為動能,V為外場影響,U為庫倫作用。
1.2 密度泛函理論
密度泛函理論主要用于電子結構的研究,是計算鈣鈦礦材料電子結構必不可少的應用理論之一[4]。通常復雜多電子波函數都以常見的電子結構理論方法計算。 將復雜問題簡單化,是密度泛函理論的主要目的。 電子密度相對容易計算,而波函數計算則恰恰相反,用前者來代替后者,問題會變得簡單許多。 Kohn-Sham 方法是常見的密度計算方法,它可以將體系外部靜電勢中的電子相互作用引起的多體問題轉化為電子運動問題。 而對于其中交換相關性,現階段還沒有適當方法來解決與交換有關的能量問題[5]。 在非特定條件下,與量子力學中解決問題的方法相比,密度泛函理論給出的結果十分理想,并且通過固態計算可以有效降低計算成本[6]。
2 計算方法
Material Studio 軟件可以很好地進行原子替換、摻雜等應用操作,是一款十分實用的軟件[7-8],無論是結構優化、性能測試,還是材料摻雜和量子力學計算,其數據都較為準確。
2.1 CASTEP 計算方法
在CASTEP 計算中,總能量的計算尤為關鍵[9-10]。CASTEP 程序在密度泛函理論的基礎上通過計算得出的總能量分為3個部分:

式中ρ表示粒子的密度;T[ρ]表示一組密度為ρ而又沒有相互作用的粒子的動能;U[ρ]是根據庫侖相互作用得到的靜電能;Exc[ρ]包含了所有多體系統對總能量的貢獻[11]。
2.2 自洽計算
在CASTEP 計算中,平面波基函數在所有計算所需函數里是較為常見的。 由于哈密頓矩陣算符H還需要借助波函數C幫助完成運算,并不是獨立的,平面波基函數可作為自洽計算(SCF)的求解方程[12-13]。
3 鈣鈦礦材料計算
鈣鈦礦材料的結構式為ABX3,目前很有應用前景的無機鈣鈦礦材料為CsPbI3,本文對CsPbI3進行模擬計算。
3.1 鈣鈦礦材料CsPbI3 模型
通過參數設置、系統模擬,構建鈣鈦礦材料CsPbI3模型。 首先將各項晶格參數填好,之后根據需求將原子添加進去,初步完成CsPbI3的模型構建。 進行參數設置后,構建的CsPbI3模型如圖1 所示。 構建完成CsPbI3基礎模型后,對鈣鈦礦結構進行摻雜、原子清除或原子取代等計算,基于CsPbI3基礎模型,通過計算軟件構建新的模型。

圖1 CsPbI3 模型
3.2 鈣鈦礦材料計算參數
本文進行的是鈣鈦礦同質異構結構的計算,所以只以CsPbI3為例進行計算設置,后續的同質異構結構的計算都以之前設置的參數為基準。
3.2.1 計算參數
對于一個物理體系,能量分布決定了體系的狀態或材料的性能。 態密度實際上也就對應著能量分布,有了態密度,就可以根據統計力學得到想要的熱力學量。
構建完成CsPbI3結構模型后,用CASTEP 進行計算設置。 電荷密度由截止能決定,在計算中直接影響平面波個數及平面波的截止能。 在此次運算過程中,500 eV 作為一個判定能量值,代表截斷半徑的截止能,在500 eV 外的波函數變化與實際情況是一致的。

頻率在(ω,ω+dω)的模數可以通過其色散關系得出,結合態密度g(ω)的定義,可得:
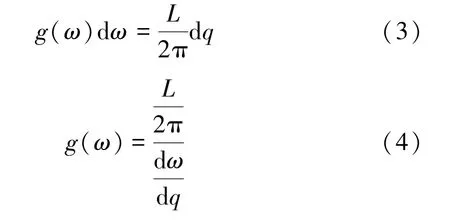
3.2.2 結構優化
在計算同質異構材料時,需要先對CsPbI3結構進行優化,當模擬CsPbI3結構中X 位的定量摻雜即X=F,Cl,Br,I的計算時,進行原子取代時可以在已有結構基礎上進行,這樣會大大降低工作量。
4 鈣鈦礦材料計算結果及分析
4.1 CsPbI3 同質異構體計算與結構分析
通過對不同結構的鈣鈦礦禁帶寬度和系統結合能進行對比,從而推斷不同組分鈣鈦礦材料的結構性能,進一步設計和優化其結構,提高光電轉化效率。
3種不同晶體結構CsPbI3如圖2~4 所示。

圖2 CsPbI3 單斜晶系結構

圖3 CsPbI3 斜方晶系結構

圖4 CsPbI3 立方晶系結構
表1 為各晶系晶格結構參數和能量參數。 由圖2~4及表1可以看出,不同晶系的晶胞大小不同,CsPbI3晶胞由大到小依次為立方晶系、單斜晶系、斜方晶系;單斜晶系的結合能最大,立方晶系的結合能最小,在晶系對稱性上,立方晶系對稱軸多,對稱性好[15]。

表1 CsPbI3 晶格的結構參數和能量參數
通過光子能量公式(式(5))以及物質波動量與其波長成反比關系(式(6)),可以根據帶隙寬度求得發光顏色。

式中h為普朗克常量;ν為光子頻率。
將式(6)代入式(5),可得:

通過式(7)計算得到CsPbI3單斜晶系、斜方晶系、立方晶系的波長分別為794.9 nm,492.1 nm,824.5 nm,可知斜方晶系帶隙的發光顏色為綠光,可作發光材料,而單斜晶系和立方晶系則適合做光電材料。
表2 為不同晶體結構中Pb 與I、Cs 與I 原子間距離。 由表2可知,Cs 和I 原子間距離最小的為單斜晶系;而Pb 和I 原子間距離最小的是立方晶系結構,并且單斜晶系與斜方晶系并沒有很大差異。
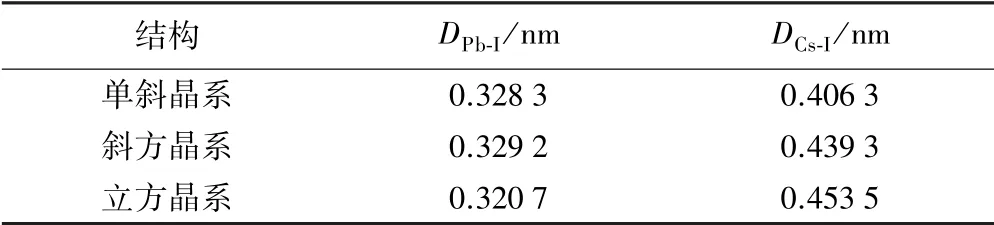
表2 CsPbI3 不同晶體結構中Pb 與I、Cs 與I 的原子間距離
態密度是指在一定能量范圍內其軌道(能級數)的數量。 對CsPbI3材料做能帶結構及態密度分析,軟件模擬下的CsPbI3材料不同晶體結構下的能帶間隙見圖5~7。 能帶間隙也稱為帶隙、能隙、禁帶寬度,是指一個能帶寬度,單位為eV。 由圖5 ~7可見,引入雜質后能隙會變小,但態密度沒有變化,這是因為摻雜原子質量太少,對電子的整體性質沒有很大影響。 對于整個體系而言,在能帶結構中引入了新能帶,但這個新能帶并不會引起決定性改變。

圖5 CsPbI3 單斜晶系的能帶結構

圖6 CsPbI3 斜方晶系的能帶結構

圖7 CsPbI3 立方晶系的能帶結構
4.2 X 位鹵素摻雜
對CsPbI3的X 位即I 用F、Cl、Br 摻雜,晶格能量參數計算結果如表3 所示。 從表3可以看出,禁帶寬度與系統結合能的絕對值存在正相關關系,禁帶寬度越大,其系統結合能的絕對值就越大。 在對CsPbI3的X 位摻雜時,替換F、Cl、Br 原子的結構能帶間隙越來越小,這說明摻雜原子半徑越小,材料禁帶寬度越大,系統結合能絕對值也越大。 其中,F 摻雜能大幅度提高帶隙,CsPbI3-F 帶隙值為2.659 eV,在太陽能光伏電板熒光材料選取中可以優先考慮;Br 摻雜CsPbI3-Br 帶隙值為1.749 eV,比較適合作為光伏電板光電材料。

表3 CsPbI3 的X 位摻雜時晶格能量參數
4.3 B 位摻雜
對CsPbI3的B 位即Pb 用Ca、Yb、Ba、Sn、Sr 摻雜,晶格參數計算結果如表4 所示。 根據表4可知,B 位摻雜對調節結合能具有作用,其中Ca 摻雜時結合能降低最為明顯。 B 位摻雜對帶隙有明顯調節作用,其中Sn 摻雜可使禁帶寬度降至1.184 eV。 受計算機限制,計算采用的超晶格模型較小,特別是對Yb 的摻雜,計算結果需要與實驗進一步對照。

表4 CsPbI3 的B 位摻雜時晶格的結構參數和能量參數
5 結 論
采用第一性原理計算和CASTEP 計算程序研究了CsPbI3的3種同質異構體和B 位、X 位摻雜對材料結構穩定性和能帶結構的影響,結果表明:
1) 根據模擬計算數據,3種同質異構體的結構穩定性依次為單斜結構、斜方結構、立方相結構。 CsPbI3單斜晶系、斜方晶系、立方晶系的波長分別為794.9 nm、492.1 nm、824.5 nm,斜方晶系帶隙的發光顏色為綠光,可作綠色光的發光材料,單斜晶系和立方晶系則適合作太陽能光伏電板的光電材料。
2) 對CsPbI3的X 位摻雜時, F 摻雜能大幅度提高帶隙,CsPbI3-F 的帶隙值為2.659 eV,在太陽能光伏電板熒光材料選取中可以優先考慮;Br 摻雜調節帶隙到1.7 eV,CsPbI3-Br 比較適合用作光伏電板光電材料。
3) B 位摻雜可以有效提高立方相穩定性,在實踐中可以通過B 位摻雜提高CsPbI3穩定性。 B 位摻雜對禁帶寬度有明顯調節作用,其中Sn 摻雜可使禁帶寬度降至1.184 eV;B 位摻雜對調節結合能有明顯作用,其中Ca 摻雜結構結合能降低最明顯。

