基于可射擊概率約束的防空作戰火力優化分配

智洪欣， 趙鵬， 李中， 彭祥新， 魯旭陽， 王琛

(陸軍炮兵防空兵學院鄭州校區， 河南 鄭州 450052)

0 引言

火力分配(WTA)作為防空作戰中的一個重要環節，能夠依據作戰任務、戰場實時態勢及武器裝備性能等因素，將空中來襲目標合理地分配給各防空火力單元，實現作戰效益最大化。因此，WTA問題是關系到作戰效能的決定性因素之一。

WTA問題主要涉及兩個步驟：一是綜合各種戰場因素進行數學建模，構建合理的目標函數和約束條件；二是根據構建的數學模型，采用合適的最優化方法進行最優化計算。其中，數學建模是核心，最優化計算是關鍵。針對這兩個步驟，已有大量研究，取得了豐碩成果。

文獻[2-5]提出了以聯合毀傷概率最大為目標的WTA模型，但是該模型忽視了火力資源消耗情況，在追求聯合毀傷概率最大的同時易造成火力資源浪費，致使防空系統無法提供持續有效的防空作戰能力。針對這一問題，文獻[6]在傳統模型中引入了聯合毀傷概率均值，即將聯合毀傷概率除以分配的火力單元總數，以盡可能少的火力資源消耗取得滿足閾值的聯合毀傷概率。文獻[7]構建了一個多目標優化模型，同時將最大聯合毀傷概率和最小分配火力單元數作為目標函數進行優化。文獻[8-10]通過設置約束條件限制攔截同一目標的火力單元數，盡可能減少火力資源消耗。文獻[6-10]單純從數量上限制火力資源消耗，未考慮目標距離所分配火力單元射擊區的距離，即未考慮目標到火力單元的飛臨時間，生成的分配方案易貽誤戰機。針對該問題，文獻[11]提出一種基于先期毀傷準則的WTA模型，在保證聯合毀傷概率的前提下，以盡量少的火力資源消耗優先攔截飛臨時間短的目標。文獻[2-11]分別提出了基于不同約束條件最大化聯合毀傷概率的WTA模型，然而這些模型都忽略了一個事實：只有在防空武器對來襲空中目標可以射擊的前提下，計算聯合毀傷概率、約束火力資源消耗、約束目標飛臨時間等才有實際意義。

另外，WTA問題本質上是整數型非線性組合優化問題，屬于一種NP難問題，目前常用群智能優化算法求解。文獻[2]采用遺傳算法求解WTA問題。文獻[11]提出了一種混沌和粒子群混合優化算法，以提高算法的全局搜索能力。文獻[12]改進了布谷鳥算法，引入了移民算子和柯西變異算子等，采用貪婪方式逐維更新，以提高算法的局部和全局搜索能力。綜合分析這些算法，都不同程度地存在易陷入局部最優值、收斂速度慢或者算法設計復雜、實現困難等問題，不能滿足戰場實際要求，有待進一步提升。Faramarzi等受控制容積質量平衡物理現象的啟發，提出了一種新的智能優化算法，平衡優化器(EO)算法。該算法控制參數少、魯棒性強，易于實現，在多個標準函數測試中表現出較高的優化性能。然而，該算法未能有效平衡全局搜索與局部搜索能力，在一定程度上限制了算法的收斂速度，且增大了尋得全局最優值的難度。

針對以上問題，本文提出一種基于可射擊概率約束的WTA模型，該模型在基于先期毀傷準則模型的基礎上，引入了基于空襲強度和火力單元轉火時間的可射擊概率約束，從而使模型更貼近戰場實際。在此基礎上，提出一種非線性自適應慣性權重的改進EO算法。該算法首先采用Tent映射方法代替原算法中的隨機方法初始化種群，實現種群多樣性；其次，在位置更新公式中引入非線性自適應慣性權重，來平衡算法的全局搜索和局部搜索能力，加快收斂速度、提高求解精度。

1 基于可射擊概率約束的WTA模型

假設在某次防空戰斗中有批來襲空中目標，編號為(=1,2,…,)，進入個火力單元的責任防區，編號為(=1,2,…,)。令表示決策變量，其含義為：若分配火力單元攔截來襲空中目標，則=1，否則=0；令表示火力單元攔截來襲空中目標的毀傷概率，為火力分配方案對目標的聯合毀傷概率，則

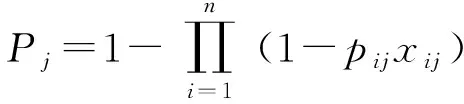
(1)

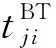
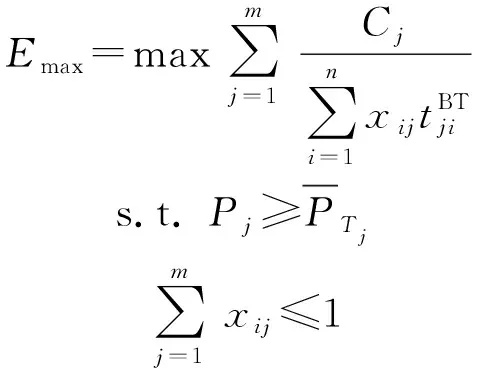
(2)

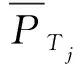
該模型在確保滿足聯合毀傷概率閾值的前提下，以盡量少的火力資源消耗，優先分配威脅度大、飛臨時間短的目標。但是，該模型忽略了聯合毀傷概率只有在火力單元對來襲空中目標可以射擊的前提下才有實際意義的事實。因此，本文提出一種基于可射擊概率約束的WTA模型。

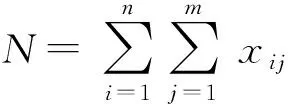
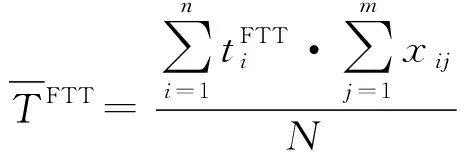
(3)

令表示空襲強度，根據排隊論中的愛爾蘭公式可得分配方案的可射擊概率為

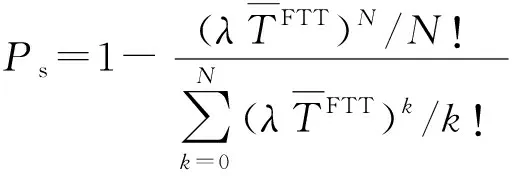
(4)

則基于可射擊概率約束的WTA模型為

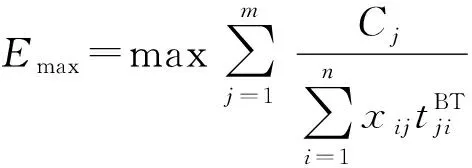
(5)

式中：為可射擊概率閾值，可由指揮員根據戰場態勢確定。

從(5)式中可以看出，該模型保存了原基于先期毀傷準則模型的優勢，即在滿足聯合毀傷概率閾值的前提下，以盡量少的火力資源消耗，優先分配威脅度大、飛臨時間短的目標。同時也引入了基于空襲強度和火力單元轉火時間的可射擊概率，使聯合毀傷概率計算具有實際意義，使模型更貼近戰場實際。

由于(5)式帶有非線性約束，在最優化計算過程中屬于求解有約束的優化問題，本文采用罰函數法將其轉化為一個求解無約束優化問題，設計罰函數如下：

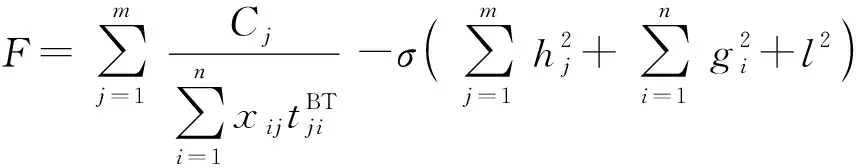
(6)

式中：為罰參數，表示懲罰的力度，開始為一個較小的正數，隨著迭代次數逐漸增加到一個很大的值。

因此，把求有約束的優化問題轉化為如下求解無約束優化問題：

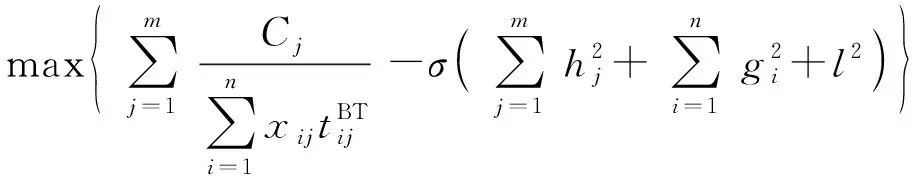
(7)

(7)式是一個無約束優化問題，求得的最優解會使、和為0，因此(7)式的最優解是(5)式的最優解。

2 基于非線性自適應慣性權重的EO算法

2.1 標準EO算法

EO算法是一種模擬環境工程中控制容積完全混合(流入和流出控制體積的體積流量相同)的質量動態平衡物理現象(質量衡算)的智能優化算法，將控制容積內的濃度作為問題的解。

完全混合的質量動態平衡常用質量平衡方程描述為

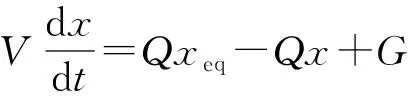
(8)

式中：為控制容積；為控制容積內的濃度；為流入、流出控制容積的流體體積；為平衡狀態(控制容積內無質量生成)下的濃度；為控制容積內的質量生成速率。

(8)式描述了控制容積中質量流入、流出和生成過程中動態平衡的內在機理，對該1階微分方程求解，可得

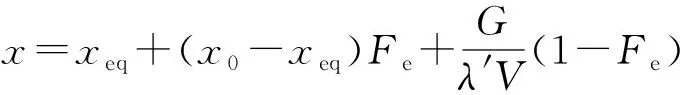
(9)

式中：為控制容積在時刻的濃度，即初始濃度；為指數項；′為流動率。

EO算法將(9)式進行優化改造后作為解向量更新公式，改造后的公式為

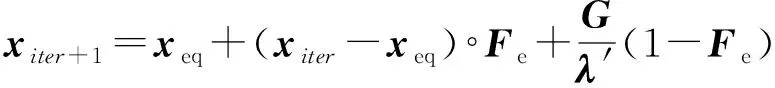
(10)

式中：為迭代次數；為當前解；為全局最優解；+1為更新后的解；′表示取值范圍為[0，1]的隨機數向量。

算法將當前4個最優解(,,,)以及它們的均值()組成平衡池：={,,,,}，在迭代計算中，(10)式中的全局最優解以相同概率從平衡池中選擇，增強了算法的全局搜索能力。

為加強算法的局部搜索能力，算法將質量生成速率設計為

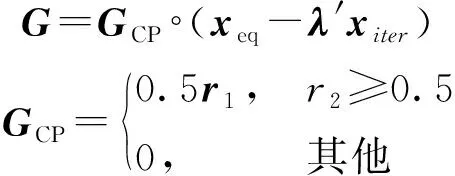
(11)

式中：為生成速率控制參數；為取值范圍為(0，1)區間的隨機數向量；為(0，1)區間的隨機數。

同時為了平衡算法的局部搜索和全局搜索能力，改造為

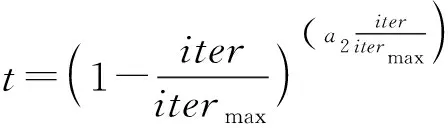
(12)

式中：為控制全局搜索能力的常系數，設置為2；sign(·)為符號函數；為取值范圍為[0，1]的隨機數向量；為最大迭代次數；為控制局部搜索能力的常系數，設置為1，EO算法通過和平衡全局搜索和局部搜索能力。

2.2 基于混沌序列的初始方法

有研究表明，初始種群對智能優化算法的優化效率有較大影響，分布均勻、多樣性好的初始種群可以提高算法的收斂速度乃至提高算法的求解精度。然而，EO算法采用在搜索空間內隨機生成的方式產生初始種群。這種隨機生成的方式容易導致初始種群分布不均勻、多樣性差。針對這一不足，本文提出使用Tent混沌映射產生初始種群，增強種群的多樣性，從而提高算法效率。

Tent混沌映射的數學表達式為

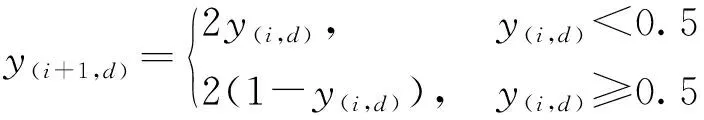
(13)

式中：為生成的混沌序列；為種群數量；為解的維度。

利用Tent混沌映射產生初始種群的主要思路是：首先根據(13)式生成混沌序列，然后將生成的混沌序列線性映射到解空間作為算法的初始種群。Tent混沌映射具有較好的遍歷均勻性和隨機性，因此使用Tent混沌映射產生的初始種群可以提高優化算法性能。

2.3 非線性自適應慣性權重

通常，智能優化算法在初期側重于全局搜索，以便快速到達最優解附近；在后期則側重于局部搜索，在最優解附近進行精確搜索。因此，算法性能在很大程度上取決于平衡全局搜索和局部搜索的能力。EO算法主要通過指數項來平衡，然而從解更新公式(10)式中可以看到，只作用于后兩項，算法完全繼承了最優解，僅依靠并不能有效平衡算法的局部搜索能力和全局能力。因此，本文提出在解更新公式(10)式中引入非線性自適應慣性權重，作用于最優解，與指數項配合共同協調算法的局部搜索和全局搜索能力，從而提高算法的性能。

基于非線性自適應慣性權重的解更新公式為

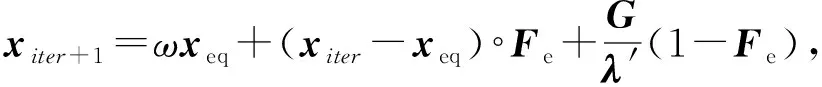
(14)

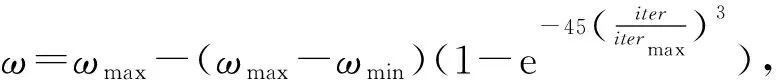
(15)

式中：和分別為慣性權重的初值和終值，本文設置為09和04，則隨迭代次數的變化曲線如圖1所示。

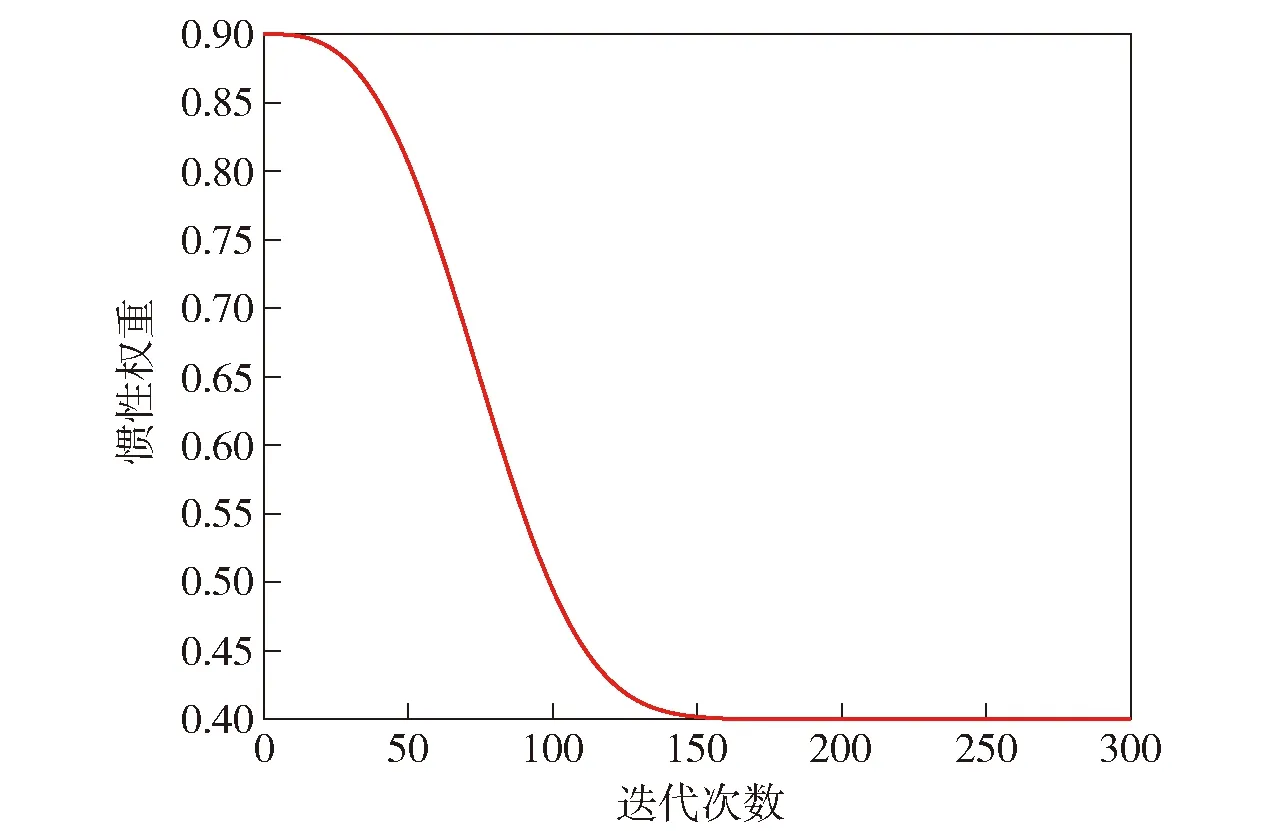
圖1 慣性權重變化曲線Fig.1 Change curve of inertia weight

從圖1中可以看出，慣性權重是迭代次數的非線性遞減函數，在迭代初期和迭代末期遞減速度相對較慢，從而使算法在迭代初期的一段時間能夠保持較大的慣性權重，增強了算法全局搜索能力；在迭代后期的一段時間保持了較小的權重，增強了算法的局部搜索能力。由此可見，非線性自適應慣性權重提高了算法平衡局部搜索和全局搜索的能力，進而提高了算法的性能。

本文提出的改進EO算法流程圖(見圖2)主要步驟如下：

種群數量，迭代次數，解的維度；

全局最優解以及相應的適應度值。

初始化參數，=2，=1，=09，=04，=1，=-inf，=-inf，=-inf，=-inf

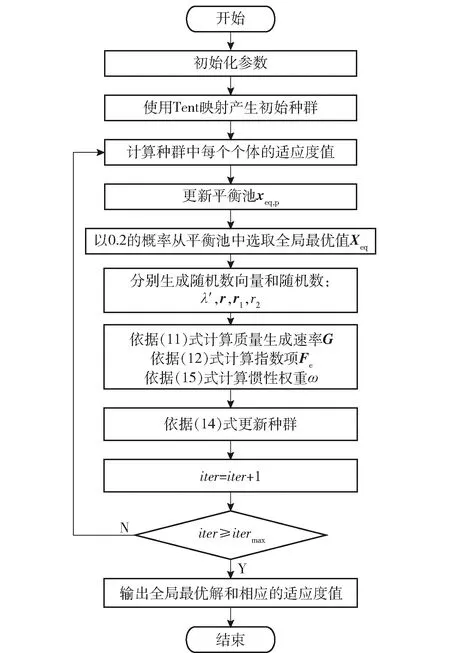
圖2 基于非線性自適應慣性權重的EO算法流程圖Fig.2 Flow chart of EO algorithm based on nonlinear adaptive inertia weight

使用Tent映射在解空間內產生初始種群。

計算種群中每個個體的適應度值。

比較適應度值，計算并更新平衡池：

={,,,,}。

以02的概率從平衡池中隨機選出全局最優解

分別生成隨機數向量′、、和隨機數

依據(11)式計算質量生成速率，依據(12)式計算指數項，依據(15)式計算慣性權重

依據(14)式更新種群。

=+1

判斷是否達到最大迭代次數，若達到則停止計算，輸出最優解以及相應的適應度值；否則，轉步驟3。

3 算例仿真計算及結果分析

為驗證本文基于可射擊概率的WTA模型的優點，以及所提基于非線性自適應慣性權重EO算法的有效性，進行算例仿真計算。

3.1 仿真設置

仿真配置為Intel(R) Core(TM) i7-6700 CPU，8 GB內存，Windows 7操作系統，利用MATLAB 2019b軟件進行仿真計算。

假設在某次防空戰斗中有8批來襲空中目標，進入10個火力單元的責任防區，各個目標的威脅度為=[060 070 035 056 081 076 066 083]，目標到火力單元的飛臨時間為

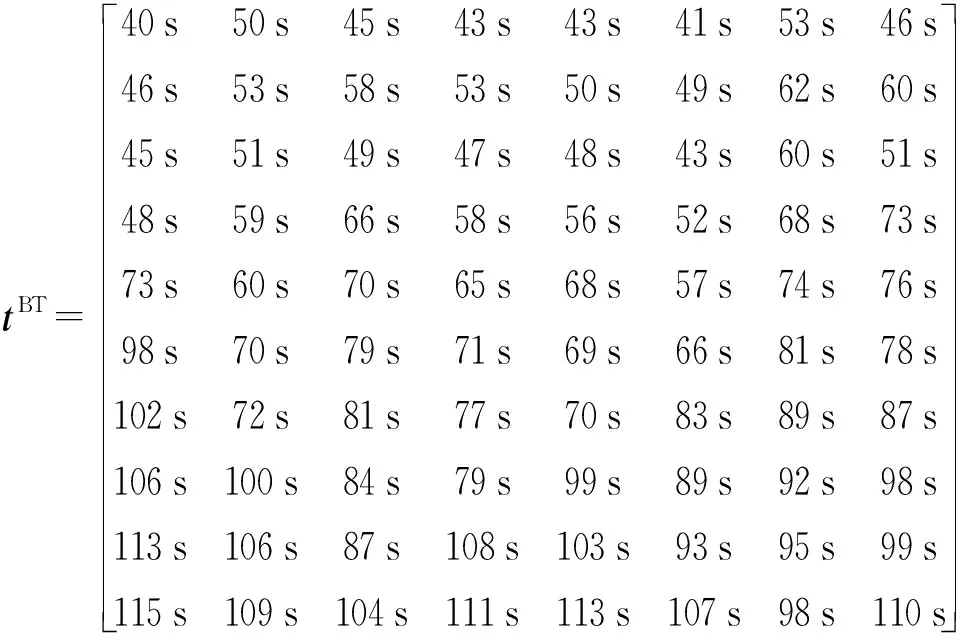
各火力單元對來襲目標的毀傷概率為

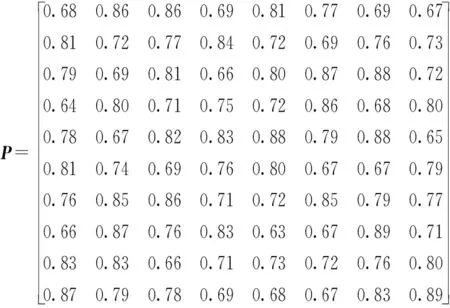
各火力單元的轉火時間為

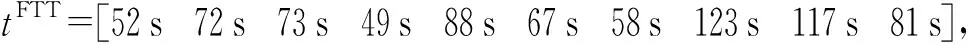
空襲強度設置為與來襲空中目標數相同：=8架min；預期聯合毀傷概率閾值設置為08，可射擊概率閾值設置為07，種群數設置為30，最大迭代次數為300

3.2 仿真計算結果及分析

3.2.1 模型有效性驗證

分別基于本文提出的基于可射擊概率約束的防空火力分配模型(以下簡稱Model 1)以及文獻[11]提出的防空火力分配模型(以下簡稱Model 2)，使用改進的EO算法進行火力優化分配，分配結果如表1、表2所示。

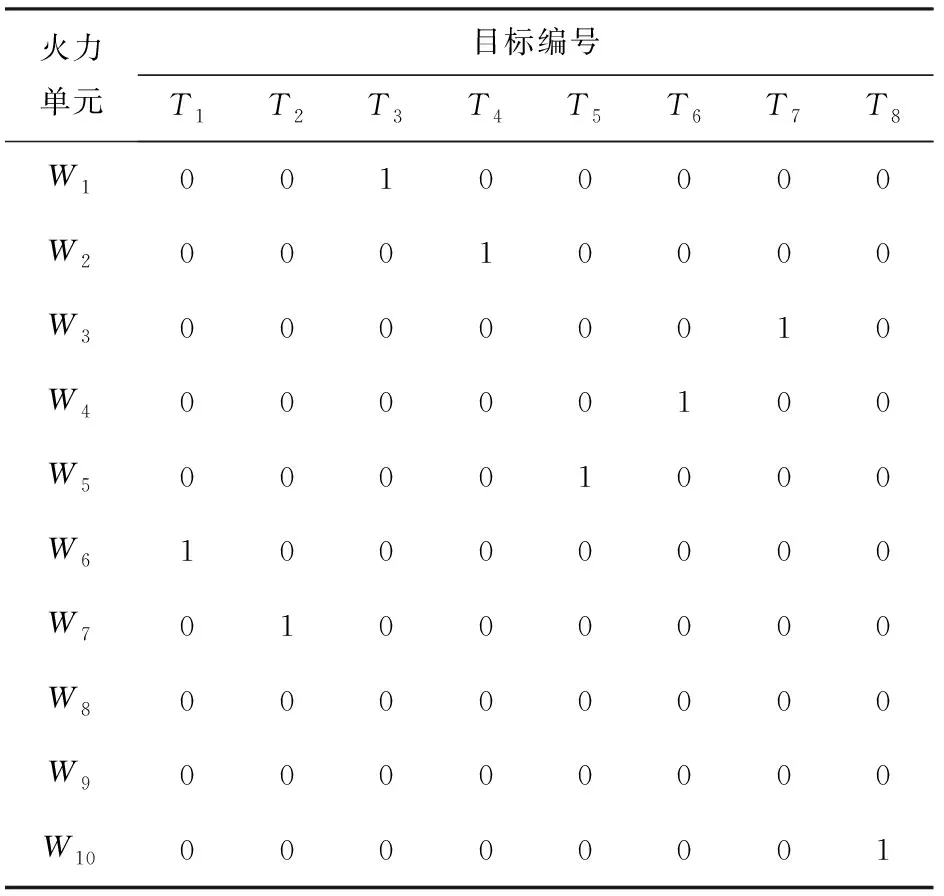
表1 Model 1的分配方案

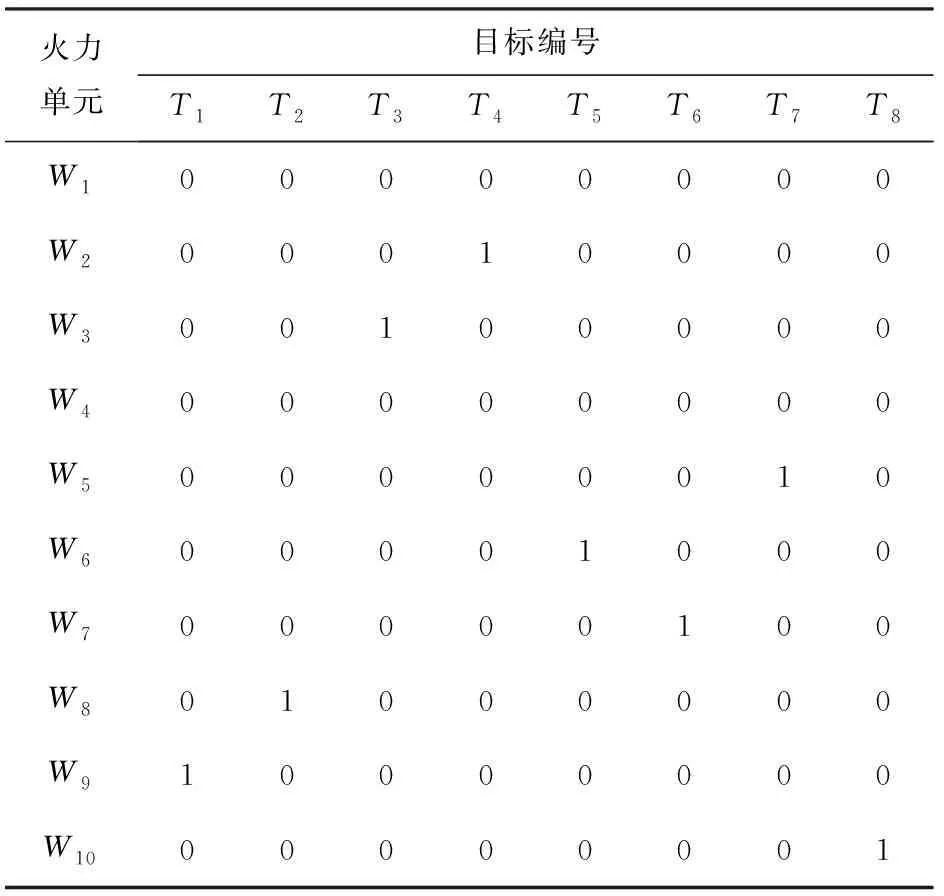
表2 Model 2的分配方案

從表1和表2中可以看到，Model 1和Model 2均能夠約束火力資源消耗，分別選用8個火力單元攔截來襲的8個目標，節約火力資源，為防空系統提供持續作戰能力。兩種分配方案的聯合毀傷概率和性能分別如表3、表4所示。

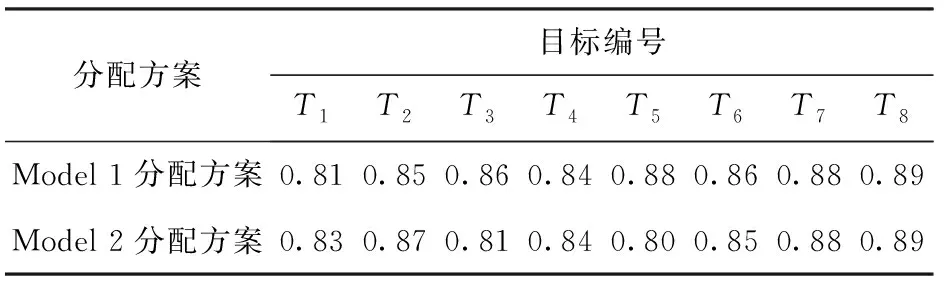
表3 分配方案聯合毀傷概率

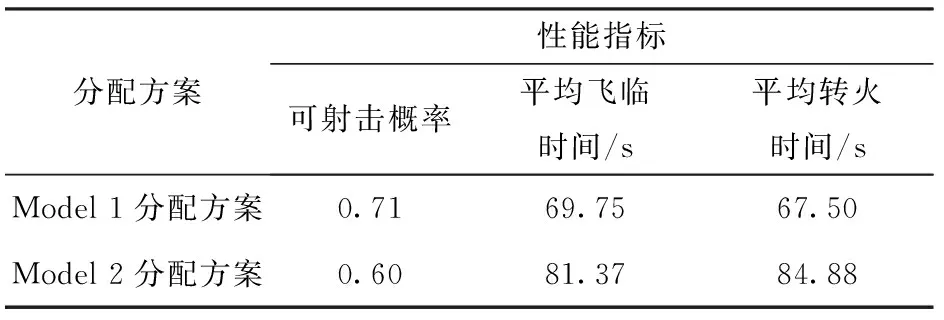
表4 分配方案性能

從表3中可以看到，兩種模型的分配方案均滿足設定的聯合毀傷概率閾值0.8. 從表4中可以看出：Model 1分配方案的可射擊概率為0.71，滿足指揮員設定的閾值要求，但是Model 2分配方案的可射擊概率為0.60，沒有達到設定的閾值；Model 1分配方案的平均飛臨時間和平均轉火時間均比Model 2分配方案的短，表明Model 1在可射擊概率的約束下，能夠有效平衡聯合毀傷概率和平均轉火時間，且能夠優先使用反應快的火力單元攔截飛臨時間短的目標。上述仿真結果驗證了本文提出的基于可射擊概率約束的WTA模型優點。

3.2.2 優化算法有效性驗證

為檢驗本文提出的基于非線性自適應慣性權重EO算法的性能，分別使用原始EO算法和改進后EO算法進行仿真計算，最大迭代次數為300，種群數量為30，算法隨迭代次數的收斂情況如圖3所示，算法最優適應度值如表5所示。

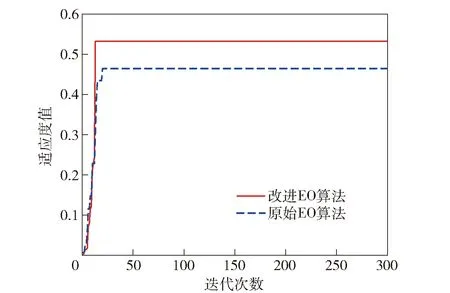
圖3 適應度值隨迭代次數的變化Fig.3 Change of fitness with iterations

表5 算法的最優適應度值

從圖3以及表5中可以看出，改進后EO算法和原始EO算法均能收斂至全局最優解，然而改進后EO算法在收斂速度上和適應度值上都明顯優于原始算法，表明非線性自適應慣性權重能夠有效平衡算法的局部與全局搜索能力，從而提高算法的尋優效率。

3.2.3 與其他WTA優化算法比較

為進一步驗證本文算法的有效性，分別與粒子群優化算法和遺傳算法進行對比計算。其中，遺傳算法中的雜交概率設置為0.9，變異概率設置為0.04，粒子群優化算法的學習因子設置為2.05，3種算法的最大迭代次數均設置為300，種群數量均設置為30。各算法隨迭代次數的收斂情況如圖4所示。

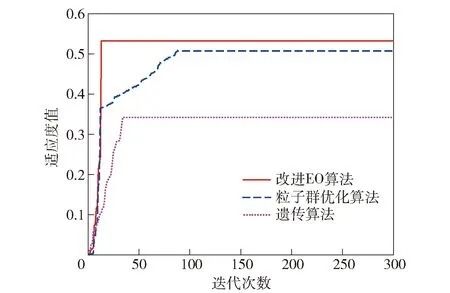
圖4 與其他WTA優化算法對比Fig.4 Comparison of the proposed algorithm and other WTA optimization algorithms

從圖4中可見：本文所提算法收斂速度最快，遺傳算法次之，粒子群優化算法最慢；本文所提算法最優適應度值優于粒子群優化算法，粒子群優化算法優于遺傳算法，表明本文所提算法在收斂速度和最優適應度值兩方面均優于粒子群優化算法和遺傳算法，進一步驗證了本文基于非線性自適應慣性權重的EO算法的有效性。

4 結論

本文針對WTA問題建模中未考慮可射擊因素的問題，建立一種基于可射擊概率約束的防空作戰火力優化分配模型；提出了一種基于非線性自適應慣性權重的改進平衡優化器優化算法，對該模型進行求解。通過仿真實驗，得到以下結論：

1)在WTA模型中加入可射擊概率約束，可在模型中融入影響防空作戰的空襲強度、火力單元轉火時間等多種因素，使WTA模型更加貼近戰場實際。仿真結果表明，該模型能夠在保證滿足可射擊概率和聯合毀傷概率閾值的前提下，優先使用反應快的火力單元攔截飛臨時間短的目標，并盡量減少火力資源消耗，為防空系統提供持續作戰能力。

2)優化算法在初期側重于全局搜索，在后期則側重于局部搜索，非線性自適應慣性權重能夠引導EO算法更好地平衡局部搜索和全局搜索能力，進而提高尋優能力。