Q690D和Q460D鋼板對接焊縫的疲勞壽命計算

黃益洲, 王萬禎*, 李草原

Q690D和Q460D鋼板對接焊縫的疲勞壽命計算

黃益洲1, 王萬禎1*, 李草原2

（1.寧波大學 土木與環境工程學院, 浙江 寧波 315211; 2.寧波大學 海運學院, 浙江 寧波 315832）

采用新近提出的統一計及疲勞裂紋形成壽命和穩定擴展壽命的結構鋼疲勞壽命計算模型, 對Q690D和Q460D鋼板對接焊縫疲勞試驗進行疲勞壽命計算. 假設高強鋼板對接焊縫的疲勞裂紋起裂于對接焊縫邊緣, 沿板寬擴展且穿透板厚, 可將高強鋼板對接焊縫疲勞斷裂面積分為疲勞裂紋穩定擴展面積f和失穩擴展面積n(即名義最大應力作用下的凈截面強度拉斷面積). 以結構鋼的橢球面斷裂模型為判據, 由高強鋼板對接焊縫疲勞裂紋的裂尖真實應力場解得高強鋼板對接焊縫疲勞裂紋的失穩擴展面積n、穩定擴展面積f和穩定擴展長度f. 計算結果表明: 不同屈服強度下的高強鋼板對接焊縫的疲勞壽命相差較大, 應采用各自量化的疲勞壽命計算式; 本文量化的結構鋼疲勞壽命計算式對Q690D和Q460D鋼板對接焊縫疲勞試驗壽命的計算誤差為-63.9%～-0.2%, 而現行規范建議的疲勞壽命計算式的計算誤差為-70.7%～68.0%; 本文量化的結構鋼疲勞壽命計算式的計算精度高于規范建議的疲勞壽命計算式, 前者計算結果對所有試件均偏于安全, 后者計算結果對部分試件偏于不安全, 且部分試件過于保守.

高強鋼板; 對接焊縫; 疲勞壽命計算模型; 疲勞裂紋; 穩定擴展

隨著鋼材生產工藝的提高, 高強鋼在建筑結構中得到應用, 我國《鋼結構設計標準》規范新增了Q460高強鋼[1]. 高強鋼已成為鋼結構領域的研究熱點, 但對高強鋼焊縫疲勞性能的研究非常有限[2-5]. 仇立寧等[6]分析了高碳鋼滾動接觸疲勞失效機理, 朱春莉等[7]研究了GCr15鋼接觸表面塑性形變強化與裂紋萌生機制, 鄭榮躍[8]提出了疲勞裂紋擴展曲線的微分方程擬合法, 但以上研究均未涉及高強鋼焊縫疲勞壽命計算.

由于對結構鋼及焊縫疲勞裂紋形成、擴展至斷裂全過程的極限狀態及有關影響因素的研究還不足, 我國現行《鋼結構設計標準》[1]采用式(1)建議的應力幅準則和允許應力法計算結構鋼及焊縫的疲勞壽命, 而以前的《鋼結構設計規范》[9]則采用最大應力準則來驗算結構鋼及焊縫的疲勞破壞.

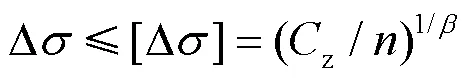
結構鋼及焊縫的疲勞破壞雖然積累了豐富的試驗資料, 也能通過計算預估疲勞壽命, 但仍較多地依賴經驗, 理論上并未真正解決[10].

結構鋼疲勞破壞一般可分為疲勞裂紋形成、穩定擴展和失穩擴展三個階段. 但結構鋼焊縫不存在裂紋形成階段[10-11], 因為焊縫在施焊時不可避免地存在氣孔、夾渣、欠焊等缺陷, 這些缺陷即為初始裂紋(起裂源). 考慮到疲勞裂紋失穩擴展是瞬間斷裂, 因此結構鋼的疲勞壽命一般按疲勞裂紋形成壽命和擴展壽命之和計算, 前者如基于局部應力-應變法的Neuber模型[12], 后者如基于名義應力幅的Paris-Erdogan模型[13], 疲勞裂紋形成和擴展階段分界線取裂紋長度0.02～0.05mm. 但應看到結構鋼疲勞裂紋的形成和擴展是一個連續、漸變、完整、統一的自然演化(失效)過程, 有采用統一的疲勞壽命計算模型描述其總疲勞壽命的可能. 另外, 取疲勞裂紋長度0.02～0.05mm作為疲勞裂紋形成和擴展階段的分界線, 很大程度上取決于裂紋觀測儀器的靈敏度, 如采用更靈敏的裂紋觀測儀器(如0.005、0.01mm), 應能觀測到更小裂紋尺寸的疲勞裂紋形成和擴展階段分界線.

眾所周知, 疲勞裂紋隨循環加載次數增加而加速擴展, 即同樣的疲勞裂紋擴展長度在循環加載早期和后期, 或人為劃分的疲勞裂紋形成和擴展階段, 所需的循環加載次數會相差較大. 若疲勞裂紋形成和擴展階段分界線裂紋長度取值不同, 如0.02、0.05mm等, 則因疲勞裂紋形成和擴展階段采用不同的疲勞壽命計算模型, 也勢必導致計算的總疲勞壽命相差較大.

基于上述考慮, 本文采用文獻[14]提出的統一計及疲勞裂紋形成壽命和穩定擴展壽命的結構鋼疲勞壽命計算模型對Q690D和Q460D鋼板對接焊縫疲勞試驗進行疲勞壽命計算, 驗證其計算精度和普適性.

1 高強鋼板對接焊縫的疲勞壽命計算模型

1.1 高強鋼板對接焊縫的疲勞壽命計算式

疲勞裂紋擴展速率是決定高強鋼板對接焊縫疲勞壽命的關鍵因素, 受到了廣泛關注[4-5,12-13,15-23].

文獻[14]基于結構鋼疲勞裂紋隨加載次數加速擴展的試驗事實, 以結構鋼疲勞裂紋的穩定擴展速率(一次循環加載下疲勞裂紋擴展長度)為循環加載次數的單調遞增冪函數為假定, 即雙對數坐標系下高強鋼疲勞裂紋的穩定擴展速率是循環加載次數的單調遞增線性函數, 積分導出統一計及疲勞裂紋形成壽命和穩定擴展壽命的結構鋼疲勞壽命計算模型:

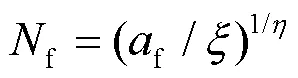
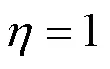
式(2)建議的結構鋼疲勞壽命計算模型克服了《鋼結構設計標準》[1]建議的疲勞壽命計算式, 即式(1)等式兩端量綱不同的缺陷.

參數、取決于鋼種、試件幾何形狀(應力集中程度)、載荷參數等, 由疲勞試驗數據擬合標定.

1.2 高強鋼板對接焊縫的疲勞裂紋穩定擴展長度

圖1和圖2是文獻[3]進行的Q460D鋼板對接焊縫疲勞的試驗照片. 由圖可見, 疲勞斷裂面分為貝紋狀的疲勞裂紋穩定擴展區和粗糙的疲勞裂紋失穩擴展區; 疲勞裂紋萌生于焊接熱影響粗粒區或熔合區, 呈放射狀向板側邊擴展且穿透板厚. 圖2的對接焊縫疲勞斷口電鏡掃描照片顯示, 疲勞斷口分為疲勞裂紋源、疲勞裂紋穩定擴展和瞬斷區, 疲勞裂紋穩定擴展區斷面光滑, 有向外放射狀疲勞條帶, 撕裂棱將不同晶粒間的疲勞條帶相連; 瞬斷區有明顯的韌窩和解理臺階.

圖1 Q460D鋼板對接焊縫的疲勞試驗破壞照片

圖2 對接焊縫疲勞斷口電鏡掃描照片

基于圖1與圖2所示的Q460D鋼板對接焊縫的疲勞試驗結果[3], 假設高強鋼板對接焊縫的疲勞裂紋起源于對接焊縫一側邊的焊接熔合區, 向對接焊縫另一側邊擴展, 且穿透焊縫厚度. 則高強鋼板對接焊縫的疲勞裂紋穩定擴展長度(f)為:

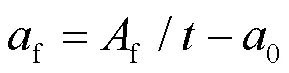
式中:為對接焊縫厚度;0為初始缺陷尺寸;f為疲勞裂紋穩定擴展面積.

1.3 高強鋼板對接焊縫的疲勞裂紋穩定擴展面積

按前所述, 高強鋼板對接焊縫的疲勞斷裂面分為貝紋狀的疲勞裂紋穩定擴展區和粗糙的疲勞裂紋失穩擴展區, 則包含初始裂紋或缺陷尺寸0效應的疲勞裂紋穩定擴展面積為(f):

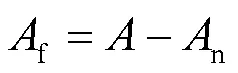
式中:為對接焊縫全截面斷裂面積;n為疲勞裂紋失穩擴展面積.

1.4 高強鋼板對接焊縫的疲勞裂紋失穩擴展面積

為計算高強鋼板對接焊縫的疲勞裂紋失穩擴展面積n, 需求解高強鋼板對接焊縫疲勞裂紋的裂尖真實應力場, 并選用能描述高強鋼板對接焊縫疲勞裂紋裂尖在復雜應力狀態下的斷裂判據.

文獻[24]以結構鋼在三向等拉伸應力狀態下斷裂和屈服近似重合為保守假設, 提出的結構鋼橢球面斷裂模型及耦聯的橢球面屈服模型分別為:

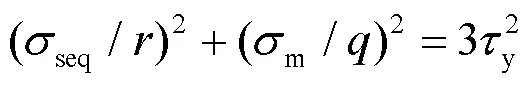
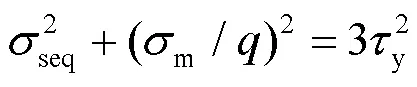
y、u、f和分別為疲勞裂紋裂尖的Mises等效應力、平均應力、對接焊縫的剪切屈服強度、剪切斷裂強度、單向拉伸屈服強度、單向拉伸極限強度、單向拉伸斷裂強度和泊松比.

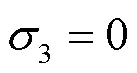
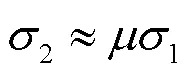
則高強鋼板對接焊縫疲勞裂紋裂尖應力場為:

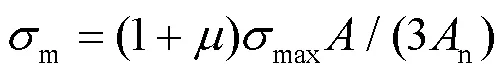
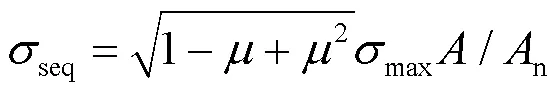
將式(7)計算的高強鋼板對接焊縫疲勞裂紋裂尖應力場代入式(5)建議的結構鋼橢球面斷裂模型, 解得高強鋼板對接焊縫的疲勞裂紋失穩擴展面積:

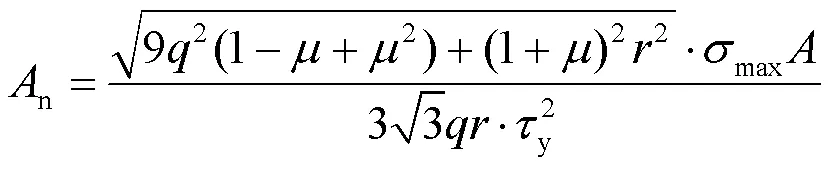
2 高強鋼板對接焊縫的疲勞壽命計算

文獻[2-3]對圖3所示的厚度為8mm的Q690D和Q460D軋制鋼板“V”形坡口全焊透對接焊縫進行了疲勞試驗, Q690D和Q460D鋼板采用的焊條分別為CHE857Cr和CHE557RH, 均采用手工電弧焊焊接, 焊后保留焊縫余高, 焊縫質量等級為一級. 疲勞試驗前經查, 各試件對接焊縫無微裂紋等明顯缺陷.

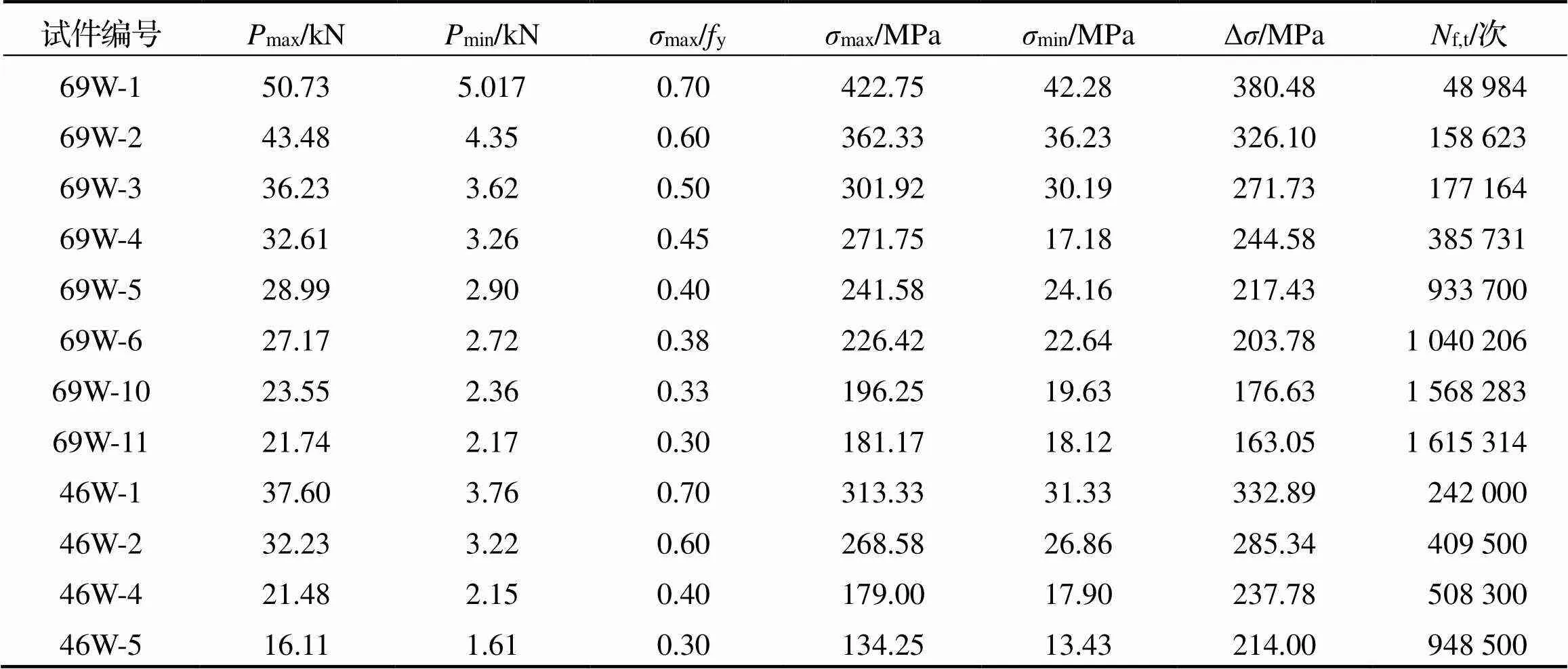
表1 Q690D和Q460D鋼板對接焊縫疲勞試驗加載參數和試驗結果

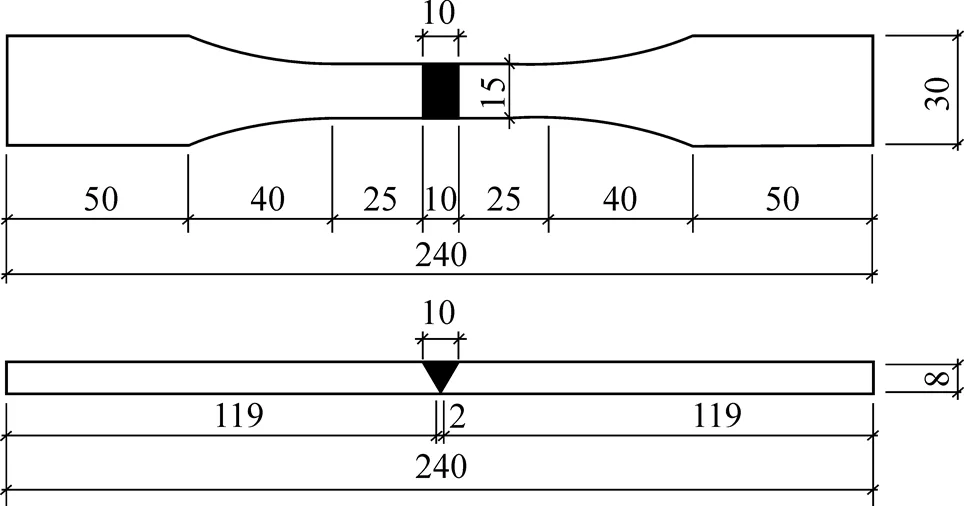
圖3 Q690D和Q460D鋼板對接接頭試件尺寸(mm)

疲勞試驗結果顯示, Q690D和Q460D鋼板對接焊縫的疲勞壽命具有較大離散型, 但仍表現出明顯規律, 即疲勞壽命隨應力幅的增加而降低.

篩選出符合疲勞壽命隨應力幅的增加而降低規律的Q690D和Q460D鋼板對接焊縫疲勞試驗試件, 其試驗結果列于表1, 其中,f,t為疲勞壽命試驗值. 需要說明的是, 為區分Q690D和Q460D試件并盡量保持文獻[2-3]中對接焊縫試件的原始編號, 表1對Q690D和Q460D試件進行重新編號, 如試件69W-1對應文獻[2]中的Q690D鋼板對接焊縫試件B-1, 其余相同.

表2 Q690D和Q460D鋼板對接焊縫材性數據

橢球面斷裂模型參數.

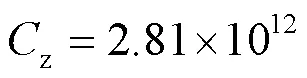
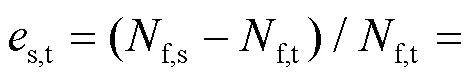
將式(2)建議的高強鋼板對接焊縫的疲勞壽命計算模型改寫為雙對數坐標:

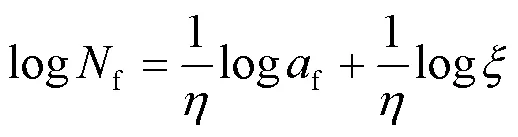
按式(9)對表3中各試件疲勞壽命試驗值f,t和疲勞裂紋穩定擴展長度f進行擬合, 結果如圖4所示, 并且Q690D和Q460D鋼板對接焊縫的疲勞壽命計算模型參數、的標定結果列于表3. 由表可見, 參數、隨對接焊縫強度變化較大, 不同屈服強度的高強鋼板對接焊縫應采用不同的疲勞壽命計算模型參數.

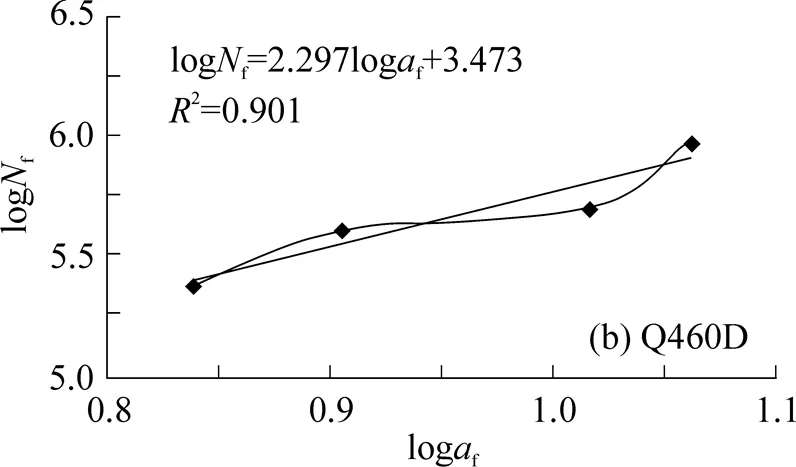
圖4 鋼板對接焊縫af和Nf的擬合函數

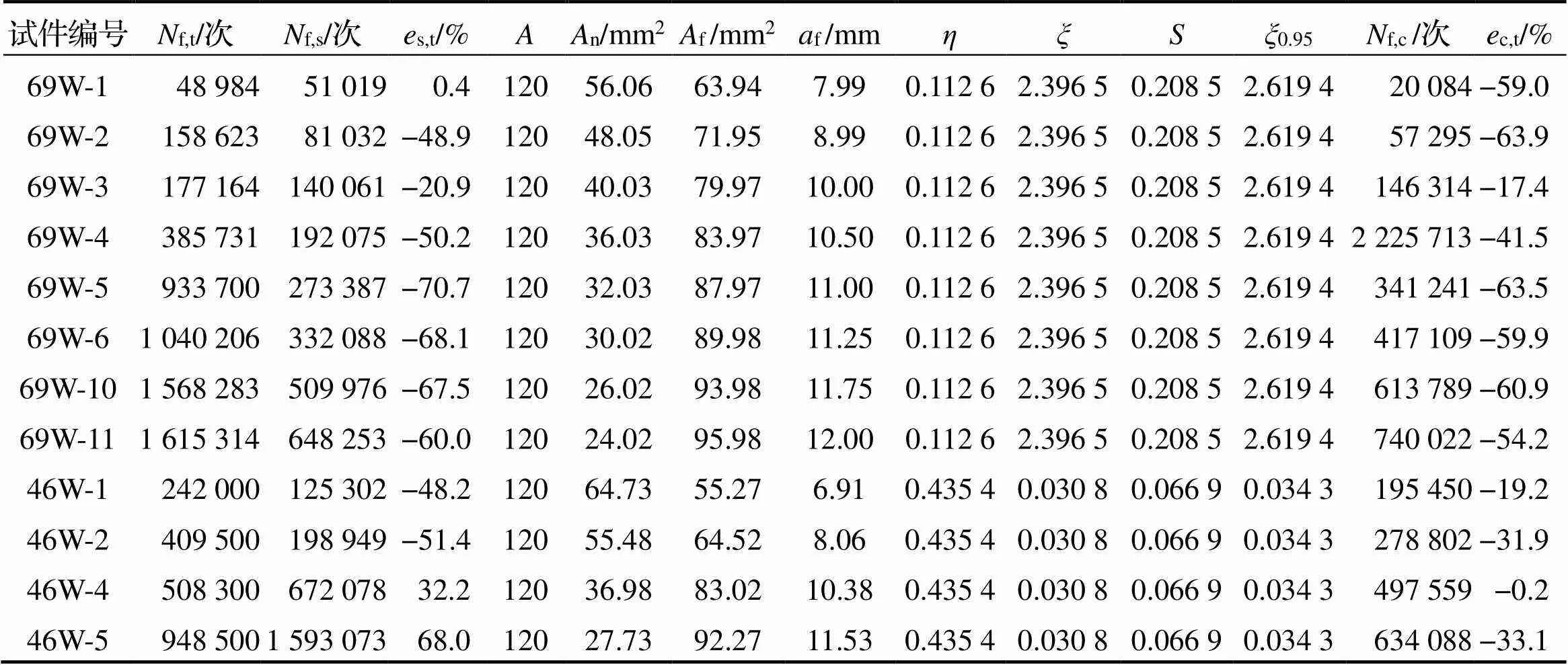
表3 Q690D和Q460D高強鋼開孔板的疲勞壽命計算模型參數標定

在式(9)中引入各試件疲勞壽命計算值的1.645倍標準差,得式(10). 對表3中各試件的疲勞壽命試驗值f, t和疲勞裂紋穩定擴展長度f按式(10)重新擬合(圖5), 得95%保證率的高強鋼板對接焊縫的疲勞壽命計算模型參數0.95(表3).

再按式(10)計算各試件疲勞壽命f,c及與試驗值的相對誤差c,t, 由表3可見, 式(10)建議的高強鋼板對接焊縫的疲勞壽命算式對Q690D和Q460D鋼板對接焊縫的疲勞壽命計算偏于安全, 與試驗值的相對誤差為-63.9%～-0.2%, 計算精度高于《鋼結構設計標準》[1]的計算結果.

3 結論

采用統一計及疲勞裂紋形成壽命和穩定擴展壽命的結構鋼疲勞壽命計算模型對Q690D和Q460D鋼板對接焊縫進行疲勞壽命計算, 得到以下結論: (1)量化的高強鋼板對接焊縫疲勞壽命算式對Q690D和Q460D鋼板的計算誤差為-63.9%～ -0.2%; (2)現行設計規范建議的疲勞壽命計算式對Q690D和Q460D鋼板的計算誤差為-70.7%～68.0%. (3)量化的結構鋼疲勞壽命算式對Q690D和Q460D鋼板的計算精度高于規范建議的疲勞壽命計算式, 前者計算結果對所有試件均偏于安全, 后者計算結果對部分試件偏于不安全, 部分試件過于保守.

[1] GB50017-2017. 鋼結構設計標準[S].

[2] 郭宏超, 萬金懷, 劉云賀, 等. Q690D高強鋼焊縫連接疲勞性能試驗研究[J]. 土木工程學報, 2018, 51(9):1-9.

[3] 郭宏超, 郝李鵬, 李炎隆, 等. Q460D高強鋼及其焊縫連接疲勞性能試驗研究[J]. 建筑結構學報, 2018, 39(8): 157-164.

[4] 宗亮, 施剛, 王元清, 等. WNQ570橋梁鋼及其對接焊縫疲勞裂紋擴展性能試驗研究[J]. 工程力學, 2016, 33 (8):45-51.

[5] 施剛, 張建興. 高強度鋼材Q460C及其焊縫的疲勞性能試驗研究[J]. 建筑結構, 2014, 44(17):1-6.

[6] 仇立寧, 李淑欣, 蔣港輝, 等. 無碳化物貝氏體高碳鋼滾動接觸疲勞失效分析[J]. 寧波大學學報(理工版), 2021, 34(2):55-60.

[7] 朱春莉, 趙鳳平, 蘇云帥. GCr15鋼接觸表面塑性形變強化與裂紋萌生機制[J]. 寧波大學學報(理工版), 2019, 32(6):61-66.

[8] 鄭榮躍. 疲勞裂紋擴展曲線的微分方程擬合法[J]. 寧波大學學報(理工版), 2004, 17(3):264-267.

[9] TJ17-74. 鋼結構設計規范[S].

[10] 沈祖炎, 陳揚驥, 陳以一. 鋼結構基本原理[M]. 2版. 北京: 中國建筑工業出版社, 2005:66-77.

[11] 陳紹蕃, 顧強. 鋼結構(上冊)—–鋼結構基礎[M]. 北京: 中國建筑工業出版社, 2003:301-315.

[12] Neuber H. Theory of stress concentration for shear- strained prismatical bodies with arbitrary nonlinear stress- strain law[J]. Journal of Applied Mechanics, 1961, 28(4): 544-550.

[13] Paris P C, Erdogan F. A critical analysis of crack growth laws[J]. Journal of Basic Engineering, 1963, 85:528-534.

[14] 王萬禎. Q345圓鋼桿的疲勞破壞模型[J]. 哈爾濱工業大學學報, 2019, 51(12):121-127.

[15] Foeman R G, Kearney V E, Eegle R M. Numerical analysis of crack propagation in cyclic-loaded structure [J]. Journal of Basic Engineering, 1967, 89(3):459-464.

[16] Elber W. The significance of fatigue crack closure[C]. Damage tolerate in aircraft structures, ASTM STP 46, Philadelphia: American Society for Testing and Material, 1971:230-242.

[17] 王春生, 段蘭, 鄭麗, 等. 橋梁高性能鋼HPS 485W疲勞裂紋擴展速率試驗研究[J]. 工程力學, 2013, 30(6): 212-216.

[18] 楊冰, 趙永翔, 梁紅琴, 等. 基于Elber型方程的隨機疲勞長裂紋擴展概率模型[J]. 工程力學, 2005, 22(5): 99-104; 125.

[19] 趙永翔, 楊冰, 張衛華. 一種疲勞長裂紋擴展率新模型[J]. 機械工程學報, 2006, 42(11):120-124.

[20] 關鵬濤, 閭川陽, 唐夏燾, 等. Q345R鋼多個過載作用下疲勞裂紋擴展行為研究[J]. 工程力學, 2017, 34(7): 224-231; 240.

[21] 趙興華, 蔡力勛, 包陳. CRO試樣的疲勞裂紋擴展行為試驗方法研究[J]. 工程力學, 2016, 33(11):20-28.

[22] 黃學偉, 蔡力勛, 包陳, 等. 基于低周疲勞損傷的裂紋擴展行為數值模擬新方法[J]. 工程力學, 2011, 28(10): 202-208.

[23] 劉艷萍, 陳傳堯, 李建兵, 等. 14MnNbq焊接橋梁鋼的疲勞裂紋擴展行為研究[J]. 工程力學, 2008, 25(4):209- 213.

[24] 王萬禎. 結構鋼開裂準則及斷裂試驗分析[J]. 工程力學, 2008, 25(5):27-31.

[25] 施剛, 林錯錯, 周文靜, 等. 460MPa高強鋼箱形截面軸壓柱局部穩定有限元分析和設計方法研究[J]. 工程力學, 2014, 31(5):128-136.

Fatigue life calculation of butt weld of Q690D and Q460D steel plates

HUANG Yizhou1, WANG Wanzhen1*, LI Caoyuan2

( 1.School of Civil and Environmental Engineering, Ningbo University, Ningbo 315211, China; 2.Faculty of Maritime and Transportation, Ningbo University, Ningbo 315832, China )

The test fatigue life of butt weld of Q690D and Q460D steel plates was calculated by using a newly proposed fatigue life calculation model of structural steel, which takes into account the fatigue crack forming life and stable growth life. It is assumed that the fatigue crack of butt weld of high strength steel plates starts from the edge of butt weld and propagates along the width of plate and penetrates the thickness of plate. The fatigue fracture areaof butt weld of high strength steel plates was divided into two parts: the stable propagation areafof fatigue crack and the unstable propagation areanof fatigue crack (i.e. the tensile fracture area under the nominal maximum stress). The instability propagation arean, stable propagation areafand stable propagation lengthfof fatigue crack of butt weld of high strength steel plates were calculated according to the true stress field of fatigue crack tip by using an elliptical fracture model of constructional steel as fracture criterion. The calculation results show that the fatigue life of butt weld of high strength steel plates with different yield strength is quite different, and should be calculated by their own quantitative fatigue-life formula. The calculation error of the quantitative fatigue life calculation formula in this paper is -63.9% – -0.2% for the fatigue life of butt weld of Q690D and Q460D steel plates, while the calculation error of fatigue life formula recommended by current code is -70.7% – 68.0%. The calculation accuracy of the quantitative fatigue life calculation formula in this paper is higher than that recommended by current code. The former is safe for all specimens, while the latter is unsafe for some specimens and too conservative for others.

high strength steel plate; butt weld; fatigue life calculation model; fatigue crack; stable propagation

通信作者:王萬禎（1974－）, 男, 河南周口人, 博士/教授, 主要研究方向: 鋼結構斷裂與疲勞. E-mail: wangwanzhen1975@sina.com

TU391

A

1001-5132（2022）03-0032-06

2021?03?04.

浙江省基礎公益技術研究計劃（LGF18E080007）.

黃益洲（1997－）, 男, 浙江臺州人, 在讀碩士研究生, 主要研究方向: 鋼結構. E-mail: 936961204@qq.com

寧波大學學報（理工版）網址: http://journallg.nbu.edu.cn/

（責任編輯 章踐立）