電磁差速耦合輪對導向機理*

李濤濤，劉建新

（西南交通大學 牽引動力國家重點實驗室，成都 610031）

由于獨立旋轉車輪的兩側車輪是完全獨立旋轉的，其自動對中能力和曲線通過能力較差的導向問題催生了耦合輪對的提出。所謂耦合輪對，就是通過某種耦合方式將同一輪對上的兩側車輪間形成一定的耦合聯系。

自從Benington［1］提出耦合輪對概念后，國內外許多學者也提出各自的耦合輪對技術方案。諸如：彈性阻尼耦合器式［2］、磁力可控耦合器式［3］、磁流體耦合器 式［4］、電軸耦合式［5］以及干摩擦副式［6］。以上各種耦合輪對技術方案提出后，其導向性能一直是領域內各位學者關注的焦點。王軍平［7-8］分析了彈性—阻尼耦合輪對的耦合剛度和耦合阻尼對車輛系統的直線穩定性和曲線通過性能的影響，并確定了最佳耦合度的取值范圍。Ma等人［9］在分析彈性阻尼耦合輪對縱向振動特性中，發現彈性阻尼耦合輪對的兩側車輪的耦合導致輪軸扭轉振動，這一振動引起兩側輪縱向蠕滑力的不同，進而導致輪對縱向顫振現象。文獻［10］分析了磁流體耦合輪對轉向架前后輪對的耦合度對曲線通過性能的影響規律，并對同一轉向架的前后輪對耦合度進行優化配置。根據摩擦限滑差速器的結構建立了橫向摩擦耦合輪對的力學模型，Leng H等人［11］研究了摩擦耦合輪對的曲線性能和臨界轉速，并分析了摩擦力矩對動態性能的影響。文獻［12］基于摩擦副耦合輪對的理論模型提出了一種根據輪對橫向位移設計摩擦扭矩的方法，結果表明摩擦副耦合輪對具有傳統剛性輪對相似的導向性能。以上研究表明耦合輪對具有比獨立旋轉車輪更好的導向性能，同時，以上各種耦合輪對形式均是通過某種耦合方式實現兩側車輪轉速同步，從而使得輪軌處可以產生縱向蠕滑力。

除上述的幾種同步轉速的耦合輪對，還有學者提出了兩側車輪可以形成一定轉速差的差速耦合輪對［13］。這種耦合輪對將應用在汽車上的機械差速器應用到耦合輪對上，以實現輪對的兩側車輪在必要時可以差速運行。繼而文獻［14］對比分析了分別裝有機械差速器耦合輪對、傳統輪對和獨立旋轉車輪的軌道車輛在曲線和直線上的導向性能，發現機械差速器耦合輪對也能較好地解決獨立旋轉車輪的導向問題。機械差速器作為左右車輪差速運行的被動控制裝置，結合主動控制系統實現獨立車輪橫向機械差速控制，以使得左右輪對與軌道的接觸均為純滾動，不產生輪軌間輪緣的擠壓與磨耗［15］。

文中根據機械差速器耦合輪對的差速輪對技術原理，提出了一種新型的采用電磁耦合器的耦合輪對—電磁差速耦合輪對。電磁差速耦合輪對是通過電磁耦合器將兩側獨立旋轉車輪通過輪系傳動進行耦聯，且兩側車輪轉速差是可控的。

1 電磁差速耦合輪對的導向機理

電磁差速耦合輪對的結構如圖1所示，其由左右側車輪、軸橋、電磁耦合器和齒輪傳動構成。

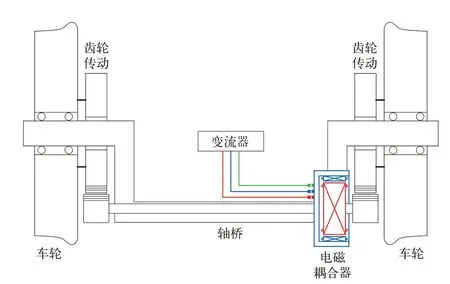
圖1 電磁差速耦合輪對結構示意圖

1.1 電磁耦合器原理

電磁差速耦合輪對為實現兩側車輪轉動耦合且轉速差可控，文中對電磁耦合器的結構進行了設計。電磁耦合器的結構如圖2所示，即1臺定子可以旋轉的交流感應電機，旋轉的定子稱為外轉子，轉子稱為內轉子。內外轉子通過齒輪傳動分別與兩側車輪連接形成機械傳動通路，實現將兩側車輪轉動耦合；外轉子上設三相繞組通過集電環和電刷與變流器形成電氣通路，利用變流器控制輸出電流以控制內外轉子間轉速差。

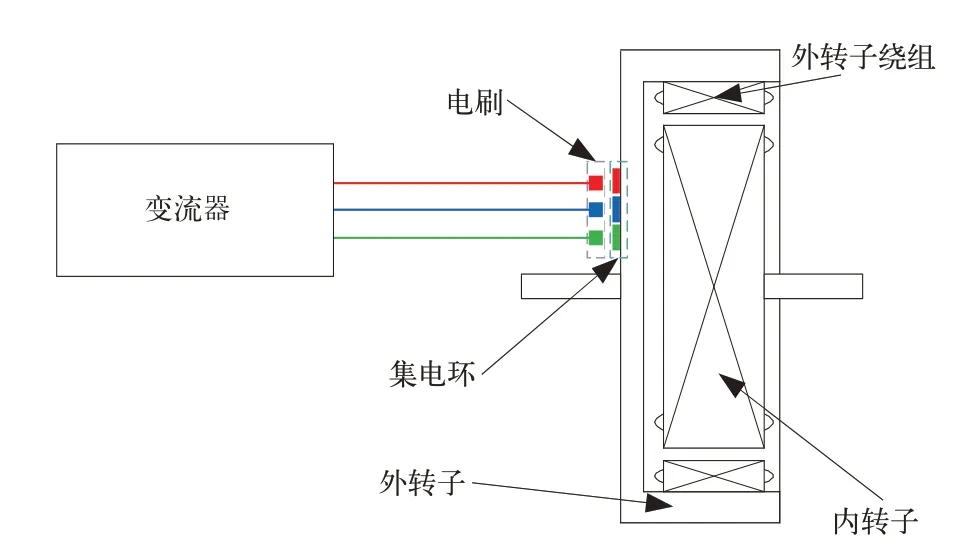
圖2 電磁耦合器結構示意圖

由于電磁耦合器是從籠式異步電機演化而來的，因此分析電磁耦合器的特性，最有效的方法就是等效電路法［16］。仿照異步電機的等效電路分析方法，根據歸算前后保證電磁耦合器的通電端口的電磁性質不發生改變的歸算原則，繞組的歸算關系為式（1）［17］：

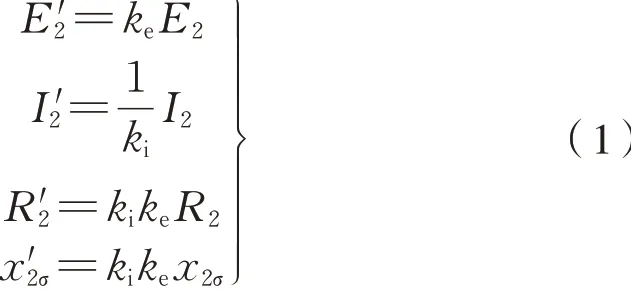
式中：E2，E′2為歸算前后的內轉子繞組電勢；I2，I′2為歸算前后的內轉子繞組電流；R2，R′2為歸算前后的內轉子繞組電阻；x2σ，x′2σ為歸算前后的內轉子繞組漏電感；ke為電勢歸算系數，且為電流歸算系數，且其中m1，m2為內外轉子繞組相數，N1kw1，N2kw2為內外轉子的有效匝數。根據以上歸算后，則電磁耦合器的T型等效電路如圖3所示［18］。

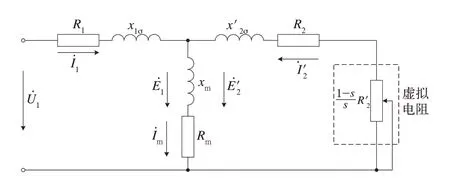
圖3 電磁耦合器的T型等效電路[19]

在歸算過程中，由于將內轉子等效為相對于外轉子的靜止轉子，故出現了如圖3中所示的虛擬電阻從而有虛擬電阻的電功率即是電磁耦合器內外轉子間通過氣隙磁場傳遞的機械功率，該功率Pe為式（2）：

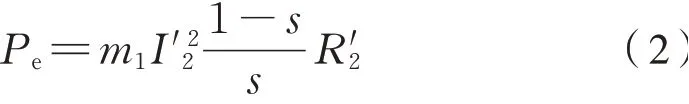
式中：s為電磁耦合器的轉差率，其表達式為式（3）：

式中：ω為外轉子繞組通電角頻率；ωi為內轉子轉動角頻率；ωo為外轉子轉動角頻率。

根據式（2）分析電磁耦合器能量轉化關系，若Pe為負值則表示虛擬電阻作為等效電路中的電源，吸收耦合輪對系統的機械能轉化成電能。若Pe為正值則表示虛擬電阻在等效電路中為用電器，可以將電能轉化為電磁差速耦合輪對系統的機械能。根據式（2）、式（3）可以得到電磁耦合器所傳遞的轉矩Te為式（4）：

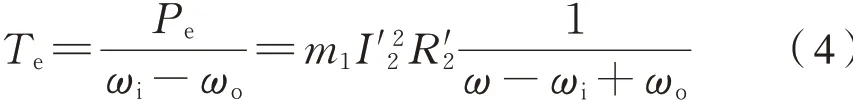
1.2 電磁耦合輪對導向機理分析

電磁耦合器內外轉子間的電磁力矩是將輪對的兩側車輪旋轉運動耦合起來的關鍵。文中利用電磁耦合器內外轉子間的電磁力矩和電磁差速耦合輪對的縱向蠕滑力之間的關系，分析電磁差速耦合輪對在主動控制系統作用下的導向機理。為獲得這兩者間的關系，對電磁耦合輪對進行受力分析，如圖4所示。圖4中坐標系為右手坐標系，且x軸正方向為輪對前進方向。

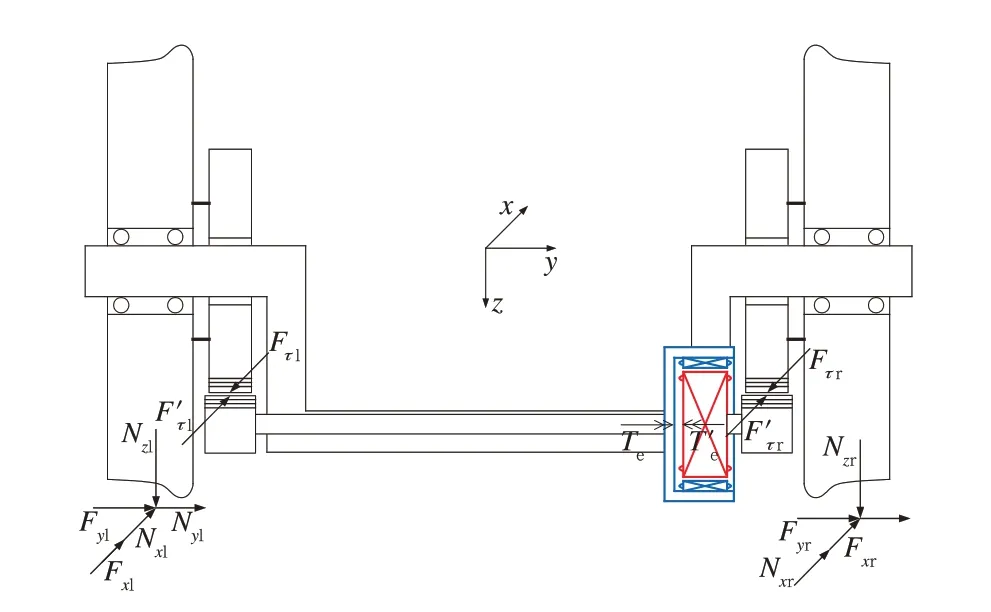
圖4 電磁差速耦合輪對受力圖

左側車輪穩態的點頭運動為式（5）：

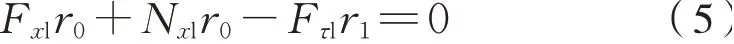
內轉子穩態的旋轉運動為式（6）：

右側車輪穩態的點頭運動為式（7）：

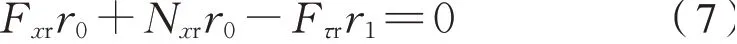
外轉子穩態的旋轉運動為式（8）：

式（5）~式（8）中：F xl，F xr分別為左右側車輪縱向蠕滑力；N xl，N xr分別為左右側輪軌法向力在縱向的分量；Te，T′e為電磁力矩，且Te=T′e；Fτl，F′τl，Fτr，F′τr為齒輪嚙合圓周力，Fτl和F′τl互為反作用力，Fτr和F′τr互為反作用力；r0為名義滾動圓半徑；r1，r2為齒輪節圓半徑；i=r1/r2為齒輪傳動比。

分別將式（6）代入式（5）、式（8）代入式（7）可得式（9）：

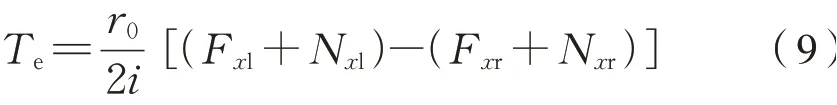
設縱向蠕滑力矩為M=(F xl-F xr)b，其中b為名義滾動圓橫向跨距之半。且在輪對正常運行時，接觸點不會偏移車輪踏面最低點很多，故左右側輪軌法向力在縱向的分量可忽略不計，則有式（10）：

進一步將式（4）代入式（10）中可得式（11）：

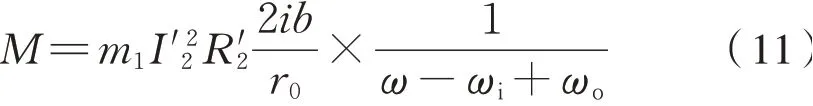
根據式（2）和式（11）分析電磁差速耦合輪對在直線線路和曲線線路2種工況下不同運行狀態的導向機理。

直線線路運行工況：

（1）當ωi>ωo時，即電磁差速耦合輪對的外側車輪轉速大于內側車輪轉速，輪對會形成正的搖頭角從而偏離軌道中心向軌道內側運動。若使得外轉子繞組通電角頻率ω近似為零，則輪對的縱向蠕滑力矩M的值為負值，輪對在負的縱向蠕滑力矩下形成負的搖頭角向著軌道中心運動。另外，電磁耦合器的耦合功率Pe為正值，故電磁耦合器在消耗電磁差速耦合輪對的機械能，使得兩側車輪轉速趨同。進一步驗證了電磁耦合輪對擁有了像傳統剛性輪對那樣的直線對中能力。

（2）當ωi<ωo時，即電磁差速耦合輪對的外側車輪轉速小于內側車輪轉速，輪對會形成負的搖頭角從而偏離軌道中心向軌道外側運動。但輪對的縱向蠕滑力矩M的值為正值，輪對會形成正的搖頭角恢復到線路中心運行。

曲線線路運行工況：

（1）當ω>ωi-ωo時，即外轉子通電角頻率控制期望ω未達到電磁耦合器內外轉子間轉速差控制期望。縱向蠕滑力矩M的值為正值，則輪對形成正的搖頭角，從而使得輪對以趨向于軌道徑向位置的姿態通過曲線。同時，電磁耦合器傳遞的機械功率Pe為正值，可見電磁耦合器將電能轉化為驅動內外轉子間形成轉動差的機械能，繼而使輪對順利通過曲線。

（2）當ω<ωi-ωo時，即電磁耦合器內外轉子間轉速差大于控制期望。輪對的縱向蠕滑力矩M的值為負，則輪對搖頭角在縱向蠕滑力矩的作用下不斷減小直至回到輪對徑向位置。且耦合器傳遞的電磁耦合功率Pe為負值，說明電磁耦合器作為電路中的電源，將形成內外轉子轉速差的機械能轉化為電磁耦合器電路回路中的電能。

2 電磁耦合輪對仿真分析

文中研究電磁耦合輪對的導向能力，在Simpack多體動力學仿真分析軟件中分別建立與電磁耦合輪對軌道車輛模型和除輪對形式外其他參數均相同的獨立旋轉輪對車輛模型。主要動力學參數見表1。

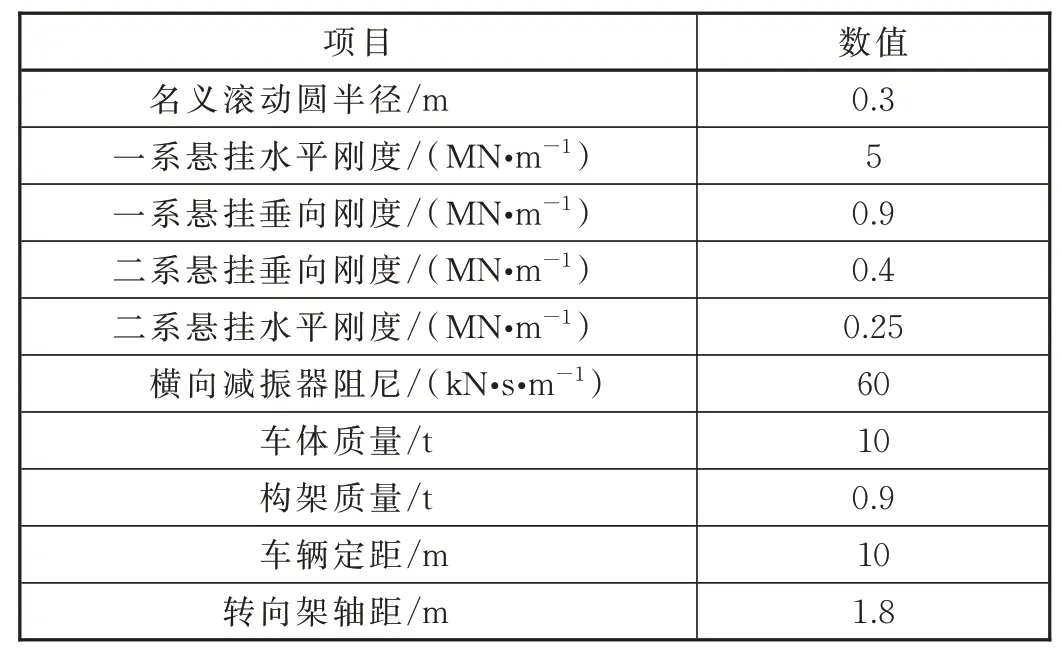
表1 主要動力學參數

2.1 直線對中能力

如果輪對偏離其線路的中心位置，其橫移量若能夠在較短的時間內收斂到0，則說明其具有較好的直線自動對中能力。設置車輛直線行駛速度為72 km/h，且初始橫移量為4 mm［18］，對比獨立旋轉車輪、電磁耦合輪對的直線自動對中能力。

一位輪對橫移量的仿真結果如圖5所示，電磁差速耦合輪對的橫移量在開始的0.2 s內快速接近0，經過一段時間后在0附近小幅振蕩，輪對回到軌道中心，表明輪對具有很好的直線自動對中能力，而獨立旋轉車輪的輪對橫移量緩慢的接近于0。這是因為電磁差速耦合輪對的兩側車輪的點頭運動相互耦合。當兩側車輪轉速不相等時，耦合器會產生耦合力矩，相應地輪軌接觸處會產生縱向蠕滑力以平衡耦合器的耦合力矩。輪對從而在縱向蠕滑力矩的作用下趨向軌道中心運動，而獨立旋轉輪對理論上不存在縱向蠕滑力，因此趨近軌道中心的速度很慢。

圖5 一位輪對橫移量對比

2.2 曲線通過能力

衡量機車車輛曲線通過性能的幾個重要指標是輪軌沖角、輪軌橫向力和脫軌系數［20］。文中設定曲線半徑為100 m，車輛運行速度為36 km/h［18］。選取一位輪對在通過曲線時的時域響應進行對比分析，如圖6所示。

圖6（a）為輪對的兩側車輪轉速差，圖6（b）為輪對在通過曲線時的輪對橫移量。結合圖6（a）和圖6（b）可以看出獨立旋轉車輪在剛進入緩和曲線（一位輪對運行至14 m左右位置）時，其輪對橫移量迅速達到10 mm，即此時發生了輪緣貼靠鋼軌，外側車輪的滾動圓半徑增加顯著而內側車輪的滾動圓半徑減小，故產生了較大的轉速差波動。

另外，根據差速型輪對以曲線徑向位置的姿態通過曲線時，外側車輪前進速度為內側車輪前進速度為可得在通過圓曲線時，左右車輪轉速差期望值為式（12）：

式中：b為滾動圓橫向跨距之半；v為輪對質心前進速度；R為圓曲線軌道中心線半徑；r0為名義滾動圓半徑。將仿真條件代入式（12）計算得到左右車輪轉速差期望值為0.498 rad/s。圖6（a）顯示獨立旋轉車輪的兩側車輪轉速差通過曲線線路過程中始終都未達到轉速差期望值，外側車輪則會滯后于內側車輪。

圖6（c）為一位輪對的輪軌沖角仿真結果，其表明電磁耦合輪對的輪軌沖角較于其他2種輪對小，可以認為電磁差速耦合輪對以趨近線路徑向的姿態通過曲線。這是因為獨立旋轉車輪的外側車輪在沿線路方向上的位置存在著一定程度滯后于內側車輪，故形成了較大的輪軌沖角。

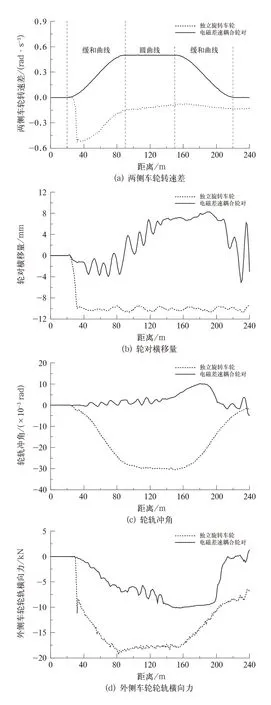
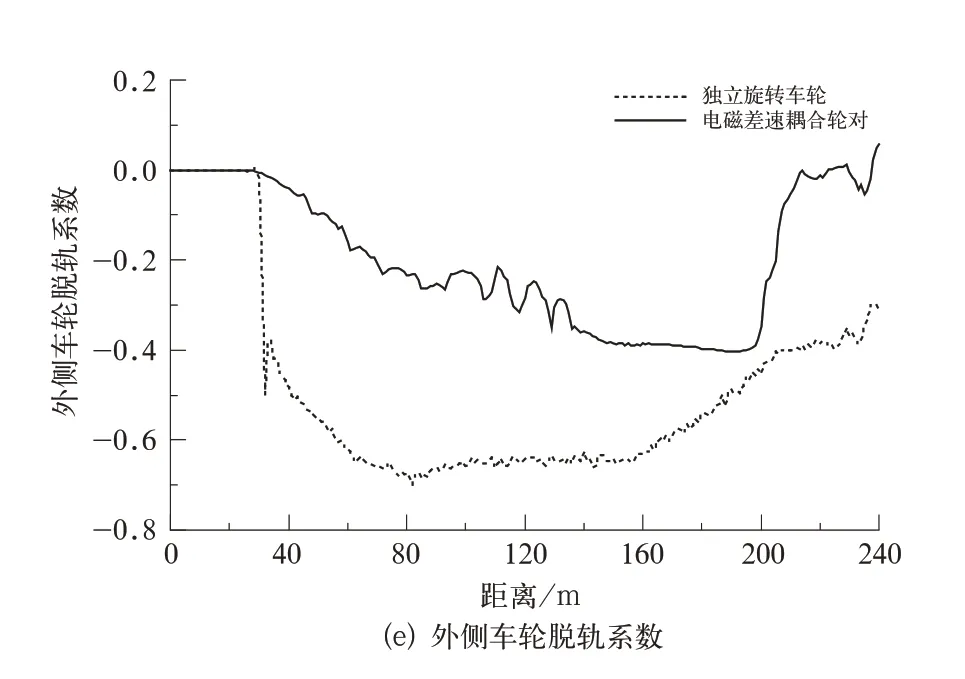
圖6 通過曲線時一位輪對的時域響應

圖6（d）和圖6（e）分別為一位輪對外側車輪的輪軌橫向力和脫軌系數，其顯示了電磁差速耦合輪對在圓曲線（90~150 m路段）上運行過程中，其外側輪軌橫向力相較于其他2種輪對低了44%，外側車輪脫軌系數低了近39%。綜上所述，電磁差速耦合輪對在通過小半徑曲線時，具有很好的安全性能。

由于輪對在小半徑曲線時，會出現輪緣區與鋼軌接觸，輪緣區域內的等效接觸角較大，故自旋蠕滑的現象較為突出，在計算輪軌磨耗功率時增加考慮了自旋蠕滑。通過根據文獻［21］給出的輪軌接觸處的磨耗功率P為式（13）：

式中：Fx，Fy，T z分別為縱向蠕滑力、橫向蠕滑力和自旋蠕滑力矩，ξx，ξy，ξs分別為縱向蠕滑率、橫向蠕滑率和自旋蠕滑率，其輪軌的蠕滑率/力（矩）仿真結果結果如圖7所示。

圖7（a）、圖7（b）、圖7（c）分別為一位輪對外側車輪的輪軌橫向、縱向和自旋蠕滑率/力（矩）。由于電磁差速耦合輪對的輪軌沖角明顯小于其他2種輪對形式的，致使電磁差速耦合輪對的橫向蠕滑率也明顯小于獨立旋轉車輪的橫向蠕滑率。另外，電磁差速耦合輪對是可以主動差速，兩側車輪的轉速在通過曲線時則可以形成一定的差值，這一差值可以彌補輪對兩側車輪在相同時間內需要走過距離的差值，因此其縱向蠕滑率也相對較小。圖7（c）顯示出獨立旋轉車輪的自旋蠕滑率明顯大于電磁差速耦合輪對，這是因為獨立旋轉車輪在通過曲線時，輪緣始終貼靠鋼軌運行，這使得自旋蠕滑率較大。

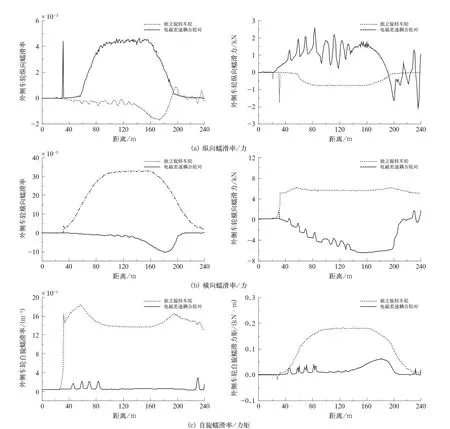
圖7 一位輪對外側車輪蠕滑率/力（矩）

根據式（13）計算獨立旋轉車輪和電磁差速耦合輪對的外側車輪輪軌磨耗功率，結果如圖8所示。由圖8可見電磁差速耦合輪對的磨耗功率在通過曲線時明顯低于獨立旋轉車輪。綜上所述，電磁差速耦合輪對可以較好地解決獨立旋轉車輪曲線通過能力不足的問題。

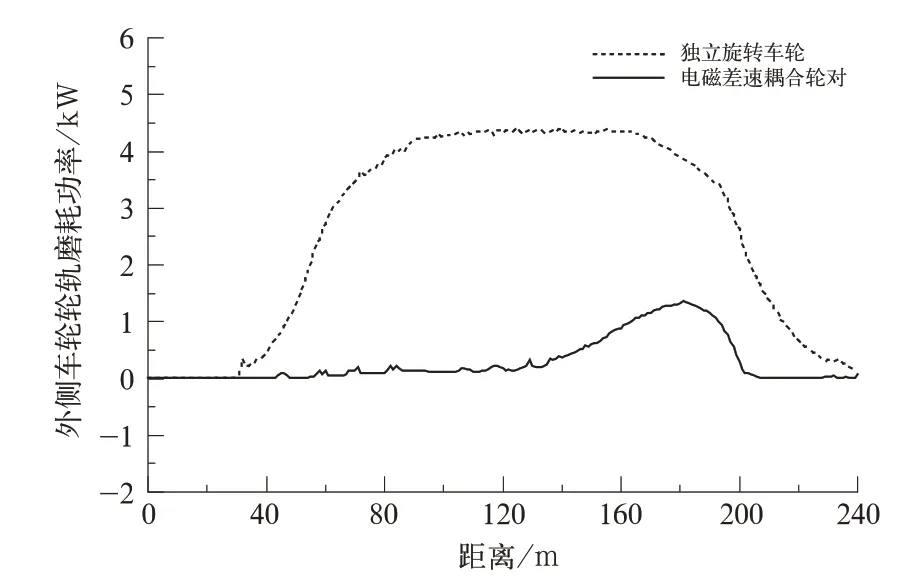
圖8 一位輪對外側車輪磨耗功率

3 結論

研究的結論如下：

（1）針對獨立旋轉車輪存在導向性能不足的問題，文中提出了在獨立旋轉車輪基礎上橫向加裝電磁耦合器的耦合輪對結構方案。

（2）電磁差速耦合輪對的導向機理：在直線線路運行時，若使得電磁耦合器內外轉子間的轉速趨于同步，電磁差速耦合輪對的縱向蠕滑力矩會抑制輪對形成搖頭角，以使輪對趨近軌道中心運行。在曲線線路運行時，若電磁耦合器內外轉子間的轉速差小于期望值，電磁耦合器的耦合功率為正值，可以迫使輪對兩側車輪形成轉速差，從而使輪對以趨近曲線線路徑向位置的姿態通過曲線。若電磁耦合器內外轉子間的轉速差大于期望值，輪對搖頭角在負的縱向蠕滑力矩作用下不斷減小直至回到輪對徑向位置。

（3）通過對獨立旋轉車輪和電磁差速耦合輪對的仿真結果對比分析發現：電磁差速耦合輪對的直線自動對中能力和曲線通過時安全性能和輪軌磨耗性能均優于獨立旋轉車輪，說明了電磁差速耦合輪對可以解決獨立旋轉車輪的直線自動對中能力和曲線通過能力不足等問題。

（4）結合工程實際，研究電磁耦合器本身的結構設計及空間布置，同時，關注運用環境下電磁耦合輪對的安全可靠性等問題。