Manipulating vector solitons with super-sech pulse shapes
Yan Zhou(周延) Keyun Zhang(張克赟) Chun Luo(羅純) Xiaoyan Lin(林曉艷)Meisong Liao(廖梅松) Guoying Zhao(趙國營) and Yongzheng Fang(房永征)
1School of Science,Shanghai Institute of Technology,Shanghai 201418,China
2Key Laboratory of Materials for High Power Laser,Shanghai Institute of Optics and Fine Mechanics,Chinese Academy of Sciences,Shanghai 201800,China
3School of Materials Science and Engineering,Shanghai Institute of Technology,Shanghai 201418,China
Keywords: vector soliton,super-sech,central wavelength,manipulation,optical fiber
1. Introduction
The research about optical solitons is always a hot topic in recent decades. Optical soliton can be considered as a kind of ultra-short optical pulse that maintains its temporal waveform in nonlinear medium under appropriate constrained conditions.[1–5]Optical soliton is often studied in passively mode-locked fiber laser with compact structure, because of the controllable dispersion and nonlinearity in optical fiber cavity.[6–10]Until now, there have been many reports about femtosecond fiber lasers in normal and anomalous dispersion regimes. In these fiber lasers, nanomaterial based saturable absorber is often adopted to achieve stable mode-locking. All fiber saturable absorber that combines single-mode fiber and graded index multimode fiber has been proved to have good modulation property because of the nonlinear multimode interference in mode-locked fiber laser. Besides,there are some other techniques that can generate mode-locked pulses, such as nonlinear polarization rotation, nonlinear amplified loop mirror and nonlinear optical loop mirror. Recently, the soliton dynamics in fiber lasers have also been investigated experimentally and theoretically. For instance, soliton molecules have been observed in real time,[11]the transition dynamics fromQ-switching to mode-locking has been reported,[12]and the entire buildup process of harmonic mode-locking has been revealed firstly in Ref.[13]. The soliton with super-sech pulse shape has also been theoretically analyzed,[14]but the generation of super-sech optical soliton in fiber laser has seldom been reported. The study about super-sech optical soliton is meaningful to the fields of optical communications, fiber sensing and fiber laser.
Generally,the single-mode fiber(such as SMF-28,SMF-28e and HI 1060)used in the laser cavity is slightly anisotropic because of the fabrication imperfection, which can produce weak intra-cavity intrinsic linear birefringence. Combining intrinsic birefringence and externally imposed birefringence, output laser pulse can have two electric components in orthogonal polarization directions, meaning vector soliton (VS) is achieved in this condition. The externally imposed birefringence can be tuned by using polarization controller(PC)or introducing a piece of polarization-maintained optical fiber. The generated VS can be polarization-locked,group-velocity-locked or polarization-rotated,which is dependent on the strength of linear birefringence and linear birefringence induced cross-phase modulation between orthogonal polarization modes.[15–17]The generation and dynamics of fiber VSs have been reported by many research groups. Also,the manipulation of VSs out of laser cavity has been theoretically and experimentally studied. For example, Zhaoet al.reported the numerical simulations about the generation of pseudo-high-order group-velocity-locked VSs.[18]Zhaoet al.also demonstrated their experimental results in their later work.[19]We theoretically investigated the out-cavity manipulation of Yb-doped fiber laser VSs with various pulse properties, which include super-Gaussian pulses,[20]dark–dark pulses,[21]bright–dark pulses,[22]self-similar pulses,[23]selfsimilar vector bisolitons,[24]and so on.[25–28]Through varying soliton pulse parameters in orthogonal directions, finally,various kinds of pulse shapes and optical spectra in output orthogonal directions were got. But there have been few reports about super-sech VS pulses’ modulation. In this manuscript, we simulate the out-cavity modulation of supersech VS pulses at or near 1064 nm wavelength position,when it is polarization-locked or group-velocity-locked. Through the change of pulse parameters in orthogonal polarization directions,various kinds of VSs are shown after the polarization splitting. Our simulations are useful for relevant theoretical and experimental studies about super-sech VS.
2. Optical fiber system description

Fig.1. Optical fiber system.
The optical fiber system used in our simulation is demonstrated in Fig. 1, and this theoretical model has been used in some previous papers.Figure 1 shows that input vector soliton from 1064 nm ultrafast fiber laser with electric amplitudes ofA1andA2in orthogonal directions enters into the optical fiber system,and is manipulated through the change of four soliton pulse parameters,including amplitude ratio(A2/A1),time delay(ΔT)between orthogonal components,linear birefringence(or phase difference)that is imposed by PC,and projection angle(θ)that can be varied by rotating polarization beam splitter(PBS). SMF is single-mode fiber, and Col is optical collimator which can align the output vector soliton pulses. We can see during the manipulation, the principal and minor axes of the elliptically polarized laser beam are rotated, and the amplitudes in these two orthogonal polarization directions also vary under appropriate conditions. In this optical fiber system,the polarization of VS can be controlled through the variations of amplitude ratio, time delay and phase difference. And the energy of manipulated VS is separated through changing projection angle.

In Eq. (3),Ax(t) andAy(t) are respectively the complex amplitudes in horizontal and vertical directions after polarization splitting by PBS,andθis projection angle. After polarization splitting, the temporal intensities in output orthogonal directions are

In Eq.(4),Ii(t)represents the output pulse shape’s intensity in horizontal or vertical direction wheniisxory.And the optical spectra of orthogonal modes can be calculated according to
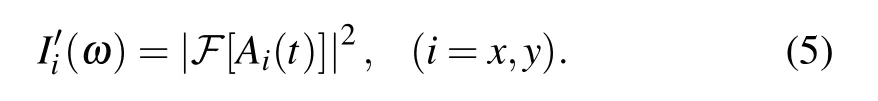
In Eq. (5),I′i(ω) is optical spectrum’s intensity in horizontal or vertical direction wheniisxory,ωis angular frequency,andF[]represents Fourier transform.
Indeed, the VS evolution in optical fiber system can be numerically solved by using coupled nonlinear Schr¨odinger equations(NLSEs). In our simulation,we simplify the model by assuming the net effects of different pulse parameters. This assumption has already been reported in Ref.[19],and the experimental results agreed with the theory. In this approximation, the length of SMF in the model is assumed to be much shorter than dispersion length(T20/|β2|)and nonlinear length(1/(γP0)),which neglect the influence of dispersion and nonlinearity on pulse shapes and optical spectra. This approximation can be achieved through the control of pulse width(T0),group-velocity dispersion(β2)and pulse peak power(P0).γis fiber nonlinearity and depends on the type of SMF. Of course,if the fiber length is comparable or larger than dispersion/nonlinear length, the coupled NLSEs must be employed and soliton pulses in orthogonal polarizations will breathe in time/frequency domain.
3. Simulation
In this section, we conduct the simulation about manipulating super-sech VSs. Firstly, we assume input orthogonal components own the same central wavelength (λ1=λ2=1064 nm)and simulate the manipulation(see Figs.2–5).Secondly, input orthogonal components are assumed to have different central wavelengths(λ1=1063 nm,λ2=1065 nm),and the results are concluded from Figs.6–9.
Figure 2 gives theoretical simulation results whenA2/A1is 1/1.5, 1/1.3, 1/1, 1.3/1, 1.5/1, andθ=0°, ΔT=0.5 ps,Δφ=π/2.T1=T2=5 ps,which is the same for all the cases in this manuscript. The input orthogonal modes’ phase difference isπ/2 when polarization is locked, and in this situation the net phase difference is alsoπ/2, so the summation of externally imposed linear birefringence and intrinsic linear birefringence is zero. Figures 2(a)–2(e) show that the output pulse peak intensities in horizontal and vertical directions have consistent variation trend as the change of amplitude ratioA2/A1,because of the energy exchange whenθ=0°. The pulse shapes in orthogonally polarized directions are slightly mismatched and will be overlapped totally when ΔT=0 ps.In corresponding optical spectra of Figs.2(f)–2(j),both orthogonally polarized optical spectra have trapezoid like optical spectrum shapes,which means the optical spectrum peak position has a flat region, because of the temporal sharp pulse peak.Also,the optical spectra in orthogonal directions will coincide with each other whenA2/A1=1/1,although ΔT/=0 ps in this situation.
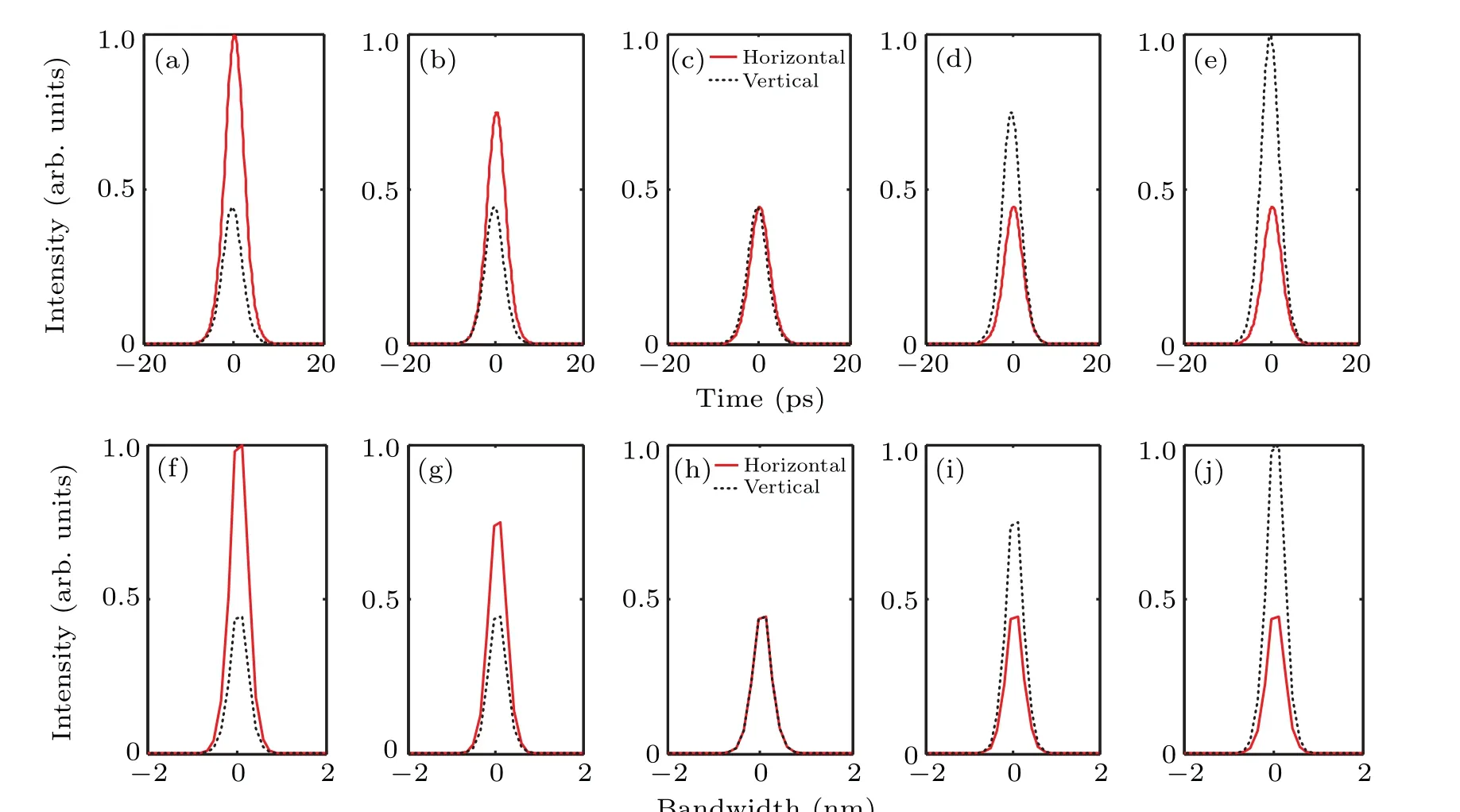
Fig.2. Simulation results of orthogonal modes when A2/A1 is changed(λ1=λ2): (a)–(e)waveforms,(f)–(j)corresponding spectra.
Figure 3 gives theoretical simulation results whenθis 10°, 25°, 40°, 55°, 70°, andA2/A1=1, ΔT=1.5 ps, Δφ=π/2. The time delay of orthogonally polarized pulse shapes in Figs.3(a)–3(e)will be changed as the increase ofθ. The variation trend is that the time delay in orthogonal directions will decrease whenθapproaches to 45°,and the time delay is zero whenθ=45°. In optical spectra of Figs.3(f)–3(j),the central wavelength difference has contrary variation trend compared with time delay of orthogonal components. From this figure,it is concluded that through changing projection angle,the energy distribution in horizontal and vertical directions will be varied,which will induce the changes of phase velocities(time delay)and group velocities(central wavelengths)of output orthogonal components.
Figure 4 gives theoretical simulation results when ΔTis 2 ps, 4 ps, 6 ps, 8 ps, 10 ps, andA2/A1= 1,θ= 40°,Δφ=π/2. Figures 4(a)–4(e)demonstrate that the pulse peak intensities in orthogonal directions will decrease when ΔTincreases from 2 ps to 6 ps, and then remain stable when ΔTincreases from 6 ps to 10 ps. We can see there are obvious two pulse peaks in both horizontal and vertical directions when ΔTis 6 ps, 8 ps and 10 ps, which means “2+2” pseudo-highorder VSs with group-velocity-locked are generated. They are called “pseudo-high-order” rather than “high-order” because the phases of orthogonal pulses are not locked in this situation.The occurrence of two pulses in horizontal/vertical direction is due to the interferences in orthogonal directions. Figures 4(f)–4(j) demonstrate the simulated optical spectra, showing that the peak intensities increase with increased ΔT. Orthogonal modes have slightly different central wavelengths, meaning group velocities are changed when ΔTincreases. Besides,another pedestal that at shorter(or longer)wavelength position in horizontal(or vertical)direction will appear when ΔTreaches 6 ps,and peak intensity of the pedestal will also increase with increased ΔT.
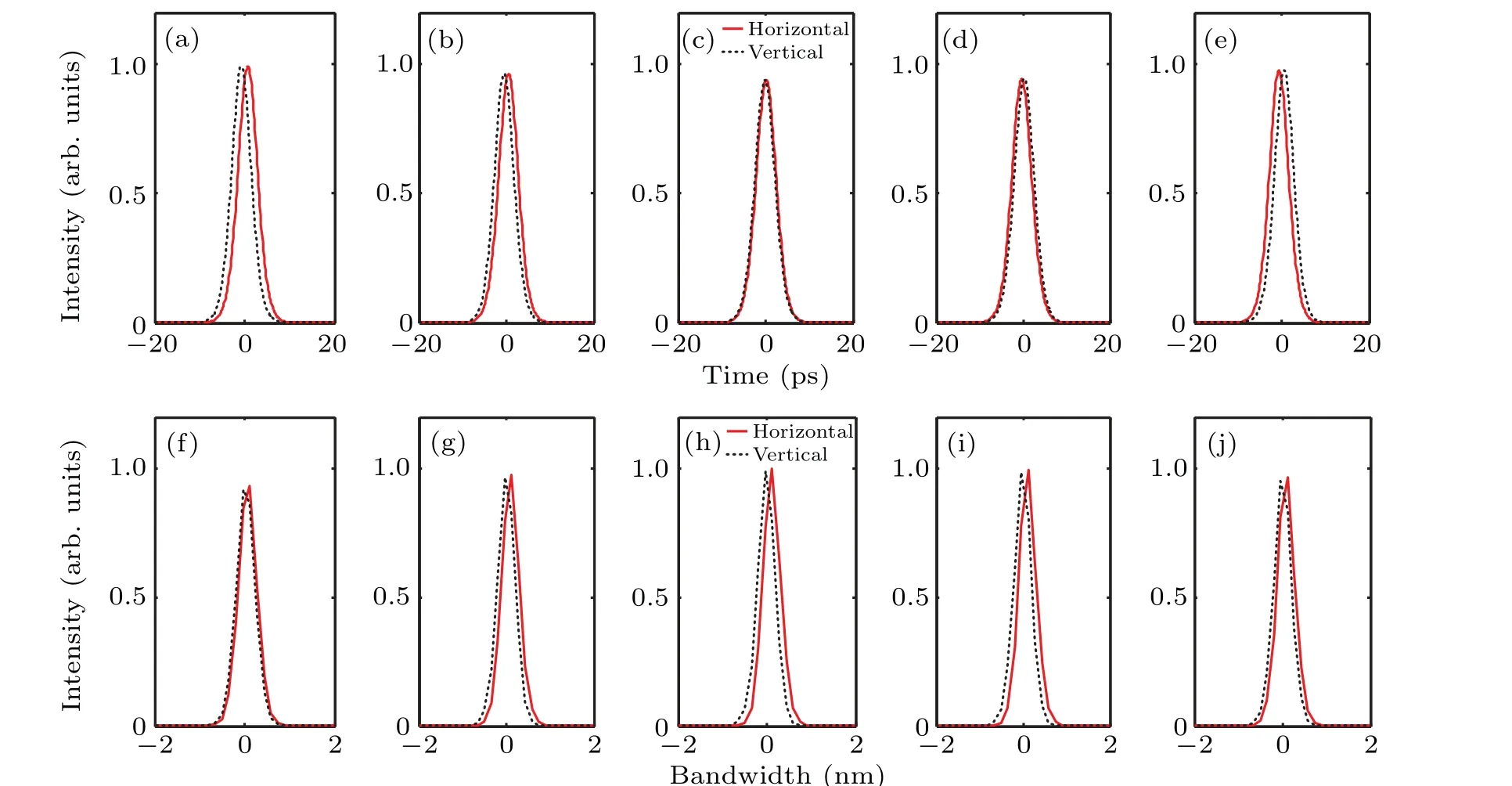
Fig.3. Simulation results of orthogonal modes when θ is changed(λ1=λ2): (a)–(e)waveforms,(f)–(j)corresponding spectra.
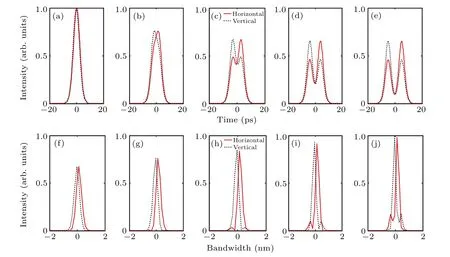
Fig.4. Simulation results of orthogonal modes when ΔT is changed(λ1=λ2): (a)–(e)waveforms,(f)–(j)corresponding spectra.
At last,we change Δφand Fig.5 gives theoretical simulation results when Δφisπ/7,2π/7,3π/7,4π/7,5π/7,andA2/A1=1,θ=45°, ΔT=0 ps. Pulse shapes in Figs. 5(a)–5(e) and optical spectra in Figs. 5(f)–5(j) demonstrate similar variation trend as the increase of Δφ. In other words,the peak intensities of pulse shapes and corresponding optical spectra in horizontal/vertical polarization direction will decrease/increase with increased Δφ. The peak intensities of pulse shapes/optical spectra in orthogonal directions are always different under symmetry projection, which means the change of phase difference can induce energy flow between orthogonal directions.
Figure 6 gives theoretical simulation results whenA2/A1is 1/1.5, 1/1.3, 1/1, 1.3/1, 1.5/1, andθ=0°, ΔT=0.5 ps,Δφ=0.The peak intensity variation trend in Figs.6(a)–6(e)is almost the same to Figs.2(a)–2(e),regardless of different Δφvalues. The optical spectra in Figs.6(f)–6(j)show that the optical spectrum peak intensity of horizontal/vertical mode has the same variation trend to the change ofA2/A1. The horizontal(or vertical)mode is always at shorter(or longer)wavelength position regardless of the variation of peak intensity.The unchanged output central wavelengths indicate that the group velocities of orthogonal modes are robust to the change of amplitude ratio.

Fig.5. Simulation results of orthogonal modes when Δφ is changed(λ1=λ2): (a)–(e)waveforms,(f)–(j)corresponding spectra.
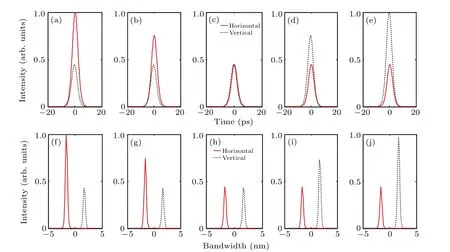
Fig.6. Simulation results of orthogonal modes when A2/A1 is changed(λ1/=λ2): (a)–(e)waveforms,(f)–(j)corresponding spectra.
Figure 7 demonstrates the simulation results whenθis 10°,25°,40°,55°,70°,andA2/A1=1,ΔT=1.5 ps,Δφ=0.Comparing Figs. 7(a)–7(e) and 3(a)–3(e), it is obvious that pulse splitting occurs for the case of different central wavelengths whenθis changed. The generation of multiple peaks is due to the enhanced interference in horizontal/vertical direction whenθ/=0°and with different input central wavelengths. Also,the maximum pulse peak intensities of orthogonal modes vary with differentθvalues. The temporal peak intensity and oscillation depth of horizontal/vertical mode will reach the maximum whenθ=45°(not depicted in Fig.7). In Figs.7(f)–7(j),there are two peaks for both output modes.The peak intensity of shorter wavelength of horizontal(or vertical)mode will decrease(or increase)with increasedθ,which will induce the increased (or decreased) peak intensity of longer wavelength of horizontal (or vertical) mode. The reason of generating dual-wavelength VS is that the change of projection angle will induce the intensity redistribution in two wavelengths with fixed total energy. It should be noted that the orthogonal optical spectra are overlapped but corresponding pulse shapes are not whenθ=45°.
Figure 8 gives theoretical simulation results when ΔTis 2 ps, 4 ps, 6 ps, 8 ps, 10 ps, andA2/A1= 1,θ= 40°,Δφ=0. Figures 8(a)–8(e) demonstrate that as the increase of ΔT, the two pulsed waveforms in orthogonally polarized directions start to separate with each other, and their pulse peak intensities decrease with increased ΔT. Also, the pulse shapes will become relatively smooth when they start to separate,because of the decreased interaction between orthogonal components when time delay increases. In the optical spectra described in Figs. 8(f)–8(j), there are two peaks for both orthogonally polarized modes because of non-zeroθvalue. The optical spectrum peak intensity of 1063 nm component in horizontal/vertical direction is always higher/lower than 1065 nm component,and the peak intensities are almost unchanged under the variation of ΔT.
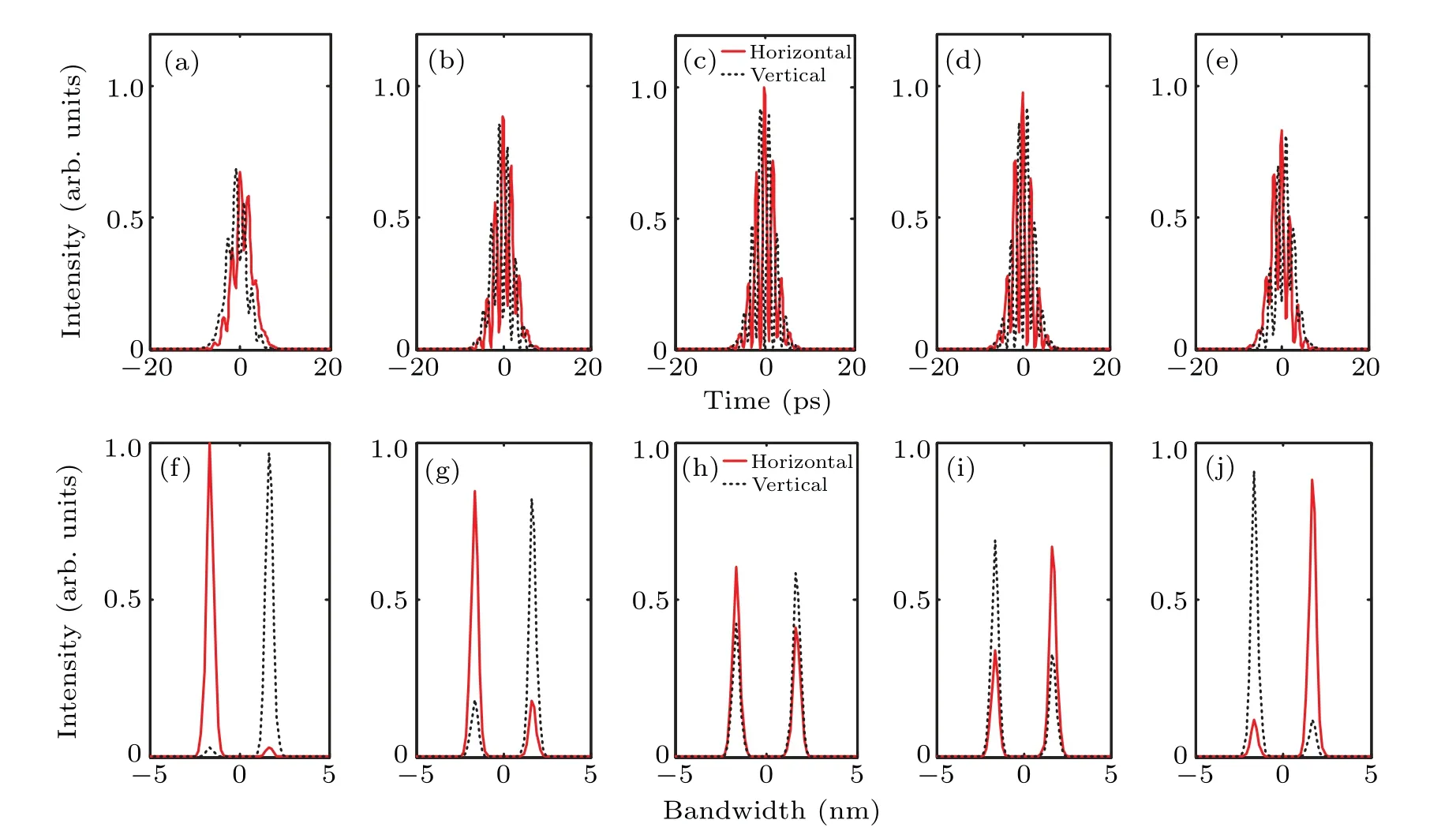
Fig.7. Simulation results of orthogonal modes when θ is changed(λ1/=λ2): (a)–(e)waveforms,(f)–(j)corresponding spectra.
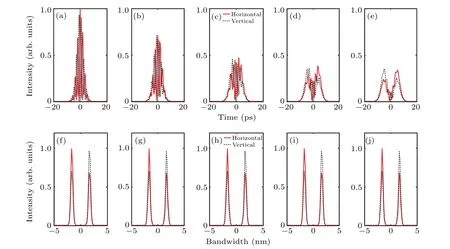
Fig.8. Simulation results of orthogonal modes when ΔT is changed(λ1/=λ2): (a)–(e)waveforms,(f)–(j)corresponding spectra.
At last,Δφis changed and Fig.9 gives theoretical simulation results when Δφisπ/7,2π/7,3π/7,4π/7,5π/7,andA2/A1=1,θ=45°, ΔT=0 ps. In Figs. 9(a)–9(e), pulsed waveforms in orthogonally polarized directions have multiple pulse peaks. The temporal envelopes are almost the same but these peaks are not overlapped even when ΔT=0 ps,because of different phase distributions in orthogonal directions. In Figs. 9(f)–9(j), the optical spectra in horizontal and vertical directions are overlapped because of the symmetry projection.Besides, the dual-wavelength optical spectra at 1063 nm and 1065 nm are unchanged as the increase of Δφ,meaning optical spectra in orthogonal directions are robust to the change of phase difference.
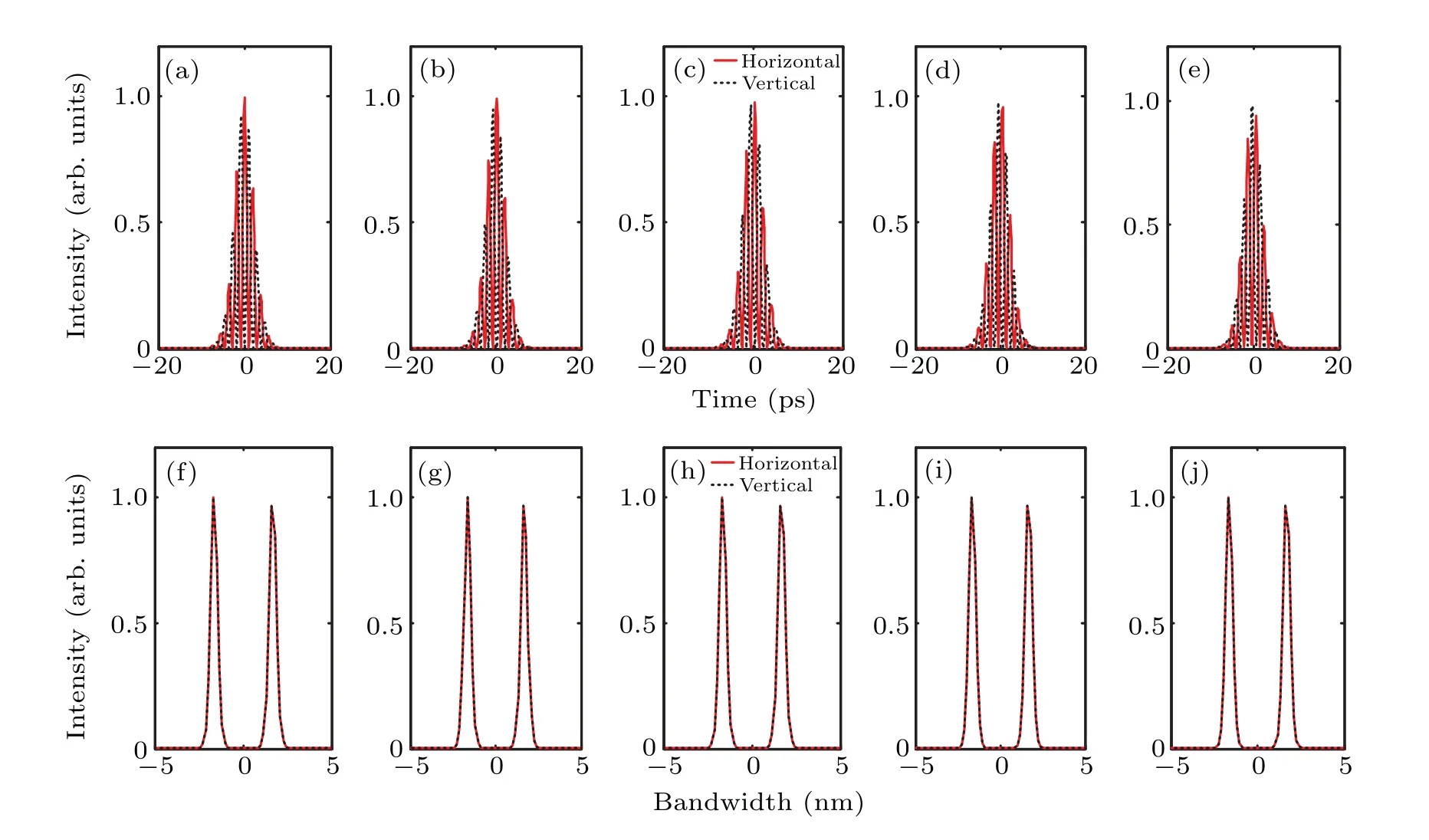
Fig.9. Simulation results of orthogonal modes when Δφ is changed(λ1/=λ2): (a)–(e)waveforms,(f)–(j)corresponding spectra.
4. Conclusion
We gave theoretical simulation results about manipulating super-sech VSs in this work,whether the orthogonal components had same or different input central wavelengths. The output orthogonally polarized pulse shapes and optical spectra were always smooth when input orthogonal modes have the same central wavelength. By comparison, pulse shapes with multiple peaks and dual-wavelength optical spectra in orthogonally polarized directions could be achieved with different central wavelengths. The simulation results explore the supersech vector optical soliton dynamics in optical fiber system,and have applications in the fields of polarization multiplexing and coherent optical detectors in optical communications,through controlling the polarizations of super-sech VSs.
Acknowledgements
Project supported by the National Key Research and Development Program of China(Grant No.2018YFB0504500),the National Natural Science Foundation of China (Grant Nos. 62105208, 51972317, and 61875052), Shanghai Sailing Program (Grant No. 20YF1447500), Special Project for Industrialization of High-tech Science and Technology between Jilin Province and the Chinese Academy of Sciences(Grant No.2021SYHZ0029),and Natural Science Foundation of Shanghai(Grant No.22ZR1470700).
- Chinese Physics B的其它文章
- Erratum to“Boundary layer flow and heat transfer of a Casson fluid past a symmetric porous wedge with surface heat flux”
- Erratum to“Accurate GW0 band gaps and their phonon-induced renormalization in solids”
- A novel method for identifying influential nodes in complex networks based on gravity model
- Voter model on adaptive networks
- A novel car-following model by sharing cooperative information transmission delayed effect under V2X environment and its additional energy consumption
- GeSn(0.524 eV)single-junction thermophotovoltaic cells based on the device transport model

