最小體積和平滑性約束的非負(fù)矩陣分解高光譜解混算法
李登剛 李 潔
(湖南工業(yè)大學(xué) 軌道交通學(xué)院, 湖南 株洲 412007)
0 引言
近年來(lái),衛(wèi)星以及遙感技術(shù)得到了突飛猛進(jìn)的發(fā)展,高光譜圖像因其具有大量的光譜波段數(shù),得到了廣泛的關(guān)注。高光譜圖像目前已經(jīng)廣泛應(yīng)用在了農(nóng)業(yè)監(jiān)督、礦物挖掘、軍事勘測(cè)等領(lǐng)域。但是由于衛(wèi)星成像傳感器空間分辨率的限制,真實(shí)的高光譜圖像場(chǎng)景中往往存在著大量的混合像元。所謂混合像元,是指高光譜圖像中單個(gè)像素包含了多種實(shí)際地物。混合像元的存在,將嚴(yán)重影響和制約后續(xù)對(duì)高光譜圖像的處理與分析。為此,混合像元分解技術(shù)隨之而生。混合像元分解(解混)就是把混合的像元分解為各個(gè)物質(zhì)(稱(chēng)之為端元)及其對(duì)應(yīng)所占的比例(稱(chēng)之為豐度)[1-3]。
近來(lái),關(guān)于混合像元分解的方法層出不窮,總的來(lái)看,可以把這些分解方法分為兩類(lèi)。第一類(lèi),兩步法(two step methods,TSM);第二類(lèi),一步法(single step methods,SSM)。兩步法首先從混合像元中提取出各個(gè)物質(zhì)端元,然后反演計(jì)算出各端元所對(duì)應(yīng)的豐度。常用的端元提取算法有頂點(diǎn)成分分析法[4](vertex component analysis,VCA)、純像素指數(shù)[5](pure pixel index,PPI)、N-FINDR[6]等。提取出端元后,通常通過(guò)全約束的最小二乘法[7](fully constrained least squares,FCLS)來(lái)反演求解出豐度。一步法可以同時(shí)計(jì)算出端元和豐度,傳統(tǒng)的一步法包括獨(dú)立成分分析法[8](independent component analysis,ICA)、最小體積約束的非負(fù)矩陣分解法[9](minimum volume constrained nonnegative matrix factorization,MVCNMF)等。
通過(guò)上述分析可以發(fā)現(xiàn),對(duì)于兩步法,如果在第一步端元提取中存在誤差,那么第二步豐度反演中的累計(jì)誤差將會(huì)繼續(xù)變大。所以,同兩步法相比,一步法可以很好地避免這個(gè)問(wèn)題。此外,在真實(shí)的高光譜圖像中,是否存在純凈像元是未知的。所以,那些需要原始高光譜圖像中存在純凈像元的算法比如VCA、N-FINDR等并不適用。為了解決上述問(wèn)題,混合像元盲分解問(wèn)題隨之而出。所謂盲分解,是指原始高光譜圖像中,是否存在純凈像元,以及端元的個(gè)數(shù)都是未知的。非負(fù)矩陣分解(nonnegative matrix factorization,NMF)最初應(yīng)用在數(shù)據(jù)降維,近年來(lái)被推廣應(yīng)用到了高光譜圖像解混等領(lǐng)域。MVCNMF利用了混合像元的幾何特征,將混合像元構(gòu)成單形體的體積作為約束項(xiàng)加入到了目標(biāo)函數(shù)的罰函數(shù)中。然而這一方法僅考慮了端元的物理屬性,忽略了豐度相關(guān)特性。平滑性約束很好地利用了豐度向量之間的一致性[10],成功地利用了豐度的特征,將豐度的平滑性約束作為罰函數(shù)添加到目標(biāo)函數(shù)中。然而,該方法忽略了端元相關(guān)的物理屬性。
本文利用了高光譜圖像端元和豐度的相關(guān)物理屬性。首先,根據(jù)端元的幾何特征,將混合像元中端元所構(gòu)成單形體的體積作為約束項(xiàng)添加到了目標(biāo)函數(shù)中。其次,充分利用了豐度的平滑性,通過(guò)構(gòu)造平滑性約束項(xiàng),將該約束項(xiàng)也加入到了目標(biāo)函數(shù)中。與傳統(tǒng)方法相比,本文既考慮到了端元的特性,同時(shí)又考慮到了豐度的相關(guān)物理屬性。通過(guò)在非負(fù)矩陣分解的目標(biāo)函數(shù)中結(jié)合體積約束和平滑性約束,提高了混合像元分解的分解精度等問(wèn)題。
1 高光譜圖像解混與非負(fù)矩陣分解
1.1線(xiàn)性混合模型
線(xiàn)性混合模型(linear mixed model,LMM)目前廣泛應(yīng)用在高光譜圖像混合像元分解中[9-10],其數(shù)學(xué)模型定義為
X=AS+N
(1)
式中,矩陣X∈Rn×m表示傳感器觀(guān)測(cè)到的高光譜圖像;矩陣A∈Rn×l表示端元;矩陣S∈Rl×m表示端元所對(duì)應(yīng)的豐度;N表示可能出現(xiàn)的噪聲和誤差。
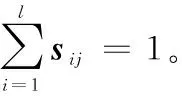
1.2 非負(fù)矩陣分解
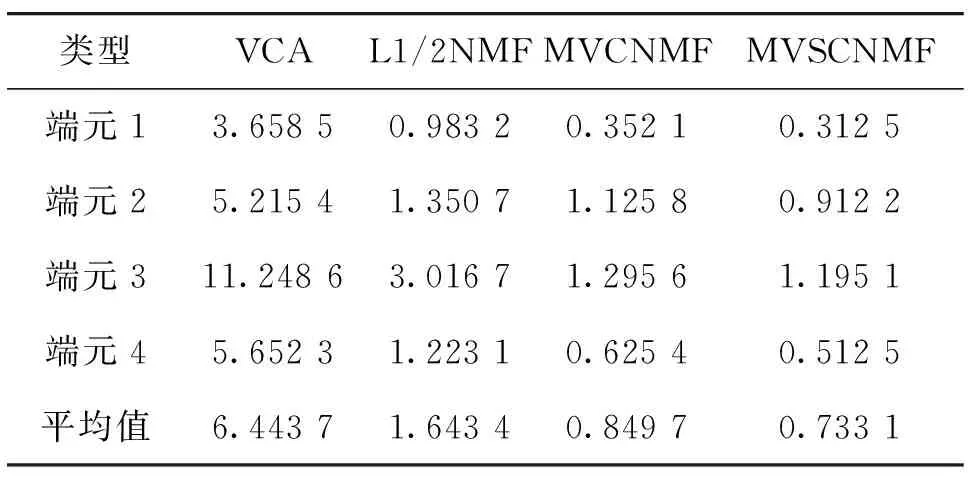
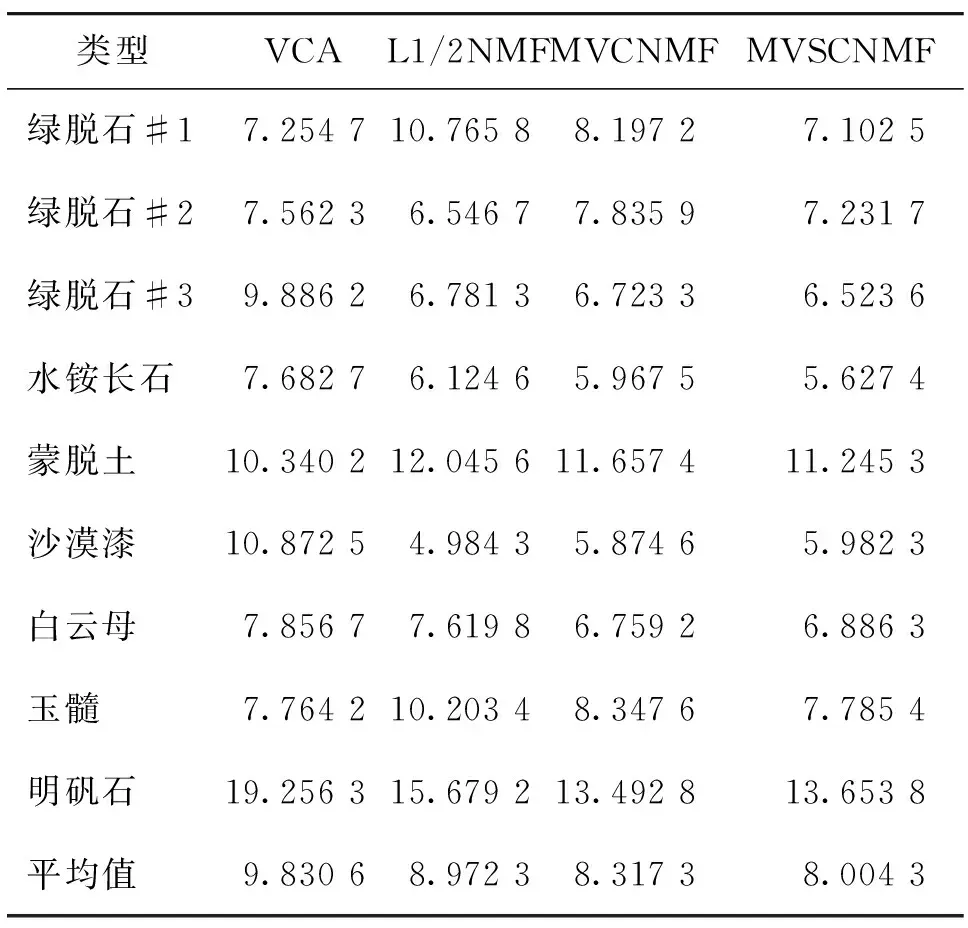
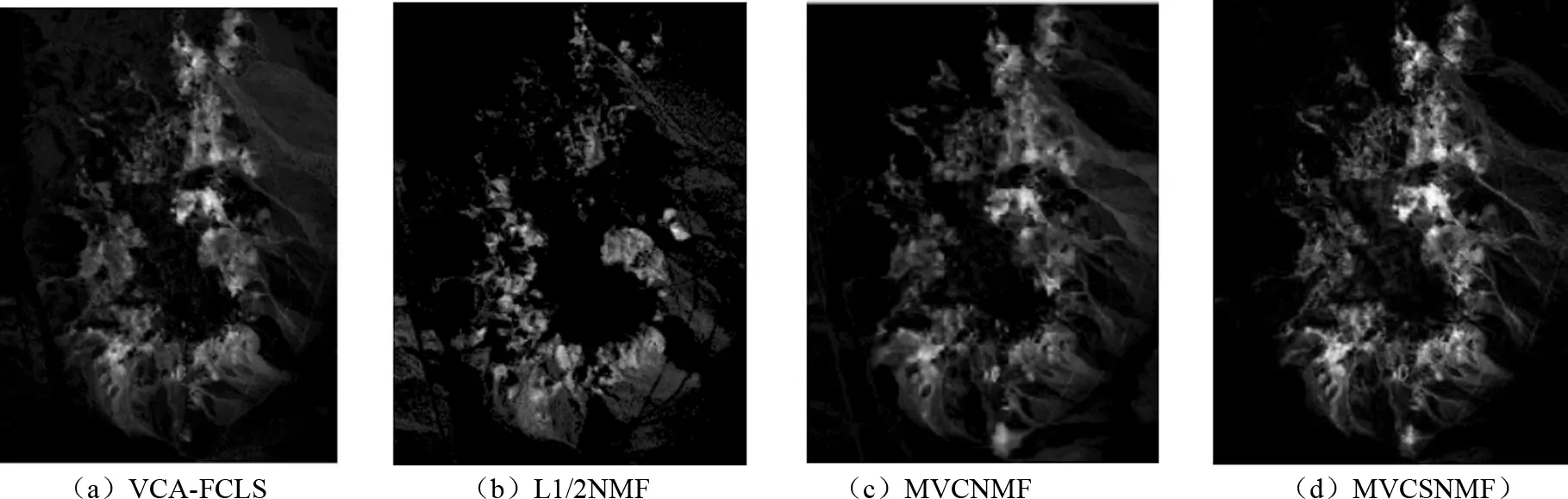
1999年,LEE D和SEUNG S提出了非負(fù)矩陣分解[11]理論。近年來(lái),非負(fù)矩陣分解已成功應(yīng)用到了數(shù)據(jù)降維、文本聚類(lèi)、人臉識(shí)別等領(lǐng)域。對(duì)于非負(fù)矩陣Y∈Rn×m及常數(shù)r Y=WH (2) 使用歐式距離來(lái)定義Y與WH之間的誤差,則目標(biāo)函數(shù)可以表示為 (3) MVCNMF是一種典型的利用端元物理特性在目標(biāo)函數(shù)中添加約束項(xiàng)的方法。該方法通過(guò)將混合像元所構(gòu)成單形體的體積最小化。目標(biāo)函數(shù)定義為: (4) 式中,vol(J(A))表示單形體的體積,由端元矩陣決定。MVCNMF有效地利用了端元矩陣相關(guān)屬性,并對(duì)目標(biāo)函數(shù)進(jìn)行了有效的約束,但是這一方法忽略了豐度的相關(guān)特性。 正如文獻(xiàn)[11]所述,平滑性用來(lái)描述相鄰豐度向量之間的一致性,其也是豐度向量的一種物理屬性。平滑性考慮的是地物本身在空間中分布具有的連續(xù)性,可以使混合像元分解的結(jié)果更加平滑,同時(shí)也可以增加地物在局部空間的主導(dǎo)性。參考文獻(xiàn)[11],平滑性約束項(xiàng)的定義為 (5) (6) 若相鄰像元在數(shù)據(jù)特征空間中越相似,那么該像元間的豐度也就會(huì)越相近。采用文獻(xiàn)[11]中的8領(lǐng)域的結(jié)構(gòu),同時(shí)根據(jù)高斯核函數(shù)計(jì)算ui,j,可得 ui,j=e-‖x(i)-x(j)‖2 (7) 對(duì)公式(5)所述的平滑性約束性求梯度,可得 (8) 式中,S為豐度矩陣,矩陣Q和U定義見(jiàn)公式(6)。 針對(duì)傳統(tǒng)非負(fù)矩陣分解方法分解精度不高等問(wèn)題,本文結(jié)合了最小體積約束和平滑性約束,通過(guò)構(gòu)造最小體積約束和平滑性約束的罰函數(shù)項(xiàng),并將它們同時(shí)添加到了目標(biāo)函數(shù)中,提出了基于最小體積約束和平滑性約束的非負(fù)矩陣分解算法(minimum volume and smooth constrained nonnegative matrix factorization,MVSCNMF)。MVSCNMF的目標(biāo)函數(shù)定義為 (9) 接下來(lái)的問(wèn)題為目標(biāo)函數(shù)的求解,使用交替迭代更新算法來(lái)求解端元矩陣和豐度矩陣,即固定一個(gè)矩陣交替迭代求解另外一個(gè)矩陣,其數(shù)學(xué)模型為 (10) 利用梯度下降法,上述公式可以轉(zhuǎn)換為 (11) MVSCNMF總結(jié)如下: 為了驗(yàn)證本文算法的準(zhǔn)確性和有效性,分別用合成的模擬圖像和真實(shí)的高光譜場(chǎng)景圖像進(jìn)行了實(shí)驗(yàn)。實(shí)驗(yàn)之前,首先提出比較各算法性能的評(píng)價(jià)指標(biāo)。參考文獻(xiàn)[9-10,12-15],采用光譜角距離(spectral angle distance,SAD)來(lái)評(píng)價(jià)分解出的端元和真實(shí)端元之間的相似性。SAD的定義為 (12) 從美國(guó)地質(zhì)勘測(cè)局的光譜資源庫(kù)中隨機(jī)選取了4種端元來(lái)合成模擬的高光譜圖像。所選取的光譜包含了224個(gè)波段,波長(zhǎng)范圍從0.38 μm到2.5 μm。合成的模擬圖像擁有64×64個(gè)像素,然后被分成8×8個(gè)小像素塊,每個(gè)小像素塊都擁有純凈像元。使用一個(gè)7×7的濾波器來(lái)生成模擬的混合像元,為了進(jìn)一步確保模擬圖像中無(wú)純凈像元,對(duì)于那些豐度大于0.8的像素,用上述4種端元均勻構(gòu)成的像元替代。最后,為了模擬可能出現(xiàn)的誤差,通過(guò)向模擬圖像添加信噪比SNR=20 dB的零均值高斯噪音來(lái)實(shí)現(xiàn)。表1列出了新提出的MVSCNMF與其他幾種流行的解混方法的分解效果對(duì)比。 表1 模擬實(shí)驗(yàn)中不同方法下SAD值比較 從表1可以看出,VCA算法在所有的算法中提取端元的效果最差,這是因?yàn)閂CA是從高光譜圖像中提取純凈端元,而模擬圖像中是不存在純凈像元的,所以VCA算法分解效果最差。同時(shí),NMF是一種盲分解算法,不需要原圖像中存在純凈像元,所以基于NMF的算法分解效果比VCA都要好。最后比較MVCNMF、L1/2NMF以及新提出的MVSCNMF發(fā)現(xiàn),新提出的方法分解效果最好。這是因?yàn)?其他方法僅考慮了端元或者豐度的相關(guān)特性,而本文新提出的方法很好地利用了端元和豐度的相關(guān)物理特性,可以明顯地提升混合像元分解的效果。 本文選取了機(jī)載可見(jiàn)光紅外光成像光譜儀獲取的赤銅礦地區(qū)作為真實(shí)的高光譜圖像來(lái)測(cè)試新提出算法的有效性。該高光譜圖像擁有224個(gè)波段,尺寸大小為250×191像素,移除那些被水蒸氣吸收的波段,僅留下其中的188個(gè)波段進(jìn)行實(shí)驗(yàn)。根據(jù)虛擬維度(virtual dimension,VD)算法[16]以及現(xiàn)有的對(duì)該圖像地區(qū)的研究,端元的個(gè)數(shù)設(shè)為9,同時(shí)使用VCA和FCLS算法作為本實(shí)驗(yàn)中端元矩陣A和豐度矩陣S的初始化方法。 上述4種算法關(guān)于提取的端元之間的量化比較DSA值如表2所示。從表2中可以看出,在大部分情況下,NMF的解混結(jié)果比VCA要好。這是因?yàn)樵谠摳吖庾V圖像中是否存在純像元是未知的,所以需要原圖像中存在純凈像元的VCA算法效果最差,而NMF算法不需要原圖像中存在純凈像元,其解混結(jié)果比VCA算法要好。同時(shí)也可以看出,新提出的MVSCNMF算法解混結(jié)果較其他的單一約束的非負(fù)矩陣分解算法(MVCNMF,L1/2NMF)要好。這是因?yàn)镸VCNMF忽略了豐度的平滑性,L1/2NMF則忽略了端元的幾何信息。在NMF的目標(biāo)函數(shù)中,同時(shí)加入體積約束和平滑性約束可以比單約束的NMF帶來(lái)更好的解混效果。本文選取了水銨長(zhǎng)石和白云母兩種地物解混的豐度圖與其他方法進(jìn)行對(duì)比,如圖2、圖3所示。白云母主要分布在圖2左下方三角形區(qū)域以及圖中間偏下的半圓形區(qū)域內(nèi),而水銨長(zhǎng)石主要分布在以圖3各小圖中心為圓心的橢圓形區(qū)域內(nèi)。與真實(shí)分布結(jié)果相比,就白云母的分解結(jié)果來(lái)看,本文的方法較其他方法有效地分解出了左下方三角區(qū)域。就水銨長(zhǎng)石而言,本文的方法較其他方法也能夠很好地剔除圖像四周的非水銨長(zhǎng)石部分。 表2 真實(shí)高光譜圖像實(shí)驗(yàn)中不同方法下DSA值比較 圖2 各算法分解的白云母豐度圖 圖3 各算法分解的水銨長(zhǎng)石豐度圖 本文根據(jù)高光譜圖像的端元和豐度的相關(guān)物理特性,提出了最小體積和平滑性約束的非負(fù)矩陣分解(MVSCNMF)算法。首先,利用端元的幾何特性,將端元構(gòu)成的單形體體積作為約束項(xiàng)添加到了目標(biāo)函數(shù)中。其次,因?yàn)楦吖庾V圖像豐度分布具有平滑性,通過(guò)構(gòu)造豐度的平滑性約束項(xiàng),將其也添加到了目標(biāo)函數(shù)中。最后通過(guò)優(yōu)化求解算法,得到端元矩陣和豐度矩陣。合成的高光譜圖像和真實(shí)的高光譜場(chǎng)景圖像實(shí)驗(yàn)都表明,新提出的方法較原來(lái)的MVCNMF方法及其他流行的混合像元分解算法,解混效果都有了明顯的提升,同時(shí)該方法不需要原始高光譜圖像中存在純凈像元,適用于所有線(xiàn)性混合的高光譜圖像。盡管本文可以提升混合像元分解的精度,但仍存在著矩陣分解迭代求解速度慢,且算法只適用于線(xiàn)性混合像元分解的場(chǎng)景等問(wèn)題。為此,下一步將研究更為有效快速的矩陣求解算法,同時(shí)探索非線(xiàn)性混合模型的混合像元分解方法。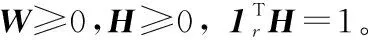
2 最小體積和平滑性約束的非負(fù)矩陣分解
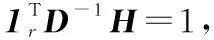
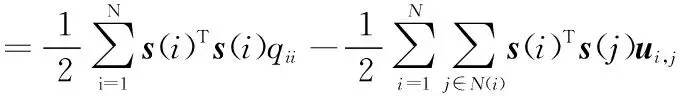
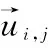
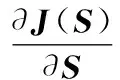
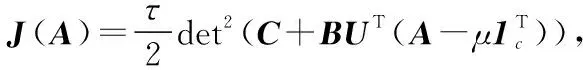
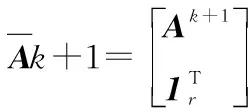
3 實(shí)驗(yàn)
3.1 模擬實(shí)驗(yàn)數(shù)據(jù)
3.2 真實(shí)實(shí)驗(yàn)數(shù)據(jù)

4 結(jié)束語(yǔ)

